1. Introduction

In recent years the development of the calculus in metric spaces has attracted some attention[1-7]. Earlier, F.S. de Blasi, F. Iervolino[8] started the investigation of set differential equations (SDEs) in semilinear metric spaces. This has now evolved into the theory of SDEs as an independent discipline: properties of solutions[1-3,5,36], the impulse equations[1,2,37], control systems[38-41] and asymptotic methods[1-3,42-46]. On the other hand, SDEs are useful in other areas of mathematics. For example, SDEs are used, as an auxiliary tool, to prove existence results for differential inclusions[1,26,31,35]. Also, one can employ SDEs in the investigation of fuzzy differential equations[2,6,21-23, 25,26]. Moreover, SDEs are a natural generalization of the usual ordinary differential equations in finite (or infinite) dimensional Banach spaces.

In many engineering control systems piecewise constant controls, instead of measurable controls are applied. In this article we prove that for any measurable admissible control 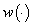and for any 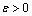there exists piecewise constant admissible control 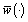such that for set solutions of control set system are 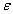-neighbouring.

2. Preliminaries

Let 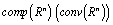be a set of all nonempty (convex) compact subsets from the space,

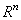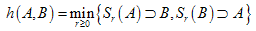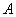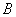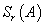be Hausdorff distance between sets and, is 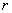-neighborhood of s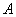et.

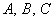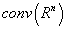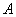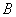Let be in. The set is the Hukuhara difference of and, if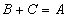, i.e.

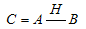From Radstrom's Cancellation Lemma[47], it follows that if this difference exists, then it is unique.

Definition 1[48]. A mapping 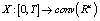is differentiable in the sense of Hukuhara at 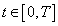if for some 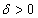the Hukuhara differences

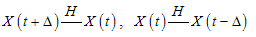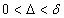exists in for all and there exists an 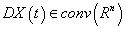such that

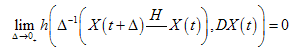and

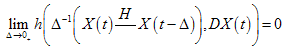Here 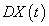is called the Hukuhara derivative of 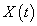at.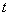

Consider the Cauchy problem with small parameter

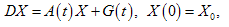(1)

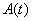where is 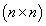-dimensional matrix-valued function; 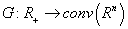is the set-valued map, .

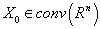Definition mapping 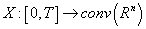is a solution to the problem (1) if and only if it is continuous and satisfies the integral equation

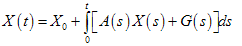for all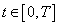. Here the integral is understood in the sense of[48] (the integral exists for example if 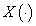is measurable and the real mapping 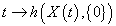is integrable on).

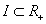Theorem 1[2]. Let the following conditions are true:

1) 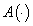is measurable on;

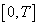2) There exists 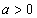such that 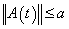for almost every;

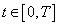3) The set-valued map 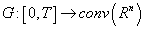is measurable on;

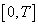4) There exists 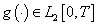such that

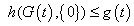almost everywhere on.

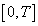Then problem (1) has on 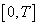exactly one solution.

3. The Control Set Differential Equation

We consider following control set differential equation

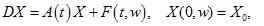(2)

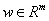where is the control, 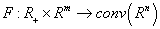is the set-valued map.

Let 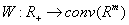be the measurable set-valued map.

Definition 3. The set 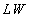of all measurable single-valued branches of the set-valued map 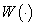is the set of the admissible controls.

Obviously, the control set differential equation (2) turns into the ordinary set differential equation

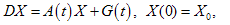(3)

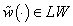if the control is fixed and.

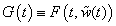Let 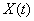denotes the set solution of the differential equation (3), then 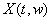denotes the set solution of the control differential equation (2) for the fixed.

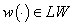Definition 4. The set 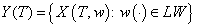be called the attainable set of the system (2).

Theorem 2[49]. Let the following conditions are true:

1) 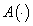is measurable on;

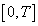2) There exists 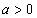such that 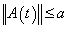for almost every;

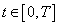3) The set-valued map 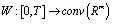is measurable on;

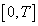4) The set-valued map 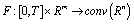satisfies the conditions

a) measurable in;

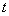b) continuous in;

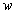5) There exist 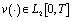and 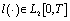such that

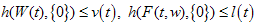almost everywhere on 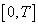and all;

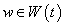6) The set 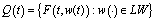is compact and convex for almost every.

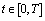Then for every 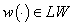there exists the set soluti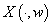on on 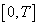and the attainable set 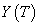is compact and convex.

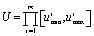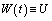Let and on.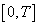

Now, we need to establish that for any measurable admissible control 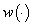and for any 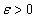there exists piecewise constant admissible control 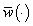such that for set solutions of system (2) holds for all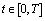

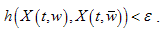Theorem 3. Let the conditions of the theorem 2 are true, and

7) There exists constant 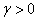such that

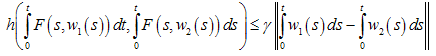for all 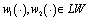and.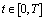

Then for every 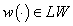there exists 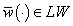such that

1) 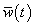is constant on every,;

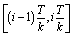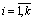2)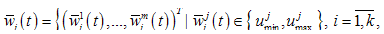

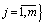for every;

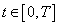3) for all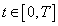

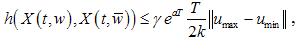where,.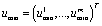

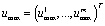Proof. We have any 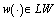and any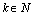. Let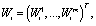

where, ,.

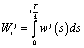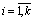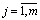Obviously,

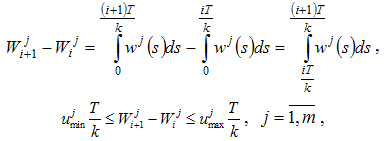and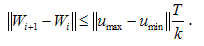

Now we obtain

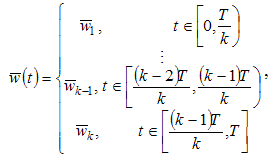such that

1) 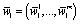, where

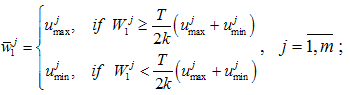2) 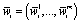, where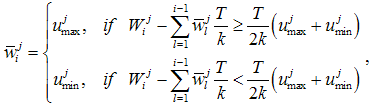

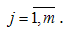Obviously, for 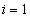and 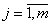we have

a) if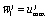, then

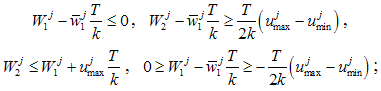b) if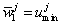, then

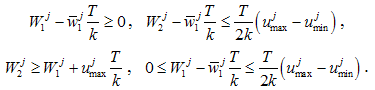Hence we obtain

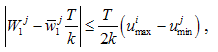and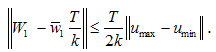

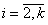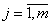
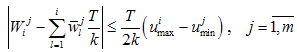Thus, by induction, we obtain that, for and

,and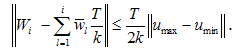

(4)

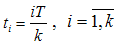Therefore, if; then

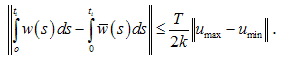Now, we take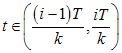. Then

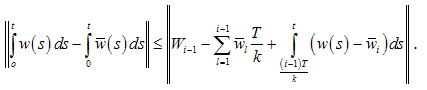As for all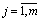

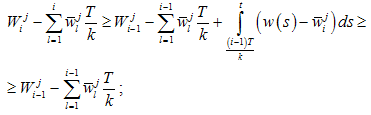then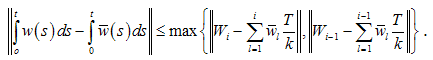

By (4), we get

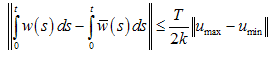(5)

for all.

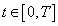Now, applying definition 2 and condition 7 of the theorem, we obtain

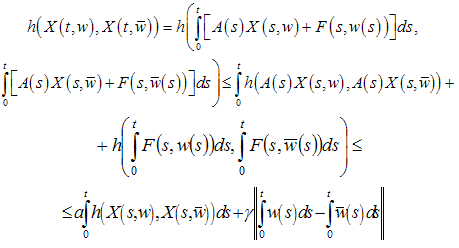Using Gronwall-Bellman's inequality, we obtain

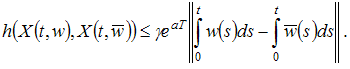By (5), we have

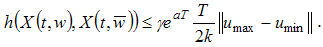Theorem is proved.

Remark. Obviously, if we take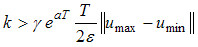; then 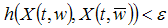for all.

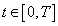4. Conclusions

Here we used the approach of Hukuhara at definition of the derivative which has essential shortages. However the given approach is well investigated by many authors. Also in the literature exist other approaches to definition of the derivative[2,3,9,21,29,36], but also they have the shortages. It is easily possible to show that this outcome will be true for some other cases with little changes.

Also we remark that this result helps to build 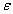-optimal piecewise constant controls for optimal control set system (Mayer problem, time-optimal problem and other).