| [1] | A.M. Wazwaz. (2005) The tanh method: solitons and periodic solutions for the Dodd-Bullough-Tzikhailov and the Tzitzeica-Dodd-Bullough equations, Chaos, Solitons and Fractals, 25, 55-63 |
| [2] | A.M. Wazwaz. (2005) The tanh method and the sine-cosine method for solving the KP-MEW equation, Int. J. Comput. Math., 82 (2) , 235-246 |
| [3] | M.A. Helal, M.S. Mehanna. (2007) The tanh method and Adomian decomposition method for solving the foam drainage equation, Appl. Math. Comput., 190 (1), 599-609 |
| [4] | A.M. Wazwaz. (2007) The extended tanh method for new solitons solutions for many forms of the fifth-order KdV equations, Appl. Math. Comput., 184 (2) 1002-1014 |
| [5] | A.M. Wazwaz. (2007) The extended tanh method for abundant solitary wave solutions of nonlinear wave equations, Appl. Math. Comput., 187, 1131-1142 |
| [6] | A.M. Wazwaz. (2007) New solitons and kinks solutions to the Sharma-Tasso-Olver equation, Appl. Math. Comput., 188 (2), 1205-1213 |
| [7] | A.M. Wazwaz. (2004) A sine-cosine method for handling nonlinear wave equations, Math. Comput. Model., 40, 499-508 |
| [8] | A.M. Wazwaz. (2004) The sine-cosine method for obtaining solutions with compact and noncompact structures, Appl. Math. Comput. , 159 (2), 559-576 |
| [9] | E. Yusufoglu, A. Bekir. (2006) Solitons and periodic solutions of coupled nonlinear evolution equations by using sine-cosine method, Int. J. Comput. Math.., 83(12) ,915-924 |
| [10] | F. Tascan, A. Bekir. (2009) Analytic solutions of the (2 + 1)-dimensional nonlinear evolution equations using the sine-cosine method, Appl. Math. Comput., 215, 3134-3139 |
| [11] | Z. Xiqiang, W. Limin, S. Weijun. (2006) The repeated homogeneous balance method and its applications to nonlinear partial differential equations, Chaos, Solitons and Fractals, 28(2), 448-453 |
| [12] | S.J. Liao, Beyond Perturbation: Introduction to the homotopy analysis method, Chapman & Hall/CRC Press, Boca Raton, 2003 |
| [13] | S.J. Liao. (2004) On the homotopy analysis method for nonlinear problems, Appl. Math. Comput.., 147, 499-513 |
| [14] | S.J. Liao. (2005) A new branch of solutions of boundary-layer flows over an impermeable stretched plate, Int. J. Heat Mass Transfer, 48, 2529-2539 |
| [15] | S.J. Liao. (2009) A general approach to get series solution of non-similarity boundary-layer flows, Commun. Nonlinear Sci. Numer. Simul., 14(5), 2144-2159 |
| [16] | M.T. Darvishi, F. Khani. (2009) A series solution of the foam drainage equation, Comput. Math. Appl., 58, 360-368 |
| [17] | A. Aziz, F. Khani, M.T. Darvishi. (2010) Homotopy analysis method for variable thermal conductivity heat flux gage with edge contact resistance, Zeitschrift fuer Naturforschung A, 65a(10) , 771-776 |
| [18] | F. Khani, M.T. Darvishi, R.S.R. Gorla. (2011) Analytical investigation for cooling turbine disks with a non-Newtonian viscoelastic fluid, Comput. Math. Appl., 61(7), 1728-1738 |
| [19] | E. Fan, Z. Jian. (2002) Applications of the Jacobi elliptic function method to special-type nonlinear equations, Phys. Lett. A., 305 (6), 383-392 |
| [20] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2010) Exact three-wave solutions for high nonlinear form of Benjamin-Bona-Mahony-Burgers equations, International Journal of Mathematical and Computer Sciences, 6(3), 127-131 |
| [21] | M.T. Darvishi, Mohammad Najafi. (2012) Some exact solutions of the (2+1)-dimensional breaking soliton equation using the three-wave method, World Academy of Science, Engineering and Technology, 87, 31-34 |
| [22] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2010) New exact solutions for the (3+1)-dimensional breaking soliton equation, International Journal of Information and Mathematical Sciences, 6(2), 134-137 |
| [23] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2010) New application of EHTA for the generalized (2+1) -dimensional nonlinear evolution equations, International Journal of Mathematical and Computer Sciences, 6(3), 132-138 |
| [24] | M.T. Darvishi, Mohammad Najafi. (2011) A modification of extended homoclinic test approach to solve the (3+1)- dimensional potential-YTSF equation, Chin. Phys. Lett., 28(4), art. no. 040202 |
| [25] | M.T. Darvishi, Mohammad Najafi. (2012) Some complexiton type solutions of the (3+1)-dimensional Jimbo-Miwa equation, World Academy of Science, Engineering and Technology, 87, 42-44 |
| [26] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2012) Traveling wave solutions for the (3+1)-dimensional breaking soliton equation by (G’/G)-expansion method and modified F-expansion method, World Academy of Science, Engineering and Technology, 88, 37-42 |
| [27] | J.H. He, M.A. Abdou. (2007) New periodic solutions for nonlinear evolution equations using Exp-function method, Chaos, Solitons and Fractals, 34, 1421-1429 |
| [28] | F. Khani, S. Hamedi-Nezhad, M.T. Darvishi, S.-W. Ryu (2009) New solitary wave and periodic solutions of the foam drainage equation using the Exp-function method, Nonlin. Anal.: Real World Appl., 10, 1904-1911 |
| [29] | B.C. Shin, M.T. Darvishi, A. Barati. (2009) Some exact and new solutions of the Nizhnik-Novikov-Vesselov equation using the Exp-function method, Comput. Math. Appl., 58(11/12) , 2147-2151 |
| [30] | X.H. Wu, J.H. He. (2008) Exp-function method and its application to nonlinear equations, Chaos, Solitons and Fractals, 38(3), 903-910 |
| [31] | A. Biswas. (2010) A Topological 1-soliton solution of Kadomtsev-Petviashvili equation with power law nonlinearity, Appl. Math. Comput., 217, 1771-1773 |
| [32] | A. R. Adem, C. M. Khalique, A. Biswas. (2011) Solutions of Kadomtsev–Petviashvili equation with power law nonlinearity in (1+3) dimensions, Math. Meth. Appl. Sci., 34 532-543 |

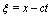 into the PDE
into the PDE 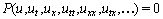
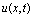 is traveling wave solution. This enables usto use the following changes:
is traveling wave solution. This enables usto use the following changes: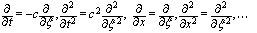
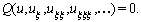
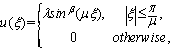
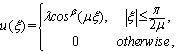
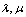 and
and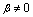 are parameters that will be determined,
are parameters that will be determined, 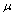 and
and 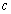 are the wave number and the wave speed respectively. We use
are the wave number and the wave speed respectively. We use 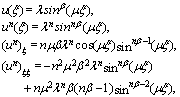
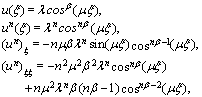
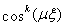 or
or 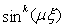 and set to zero their coefficients to get a system of algebraic equations among the unknowns
and set to zero their coefficients to get a system of algebraic equations among the unknowns 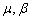 and
and 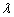 . We obtained all possible value of the parameters
. We obtained all possible value of the parameters 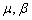 and
and 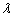 [7].
[7]. 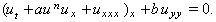
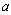 and
and 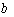 are real valued constants. After that we use the transformation
are real valued constants. After that we use the transformation 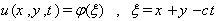
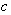 is constant. There for the Eq. (8) converts to
is constant. There for the Eq. (8) converts to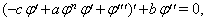
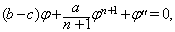
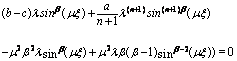
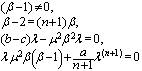
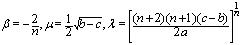
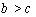 , the following periodic solutions
, the following periodic solutions 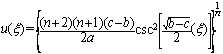
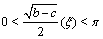 , and
, and 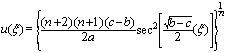
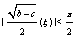 .However, for
.However, for 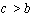 , the following periodic solutions
, the following periodic solutions 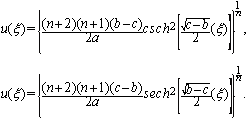
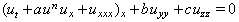
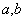 and
and 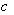 are real valued constants. After that we use the transformation
are real valued constants. After that we use the transformation 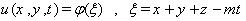
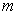 is constant. There for the Eq. (17) converts to
is constant. There for the Eq. (17) converts to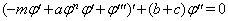
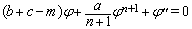
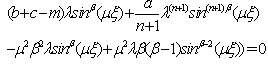
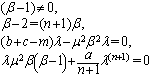
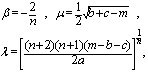
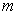 is a free parameter. Hence, for
is a free parameter. Hence, for 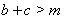 , the following periodic solutions
, the following periodic solutions 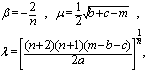
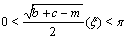 , and
, and 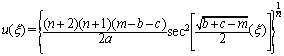
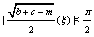 .However, for
.However, for 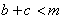 , the following periodic solutions
, the following periodic solutions 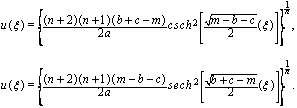
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML