1. Introduction

Structures may experience blast loads due to military actions, accidental explosions or terrorist activities. Such loads may cause severe damage or collapse due to their high intensity, dynamic nature, and usually different direction compared to common design loads. The occurrence of plate structure is extensive in various engineering constructions. Nonlinear vibration occurs very often in many applications of panels, particularly in aircraft. Aircraft skin – panels especially those near the exhaust of jet engines, are often subject to high levels of acoustic pressure. This may result in large amplitude, nonlinear vibration of panels. Extensive literature reviews on the nonlinear vibration of plates subjected to different loading are given by the following researchers. Rao et al (1993) presented a finite element method for the large amplitude free flexural vibration of unstifened and stiffened plates. For the simply supported square plate, non-linear frequency ratios from six different approaches were reported. The frequency ratio at 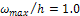varied from a low of 1.2967 to a high of 1.5314. Chiang et al. (1991) developed a rectangular element with 24 degrees of freedom (6 DOF per node). The linearized updated-mode was used to study the harmonic forced vibration. Although the in-plane displacements were included in the formulation, only bilinear functions were employed for the in-plane displacement shape functions. Rao, S. R. A. et al (1992) use finite elementmethod to study large – amplitude free flexural vibration of stiffened and unstiffened plates. They employed the total Lagrangian coordinates system to formulate the dynamic version of Von Karman's field equations where the stiffener has been elegantly modeled so that it may lie anywhere within the plate element. Chorng-Fuh L. and Ge-Tzung C. (1995) present a simple finite element analysis of axisymmetric vibration of annular and circular plates. They based the formulation of the finite element on elasticity theory which has no assumptions as in the conventional plate theory-based analysis. They show that different simply supported conditions can make significant differences in the prediction of axisymmetric vibration frequencies for both thin and thick plates. Ding H. et al (1999) experimentally studied free axisymmetric vibration of transversely isotropic piezoelectric circular plates. They used Finite Hankel transforms and the boundary variables in free terms are replaced for two kinds of boundary conditions to obtain ordinary differential equations with constant coefficients to derive axisymmetric state space for mulation of piezoelectric laminated circular plates. They found that exact solutions can be obtained for two kinds of boundary conditions and the solutions can be used to examine the validity of various plate theories and numerical calculation software. Aiyesimi, Y. M. (1999) investigates the dynamic analysis of an elastic plate with point-moving load. He determine Mathematically the vibrating conditions that give rise to the occurrence of natural frequency and the moving load constitute an external vibration. Aiyesimi, Y. M. (2000) studied the analytical investigation of the effect of amplitude ratio on the dynamic response of a viscoelastic plate subject to a cyclic moving load. The vibrating plate is incorporated with a damping foundation regarded as a viscoelastic foundation where he analyzed the effect of the amplitude ratio on the magnitude of the vibration and observed that the amplitude of vibration increases with the amplitude ratio. Amabili, M. et al (2003) experimentally studied large amplitude vibrations of a stainless – steel circular cylindrical panel supported at four edges. The nonlinear response to harmonic excitation of different magnitudes in the neighborhood of three resonances was investigated. Experiments showed that the curved panel exhibited a relatively strong geometric nonlinearly of softening type. Sathyamoorthy, M. (1996) studied the influence of transverse shear and rotatory inertia on non-linear vibration of circular plates. Effects of transverse shear deformation and rotatory inertia have been included in the Berger - type governing equations. He found that the present Berger - type formulation in the polar coordinate system is found to yield reasonable good results for plates with immovable boundary conditions. Ming-Hui, L. and Tsung-Chien, C. (2008) used inverse method to investigate blast load input estimation of the medium girder bridge. An adaptive weighted input estimation inverse methodology is applied to estimate the unknown time-varying blast loads in a truss structural system. The FEM is adopted to construct the state equation of the truss structure, and the Kalman filter is further combined with the adaptive weighted recursive least square estimator, which recursively estimates the unknown blast loads under a situation that the system involves the measurement and modeling errors. Their results indicate that the presented technique will have higher estimation ability adopting the precise measurement instrument. Van der Meer, L. J (2008) experiment the dynamic response of high-rise building structures to blast loading. The SDOF response is determined analytically for linear-elastic material behavior, idealized blast loads and without damping. The response is divided in three regimes: impulsive, dynamic and quasi-static. He concluded that the SDOF system is not conservative for response in the impulsive regime, whereas the quasi-static response is similar for both models. BLEVE (boiling liquid expanding vapor explosion) blast loading on high-rise buildings is likely in the impulsive regime. Olarewaju, A. J. et al (2011) Simulated and Verified the blast load duration for studying the response of underground horizontal and vertical pipes using finite element method. They used time integration technique in Abaqus/Explicit to solve the equation of motion. From their result of the response of underground pipes due to surface blast, for various periods considered, it was observed that duration of blast play a significant role in the response of pipes buried, most especially pipes buried in dense sand and undrained clay.

2. Exponential Blast

An actual bomb explosion, like most blast loads, has a random pressure – time history. However, such an explosion invariably has a sharp pressure rise followed by a time of decay. The pulse shapes shown in figure 1. is the exponential blast wave

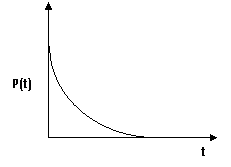Figure 1. Exponential decay

The modified Friedlander exponential decay equation.

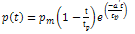(2.1)

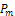where is the initial pressure, 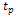is the time of reversal of direction of pressure, and 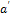is a shape parameter depending on the dimensionless scaled distance given by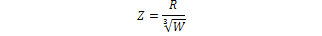

in which R is the distance from the centre of a spherical shape in meters and W is the charge mass expressed in kilograms.

3. Mathematical Model for Circular Plate

We consider a circular plate subject to a uniformly distributed impulsive load I of radius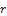, thickness 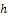and clamped at the edges.

Figure 2. A schematic diagram of the clamped circular solid plate under the blast loading

3.1. Governing Equation of Motion for a Circular Plate

The governing equation of motion for the damped vibration of circular plate under blast loading[22] is given as

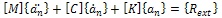(3.1)

where [K], the stiffness matrix is given as

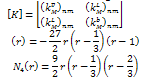(3.2)

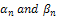Similarly, the displacement components at any point within the element arewhere at a node n, u_n, v_n, w_n are the translational displacements and are the slop functions.

In the case of axisymmetric deformation where the integrand is independent of the tangential coordinate [22].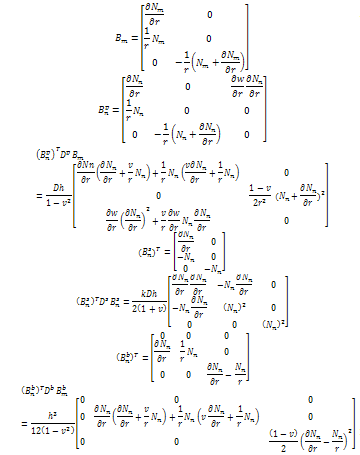

Since the plate is clamped, we have

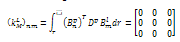Applying the interpolation functions, we have the material part of the stiffness matrix to be

(3.4)

The mass matrix [M] is obtain from the kinetic energy of the circular plate element

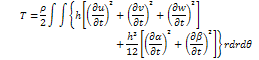Applying the displacement components, we have

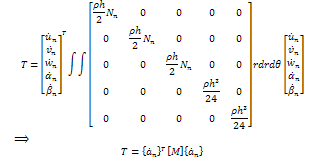where [M] the mass matrix is

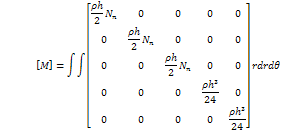With interpolation functions and applying the axisymmetric deformation, we have

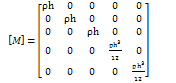(3.5)

The damping matrix [C] is formed as a linear combination of the stiffness and mass matrices; i.e.,

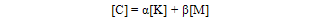where α and β are called the proportional damping constants.

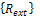is the external load, in this case an exponential blast loading.

The elements equation of motion are

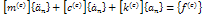(3.6)

For free vibration response [10], equation (3.6) reduces to

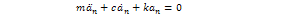In the case of under damped, the solution to the above equation is

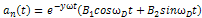(3.7)

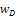where is the damped natural circular frequency, given by

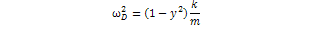and,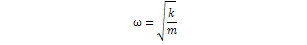

B₁ and B₂ are constants to be determined using the given boundary conditions.

Solution of forced vibration 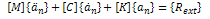(3.8)

Applying the transformation using the normalized matrix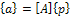, equation (3.8) becomes 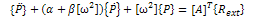(3.9)

where 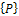is the column matrix of generalized displacements, which are linear combinations of the actual modal displacements 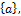and 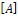is the normalized modal matrix.

and

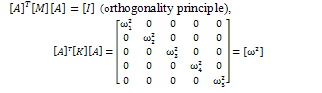Solving the decoupled equation

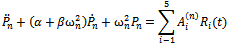(3.10)

We consider one of the terms of the right hand side of equation (3.10) subject to a uniform blast described by the modified Friedlander exponential decay equation.

Equation (3.10) now becomes

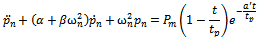(3.11)

Equation (3.11) has the solution

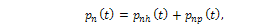where the homogenous solution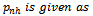

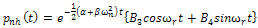with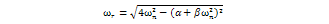

To obtain the particular integral , we then assume a solution of the form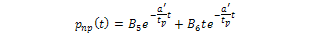

On substitution, we have

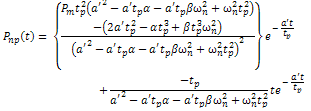Gives the general solution

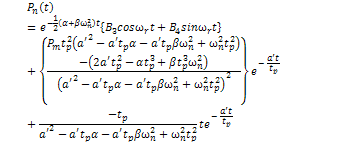To obtain the actual displacement, we apply the transformation matrix

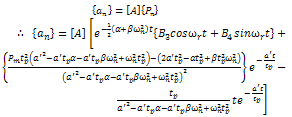(3.12)

with the initial conditions

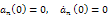
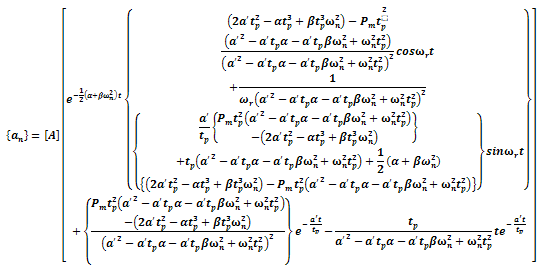
4. Numerical Experimentation

We employ the MAPLE 12 Mathematical Computer Software to solve the system stiffness matrix [K], the system mass matrix [M], the fundamental frequency ω, and the system force matrix [P]. The displacement profiles of the circular plate are displayed.

The material employed is the clamped circular plate, with the following dimensions and mechanical properties.

Radius r = 2 m

Thickness h = 0.003 m

Density

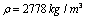Young’s modulus

Poisson’s ratio

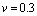The external load material properties are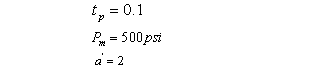

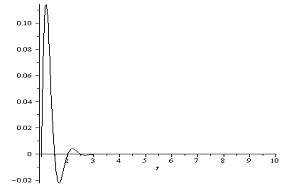Figure 5. Vibration of Damped Circular Plate subject to Exponential Blast pulse,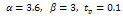

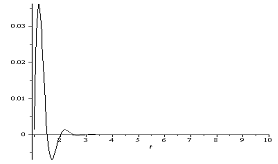Figure 6. Vibration of Damped Circular Plate subject to Exponential Blast pulse,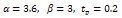

5. Discussion of Results

Dynamic analyses of damped circular plate with shear deformation and rotator inertia subject to blast loading were considered. Equation (3.13) gives the dynamic response damped circular plate subjected to exponential blast loading. In fig 4.1. and fig 4.2, the effect on exponential blast loading to clamped circular plate with two different values of pulse duration (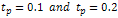) are reported. While the lowest pulse duration gives rises to the vibration amplitude, the effect on damping dies out the amplitude quickly.

ACKNOWLEDGEMENTS

We would like to sincerely and wholeheartedly thank the management and the entire staff of my institution Federal University of Technology, Minna for given us enabling environment to carry out this research work.