Rajan Arora, Mohd. Junaid Siddiqui, V. P. Singh
DPT, IIT Roorkee, Saharanpur Campus, Saharanpur, UP-247001, India
Correspondence to: Rajan Arora, DPT, IIT Roorkee, Saharanpur Campus, Saharanpur, UP-247001, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The modified equal width equation and its variant are investigated. We have presented a Reduced differential transform method to solve the MEW equation, its variant and non-homogeneous Burgers’ equation. This method is an alternative approach to overcome the demerit of complex calculation of differential transform method, capable of reducing the size of calculation and easily overcoming the difficulty of the perturbation technique or Adomain polynomials.The approximate analytical solutions of the equations are calculated in the form of series with easily computable components. Numerical results are derived and the obtained results are found in good agreement with the exact solutions.
Keywords:
Reduced Differential Transform Method (RDTM), Modified Equal Width (MEW) Equation And Its Variant, Non-Homogeneous Burgers’ Equation, Approximate Solution, Analytical Solution
Cite this paper: Rajan Arora, Mohd. Junaid Siddiqui, V. P. Singh, Solution of the Modified Equal Width Equation, its Variant and non-homogeneous Burgers’ equation by RDT Method, American Journal of Computational and Applied Mathematics , Vol. 1 No. 2, 2011, pp. 53-56. doi: 10.5923/j.ajcam.20110102.10.
1. Introduction
Nonlinear wave phenomena plays a major role in sciences such as fluid mechanics, plasma physics, solid state physics, optical fibers, chemical kinetics and geochemistry. The phenomena of dispersion, dissipation, diffusion, reaction and convection are very important in nonlinear wave equations[1]. Because of the complexity of the nonlinear wave equations, there is no unified method to find the solutions of these equations. Several methods, analytical and numerical, such as the homogeneous balance method[2], Hirota bilinear method[3], Variational iteration method[4], the decomposition method[5], Backlund transformation and inverse scattering method[6], Homotopy Perturbation method[7], the sine–cosine methods[8], the Tan hyperbolic function method[9] and the Reduced Differential transform method[10] are used to solve the partial differential equations governing the nonlinear waves. The MEW equation, which is related to the RLW equation, has solitary wave solutions with both positive and negative amplitudes, all of which have the same width[11,12]. The MEW equation is a nonlinear wave equation with cubic nonlinearity with a pulse like solitary wave solution. The present work is motivated by the intention to extend the use of earlier method in the literature to solve the MEW equation, its nonlinear variant and the non-homogeneous Burgers’ equation. In this paper, we solve the above problems by the Reduced Differential transform method[10]. The main advantage of the method is the fact that it provides its user with an analytical approximation, in many cases an exact solution, in a rapidly convergent sequence with elegantly computed terms. The structure of this paper is organized as follows:In section 2, we begin with some basic definitions and explain the Reduced differential transformation method. In section 3, we apply this method to solve the above three problems.
2. Analysis of the method
The basic definitions in the Reduced Differential transform method[10] are as follows:
2.1. Definition
If function u(x; t) is analytic and k-times continuously differentiable withrespect to time t and space x in the domain of interest, then let 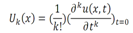 | (1) |
where the function 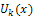 is the transformed function of the original function
is the transformed function of the original function 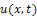 . The differential inverse transform of
. The differential inverse transform of 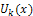 is defined as follows
is defined as follows 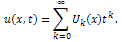 | (2) |
Then combining these two equations we write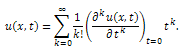 | (3) |
From the above definitions, it can be found that the concept of the Reduced Differential transform method is derived from the Taylor’s series expansion.We write the gas dynamics equation in standard form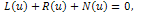 | (4) |
with initial condition 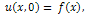 | (5) |
where 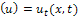 ,
, 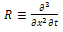 is a linear operator which has mixed partial derivatives and
is a linear operator which has mixed partial derivatives and 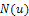 is a nonlinear term. According to RDTM, the iteration formula is
is a nonlinear term. According to RDTM, the iteration formula is 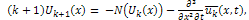 | (6) |
where 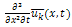 and
and 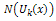 are the reduced differential transform transformations of the functions
are the reduced differential transform transformations of the functions 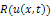 and
and 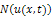 , respectively.Definition 2.1 implies that the initial approximation
, respectively.Definition 2.1 implies that the initial approximation 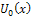 is given by the initial condition, that is
is given by the initial condition, that is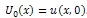 | (7) |
Substituting 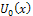 in the iteration formula (6), we obtain the values of
in the iteration formula (6), we obtain the values of 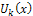 . Then the differential inverse transformation of the set of values
. Then the differential inverse transformation of the set of values 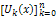 gives approximation solution as
gives approximation solution as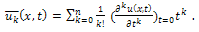 | (8) |
3. Applications
Now, we will solve three problems using the RDTM.
3.1. The Modified Equal width (MEW) Equation
The modified equal width (MEW) equation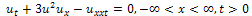 | (9) |
has been discussed in[11,12]. Here 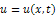 is its solution.The MEW equation, which is related to the RLW equation, has solitary waves solutions with both positive and negative amplitudes, all of which have the same width. The MEW equation is a nonlinear wave equation with cubic nonlinearity with a pulse like solitary wave solution.We consider above equation with the initial condition
is its solution.The MEW equation, which is related to the RLW equation, has solitary waves solutions with both positive and negative amplitudes, all of which have the same width. The MEW equation is a nonlinear wave equation with cubic nonlinearity with a pulse like solitary wave solution.We consider above equation with the initial condition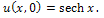 | (10) |
We know that the exact solution for above problem is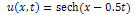 | (11) |
By RDTM, the transformed form of equation (9) is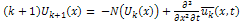 | (12) |
where 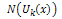 is the Reduced Differential transformation of
is the Reduced Differential transformation of 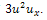 Using the initial condition (11), we obtain
Using the initial condition (11), we obtain 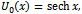
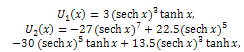 and so on.Then, the differential inverse transformation of the set of values
and so on.Then, the differential inverse transformation of the set of values 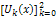 gives the second order approximation solution as
gives the second order approximation solution as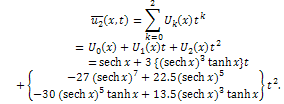 Therefore, the exact solution of (9) with the initial condition (10) is given by
Therefore, the exact solution of (9) with the initial condition (10) is given by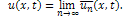 The comparison of the present approximation solutions with the exact solutions of the MEW equation is made in the following table:
The comparison of the present approximation solutions with the exact solutions of the MEW equation is made in the following table:Table 1. Comparison of the approximate solutions with the exact solutions of MEW equation (9) with initial condition (10)
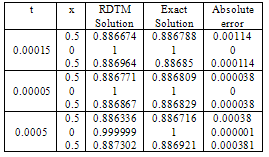 |
| |
|
3.2. The Variant of Modified Equal width (MEW) Equation
Consider the variant of modified equal width (MEW) equation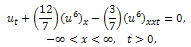 | (13) |
with the initial condition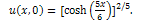 | (14) |
Here 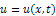 .We know that the exact solution for above problem is
.We know that the exact solution for above problem is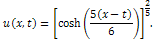 | (15) |
By RDTM, the transformed form of equation (13) is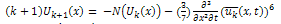 | (16) |
where 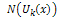 is the Reduced Differential transformation of
is the Reduced Differential transformation of 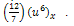 Using the initial condition (14), we obtain
Using the initial condition (14), we obtain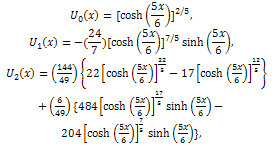 and so on.Then, the differential inverse transformation of the set of values
and so on.Then, the differential inverse transformation of the set of values 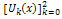 gives the second order approximation solution as
gives the second order approximation solution as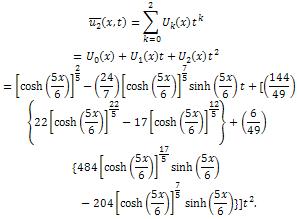 Therefore, the exact solution of (13) with the initial condition (14) is given by
Therefore, the exact solution of (13) with the initial condition (14) is given by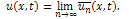 The comparison of the present approximation solutions with the exact solutions of the variant of MEW equation is made in the following table:
The comparison of the present approximation solutions with the exact solutions of the variant of MEW equation is made in the following table:Table 2. Comparison of the approximate solution with the exact solution of the equation (13) with initial condition (14)
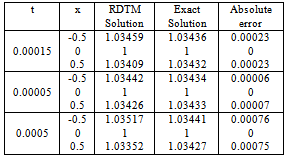 |
| |
|
3.3. Burgers’ equation
Consider the non-homogeneous Burgers’ equation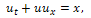 | (17) |
with the initial condition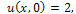 | (18) |
with 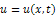 is its solution.Taking Reduced Differential transform of equation (17), we obtain
is its solution.Taking Reduced Differential transform of equation (17), we obtain 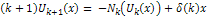 | (19) |
where 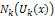 is the Reduced Differential transformation of
is the Reduced Differential transformation of 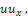 and
and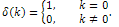 Using the initial condition (18), we obtain the initial approximation as
Using the initial condition (18), we obtain the initial approximation as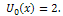 Using the definition of RDTM, first few terms
Using the definition of RDTM, first few terms 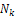 and
and 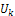 are as follows
are as follows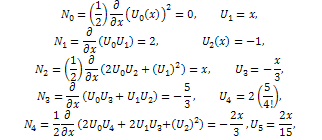 and so on.Then, the differential inverse transformation of the set of values
and so on.Then, the differential inverse transformation of the set of values 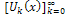 gives the solution as
gives the solution as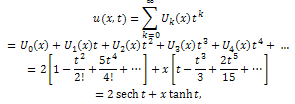 which is an exact solution of the equation (17) with initial condition (18).
which is an exact solution of the equation (17) with initial condition (18).
4. Conclusions
The main goal of the present work is to implement the Reduced Differential transform method[10], and more importantly to overcome the computational difficulty of Differential Transform method. The aims of this work were achieved, and travelling wave solutions were formally obtained as a power series. The transformation technique was used to demonstrate that our analysis is applicable to a variety of nonlinear evolution equations.The main advantage of the method is the fact that it provides its user with an analytical approximation, in many cases an exact solution, in a rapidly convergent sequence with elegantly computed terms. Its small size of computation in comparison with the computational size required in other numerical methods, and its rapid convergence show that the method is reliable and introduces a significant improvement in solving the MEW equation and Burgers’ equation over existing methods. As the method is usually tedious, we have used the software package “Mathematica” to calculate the series obtained from the RDTM.
ACKNOWLEDGEMENTS
Research fundings from the Department of Science and Technology (DST), Government of India, New Delhi, vide sanction order no. SR/FTP/MS-12/2008 and from the CSIR, New Delhi vide reference number 09/143 (0765)/2010-EMR-I are gratefully acknowledged.
References
| [1] | G. B. Whitham, Linear and Non Linear Waves, Wiley-Interscience, New York, 1974 |
| [2] | M. Wang, Y. Zhou and Z. Li, Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics, Physics Letters A, 216, 67–75, 1996 |
| [3] | X.-B. Hu and Y.-T. Wu, Application of the Hirota bilinear formalism to a new integrable differential- difference equation, Physics Letters A, 246 (6), 523–529, 1998 |
| [4] | J. H. He, Variational iteration method-a kind of non-linear analytical technique: Some examples, International Journal of Non-Linear Mechanics, 34(4), 699-708, 1999 |
| [5] | D.J. Evans and H. Bulut, A new approach to the gas dynamics equation, an application of the decomposition method, International Journal of Computer Mathematics, 79(7), 817-822, 2002 |
| [6] | V.O. Vakhnenko, E.J. Parkes and A.J. Morrison, A Bäcklund transformation and the inverse scattering transform method for the generalized Vakhnenko equation, Chaos Solitons Fractals, 17 (4), 683–692, 2003 |
| [7] | J. H. He, Homotopy Perturbation method: A new nonlinear technique, Applied Mathematics and computation, 135, 73-79, 2003 |
| [8] | A.M. Wazwaz, A Sine-Cosine method for handling Nonlinear Wave Equations, Mathematical and Computer modelling, 40, 499-508, 2004 |
| [9] | A.M. Wazwaz, Handbook of Differential Equations: Evolutionary Equations 4, Elsevier, 485-568, 2008 |
| [10] | Y. Keskin and G. Oturanc, Reduced Differential Transform Method for Partial Differential equations, International Journal of Nonlinear Sciences and Numerical Simulation, 10(6), 741-749, 2009 |
| [11] | P.J. Morrison, J.D. Meiss and J.R. Cary, Scattering of RLW Solitary waves, Physica D: Non-linear Phenomena, 11, 324-336, 1984 |
| [12] | L.R.T. Gardner and G. A. Gardner, Solitary waves of the equal width wave equation, Journal of Computational Physics, 101, 218-223, 1992 |

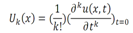
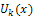 is the transformed function of the original function
is the transformed function of the original function 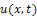 . The differential inverse transform of
. The differential inverse transform of 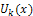 is defined as follows
is defined as follows 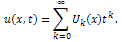
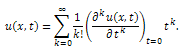
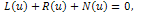
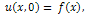
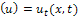 ,
, 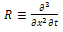 is a linear operator which has mixed partial derivatives and
is a linear operator which has mixed partial derivatives and 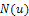 is a nonlinear term. According to RDTM, the iteration formula is
is a nonlinear term. According to RDTM, the iteration formula is 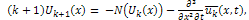
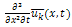 and
and 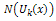 are the reduced differential transform transformations of the functions
are the reduced differential transform transformations of the functions 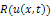 and
and 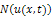 , respectively.Definition 2.1 implies that the initial approximation
, respectively.Definition 2.1 implies that the initial approximation 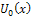 is given by the initial condition, that is
is given by the initial condition, that is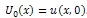
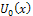 in the iteration formula (6), we obtain the values of
in the iteration formula (6), we obtain the values of 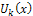 . Then the differential inverse transformation of the set of values
. Then the differential inverse transformation of the set of values 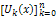 gives approximation solution as
gives approximation solution as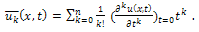
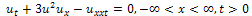
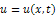 is its solution.The MEW equation, which is related to the RLW equation, has solitary waves solutions with both positive and negative amplitudes, all of which have the same width. The MEW equation is a nonlinear wave equation with cubic nonlinearity with a pulse like solitary wave solution.We consider above equation with the initial condition
is its solution.The MEW equation, which is related to the RLW equation, has solitary waves solutions with both positive and negative amplitudes, all of which have the same width. The MEW equation is a nonlinear wave equation with cubic nonlinearity with a pulse like solitary wave solution.We consider above equation with the initial condition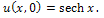
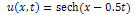
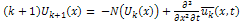
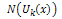 is the Reduced Differential transformation of
is the Reduced Differential transformation of 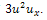 Using the initial condition (11), we obtain
Using the initial condition (11), we obtain 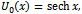
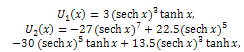 and so on.Then, the differential inverse transformation of the set of values
and so on.Then, the differential inverse transformation of the set of values 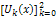 gives the second order approximation solution as
gives the second order approximation solution as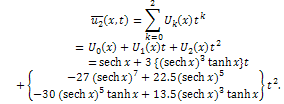 Therefore, the exact solution of (9) with the initial condition (10) is given by
Therefore, the exact solution of (9) with the initial condition (10) is given by The comparison of the present approximation solutions with the exact solutions of the MEW equation is made in the following table:
The comparison of the present approximation solutions with the exact solutions of the MEW equation is made in the following table:
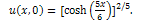
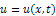 .We know that the exact solution for above problem is
.We know that the exact solution for above problem is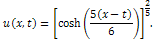
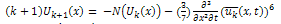
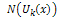 is the Reduced Differential transformation of
is the Reduced Differential transformation of 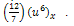 Using the initial condition (14), we obtain
Using the initial condition (14), we obtain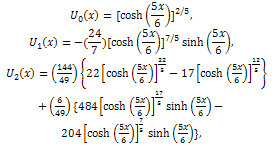 and so on.Then, the differential inverse transformation of the set of values
and so on.Then, the differential inverse transformation of the set of values 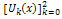 gives the second order approximation solution as
gives the second order approximation solution as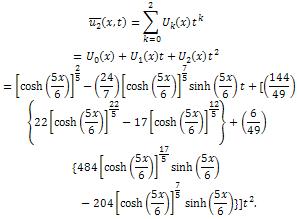 Therefore, the exact solution of (13) with the initial condition (14) is given by
Therefore, the exact solution of (13) with the initial condition (14) is given by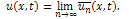 The comparison of the present approximation solutions with the exact solutions of the variant of MEW equation is made in the following table:
The comparison of the present approximation solutions with the exact solutions of the variant of MEW equation is made in the following table: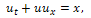
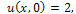
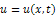 is its solution.Taking Reduced Differential transform of equation (17), we obtain
is its solution.Taking Reduced Differential transform of equation (17), we obtain 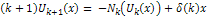
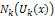 is the Reduced Differential transformation of
is the Reduced Differential transformation of 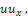 and
and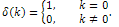 Using the initial condition (18), we obtain the initial approximation as
Using the initial condition (18), we obtain the initial approximation as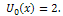 Using the definition of RDTM, first few terms
Using the definition of RDTM, first few terms 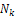 and
and 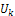 are as follows
are as follows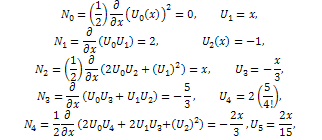 and so on.Then, the differential inverse transformation of the set of values
and so on.Then, the differential inverse transformation of the set of values 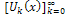 gives the solution as
gives the solution as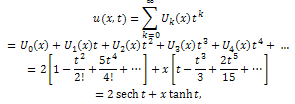 which is an exact solution of the equation (17) with initial condition (18).
which is an exact solution of the equation (17) with initial condition (18). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
