-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2011; 1(2): 41-47
doi:10.5923/j.ajcam.20110102.08
Application of Multiple Exp-Function Method to Obtain Multi-Soliton Solutions of (2 + 1)- and (3 + 1)-Dimensional Breaking Soliton Equations
M. T. Darvishi1, Maliheh Najafi2, Mohammad Najafi2
1Department of Mathematics, Razi University, Kermanshah 67149, Iran
2Young Researchers Club, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran
Correspondence to: M. T. Darvishi, Department of Mathematics, Razi University, Kermanshah 67149, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The multiple exp-function method is a new approach to obtain multiple wave solutions of nonlinear partial differential equations (NLPDEs). By this method one can obtain multi-soliton solutions of NLPDEs. In this paper, using computer algebra systems, we apply the multiple exp-function method to construct the exact multiple wave solutions of the (2 + 1)- and the (3 + 1)-dimensional breaking soliton equations. By this application, we obtain one-wave, two-wave and three-wave solutions for these equations.
Keywords: Multiple Exp-Function Method, Breaking Soliton Equation, Exact Solution, Multi-Soliton Solution
Cite this paper: M. T. Darvishi, Maliheh Najafi, Mohammad Najafi, Application of Multiple Exp-Function Method to Obtain Multi-Soliton Solutions of (2 + 1)- and (3 + 1)-Dimensional Breaking Soliton Equations, American Journal of Computational and Applied Mathematics , Vol. 1 No. 2, 2011, pp. 41-47. doi: 10.5923/j.ajcam.20110102.08.
Article Outline
1. Introduction
- The study of exact solutions of nonlinear partial differential equations plays an important role in soliton theory and explicit formulas of nonlinear partial differential equations play an essential role in the nonlinear science. Also, the explicit formulas may provide physical information and help us to understand the mechanism of related physical models. Recently, many kinds of powerful methods have been proposed to find exact solutions of nonlinear partial differential equations, e.g., the tanh-method[1], the homogeneous balance method[2], homotopy analysis method[3-8], the
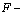 expansion method [9], three-wave method[10-13], extended homoclinic test approach[14-16], the
expansion method [9], three-wave method[10-13], extended homoclinic test approach[14-16], the 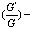 expansion method[17] and the exp-function method[18-23].By these analytic methods, one only can obtain traveling wave solutions for NLPDEs. However, it is known that there are multiple wave solutions to some NLPDEs, for example, multi-soliton solutions to KdV and Toda lattice equations[24] or multiple periodic wave solutions to the Hirota bilinear equations[25,26]. Recently, Ma and Fan[27] explored a key feature of the linear superposition principle that linear equations possess, for Hirota bilinear equations, while aiming to construct a specific sub-class of
expansion method[17] and the exp-function method[18-23].By these analytic methods, one only can obtain traveling wave solutions for NLPDEs. However, it is known that there are multiple wave solutions to some NLPDEs, for example, multi-soliton solutions to KdV and Toda lattice equations[24] or multiple periodic wave solutions to the Hirota bilinear equations[25,26]. Recently, Ma and Fan[27] explored a key feature of the linear superposition principle that linear equations possess, for Hirota bilinear equations, while aiming to construct a specific sub-class of 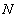 -soliton solutions formed by linear combinations of exponential traveling waves. They proved that, a linear superpositionprinciple can apply to exponential traveling waves of Hirota bilinear equations. Applications made to show that the presented linear superposition principle is helpful in generating
-soliton solutions formed by linear combinations of exponential traveling waves. They proved that, a linear superpositionprinciple can apply to exponential traveling waves of Hirota bilinear equations. Applications made to show that the presented linear superposition principle is helpful in generating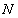 -wave solutions to soliton equations, particularly those in higher dimensions. Also, Ma et al.[28] constructed the multiple exp-function method to obtain multiple wave solutions, including one-soliton, two-soliton and three-soliton type solutions to (3+1)-dimensional YTSF equation. One may find another works to find exact solutions of soliton equations in[29-31].In this paper, we apply the multiple exp-function method to obtain some exact multiple wave solutions for the (2 + 1)- and (3 + 1)-dimensional breaking soliton equations.The (2+1)-dimensional breaking soliton equation is
-wave solutions to soliton equations, particularly those in higher dimensions. Also, Ma et al.[28] constructed the multiple exp-function method to obtain multiple wave solutions, including one-soliton, two-soliton and three-soliton type solutions to (3+1)-dimensional YTSF equation. One may find another works to find exact solutions of soliton equations in[29-31].In this paper, we apply the multiple exp-function method to obtain some exact multiple wave solutions for the (2 + 1)- and (3 + 1)-dimensional breaking soliton equations.The (2+1)-dimensional breaking soliton equation is 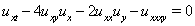 | (1) |
 -axis with a long wave propagated along the
-axis with a long wave propagated along the  -axis[32]. Wazwaz[33] introduced an extension to equation (1) by adding the last three terms with
-axis[32]. Wazwaz[33] introduced an extension to equation (1) by adding the last three terms with  replaced by
replaced by 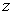 . His work, enables us to establish the following (3+1)-dimensional breaking soliton equation
. His work, enables us to establish the following (3+1)-dimensional breaking soliton equation 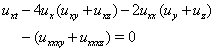 | (2) |
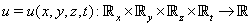 This paper is organized as follows: in the following section we have a brief review on multiple exp-function method. In Sections 3 and 4 we apply the exp-function method on the (2 + 1)-dimensional and the (3 + 1)-dimensional breaking soliton equations, respectively. In those sections we obtain one-wave, two-wave and three-wave solutions for our equations. The paper is concluded in Section 4.
This paper is organized as follows: in the following section we have a brief review on multiple exp-function method. In Sections 3 and 4 we apply the exp-function method on the (2 + 1)-dimensional and the (3 + 1)-dimensional breaking soliton equations, respectively. In those sections we obtain one-wave, two-wave and three-wave solutions for our equations. The paper is concluded in Section 4.2. Methodology
- Ma et al.[28] illustrated the multiple exp-function method in three steps. In summary, their steps are: Defining solvable differential equations, transforming nonlinear PDEs and solving algebraic systems. The key point of their approach is to seek rational solutions in a set of new variables defining individual waves. The application of multiple exp-function method yields specific one-wave, two-wave and three-wave solutions to NLPDEs. To explain these fundamental steps in multiple exp-function method, consider a PDE in (1 + 1) dimensions as
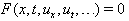 | (3) |
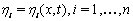 , by solvable partial differential equations, for example, the linear PDEs,
, by solvable partial differential equations, for example, the linear PDEs, 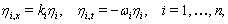 | (4) |
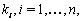 are the angular wave numbers and
are the angular wave numbers and 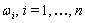 , are the wave frequencies. This step is a starting point to construct exact solutions of nonlinear equations. Solving these linear equations leads to the exponential function solutions,
, are the wave frequencies. This step is a starting point to construct exact solutions of nonlinear equations. Solving these linear equations leads to the exponential function solutions, 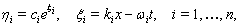 | (5) |
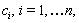 are arbitrary constants. Any function
are arbitrary constants. Any function 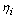 describing a single wave and a multiple wave solution will be a combination of all of those single waves. In the second step, we proceed by considering rational solutions in the new variables
describing a single wave and a multiple wave solution will be a combination of all of those single waves. In the second step, we proceed by considering rational solutions in the new variables 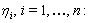
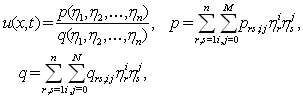 | (6) |
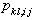 and
and 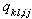 are constants to be determined from (3). Then we use the differential relations in (4) to express all partial derivatives of
are constants to be determined from (3). Then we use the differential relations in (4) to express all partial derivatives of 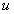 with
with 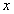 and
and 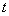 in terms of
in terms of 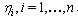 Substituting these obtained expressions for partial derivatives into the equation (3) generates a rational function equation in the new variables
Substituting these obtained expressions for partial derivatives into the equation (3) generates a rational function equation in the new variables 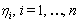 :
: 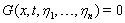 | (7) |
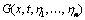 to zero. This yields a system of algebraic equations on all variables
to zero. This yields a system of algebraic equations on all variables 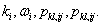 By solving this system, with the aid of a mathematical software such as Maple, we determine polynomials
By solving this system, with the aid of a mathematical software such as Maple, we determine polynomials 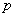 and
and 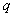 and the wave exponents
and the wave exponents 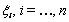 . After this, the multiple wave solution
. After this, the multiple wave solution 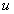 is computed and given by
is computed and given by 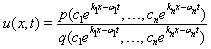 | (8) |
3. One-Wave, Two-Wave and Three- Wave Solutions to the (2 + 1) -Dimensional Breaking Soliton Equation
- In this part, we apply the multiple exp-function method to construct the exact multiple wave solutions of the (2 + 1) -dimensional breaking soliton equation
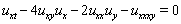 | (9) |
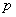 and
and 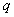 as follows:Case i: One-wave solutionsTo obtain one-wave solutions, we require the linear conditions
as follows:Case i: One-wave solutionsTo obtain one-wave solutions, we require the linear conditions 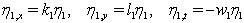 | (10) |
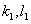 and
and 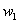 are constants which will be determined. Then we try a pair of polynomials of degree one,
are constants which will be determined. Then we try a pair of polynomials of degree one, 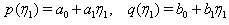 | (11) |
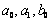 and
and 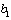 are constants to be determined. By the multiple exp-function method and using the differential relations in (10), we obtain the following solution to the resulting algebraic system with the aid of Maple,
are constants to be determined. By the multiple exp-function method and using the differential relations in (10), we obtain the following solution to the resulting algebraic system with the aid of Maple, 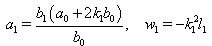 | (12) |
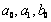 are arbitrary. Thus we can have an exponential function solution to (10),
are arbitrary. Thus we can have an exponential function solution to (10), 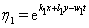 | (13) |
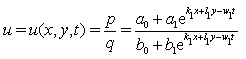 | (14) |
 and
and  are arbitrary constants. It must be noted that, if we set
are arbitrary constants. It must be noted that, if we set 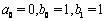 and
and 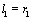 , the solution (19) of[33] will obtain.Case ii: Two-wave solutionsIn this case, we require the linear conditions,
, the solution (19) of[33] will obtain.Case ii: Two-wave solutionsIn this case, we require the linear conditions, 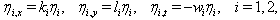 | (15) |
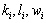 ,
, 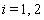 , are constants and thus the solutions
, are constants and thus the solutions 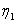 and
and 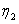 are defined by
are defined by 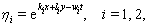 | (16) |
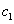 and
and 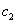 are arbitrary constants.We suppose that
are arbitrary constants.We suppose that 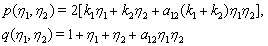 | (17) |
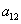 is a constant to be determined. By the multiple exp-function method and using the differential relations in (15), we obtain the following solution to the resulting algebraic system with the aid of Maple,
is a constant to be determined. By the multiple exp-function method and using the differential relations in (15), we obtain the following solution to the resulting algebraic system with the aid of Maple, 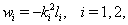 | (18) |
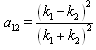 | (19) |
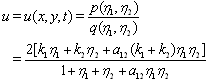 | (20) |
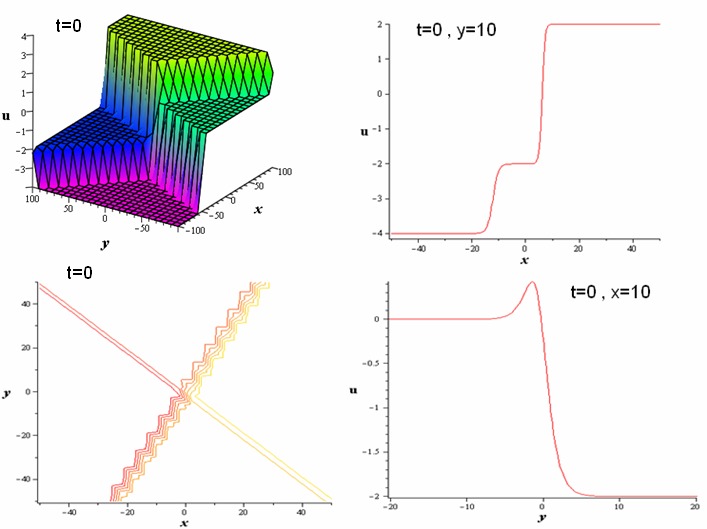 | Figure 1. The two-wave solution |
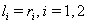 , solution (20) is as same as solution (24) of[33].We obtained a wide class of traveling wave solutions to Eq. (9) by setting special values to the arbitrary parameters, we can construct formal two-wave solutions. For instance, taking
, solution (20) is as same as solution (24) of[33].We obtained a wide class of traveling wave solutions to Eq. (9) by setting special values to the arbitrary parameters, we can construct formal two-wave solutions. For instance, taking 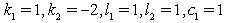 and
and 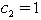 in (20) reveals solitary waves to Eq. (9). Figure 1 shows the plot of solution (20) for these special values of its parameters.Case iii: Three-wave solutions Similarly, to obtain the three-wave solutions for equation (9), we require the linear conditions,
in (20) reveals solitary waves to Eq. (9). Figure 1 shows the plot of solution (20) for these special values of its parameters.Case iii: Three-wave solutions Similarly, to obtain the three-wave solutions for equation (9), we require the linear conditions, 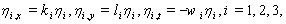 | (21) |
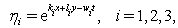 | (22) |
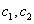 and
and 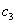 are arbitrary constants.We suppose that
are arbitrary constants.We suppose that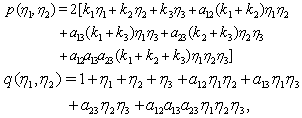 | (23) |
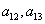 and
and 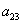 are constants to be determined. By the multiple exp-function method and using the differential relations in (21), we obtain the following solution to the resulting algebraic system with Maple,
are constants to be determined. By the multiple exp-function method and using the differential relations in (21), we obtain the following solution to the resulting algebraic system with Maple, 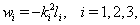 | (24) |
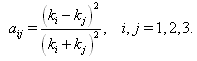 | (25) |
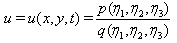 | (26) |
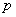 and
and 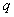 are defined by (23) and
are defined by (23) and 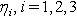 are defined by (22). For
are defined by (22). For 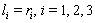 in (26), we meet solution (26) of [32]. Figure 2 shows the plot of solution (26) for some special values of its parameters.
in (26), we meet solution (26) of [32]. Figure 2 shows the plot of solution (26) for some special values of its parameters.4. One-Wave, Two-Wave and Three- Wave Solutions to the (3 + 1) -Dimensional Breaking Soliton Equation
- In this section, we will apply the multiple exp-function method to construct the exact multiple wave solutions for the (3 + 1)-dimensional breaking soliton equation
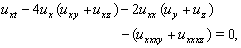 | (27) |
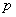 and
and 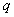 to generate one-wave, two-wave and three-wave solutions as follows:Case i: One-wave solutionsAgain, we require the linear conditions,
to generate one-wave, two-wave and three-wave solutions as follows:Case i: One-wave solutionsAgain, we require the linear conditions,  | (28) |
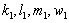 are constants. We then try a pair of polynomials of degree one,
are constants. We then try a pair of polynomials of degree one, 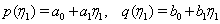 | (29) |
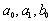 and
and 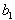 are constants to be determined. By the multiple exp-function method and using the differential relations in (28), we obtain the following solution to the resulting algebraic system with the help of Maple,
are constants to be determined. By the multiple exp-function method and using the differential relations in (28), we obtain the following solution to the resulting algebraic system with the help of Maple, 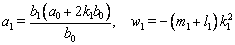 | (30) |
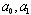 and
and  are arbitrary constants. Since we can have an exponential function solution to (28),
are arbitrary constants. Since we can have an exponential function solution to (28),  | (31) |
 | Figure 2. The three-wave solution. |
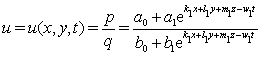 | (32) |
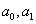 and
and 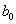 are arbitrary constants. For
are arbitrary constants. For 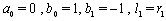 and
and 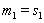 our solution (32) is the same solution (49) of [33].Case ii: Two-wave solutionsIn this case, we require the linear conditions,
our solution (32) is the same solution (49) of [33].Case ii: Two-wave solutionsIn this case, we require the linear conditions, 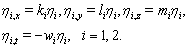 | (33) |
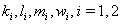 , are constants and thus the solutions
, are constants and thus the solutions 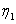 and
and 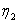 can be defined by
can be defined by 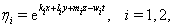 | (34) |
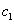 and
and 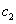 are arbitrary constants.We suppose that
are arbitrary constants.We suppose that 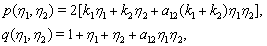 | (35) |
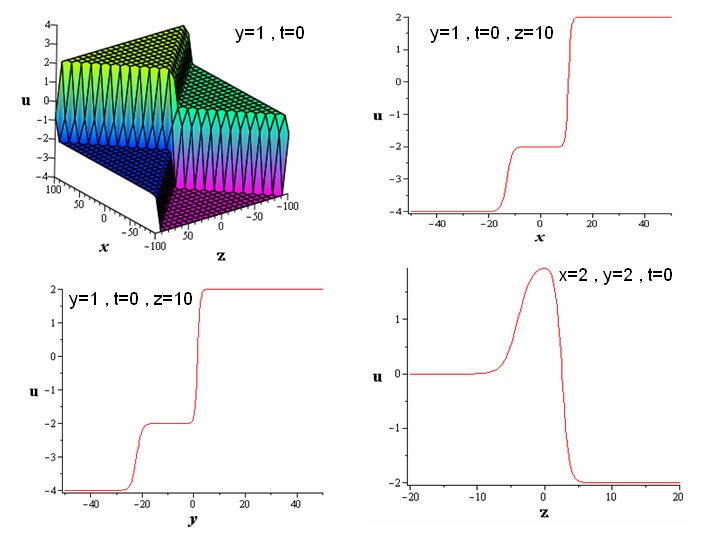 | Figure 3. The first two-wave solution. |
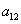 is a constant to be determined. By the multiple exp-function method and using the differential relations in (33), we obtain two solutions to the resulting algebraic system with Maple,
is a constant to be determined. By the multiple exp-function method and using the differential relations in (33), we obtain two solutions to the resulting algebraic system with Maple, 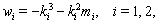 | (36) |
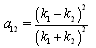 | (37) |
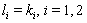 , and
, and 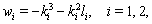 | (38) |
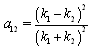 | (39) |
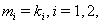 we obtain the following two-wave solutions
we obtain the following two-wave solutions 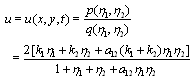 | (40) |
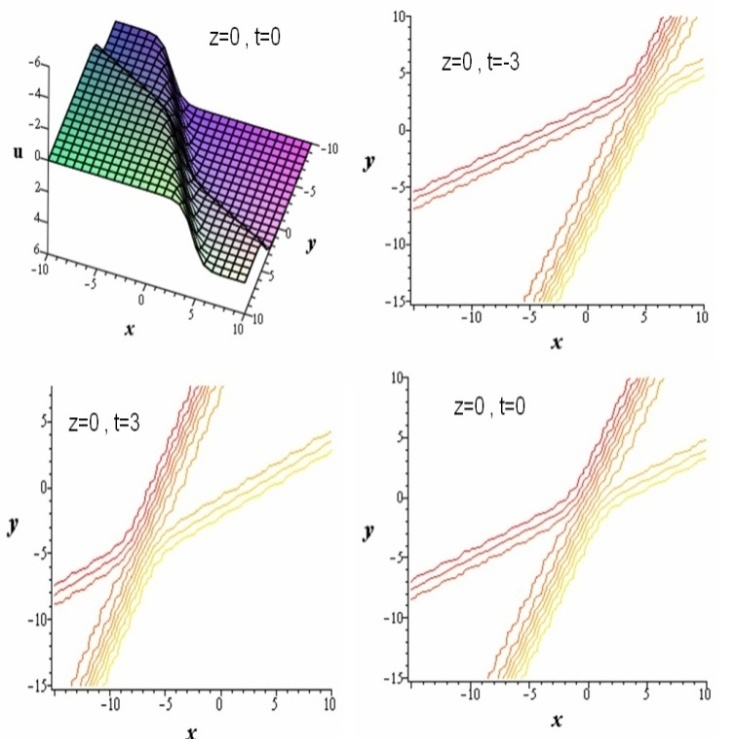 | Figure 4. The second two-wave solution. |
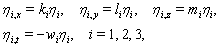 | (41) |
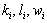 ,
, 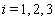 , are constants and thus the solutions
, are constants and thus the solutions 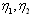 and
and 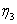 can be defined by
can be defined by 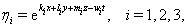 | (42) |
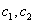 and
and 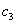 are arbitrary constants.We suppose that
are arbitrary constants.We suppose that 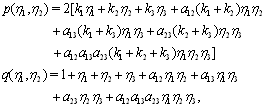 | (43) |
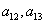 and
and 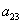 are constants to be determined. By the multiple exp-function method and using the differential relations in (41), we obtain the following solution to the resulting algebraic system with the help of Maple,
are constants to be determined. By the multiple exp-function method and using the differential relations in (41), we obtain the following solution to the resulting algebraic system with the help of Maple, 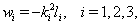 | (44) |
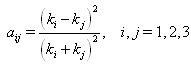 | (45) |
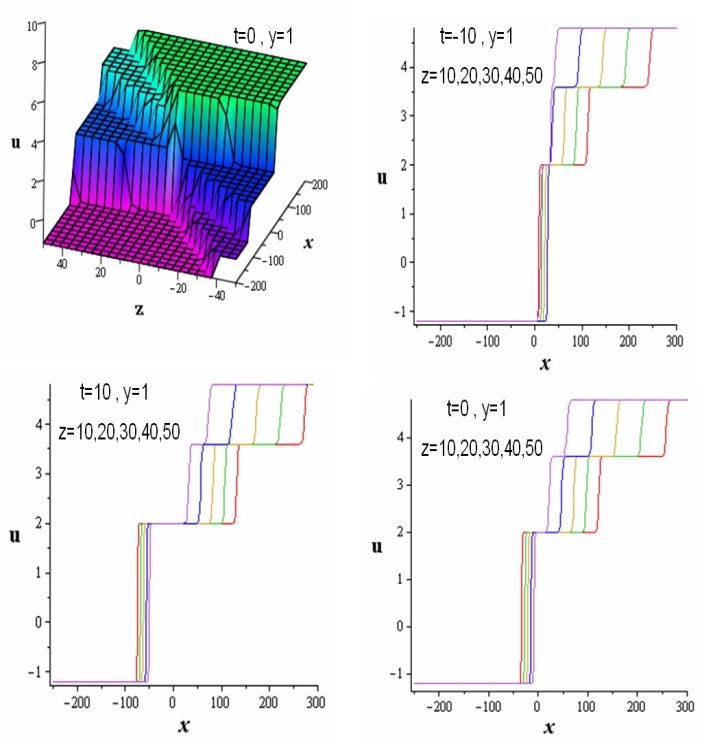 | Figure 5. The first three-wave solution. |
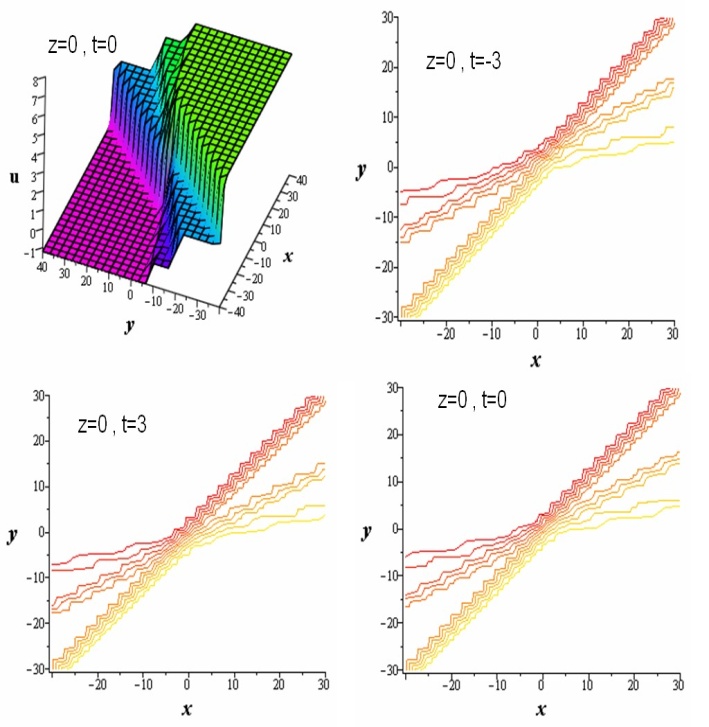 | Figure 6. The second three-wave. |
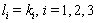 , and
, and 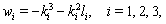 | (46) |
 | (47) |
 .Then, we obtain the following three-wave solutions for equation (27)
.Then, we obtain the following three-wave solutions for equation (27)  | (48) |
5. Conclusions
- In this paper, we have applied the multiple exp-function method to obtain one-wave, two-wave and three-wave solutions of the (2 + 1)- and the (3 + 1)-dimensional breaking soliton equations. These solutions are new solutions for these equations and for some special values of parameters in these new solutions we can obtain the solutions which have obtained by another methods. The multiple exp-function method is oriented towards the ease of use and capability of computer algebra systems and provides a straightforward and systematic solution procedure that generalizes Hirota's perturbation method. The method can be applied on other nonlinear partial differential equations which have multi-soliton solutions, because the multiple exp-function algorithm is powerful in generating exact solutions of nonlinear equations.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML