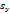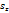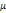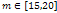-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2011; 1(1): 33-40
doi: 10.5923/j.ajcam.20110101.07
A Robust Method for Shape from Shading Using Genetic Algorithm Based on Matrix Code
R. F. Mansour
Department of Science and Mathematics, Faculty of Education, New Valley, Assiut University, EL kharaga, Egypt
Correspondence to: R. F. Mansour , Department of Science and Mathematics, Faculty of Education, New Valley, Assiut University, EL kharaga, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, a method for reconstructing a 3-D shape of an object from a 2-D shading image using a Genetic Algorithm (GA), which is an optimizing technique based on mechanisms of natural selection. The 3D-shape is recovered through the analysis of the gray levels in a single image of the scene. This problem is ill-posed except if some additional assumptions are made. In the proposed method, shape from shading is addressed as an energy minimization problem. The traditional deterministic approach provides efficient algorithms to solve this problem in terms of time but reaches its limits since the energy associated with shape from shading can contain multiple deep local minima. Genetic Algorithm is used as an alternative approach which is efficient at exploring the entire search space. The Algorithm is tested in both synthetic and real image and is found to perform accurate and efficient results.
Keywords: Genetic Algorithm; Shape for Shading; Fitness Function and Optimization
Cite this paper: R. F. Mansour , "A Robust Method for Shape from Shading Using Genetic Algorithm Based on Matrix Code", American Journal of Computational and Applied Mathematics , Vol. 1 No. 1, 2011, pp. 33-40. doi: 10.5923/j.ajcam.20110101.07.
Article Outline
1. Introduction
- SFS deals with the recovery of surface orientation and surface shape (highlight) from the gradual variation of shading in images. SFS is implemented by first modeling the image brightness as a function of surface geometry and then reconstructing a surface which, under the given imaging model, generates an image close to the input image. This field was formally introduced by Horn[1] and there have been many significant improvements in both theoretical and practical aspects of the problem. However, it has been shown that this is an ill-posed problem[2,3]. Surface shape recovery of observed objects is one of the main goals in the field of three-dimensional (3-D) computer vision. Marr identified shape-from shading (SFS) as providing one of the key routes to understanding 3D surface structure via the 2½D sketch[4]. The process has been an active area of research for over two decades. It is concerned with recovering 3D surface shape from shading patterns. The subject has been tackled in a variety of ways since the pioneering work of Horn[5]. They are classified into direct and indirect methods. Direct or active methods recover depth information directly using range finder and structure light. Indirect methods determine the relative depth by cues extracted from gray level images of observed object. This class contains shape from shading. Since the direct or active techniques usually involvemany complex external component setup, they may not be suitable for instance in object shape estimation. Hence many researchers have focused on the latter class of method. The shape from shading methods makes use of the change in image brightness of an object to determine the relative surface depth and can be effectively applied to smooth surface regions. Most of the shading techniques employ variation approaches which impose constraints such as smoothness, imaging equation and light conditions. As a result these techniques can only be applied to the object surface that satisfies the constraints. Also the computational complexity of the resulting algorithms is high and increases as the number of these constraints increases. Useful alternatives for variation shading are local shading and linear shading suggested by Pentland[6] this approach do not require prior information on the observed scene, imaging geometry and regularization. The assumption is that the surface shape is locally spherical, and the inclined light source is not allowed. Pentland[7] used the linear approximation of the reflectance function in terms of the surface gradient and applied a Fourier transform to the linear function to get a closed form solution for the depth at each point. Tsai and Shah[8] applied the discrete approximation of the gradient first, then employed the linear approximation of the reflectance function in terms of the depth directly. Their algorithm recovered the depth at each point using a Jacobi iterative scheme. As opposed to the previous methods on SFS, Samaras and Metaxas[9] presented a model-based approach, where shape from shading is incorporated as a nonlinear hard constraint within a deformable model framework. Recently, Zhao and Chellappa[10] provided a shape from shading approach for symmetric objects. A recent minimization based method proposed in[11] directly solves the shape by assuming the depth of the deepest surface point is known under constant albedo approximation. Alper and Mubarak[12] proposed a shape from shading (SFS) approach to recover both the shape and the reflectance properties of symmetric objects using a single image. The common constraint of constant or piece-wise constant albedo for Lambertian surfaces is relaxed to arbitrary albedo. The proposed method can be categorized as a linear shape from shading method, which linearizes the reflectance function for symmetric objects using the symmetry cues of the shape and the albedo, and iteratively computes the depth values. Estimated depth values are then used to recover pixel-wise surface albedo.In this study, the GA is applied to 3-D shape reconstruction of an object from a shading image of the object. In this method, arbitrary 3-D shapes are defined as individuals in a population according to the GA concept. The evaluation function of each individual is defined according to the correspondence between the 3-D shape represented by the individual and the measured 2-D shading image and other information about the object's 3-D shape, and then the optimized solution of the function is searched for using a GA. Accordingly, the 3-D shape represented by the individual having the highest value of the evaluation function is considered as the reconstructed 3-D shape of the object. The principle of the proposed method for reconstructing a 3-D shape from a 2-D shading image using a GA is described. For demonstration of the proposed method, 3-D shapes are reconstructed from shading images which are obtained by both computer simulation and experiment with a CCD camera. The reconstructed shapes are compared with shapes reconstructed by the conventional method of obtaining a shape from shading[13].
2. Related Works
- There are two ways to recover shape from a single image namely shape from shading and user interactive modeling [14]. The non-interactive methods compute depth based on the work proposed by Horn and Brook. This is done by minimizing the Eikonal equation and presenting the solution as computed depth. In the interactive method, the depth map obtained is interactively modified by the user in order to get more accurate results. Zhang et al.[15] classified shape from shading methods into four groups viz. minimization, propagation, local and linear methods. Zhang et al. implemented 6-well known algorithms and compared them objectively based on COP time and error. Although each algorithm works well with specific image, but produces poor results with others. In another work Durou et al.[16] classified shape from shading methods into three classes: minimization approaches, approximation approaches and partial differential equation based approaches. Patel and Smith[17] used a morphable model for shape from shading of non-Lambertian surfaces. Shlizerman and Basri[18] used the similarity between faces for 3D reconstruction. Common face features such as location of eyes, aspect ratio and the location of nose can vary between different races, gender or because of facial expressions. Using previously stored features their proposed algorithm guides the reconstruction of the face using information about the subject race, gender and facial expressions.
3. Problem Formulation
- We start by giving a brief outline of the SFS problem and introducing the basic assumptions. We attach to the camera a three-dimensional coordinate system (Oxyz), such that Oxy coincides with the image plane and Oz coincides with the optical axis. Under the assumption of orthographic projection, the visible part of the scene is, up to a scale factor, a graph z = u(x), where x = (x,y) is an image point. As is well known[19], the SFS problem can be modeled by the "image irradiance equation":
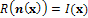 | (1) |
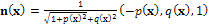 | (2) |
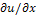 d and q =
d and q =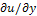 , so that
, so that 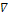 u(x) = (p(x), q(x)). Irradiance function I is the datum in the model since it is measured at each pixel of the image, for example in terms of a greylevel (from 0 to 255). To construct a continuous model, we will assume that I takes real values in the interval[0,1]. Height function u, which is the unknown of the problem, has to be reconstructed on a compact domain
u(x) = (p(x), q(x)). Irradiance function I is the datum in the model since it is measured at each pixel of the image, for example in terms of a greylevel (from 0 to 255). To construct a continuous model, we will assume that I takes real values in the interval[0,1]. Height function u, which is the unknown of the problem, has to be reconstructed on a compact domain 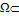 2, called the ‘‘reconstruction domain’’. Assume that there is a unique light source at infinity whose direction is indicated by the unit vector
2, called the ‘‘reconstruction domain’’. Assume that there is a unique light source at infinity whose direction is indicated by the unit vector 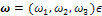 3. Also assume for simplicity that x is given (in some works, x as well is considered as unknown, see e.g.[20,21], even if this new problem is sometimes ill-posed[22]). Recalling that, for a Lambertian surface of uniform albedo equal to 1, R(n(x)) =
3. Also assume for simplicity that x is given (in some works, x as well is considered as unknown, see e.g.[20,21], even if this new problem is sometimes ill-posed[22]). Recalling that, for a Lambertian surface of uniform albedo equal to 1, R(n(x)) = 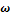 n(x), Eq.1 can be written, using Eq.2:
n(x), Eq.1 can be written, using Eq.2: 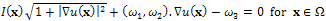 | (3) |
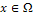 such that I(x) is maximal correspond to the particular situation where x and n(x) point in the same direction: these points are usually called ‘‘singular points’’. Let us mention that Eq. (3) is not the most general equation of SFS[23]: since real materials are not purely Lambertian, some publications are concerned with non-Lambertian SFS problems [24–26]; moreover, the situation is more complex in the presence of other lighting models[27,28] or when the interreflections are taken into account[29,30]. We will also consider the equation which appears in most of the papers and corresponds to frontal light source at infinity, i.e.
such that I(x) is maximal correspond to the particular situation where x and n(x) point in the same direction: these points are usually called ‘‘singular points’’. Let us mention that Eq. (3) is not the most general equation of SFS[23]: since real materials are not purely Lambertian, some publications are concerned with non-Lambertian SFS problems [24–26]; moreover, the situation is more complex in the presence of other lighting models[27,28] or when the interreflections are taken into account[29,30]. We will also consider the equation which appears in most of the papers and corresponds to frontal light source at infinity, i.e. 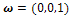 . Then Eq.3 becomes the "eikonal equation":
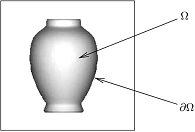
. Then Eq.3 becomes the "eikonal equation":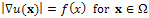 | (4) |
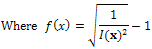 | (5) |
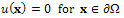 | (6) |
 | Figure 1. Object with occluding boundary, which might be used as boundary 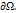 |
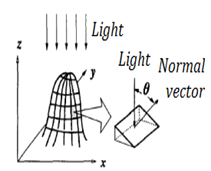 | Figure 2. The normal vector of the surface and the direction of the light source. |
4. Shape From Shading Using GA
4.1. Shading Images
- Gray levels in a shading image are determined by the orientation of the object surface. Assuming that the surface of the object is Lambertian, the gray levels of the shading image
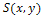 are expressed as the following Eq.7.
are expressed as the following Eq.7.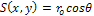 | (7) |
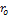 represents surface reflectance constant, and
represents surface reflectance constant, and 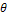 is the angle between the normal vector of the surface and the direction of the light source as shown in Figure. 2. In other words, a shading image of an 3-D object provides some information on the surface orientation of the object. However, the orientation cannot be uniquely determined. Therefore some constraint on the shape of the object is required for 3-D shape reconstruction from a shading image.
is the angle between the normal vector of the surface and the direction of the light source as shown in Figure. 2. In other words, a shading image of an 3-D object provides some information on the surface orientation of the object. However, the orientation cannot be uniquely determined. Therefore some constraint on the shape of the object is required for 3-D shape reconstruction from a shading image.4.2. Reconstruction Using GA
- In our proposed method, we assume that the constraints on the 3-D shape of an object are follows: (a) the boundary of the object in the shading image is specified, (b) the object does not have hollows and (c) the surface of the object is smooth.To apply a GA based matrix code , the candidates to be optimized must be coded as strings. In this method, a 3-D shape of the object is represented by a 2-D range image of L x L pixels with M levels, and then the range image is a coded string. Here, the pixels outside of the object boundary are set to zero according the condition (a). Figure. 3 shows the method for coding a 3-D shape. According to the coding method, the optimized 3-D shape is searched for using a GA as follows:
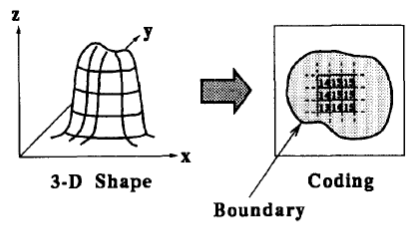 | Figure 3. The method for coding a 3-D shape. The string representing a 3-D shape is a range image of L x L pixels with M levels. |
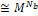 where
where 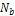 is the number of pixels inside the boundary of the object. accordingly, it becomes very difficult to find the optimal 3-D shape because the area to be searched is very wide. Hence, 3-D shapes represented by strings are restricted according to the condition (b), so that the total number of candidates of 3-D shapes can be reduced, and the efficiency of an optimal search can be improved. In making the initial population, strings are produced by matrix code. This method starts with an initial population P0 of size μ. This initial population is coded as a matrix of size μ× n called initial population matrix PM0. At every generation t, PMt is partitioned into v × η sub- matrices
is the number of pixels inside the boundary of the object. accordingly, it becomes very difficult to find the optimal 3-D shape because the area to be searched is very wide. Hence, 3-D shapes represented by strings are restricted according to the condition (b), so that the total number of candidates of 3-D shapes can be reduced, and the efficiency of an optimal search can be improved. In making the initial population, strings are produced by matrix code. This method starts with an initial population P0 of size μ. This initial population is coded as a matrix of size μ× n called initial population matrix PM0. At every generation t, PMt is partitioned into v × η sub- matrices 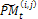 i = 1..., v, j = 1..., η, where v is the number of individuals on each partition and η is the number of genes on each partition. A crossover and mutation operators are applied on the partitioned sub-matrices and
i = 1..., v, j = 1..., η, where v is the number of individuals on each partition and η is the number of genes on each partition. A crossover and mutation operators are applied on the partitioned sub-matrices and 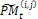 is updated. The range of each gene is divided into m sub-ranges in order to check the diversity of the gene values. The Gene Matrix GM is initialized to be the n × m zero matrix in which each entry of the i-th row refers to a sub-range of the i-th gene. While the search is processing, the entries of GM are updated if new values for a gene are generated within the corresponding sub-range. After having a GM full, i.e., with no zero entry, the search is learned that an advanced exploration process has been achieved. The Gene Matrix GM comes along with a certain number α predefined by the user. The zeros entries in GM are not immediately updated to be ones unless the number of individuals that have been generated inside a sub-range so far exceeds or equals αm. An example of GM with α = 0.2 in two dimensions is shown found in Figure. 4. In this figure the range of each gene is divided into ten sub-ranges. We can see that no individual has been generated inside the sub-ranges 1, 7 and 10 for the gene x1. However entry (1, 3) in GM0.2 is equal to 0 since there is only one individual lying inside the third sub-range and αm = 2. For the same reason, x2 has six zero-entries corresponding to six sub-ranges in which the number of generated individuals is less than αm. In a succeeding generation, if one or more individuals are generated inside the third sub-range for x1 for example, then entry (1, 3) will be set equal to one. In our experiments we used α as a function of log(n) and log(μ), where μ is the population size, in order to be suitable for all dimensions and for all population size. Moreover, the log function is used to estimate the value of α in order to reduce the complexity of increasing n or μ especially in high dimensional problems. Actually, the numerical experiments have showed that the best setting for number α is equal to 0.75 log2 n log μ. And then we calculate a fitness function for each string. Each string represents a 3-D shape that can determine a 2-D shading image. The fitness value of the string is defined according to the similarity the shading image determined by the string with the measured shading image. The fitness value
is updated. The range of each gene is divided into m sub-ranges in order to check the diversity of the gene values. The Gene Matrix GM is initialized to be the n × m zero matrix in which each entry of the i-th row refers to a sub-range of the i-th gene. While the search is processing, the entries of GM are updated if new values for a gene are generated within the corresponding sub-range. After having a GM full, i.e., with no zero entry, the search is learned that an advanced exploration process has been achieved. The Gene Matrix GM comes along with a certain number α predefined by the user. The zeros entries in GM are not immediately updated to be ones unless the number of individuals that have been generated inside a sub-range so far exceeds or equals αm. An example of GM with α = 0.2 in two dimensions is shown found in Figure. 4. In this figure the range of each gene is divided into ten sub-ranges. We can see that no individual has been generated inside the sub-ranges 1, 7 and 10 for the gene x1. However entry (1, 3) in GM0.2 is equal to 0 since there is only one individual lying inside the third sub-range and αm = 2. For the same reason, x2 has six zero-entries corresponding to six sub-ranges in which the number of generated individuals is less than αm. In a succeeding generation, if one or more individuals are generated inside the third sub-range for x1 for example, then entry (1, 3) will be set equal to one. In our experiments we used α as a function of log(n) and log(μ), where μ is the population size, in order to be suitable for all dimensions and for all population size. Moreover, the log function is used to estimate the value of α in order to reduce the complexity of increasing n or μ especially in high dimensional problems. Actually, the numerical experiments have showed that the best setting for number α is equal to 0.75 log2 n log μ. And then we calculate a fitness function for each string. Each string represents a 3-D shape that can determine a 2-D shading image. The fitness value of the string is defined according to the similarity the shading image determined by the string with the measured shading image. The fitness value 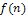 is expressed as the following Eq.8:
is expressed as the following Eq.8: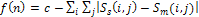 | (8) |
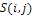 = a shading image determined by a string which is a candidate of the object shape,
= a shading image determined by a string which is a candidate of the object shape,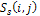 = smoothing image of S ( i , j ) ,
= smoothing image of S ( i , j ) ,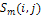 = the measured shading image,A smoothing image of
= the measured shading image,A smoothing image of 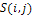 is expressed as
is expressed as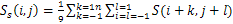 | (9) |
 is calculated according to equation (9). In the definition of the string fitness, a smoothing image of it shading image determined by a string is compared with the measured shading image. We consider this to mean that condition (c) is true.Secondary, arithmetical crossover and mutation operations are used in the proposed algorithm to crossover operation between individuals from the current population into next generation. We can defined in the following procedure.
is calculated according to equation (9). In the definition of the string fitness, a smoothing image of it shading image determined by a string is compared with the measured shading image. We consider this to mean that condition (c) is true.Secondary, arithmetical crossover and mutation operations are used in the proposed algorithm to crossover operation between individuals from the current population into next generation. We can defined in the following procedure. | Figure 4. An Example of the Gene Matrix in  . . |
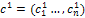 and
and 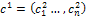 are generated from parents
are generated from parents 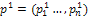 and
and 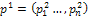 where
where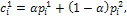
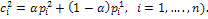 1- Return.The proposed method uses mutation operator by generating a new random value for the selected gene within its domain. Mutagenesis. In order to accelerate the search process, a special type of a directed mutation is applied. Actually, our method employs the mutagenesis operator [31]. Mutagenesis is used to alter some individuals selected for the next generation. The formal procedure for mutagenesis is given as follows.Procedure 2. Mutation(x,GM)1. If GM is full, then return; otherwise, go to Step 2.2. Choose a zero-position (i, j) in GM randomly.3. Update x by setting
1- Return.The proposed method uses mutation operator by generating a new random value for the selected gene within its domain. Mutagenesis. In order to accelerate the search process, a special type of a directed mutation is applied. Actually, our method employs the mutagenesis operator [31]. Mutagenesis is used to alter some individuals selected for the next generation. The formal procedure for mutagenesis is given as follows.Procedure 2. Mutation(x,GM)1. If GM is full, then return; otherwise, go to Step 2.2. Choose a zero-position (i, j) in GM randomly.3. Update x by setting 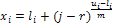 , where r is a random number from (0, 1) and li, ui are the lower and upper bounds of the variable
, where r is a random number from (0, 1) and li, ui are the lower and upper bounds of the variable 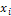 , respectively.4. Update GM and return.The algorithm described as follows. Initialization Set values of m, μ, v and η . Set the crossover and mutation probabilities pc
, respectively.4. Update GM and return.The algorithm described as follows. Initialization Set values of m, μ, v and η . Set the crossover and mutation probabilities pc 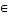 (0,1) and pm
(0,1) and pm 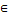 (0,1), respectively. Set the generation counter t := 0. Initialize GM as n × m zero matrix, and generate an initial population P0 of size μ and code it to a matrix
(0,1), respectively. Set the generation counter t := 0. Initialize GM as n × m zero matrix, and generate an initial population P0 of size μ and code it to a matrix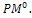 Parent selection. Evaluate the fitness function of all individuals coded in
Parent selection. Evaluate the fitness function of all individuals coded in 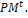 Select an intermediate population
Select an intermediate population 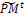 from the current one
from the current one 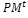 . 3- Partitioning and genetic operations. Partition
. 3- Partitioning and genetic operations. Partition 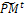 into v × η sub-matrices. Apply the following for all sub-matrices
into v × η sub-matrices. Apply the following for all sub-matrices 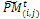 , i = 1..., η, j = 1..., v.3.1. Crossover. Associate a random number from (0, 1) with each row in
, i = 1..., η, j = 1..., v.3.1. Crossover. Associate a random number from (0, 1) with each row in 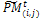 and add this individual to the parent pool if the associated number is less than pc. Apply Procedure crossover to all selected pairs of parents and update
and add this individual to the parent pool if the associated number is less than pc. Apply Procedure crossover to all selected pairs of parents and update 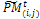 3.2. Mutation. Associate a random number from (0, 1) with each gene in each gene i
3.2. Mutation. Associate a random number from (0, 1) with each gene in each gene i 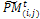 . Mutate the gene which their associated number less than pm by generating a new random value for the selected gene within its domain.4- Stopping condition. If GM is full, then go to Step 7. Otherwise, go to Step 5.5-Survivor selection. Evaluate the fitness function of all corresponding children in
. Mutate the gene which their associated number less than pm by generating a new random value for the selected gene within its domain.4- Stopping condition. If GM is full, then go to Step 7. Otherwise, go to Step 5.5-Survivor selection. Evaluate the fitness function of all corresponding children in 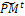 , and choose the μ best individuals from the parent and children populations to form the next generation
, and choose the μ best individuals from the parent and children populations to form the next generation 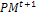 .6- Mutagenesis. Apply procedure 2 to alter the worst individuals in
.6- Mutagenesis. Apply procedure 2 to alter the worst individuals in 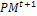 , set t:=t+1 and go to Step 2.7-Intensification. Apply a local search method starting from each solution from the Nelite elite ones obtained in the previous search stage.
, set t:=t+1 and go to Step 2.7-Intensification. Apply a local search method starting from each solution from the Nelite elite ones obtained in the previous search stage.5. Experimental
- It is very difficult to choose good test images for SFS algorithms. A good test image must match the assumptions of the algorithms, e.g. Lambertian reflectance model, constant albedo value, and infinite point source illumination. It is not difficult to satisfy these assumptions for synthetic images, but no real scene perfectly satisfies these conditions. In real images there will be errors to the extent that these assumptions are not matched. In this section, we describe the images chosen to test the SFS algorithms.
 | Figure 5. Synthetic images generated using two different light sources: (a) Synthetic Vase (0, 0, 1), (b) Mozart (0, 0, 1), (c) Synthetic Vase (1, 0, 1) and (d) Mozart (1, 0, 1). |
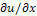 and q =
and q = 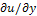 using the forward discrete approximation of the depth, u and generated shaded images using the Lambertian reflectance model. There are at least two advantages of using synthetic images. First, we can generate shaded images with different light source directions for the same surface. Second, with the true depth information, we can compute the error and compare the performance. However, the disadvantage of using synthetic images is that performance on synthetic images cannot be used reliably to predict performance on real images. In our study we used two synthetic surfaces (Synthetic Vase and, Mozart), with two different light sources ((0, 0, 1) and (1, 0, 1)). Also in our study we used three real images (Lenna, Pepper and Vase), shown in Figures. 5 and 6. The light source directions for these images are the following: for the Lenna image light source direction is (1.5, 0.866, 1). And Pepper image light source direction is (0.766, 0.642, 1), finally Vase image is (-0.939, 1.867, 1.0).
using the forward discrete approximation of the depth, u and generated shaded images using the Lambertian reflectance model. There are at least two advantages of using synthetic images. First, we can generate shaded images with different light source directions for the same surface. Second, with the true depth information, we can compute the error and compare the performance. However, the disadvantage of using synthetic images is that performance on synthetic images cannot be used reliably to predict performance on real images. In our study we used two synthetic surfaces (Synthetic Vase and, Mozart), with two different light sources ((0, 0, 1) and (1, 0, 1)). Also in our study we used three real images (Lenna, Pepper and Vase), shown in Figures. 5 and 6. The light source directions for these images are the following: for the Lenna image light source direction is (1.5, 0.866, 1). And Pepper image light source direction is (0.766, 0.642, 1), finally Vase image is (-0.939, 1.867, 1.0). | Figure 6. Real images: (a) Lenna. (b) Pepper. (c) Vase |
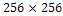 . Table 1 summarizes the parameters of each image
. Table 1 summarizes the parameters of each image
|
 | Figure 9. Results for Zheng and Chellappa's method on real images: (a) Lenna. (b) Pepper. (c) Vase |
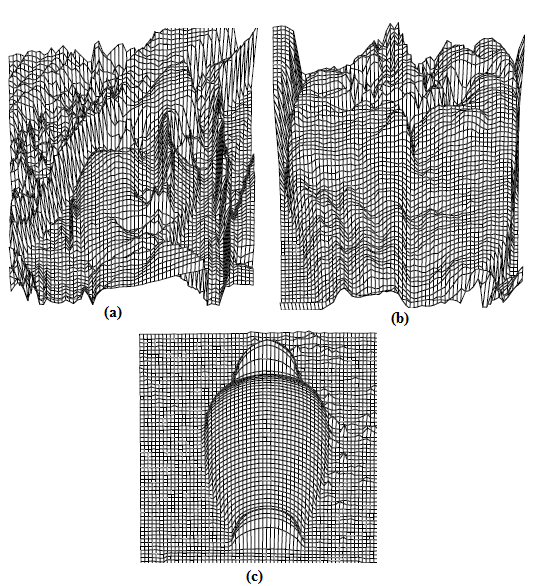 | Figure 10. Results for Tsai and Shah's method on real images: (a) Lenna. (b) Pepper. (c) Vase. |
 ,
,  ,
, 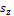 and
and 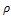 were estimated by Zheng and Chellappa method. The parameter
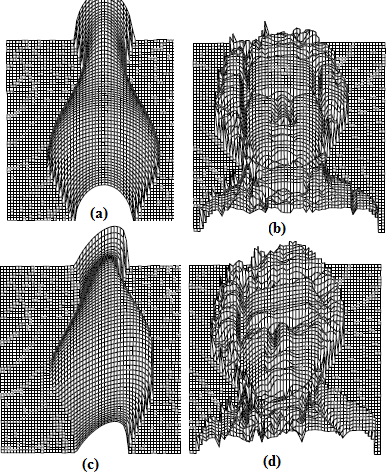
were estimated by Zheng and Chellappa method. The parameter 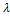 is always positive, and was determined experimentally. Figure. (11) shows the experimental results of a synthetic Mozart image. Figure (11.a) shows the original image. The surface recovered by our approach is shown in Figure (11.b). In order to verify the accuracy of the proposed approach, it was necessary to apply our algorithm on natural images. The next examples show the results obtained by applying our approach to the Pepper ,Vase, and Lenna. The recovered surface is shown in Figures (12, 13 and 14). For the reconstructed pepper image in Figure (13), there is some errors due to albedo discontinuities and self-occlusions, which violate the assumptions of the algorithm[32]. The effect of different GA parameters on the reconstruction accuracy is investigated. The GA parameters used in the algorithm are summarized in Table 2.
is always positive, and was determined experimentally. Figure. (11) shows the experimental results of a synthetic Mozart image. Figure (11.a) shows the original image. The surface recovered by our approach is shown in Figure (11.b). In order to verify the accuracy of the proposed approach, it was necessary to apply our algorithm on natural images. The next examples show the results obtained by applying our approach to the Pepper ,Vase, and Lenna. The recovered surface is shown in Figures (12, 13 and 14). For the reconstructed pepper image in Figure (13), there is some errors due to albedo discontinuities and self-occlusions, which violate the assumptions of the algorithm[32]. The effect of different GA parameters on the reconstruction accuracy is investigated. The GA parameters used in the algorithm are summarized in Table 2. | Figure 11. Results for our method on synthetic image “Mozart”. |
 | Figure 12. Results for our method on real image “Pepper”. |
| |||||||||||||||||||||||||||||||
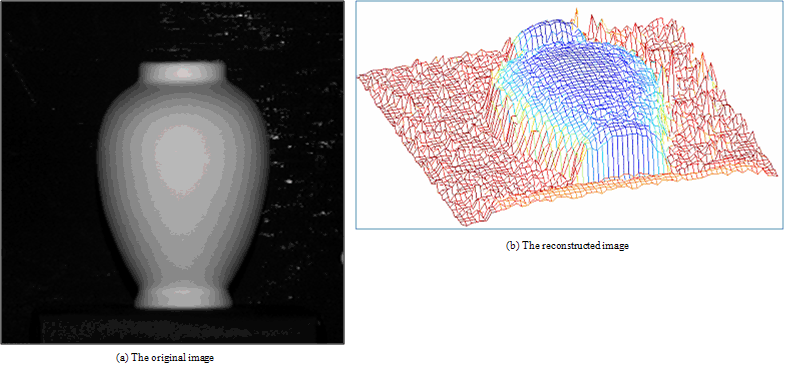 | Figure 13. Results for our method on real image “Vase” |
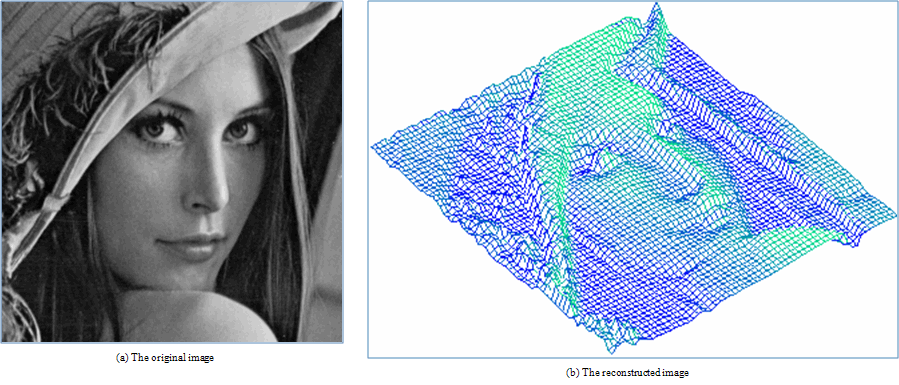 | Figure 14. Results for our method on real image “Lenna” |
6. Conclusions
- In this paper, a new method for solving the Shape from Shading problem using GA based on matrix code has been developed. The novelty of the proposed technique comes from the GA itself. This has been achieved by applying an efficient multi objective function with the brightness and smoothness constrains. Several GA design parameters have been studied to illustrate their effects on the algorithm convergence. The proposed method is tested in both synthetic and real image and is found to perform accurate and efficient results as shown in Table 3.
References
| [1] | A. Meyer, H. M. Briceno, and S. Bouakaz, User-guided Shape from Shading to Reconstruct Fine Details from a Single Photograph. 8th Asian Conference on Computer Vision, Tokyo, Japan. Identifying LIRIS, 2007 |
| [2] | J. D Durou, L. Mascarilla, and D. Piau, Non-Visible Deformations. In: 9th International Conference on Image Analysis and Processing - ICIAP’97, Florence, Italie, 1997 |
| [3] | E. Prados, and O. Faugeras, Shape from shading: a wellposed problem ? In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, California, vol. 2, IEEE, pp. 870–877, 2005 |
| [4] | D. C. Marr, Colour indexing, Int. J. Computer. Vision, vol. 7, pp.11-32, 1982 |
| [5] | K. Ikeuchi, B. K. P. Horn, Numerical shape from shading and occluding boundaries, Artif. Intell. vol. 17, no.3, pp.141-184, 1981 |
| [6] | A. Pentland, Local shading analysis, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 6, No.2, pp.170-187, 1984 |
| [7] | P. S. Tsai, and M. Shah, Shape from shading using linear approximation, Image and Vision Computing Journal, vol.12(8) pp.487-498, 1994 |
| [8] | P. S. Tsai, and M. Shah, A Fast Linear Shape from Shading, IEEE Computer Vision and Pattern Recognition, pp. 734-736, 1992 |
| [9] | D. Samaras, and D. Metaxas, Incorporating Illumination Constraints in Deformable Models for Shape from Shading and Light Direction Estimation, IEEE transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 2 pp. 247-264, 2003 |
| [10] | W. Zhao, and R. Chellappa, Illumination insensitive face recognition using symmetric shape from shading, In IEEE Conference on Computer Vision and Pattern Recognition, pp. 286-293, 2000 |
| [11] | R. Kimmel, and J. A. Sethian, Optimal algorithm for shape from shading and path planning, JMIV Journal, vol. 14, no.3, pp. 237-244, 2001 |
| [12] | Y. Alper, and S. Mubarak, Estimation of Arbitrary Albedo and Shape from Shading for Symmetric Objects, Proceedings of British Machine Vision Conference, Cardiff, England, pp. 728-736, 2002 |
| [13] | S. Yin, Y. Tsui and C. Chow, "A fast marching formulation of perspective shape from shading under frontal illumination" ,Pattern Recognition Letters vol. 28, pp.806–824, 2007 |
| [14] | G. Zeng, Y. Matsushita, L. Quan, and H. Y. Shum, Interactive Shape from Shading. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, vol. I, San Diego, California, USA, pp.343–350, 2005 |
| [15] | R. Zhang, P. S. Tsai, J. E. Cryer, and M. Shah, Shape from Shading: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, no. 21, vol. 8, pp. 690–706, 1999 |
| [16] | J. D. Durou, M. Falcone, and M. Sagona, A Survey of Numerical Methods for Shape from Shading. Rapport de Recherche 2004-2-R, Institut de Recherche en Informatique de Toulouse, Toulouse, France, 2004 |
| [17] | A. Patel and W. A. P. Smith, Shape-from-shading driven 3D Morphable Models for Illumination Insensitive Face Recognition. In Proc. BMVC, 2009 |
| [18] | I. K. Shlizerman, R. Basri, 3D Face Reconstruction from a Single Image Using a Single Reference Face Shape. In: Proceedings of IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, 2011 |
| [19] | B. K. P. Horn, M. J. Brooks (Eds.), Shape from Shading, MIT Press, 1989 |
| [20] | W. Chojnacki, M. J. Brooks, D. Gibbins, Revisiting Pentland’s estimator of light source direction, Journal of the Optical Society of America Part A: Optics, Image Science, and Vision, vol. 11, no. 1, pp. 118–124, 1994 |
| [21] | M. S. Drew, Direct solution of orientation-from-color problem using a modification of Pentland’s light source direction estimator, Computer Vision and Image Understanding vol. 64, no. 2, pp. 286–299, 1996 |
| [22] | P. N. Belhumeur, D. J. Kriegman, A. L. Yuille, The bas-relief ambiguity, International Journal of Computer Vision, vol. 35, no.1, pp. 33–44, 1999 |
| [23] | M. Oren, S. K. Nayar, Generalization of the Lambertian model and implications for machine vision, International Journal of Computer Vision 14 vol. 3, pp. 227–251, 1995 |
| [24] | S. M. Bakshi, Y. -H. Yang, Shape from shading for non-Lambertian surfaces, in: Proceedings of the IEEE International Conference on Image Processing (vol. II), Austin, TX, USA, pp. 130–134, 1994 |
| [25] | K. M. Lee, C. -C. J. Kuo, Shape from shading with a generalized reflectance map model, Computer Vision and Image Understanding 67 vol. 2, pp. 143–160, 1997 |
| [26] | H. Ragheb, E. R. Hancock, A probabilistic framework for specular shape-from-shading, Pattern Recognition, vol.36 No 2, pp. 407–427, 2003 |
| [27] | A. J. Stewart, M.S. Langer, Toward accurate recovery of shape from shading under diffuse lighting, IEEE Transactions on Pattern Analysis and Machine Intelligence vol. 19, no. 9, pp. 1020–1025. 1997 |
| [28] | Y. Wang, D. Samaras, Estimation of multiple illuminants from a single image of arbitrary known geometry, in: Proceedings of the Seventh European Conference on Computer Vision vol. 3, vol. 2352 of Lecture Notes in Computer Science, Copenhagen, Denmark, pp. 272–288, 2002 |
| [29] | S. K. Nayar, K. Ikeuchi, T. Kanade, Shape from interreflections, International Journal of Computer Vision , vol. 6, no. 3,pp.173–195, 1991 |
| [30] | D. A. Forsyth, A. Zisserman, Reflections on shading, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 13, no. 7, pp. 671–679, 1991 |
| [31] | A. Hedar, B. T. Ong and M. Fukushima, “Genetic algorithms with automatic accelerated termination,” Technical Report 2007-002, Department of Applied Mathematics and Physics, Kyoto University, (January 2007) |
| [32] | D. Samaras, and D. Metaxas, "Incorporating Illumination Constraints in Deformable Models for Shape from Shading and Light Direction Estimation", IEEE transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 2, 2003 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML