-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2011; 1(1): 27-32
doi: 10.5923/j.ajcam.20110101.06
Three-Dimensional Mixed Convection Flow past an Infinite Vertical Plate with Constant Surface Heat Flux
Bhupendra Kumar Sharma 1, Tara Chand 2, R. C. Chaudhary 2
1Department of Mathematics, Birla Institute of Technology & Science, Pilani, 333031, India
2Department of Mathematics, University of Rajasthan, Jaipur, 302004, India
Correspondence to: Bhupendra Kumar Sharma , Department of Mathematics, Birla Institute of Technology & Science, Pilani, 333031, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The present paper contains a mathematical analysis of the mixed convection three dimensional steady laminar flow of a viscous incompressible fluid past an infinite vertical porous plate. The three-dimensional flow is caused by the transverse sinusoidal suction at the plate. A constant heat flux is prescribed at the plate. Assuming the plate velocity to be uniform, analytical solutions are obtained for the flow field, the temperature field and the skin-friction. Effects of Prandtl number and Grashof number on the flow characteristics are explored and illustrated graphically.
Keywords: Three Dimensional, Mixed Convection, Heat Flux
Cite this paper: Bhupendra Kumar Sharma , Tara Chand , R. C. Chaudhary , "Three-Dimensional Mixed Convection Flow past an Infinite Vertical Plate with Constant Surface Heat Flux", American Journal of Computational and Applied Mathematics , Vol. 1 No. 1, 2011, pp. 27-32. doi: 10.5923/j.ajcam.20110101.06.
1. Introduction
- In view of the importance of the problems of laminar flow control (LFC), especially in the field of aeronautical engineering, various theoretical and experimental studies of different arrangements and configurations of suction holes and slits have been compiled by Lachmann[1]. The suction of the fluid is also an acknowledged technique for controlling the undesirable features in the boundary layer theory. Further, from the technological point of view, free convection flow and heat transfer problems are always important, for they have many practical applications. The phenomenon of free-convection arises when the difference between the plate temperature and the free stream temperature appreciably large which causes density variations leading to buoyancy forces acting on the fluid elements. This process of heat transfer is encountered in cooling of nuclear reactors, providing heat sinks in turbine blades and aeronautics. Free convection flow past vertical plate has been studied extensively by many researchers and some of them are Ostrach[2-3], Stewartson et. al.[4], Sparrow et. al.[5-6], Mabuchi[7], Riley et. al.[8], Berezovsky et.al.[9], Na[10], Dey et al [11], Kawase et al[12], Martynenko et.al.[13], Weiss et.al.[14] and Pantokratoras[15-16] in numerous ways to include various physical effects. In their work they have restricted themselves to two-dimensional flow only. There may arise situations where the flow fields may be essentially three-dimensional, for example when variations in the suction velocity distribution is transverse to the flow direc- tion. Gersten and Gross[17] have studied the effect of such a transverse sinusoidal suction velocity distribution on flow and heat transfer over a plane wall. Singh et.al[18] extended the idea of transverse suction velocity further to vertical porous plate. In references[17-18] the temperature of the plate was kept constant. In many problems, particularly those involving the cooling of electrical and nuclear components, the wall heat flux is specified. In such problems, over heating burnout and meltdown are very important issues. From practical stand point, an important wall model is considered with constant heat flux. In many applications, the wall heating effect is the result of radiation heating (the constant heat flux condition applies to nuclear radiation heating) from the other side or, as in the case of electronic components, the result of resistive heating (Bejan[19] ). The problems with prescribed heat flux are special cases of the vast analytically accessible class of problems. Sparrow et al[6], Merkin et al[20], Lee.et al.[21], Malarvizhi et.al.[22], Burak et. al.[23] and Pantokratoras[24] are some of the researchers who have investigated the convection flow with prescribed heat flux conditions. Injection and suction effects on three dimensional unsteady flow and heat transfer between two parallel porous plates have been studied by Chaudhary and Sharma[25]. Sharma et. al.[26] have studied the radiation effect on temperature distribution in three-dimensional Couette flow with injection or suction. Recently, three-dimensional unsteady mixed convection flow with periodic temperature studied by Sharma et. al.[27-29]. Approximate solutions of physical problems are handy tools in the hands of a scientist and an engineer. Though the advent of computers has opened new vistas for obtaining accurate numerical solutions of the problems of ever-increasing complexity, it has in no way diminished the utility of a judiciously produced approximate analytical solutions which are also fairly accurate. In the present paper, we present an approximate analytical solution to the problem of the laminar three-dimensional (caused by sinusoidally varying suction) steady mixed convection flow past an infinite vertical porous plate with constant heat flux, (CHF), from which the fluid is extracted at a uniform rate.
2. Mathematical Analysis
- We choose a coordinate system with plate lying vertically on x*-z* plane such that x*-axis is oriented in direction of the buoyancy force and y*-axis is perpendicular to the plane of the wall and directed into the fluid. The wall is moving with constant velocity U0. A constant suction velocity at the plane then leads to the two-dimensional asymptotic suction solution and the suction velocity transverse to the flow directions leads to cross-flow and hence the flow will be three-dimensional over the entire plane. We consider the sinusoidal suction velocity distribution of the form
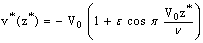 | (1) |
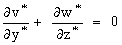 | (2) |
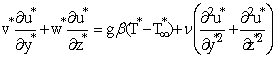 | (3) |
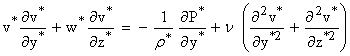 | (4) |
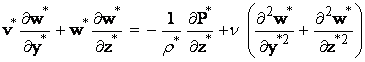 | (5) |
 | (6) |
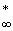 is the temperature in the free stream and κ is the thermal conductivity. For β ∇ T < < 1. We can express
is the temperature in the free stream and κ is the thermal conductivity. For β ∇ T < < 1. We can express 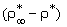 in terms of
in terms of 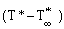 as
as 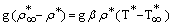 .The boundary conditions are:
.The boundary conditions are: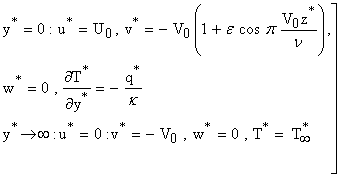 | (7) |

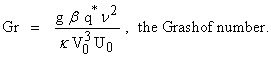 The equations (2) to (7) become
The equations (2) to (7) become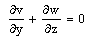 | (8) |
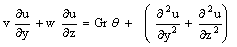 | (9) |
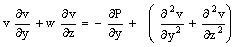 | (10) |
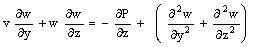 | (11) |
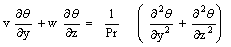 | (12) |
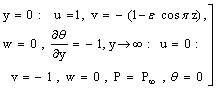 | (13) |
3. Solution
- When the amplitude ε < < 1, we assume the solution in the neighbourhood of the plate of the form
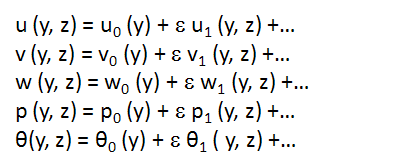 | (14) |
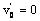 | (15) |
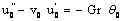 | (16) |
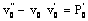 | (17) |
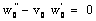 | (18) |
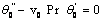 | (19) |
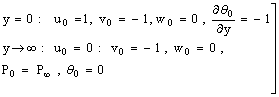 | (20) |
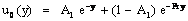 | (21) |
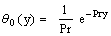 | (22) |
 and Pr ≠ 1This is the solution of a steady two-dimensional problem with constant suction and heat flux at the vertical plate. Taking into account the solutions of the transverse velocity components v0 and w0, when ε ≠ 0, substituting equation (14) in equations (8) to (12) and comparing the coefficients of like powers of ε , neglecting those of ε2 , we get the terms as the coefficient of ε give the following equations:
and Pr ≠ 1This is the solution of a steady two-dimensional problem with constant suction and heat flux at the vertical plate. Taking into account the solutions of the transverse velocity components v0 and w0, when ε ≠ 0, substituting equation (14) in equations (8) to (12) and comparing the coefficients of like powers of ε , neglecting those of ε2 , we get the terms as the coefficient of ε give the following equations: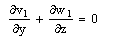 | (23) |
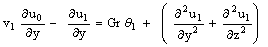 | (24) |
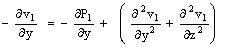 | (25) |
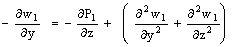 | (26) |
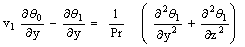 | (27) |
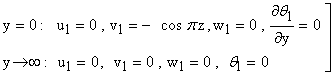 | (28) |
 | (29) |
 | (30) |
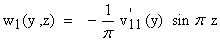 | (31) |
 | (32) |
 | (33) |
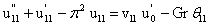 | (34) |
 | (35) |
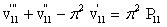 | (36) |
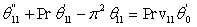 | (37) |
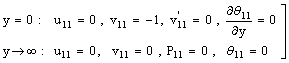 | (38) |
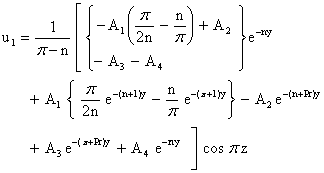 | (39) |
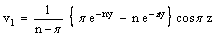 | (40) |
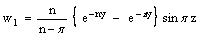 | (41) |
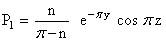 | (42) |
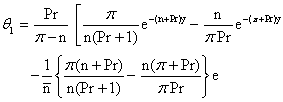 | (43) |
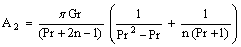 ,
,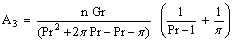 ,
,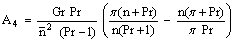 ,
,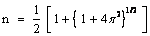 ,
,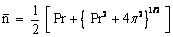 .Substituting equations (21), (39) and (22), (43) in equation (14) for u and θ, we get the expressions for the main flow velocity and the temperature profiles. The main flow velocity and the temperature can now be expressed in terms of fluctuating part as:
.Substituting equations (21), (39) and (22), (43) in equation (14) for u and θ, we get the expressions for the main flow velocity and the temperature profiles. The main flow velocity and the temperature can now be expressed in terms of fluctuating part as: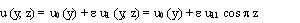 | (44) |
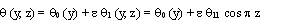 | (45) |
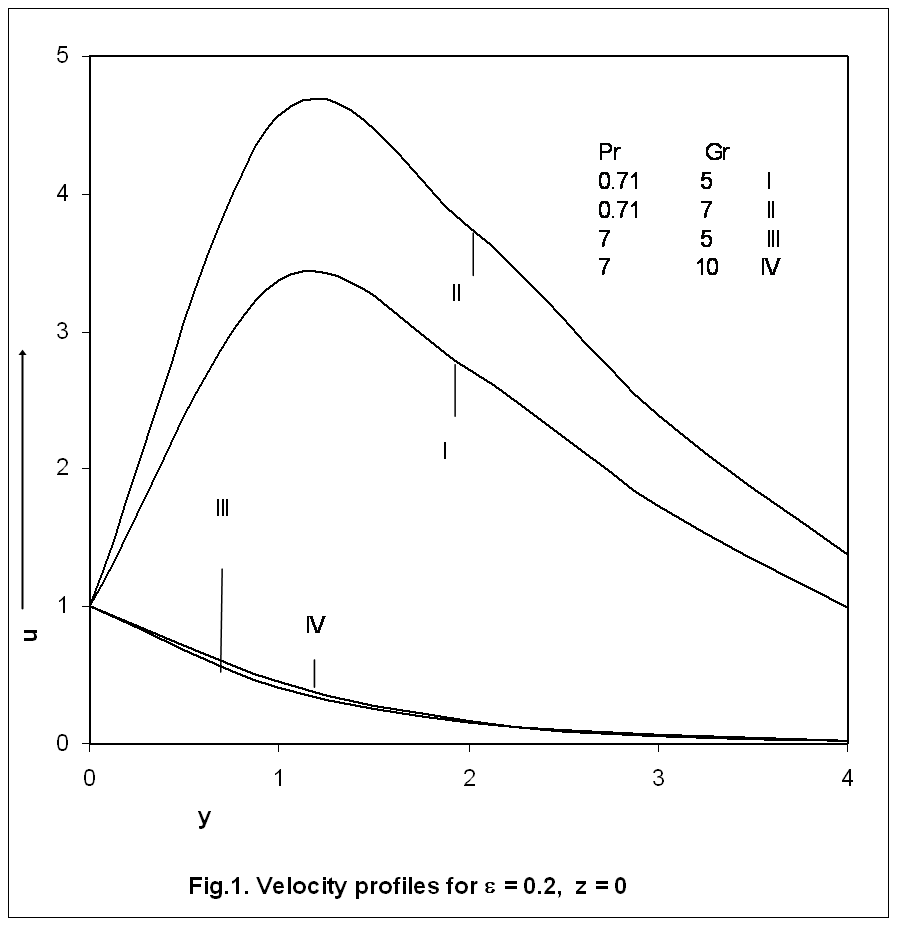 | Figure 1. Velocity profiles for ε = 0.2, z = 0. |
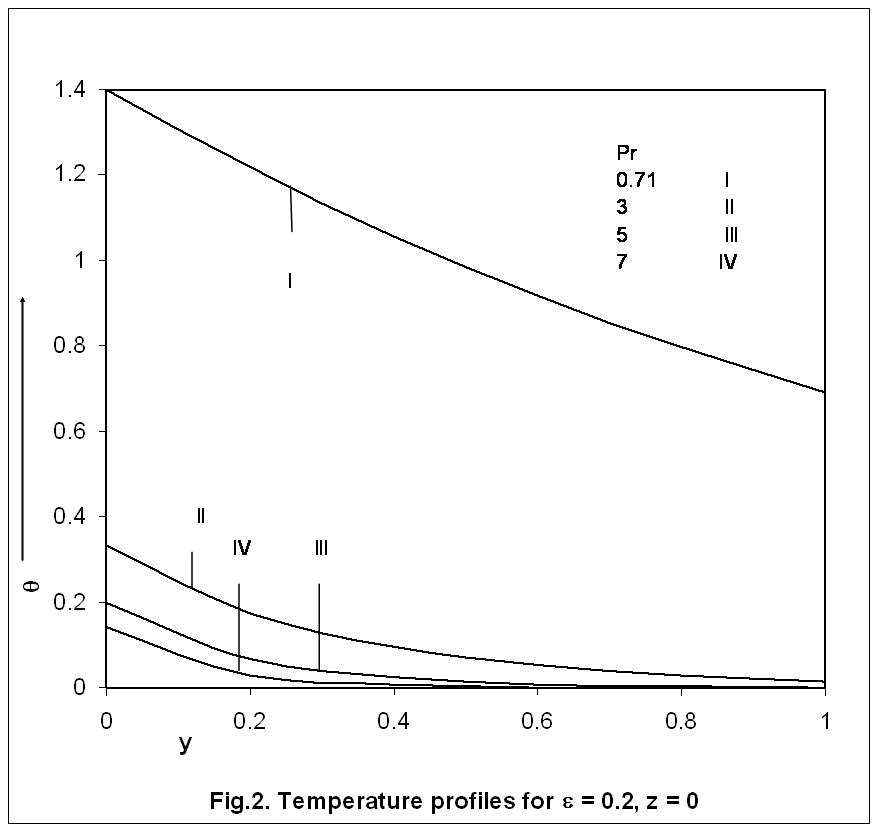 | Figure 2. Temperature profiles for ε = 0.2, z = 0. |
4. Results and Discussion
- Laminar three dimensional mixed convection flow past an infinite vertical porous plate with constant heat flux has been carried out in preceding section. The velocity field, temperature distribution and skin friction coefficient have been obtained and shown in figures for different values of parameters. We now discuss the important flow characteristics of the problem. The values of the Prandtl numbers are chosen as 0.71 and 7.0 approximately, which represent air and water respectively at 200C. The Grashof number Gr takes arbitrary positive values in order to investigate their effects on the flow fields. The velocity profiles are displayed on Figure 1, for various values of Pr (≠ 1) and Gr. It is interesting to note that the velocity increase with increasing Gr, which is true from the physical point of view because of buoyancy increases in the upper direction. In the case of air the fluid velocity increases with increase in Gr, until it attains its maximum value, after which it decreases. The fluid velocity takes its maximum value inside the thermal boundary layer due to the convection currents and as the distance from the vertical plate increases it decays to its limiting value. When Pr = 7, the value of the velocity is very small and approaches to zero as the distance from the surface increases. The variations in Gr do not affect them significantly. An examination of Figure 2 shows that the temperature profiles collapse onto the similar curves as the Prandtl number increases. It is found that the temperature is maximum on the plate and farther from the wall it decays to zero. It is clear from figure that the thermal boundary layer becomes very thin as Pr increases. The physical reason is that the high Prandtl number fluid has a relatively low thermal conductivity which oppose conduction and thereby increase the variations. Thus, results in a reduction in the thermal boundary layer and an increase in the convection heat transfer at wall. From the velocity component u, we can now calculate the skin-friction in the main flow direction in the non-dimensional form as
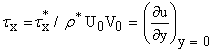 | (46) |
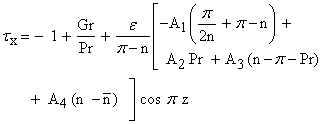 | (47) |
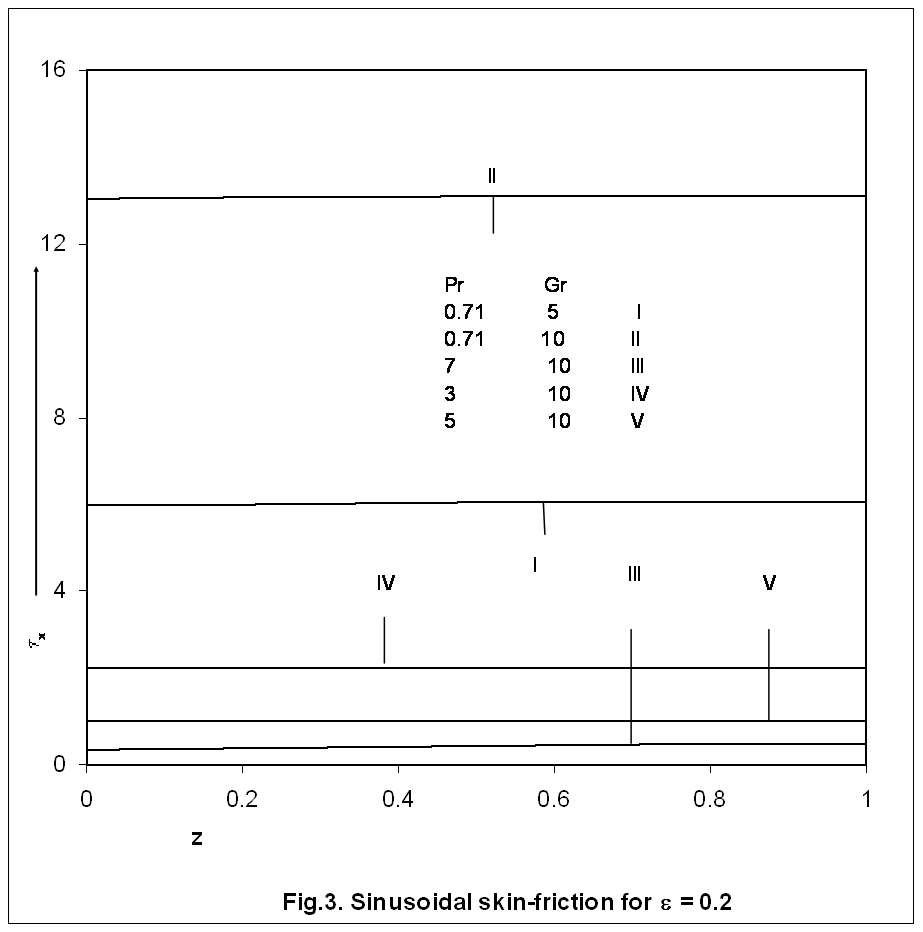 | Figure 3. Sinusoidal skin-friction for ε = 0.2. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML