-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2011; 1(1): 20-26
doi:10.5923/j.ajcam.20110101.05
The Analysis of Hydromagnetic Free Convection Heat and Mass Transfer Flow over a Stretching Vertical Plate with Suction
Y. M. Aiyesimi 1, S. O. Abah 2, G. T. Okedayo 2
1Department of Mathematics, Federal University of Technology, Minna, Nigeria
2Department of Mathematics and Computer Science, Kaduna Polytechnic, Kaduna, Nigeria
Correspondence to: S. O. Abah , Department of Mathematics and Computer Science, Kaduna Polytechnic, Kaduna, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
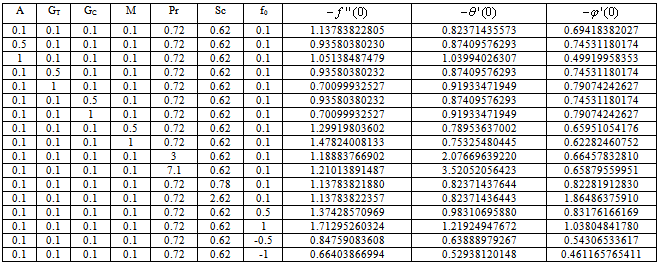
A general analysis has been developed to study the combined effect of the free convective heat and mass transfer on the unsteady two-dimensional boundary layer flow over a stretching vertical plate. The flow is subject to magnetic field normal to the plate. The governing nonlinear partial differential equations have been reduced to the coupled nonlinear ordinary differential equations by the similarity transformations. The resulting equations are solved numerically by using Runge-Kutta the shooting technique. The effects of the Magnetic field Parameter M, buoyancy parameter N, Prandtl number Pr and Schmidt number Sc are examined on the velocity, temperature and concentration profiles. Numerical data for the skin-friction coefficients, Nusselt and Sherwood numbers have been tabulated for various parametric conditions.
Keywords: Hydromagnetic, Free Convection, Suction
Cite this paper: Y. M. Aiyesimi , S. O. Abah , G. T. Okedayo , The Analysis of Hydromagnetic Free Convection Heat and Mass Transfer Flow over a Stretching Vertical Plate with Suction, American Journal of Computational and Applied Mathematics , Vol. 1 No. 1, 2011, pp. 20-26. doi: 10.5923/j.ajcam.20110101.05.
Article Outline
1. Introduction
- The effect of free convection on the accelerated flow of a viscous incompressible fluid past an infinite vertical plate with suction has many important technological applications in the astrophysical, geophysical and engineering problems. The heating of rooms and buildings by the use of radiators is a familiar example of heat transfer by free convection. Heat losses from hot pipes, ovens etc. Heat and mass transfer play an important role in manufacturing industries for the design of fins, steel rolling, nuclear power plants, gas turbines and various propulsion device for aircraft, combustion and furnace design, materials processing, energy utilization, temperature measurements.Most studies have been concerned with constant surface velocity and temperature, but for many practical applications the surface undergoes stretching and cooling or heating that cause surface velocity and temperature variations. Crane (1970), Velggaar (1977), and Gupta (1977) have analyzed the stretching problem with a constant surface temperature, while Soundalgekar and Ramana (1980) have investigated the constant surface velocity case with a power-law temperature variation. Grubka and Bobba (1985) have analyzed the stretching problem for a surface moving with a linear velocity and with a variable surface temperature. The unsteady heat transfer problems over a stretching surface, which is stretched with a velocity that depends on time are considered by Andersson et al. (2000), Elbashbeshy and Bazid (2004) studied the heat transfer over an unsteady stretching surface. Recently, Ishak et al (2007) have studied the heat transfer over an unsteady stretching vertical surface. Ishak et al (2006) have also investigated the unsteady laminar boundary layer over a continuously stretching permeable surface. Ali et al. (1984) studied radiation effect on natural convection flow over a vertical surface in a gray gas. El-Arabawy (2003) studied the effect of suction/injection on a micropolar fluid past a continuously moving plate in the presence of radiation. Ferdows et al. (2004) investigate numerically the thermal radiation interaction with convection in a boundary layer flow at a vertical plate with variable suction. Loganathan (2010) studied the effects of thermal conductivity on unsteady mhd free convective flow over a semi infinite vertical plate.In the above studies the effect of mass transfer over a stretching sheet for a an unsteady problem has been most neglected, therefore, the objective of this study is to investigate numerically using similarity transform together with the Runge-kutta shooting techniques the unsteady heat and mass transfer of a flow over a stretching sheet.
2. Formulation of the Problem
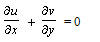 | (1) |
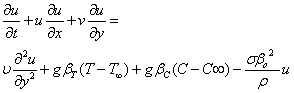 | (2) |
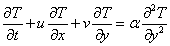 | (3) |
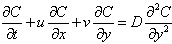 | (4) |
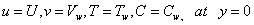 | (5) |
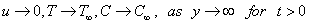 | (6) |
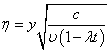 | (7) |
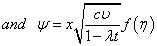 | (8) |
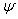 satisfies the equation of continuity, such that
satisfies the equation of continuity, such that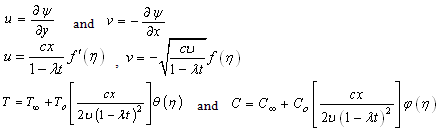 | (9) |
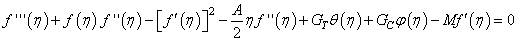 | (10) |
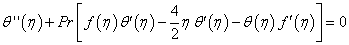 | (11) |
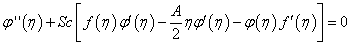 | (12) |
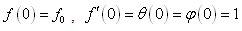 | (13) |
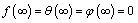 | (14) |
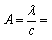 Unsteadiness parameter
Unsteadiness parameter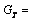 Thermal Grashof number
Thermal Grashof number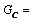 Concentration Grashof numberMagnetic field parameter
Concentration Grashof numberMagnetic field parameter 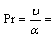 Plandlt number
Plandlt number 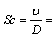 Schmindt number
Schmindt number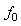 = Suction Parameter
= Suction Parameter3. Numerical Solutions
- The system of non-linear ordinary differential equations (10)–(12) together with the boundary conditions (13) and (14) are locally similar and solved numerically by means of Nachtsheim-Swigert shooting iteration technique along with sixth order Runge-Kutta initial value solver. The numerical results are depicted graphically in Figures 1 to 18 in the form of velocity, temperature and concentration profiles to illustrate the influence of the various physical parameters on the solution.
|
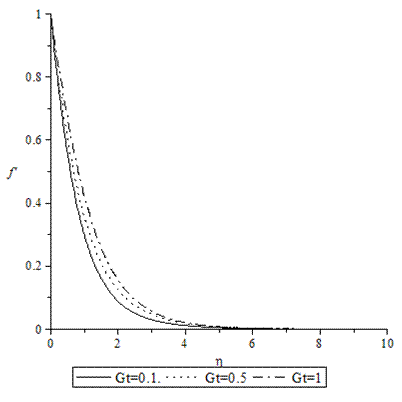 | Figure 1. Velocity profiles for various values of GT when A =M = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
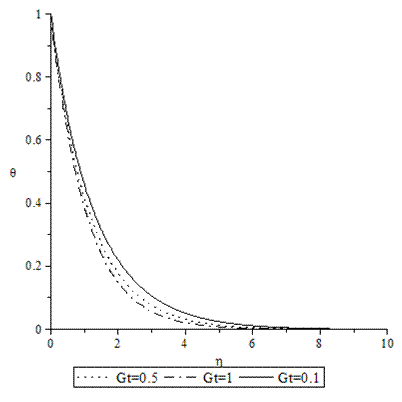 | Figure 2. Temperature profiles for various values of GT when A =M = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
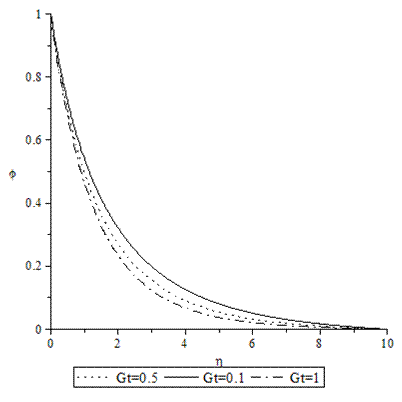 | Figure 3. Concentration profiles for various values of GT when A =M = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
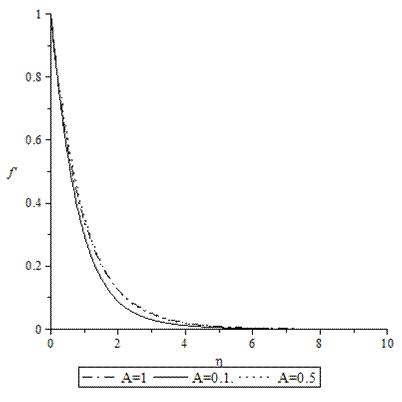 | Figure 4. Velocity profiles for various values of A when M = GT = GC = τ = f0 = 0.1, Sc = 0.62, Pr = 0.72. |
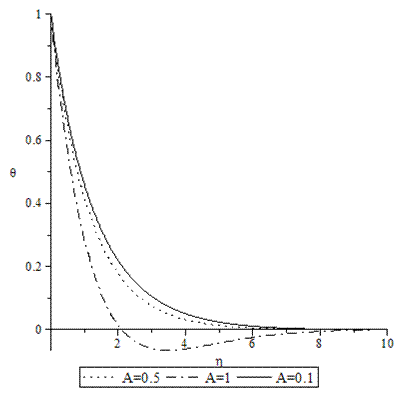 | Figure 5. Temperature profiles for various values of A when M = GT = GC = τ = f0 = 0.1, Sc = 0.62, Pr = 0.72. |
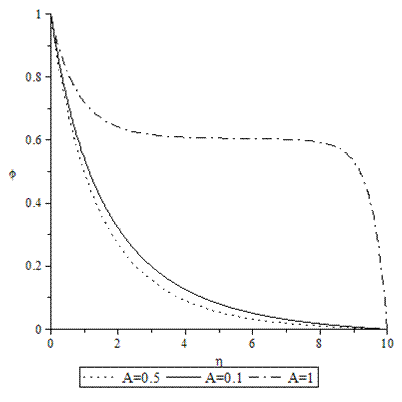 | Figure 6. Concentration profiles for various values of A when M = GT = GC = τ = f0 = 0.1, Sc = 0.62, Pr = 0.72. |
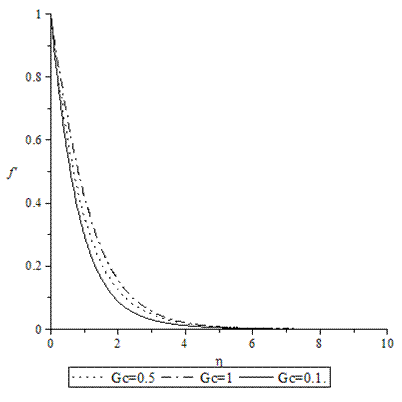 | Figure 7. Velocity profiles for various values of GC when A =M = GT = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
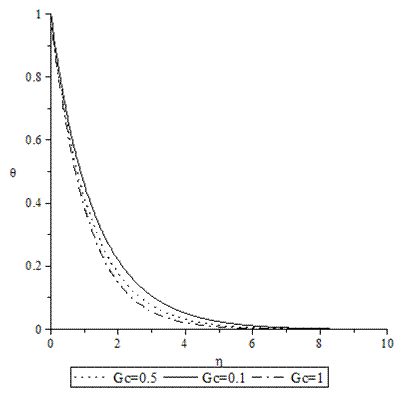 | Figure 8. Temperature profiles for various values of GC when A =M = GT = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
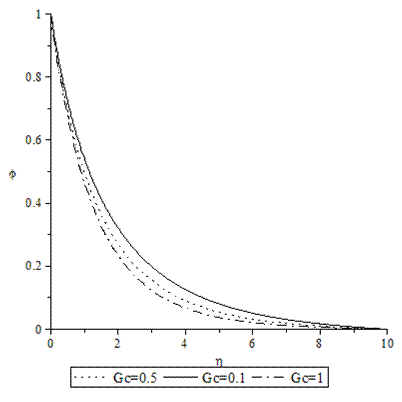 | Figure 9. Concentrations profiles for various values of GC when A =M = GT = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
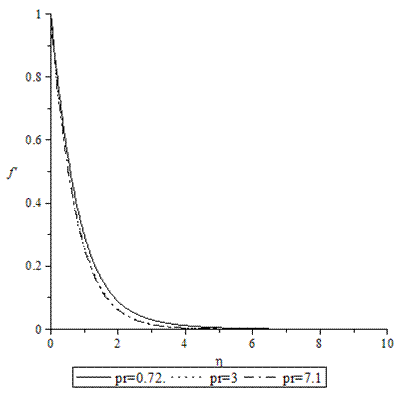 | Figure 10. Velocity profiles for various values of Pr when A =M = GT = GC = τ = f0 = 0.1, Sc = 0.62. |
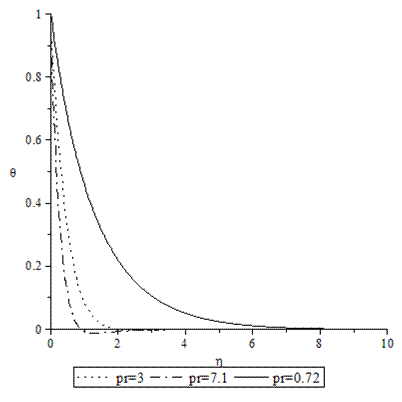 | Figure 11. Temperature profiles for various values of Pr when A =M = GT = GC = τ = f0 = 0.1, Sc = 0.62. |
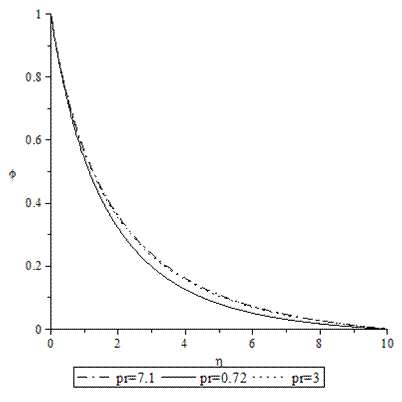 | Figure 12. Concentrations profiles for various values of Pr when A =M = GT = GC = τ = f0 = 0.1, Sc = 0.62. |
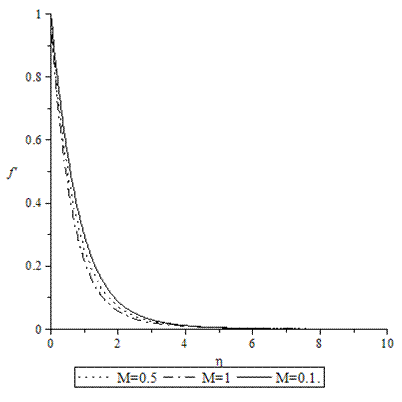 | Figure 13. Velocity profiles for various values of M when A = GT = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
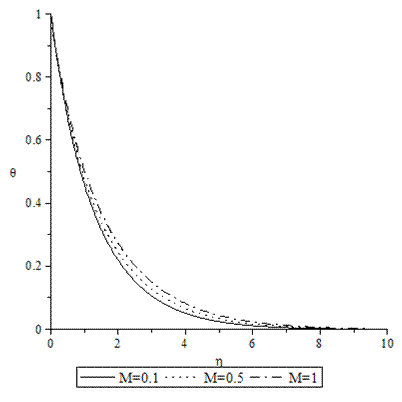 | Figure 14. Temperature profiles for various values of M when A = GT = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
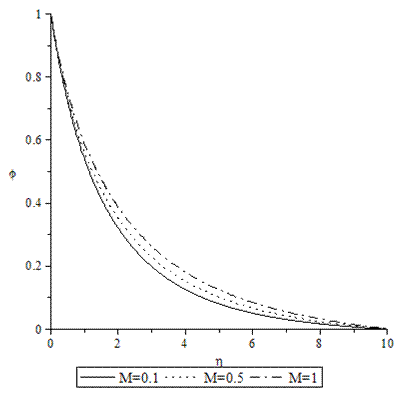 | Figure 15. Concentration profiles for various values of M when A = GT = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. |
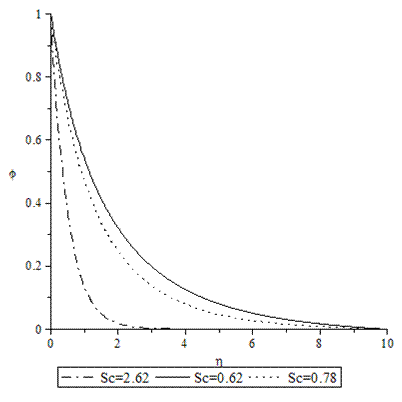 | Figure 16. Concentration profiles for various values of Sc when A =M = GT = GC = τ = f0 = 0.1, Pr = 0.72. |
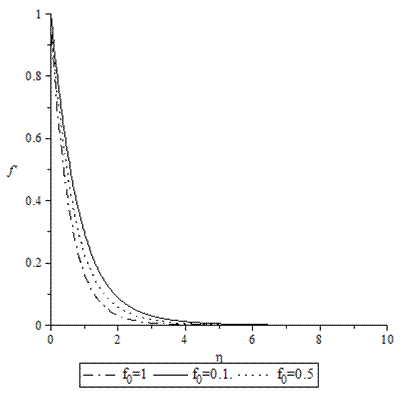 | Figure 17. Velocity profiles for various values of f0 when A =M = GT = GC = τ = 0.1, Pr = 0.72, Sc = 0.62. |
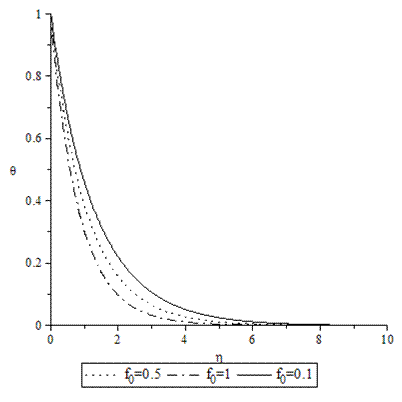 | Figure 18. Temperature profiles for various values of f0 when A =M = GT = GC = τ = 0.1, Pr = 0.72, Sc = 0.62. |
4. Results and Discussion
- Numerical calculations have been carried out for different values of A, GT, GC, M, Pr, Sc and fo, showing the Skin friction, the Nusselt number and the Sherwood number for the various flows embedded by these parameters. Figures 1–3 present typical profiles for the velocity, temperature and concentration for various values of the Thermal Grashof number, GT=0.5, 0.1 and 1, when A =M = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. The velocity profiles for different values of GT, Thermal Grashof number are studied and presented in Figure 1. It is observed that the velocity increases with increasing values of the Thermal Grashof number. In Figure 2, we analyze the effect of Thermal Grashof number (GT) on the temperature of the flow field. A comparison of the curves of the said figure shows that a growing Thermal Grashof number decreases the temperature of the flow field at all points. With the increase of Thermal Grashof number, the molecular motion of the fluid elements is lowered and therefore, the flow field suffers a decrease in temperature at all points. The effect of concentration profiles for different values of GT, Thermal Grashof number is presented in Figure 3. It reveals that concentration decreases with the increase of the Thermal Grashof number.Figures 4–6 shows the profiles for the velocity, temperature and concentration for various values of the unsteadiness parameter, A=0.5, 0.1 and 1, when GT =M = GC = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62. Figure 4, shows that the increase in the unsteadiness parameter leads to an increase in the velocity. From Figure 5, we see that the temperature profiles decreases with the increase of the unsteadiness parameter. In Figure 6, it is observed that the concentration decreases with increasing values of the unsteadiness parameter.The typical profiles for the velocity, temperature and concentration for various values of the Concentration Grashof number, GC=0.5, 0.1 and 1, when A =M = GT = f0 = τ = 0.1, Pr = 0.72, Sc = 0.62, is shown in Figures 7-9. Figure 7 illustrates that the increase in the Concentration Grashof number leads to an increase in the fluid velocity. The effects of the Concentration Grashof number on the temperature and Concentration profiles are shown in Figure 8 and Figure 9 respectively. We found that, both the temperature and Concentration decreases with the increase of the values of the Concentration Grashof number.For different values of Plandlt numbers, Pr=0.72, 3 and 7.1 when A =M = GT = GC=f0 = τ = 0.1, Sc = 0.62, Figures 10-12, presents the velocity, temperature and concentration profiles. From Figure 10, it is clearly seen that the velocity profiles decrease with the increase of the Prandtl number. Physically, this is true because the increase in the Prandtl number is due to increase in the viscosity of the fluid which makes the fluid thick and hence causes a decrease in the velocity of the fluid. The Prandtl number also has decreasing effect on the temperature profiles as shown in Figure 11. Figure 12 depicts the effect of Prandtl number on the concentration of the fluid. It is noticed that an increase in the value of Prandtl number leads to an increase in the concentration distribution across the boundary layer.In Figures 13–15 the profiles for the velocity, temperature and concentration is shown for various values of the Magnetic field parameter. The presence of a magnetic field normal to the flow acts against the flow. This resistive force tends to slow down the flow and hence the fluid velocity decreases with the increase of the magnetic field parameter as observed in Figure 13. From Figure 14, we see that the temperature profiles increase with the increase of the magnetic field parameter, which implies that the applied magnetic field tends to heat the fluid, and thus reduces the heat transfer from the wall. In Figure 15, the effect of an applied magnetic field is found to decrease the concentration profiles, and hence increase the concentration boundary layer.For the case of different values of Schmidt number Sc when A =M = GT = GC = τ = f0 = 0.1, Pr = 0.72, the concentration profiles are presented in Figure 16. The effect of the Schmidt number is dominant in concentration field. It is observed that the concentration decreases with increasing values of the Schmidt number.The variations in fluid Velocity and temperature profiles for various values of the Suction parameter (f0), when A =M = GT = GC = τ = 0.1, Pr = 0.72, Sc = 0.62, are shown in Figures 17 and 18 respectively. From Figure 17, we found that the velocity decreases with the increase of suction parameter. It is also clear that suction stabilizes the boundary layer growth. Figure 18 reveals that temperature decreases with the increase of the suction parameter.
5. Conclusions
- In this paper we have studied numerically the effects on hydromagnetic free convection heat and mass transfer flow over a stretching vertical plate with suction. The particular conclusions drawn from this study can be listed as follows:1. It is found that the velocity increases and temperature and concentration of the fluid decrease with an increase in the thermal and concentration Grashof numbers.2. The velocity and concentration tends to rise as the unsteadiness increases while reverse is the case for the temperature.3. Increasing the Prandtl number decreases the velocity and temperature of the fluid and increases the concentration. The concentration of the fluid decreases with the increase in the Schmidt number.4. In the presence of a magnetic field, the fluid velocity is found to be decreased, associated with a reduction in the velocity gradient at the wall, and thus the local skin-friction coefficient decreases. Also, the applied magnetic field tends to decrease the wall temperature gradient and concentration gradient, which yield a decrease the local Nusselt number and the local Stanton number.5. It was established that an increase in the wall suction enhances the boundary layer thickness and reduces the skin friction.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML