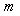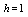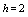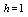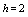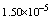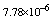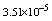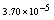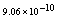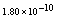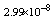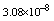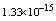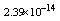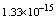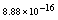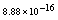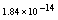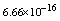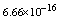-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2011; 1(1): 15-19
doi: 10.5923/j.ajcam.20110101.04
Numerical Solution of Nonlinear Singular Ordinary Differential Equations Arising in Biology Via Operational Matrix of Shifted Legendre Polynomials
K. Maleknejad , E. Hashemizadeh
Department of Mathematics, Karaj Branch, Islamic Azad University, Karaj, Iran
Correspondence to: K. Maleknejad , Department of Mathematics, Karaj Branch, Islamic Azad University, Karaj, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper proposed a numerical method for nonlinear singular ordinary differential equations, that arises in biology and some diseases. We solved these nonlinear problems by a new method based on shifted Legendre polynomials. Operational matrices of derivatives for this function are presented to reduce the nonlinear singular boundary value problems to a system of nonlinear algebraic equations. The method is computationally very simple and attractive, and applications are demonstrated through illustrative examples. The results obtained are compared by the known results.
Keywords: Nonlinear Singular Boundary Value Problem, Legendre Polynomials, Operational Matrix of Derivative, Collocation Method, Biology
Cite this paper: K. Maleknejad , E. Hashemizadeh , "Numerical Solution of Nonlinear Singular Ordinary Differential Equations Arising in Biology Via Operational Matrix of Shifted Legendre Polynomials", American Journal of Computational and Applied Mathematics , Vol. 1 No. 1, 2011, pp. 15-19. doi: 10.5923/j.ajcam.20110101.04.
Article Outline
1. Introduction
- The aim of this paper is to introduce a new method for the numerical solution of the following class of singular boundary value problems
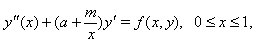 | (1) |
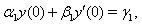 | (2) |
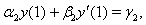 | (3) |
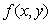 is continuous,
is continuous, 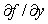 exists and is continuous and also
exists and is continuous and also 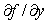
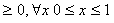 . The boundary value problem (1)-(3) with
. The boundary value problem (1)-(3) with 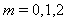 and arise in the study of various tumor growth problems, see ([1-6]), with linear
and arise in the study of various tumor growth problems, see ([1-6]), with linear 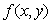 and with nonlinear
and with nonlinear 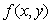 of the form
of the form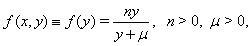 | (4) |
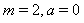 in the study of oxygen diffusion problem in a spherical cell with Michaelis-Menten Kinetics, see ([7-9]). A similar problem arise with
in the study of oxygen diffusion problem in a spherical cell with Michaelis-Menten Kinetics, see ([7-9]). A similar problem arise with 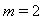 and
and 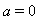 in modelling of heat conduction in human head, see[10-13], with
in modelling of heat conduction in human head, see[10-13], with 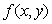 of the form
of the form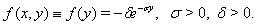 | (5) |
2. Definitions and Properties of Shifted Legendre Polynomials
- Consider the Legendre polynomials
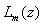 on the interval
on the interval 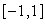
 the set
the set 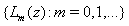 in Hilbert space
in Hilbert space 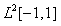 is a complete orthogonal set[22,23]. In order to use these polynomials on the interval
is a complete orthogonal set[22,23]. In order to use these polynomials on the interval 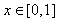 we define the so-called shifted Legendre polynomials by introducing the change of variable
we define the so-called shifted Legendre polynomials by introducing the change of variable 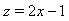 . Let the shifted Legendre polynomials
. Let the shifted Legendre polynomials 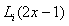 be denoted by
be denoted by 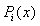 . Then
. Then 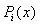 can be obtained as follows:
can be obtained as follows: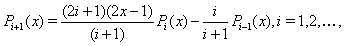 | (6) |
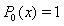 and
and 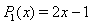 . The analytic form of the shifted Legendre polynomials
. The analytic form of the shifted Legendre polynomials 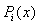 of degree
of degree 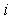 given by
given by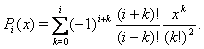 | (7) |
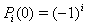 and
and 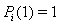 . The orthogonality condition is
. The orthogonality condition is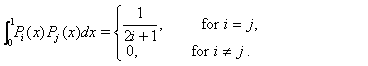 Any function
Any function 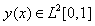 can be expanded in terms of shifted Legendre polynomials as
can be expanded in terms of shifted Legendre polynomials as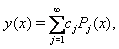 where the coefficients
where the coefficients 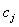 are given by
are given by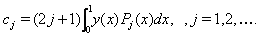 In practice, only the first
In practice, only the first 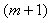 -terms shifted Legendre polynomials are considered. Then we have
-terms shifted Legendre polynomials are considered. Then we have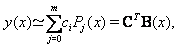 | (9) |
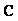 and the shifted Legendre vector
and the shifted Legendre vector 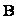 are given by:
are given by: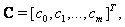 | (10) |
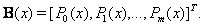 | (11) |
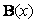 can be expressed by
can be expressed by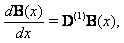 | (12) |
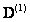 is the
is the 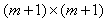 operational matrix of derivative given by[21]
operational matrix of derivative given by[21]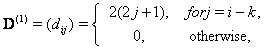 as if
as if 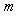 is odd
is odd 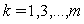 and if
and if 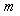 is even
is even 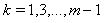 . For example for even we have
. For example for even we have By using Eq. (12), it is clear that
By using Eq. (12), it is clear that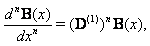 | (13) |
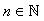 and the superscript, in
and the superscript, in 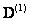 , denote matrix powers. Thus
, denote matrix powers. Thus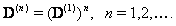 | (14) |
3. Implementation of Shifted Legendre Polynomials Method on Physiology Problems
- In this section we solve nonlinear singular boundary value problem of the form Eq.(1) with the mixed conditions (2) and (3) by using shifted Legendre polynomials.From Eq. (9) we can approximate our unknown as
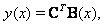 | (15) |
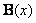 and
and 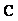 are defined in Eqs.(10) and (11). By using Eqs.(12) and (13) we have
are defined in Eqs.(10) and (11). By using Eqs.(12) and (13) we have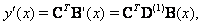 | (16) |
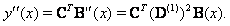 | (17) |
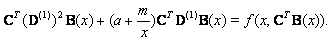 | (18) |
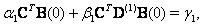 | (19) |
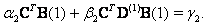 | (20) |
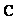 in Eq.(15) is
in Eq.(15) is 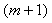 , we collocate Eq.(18) in
, we collocate Eq.(18) in 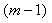 points
points 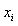 in the interval
in the interval 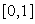 that are roots of shifted Legendre polynomial
that are roots of shifted Legendre polynomial 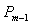 , then we have,
, then we have,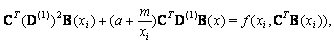 | (21) |
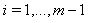 . Now the resulting Eqs. (19), (20) and (21) generate a system of
. Now the resulting Eqs. (19), (20) and (21) generate a system of 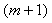 nonlinear equations which can be solved using Newton's iterative method[24,25]. We used the Mathematica 7 software to solve this nonlinear system.
nonlinear equations which can be solved using Newton's iterative method[24,25]. We used the Mathematica 7 software to solve this nonlinear system.4. Illustrative Examples and Applied Models
- To show the efficiency of the proposed numerical method, we implement it on three nonlinear singular boundary problems that arise in real physiology applications. Our results are compared with result in Refs.[17-20]. The austerity of our method in implementation in analogy to other existed methods and its trusty answers is considerable.
4.1. Example 1
- Consider the following oxygen diffusion problem
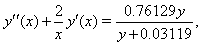 with the boundary conditions:
with the boundary conditions: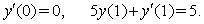 Table 1 shows the numerical results for various number of meshes, and present method solutions are compared with results in Refs.[17] and[18].
Table 1 shows the numerical results for various number of meshes, and present method solutions are compared with results in Refs.[17] and[18].
|
4.2. Example 2
- Consider the following singular two point boundary value problem:
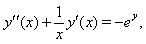
 with the exact solution
with the exact solution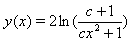 ,where
,where 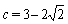 . Table 2 shows numerical errors of this example in analogy to errors for this example in[17].
. Table 2 shows numerical errors of this example in analogy to errors for this example in[17].4.3. Example 3
- Consider this problem that is coincide by heat conduction model of the human head,
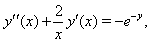 we consider the solution of this problem with conditions as follows:
we consider the solution of this problem with conditions as follows: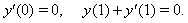 Table 3 illustrates results for this example by proposed method alongside numerical solutions for this example that have been given in Refs[19-20].
Table 3 illustrates results for this example by proposed method alongside numerical solutions for this example that have been given in Refs[19-20].
|
|
|
4.4. Example 4
- Consider the following singular two point boundary value problem:
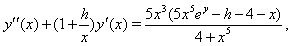 for the following two cases:
for the following two cases: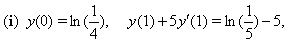
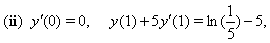 with the exact solution
with the exact solution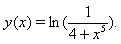 Maximum absolute errors for this problem have been displayed for
Maximum absolute errors for this problem have been displayed for 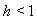 in Table 4 and for
in Table 4 and for 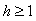 in Table 5, which show the accuracy of proposed method and these results in analogy to exhibited results for this example in[19-20] show advantage of this method.
in Table 5, which show the accuracy of proposed method and these results in analogy to exhibited results for this example in[19-20] show advantage of this method.5. Conclusions
- This paper present a new approach, based on shifted Legendre polynomials for the numerical solution of a class of singular boundary value problems arising in biology and physiology problems. By use of shifted Legendre polynomials as basis and operational matrices of derivatives of these functions we convert such problems to an algebraic system. The implementation of current approach in analogy to existed methods is more convenient and the accuracy is high and we can execute this method in a computer speedy with minimum CPU time used. The numerical applied models that have been presented in the paper and the compared results support our claim.
ACKNOWLEDGEMENTS
- The authors would like to thank Islamic Azad University of Karaj Branch for partially financially supporting this re-search and providing facilities and encouraging this work.
References
| [1] | J.A. Adam, A simplified mathematical model of tumor growth, Math. Biosci., vol.81, pp.224–229, 1986 |
| [2] | J.A. Adam, A mathematical model of tumor growth II: effect of geometry and spatial non-uniformity on stability, Math. Biosci. vol.86, pp.183–211, 1987 |
| [3] | J.A. Adam, S.A. Maggelakis, Mathematical model of tumor growth IV: effect of necrotic core, Math. Biosci., vol. 97, pp. 121–136, 1989 |
| [4] | A.C. Burton, Rate of growth of solid tumor as a prob-lem of diffusion, Growth, vol.30 , pp.157–176, 1966 |
| [5] | H.P. Greenspan, Models for the growth of solid tumor as a problem by diffusion, Stud. Appl. Math., vol.52, pp.317–340, 1972 |
| [6] | N.S. Asaithambi, J.B. Goodman, Point wise bounds for a class of singular diffusion problems in physiology, Appl. Math. Comput., vol. 30 , pp.215–222, 1989 |
| [7] | H.S. Lin, Oxygen diffusion in a spherical cell with non-linear oxygen uptake kinetics, J. Theor. Biol., vol. 60 , pp.449–457, 1976 |
| [8] | D.L.S. McElwain, A re-examination of oxygen diffusion in a spherical cell with MichaelisMenten oxygen uptake kinetics, J. Theor. Biol., vol. 71, pp.255–263, 1978 |
| [9] | N. Rashevsky, Mathematical Biophysics, vol. 1, Dover, New York, 1960 |
| [10] | U. Flesch, The distribution of heat sources in the hu-man head: a theoretical consideration, J. Theor. Biol., vol. 54, pp. 285–287, 1975 |
| [11] | J.B. Garner, R. Shivaji, Diffusion problems with mixed nonlinear boundary condition, J. Math. Anal. Appl., vol. 148, pp. 422–430, 1990 |
| [12] | B.F. Gray, The distribution of heat sources in the hu-man head: a theoretical consideration, J. Theor. Biol., vol. 82 pp. 473–476, 1980 |
| [13] | R.C. Duggan, A.M. Goodman, Point wise bounds for nonlinear heat conduction model for the human head, Bull. Math. Biol., vol. 48 (2), pp. 229–236, 1989 |
| [14] | R.K. Pandy, On a class of weakly regular singular two point boundary value problems II, J, Differential Equa-tions, vol. 127, pp. 110-123, 1996 |
| [15] | M.M. Chawla, P.N. Shivkumar, On the existence of so-lution of a class of singular two--point nonlinear boun-dary value problems, J. Comput. Appl. Math., vol. 19, pp. 379–388, 1987 |
| [16] | R.D. Russell, L.F. Shampine, Numerical methods for singular boundary value problems, SIAM J. Numer. Anal., vol. 12, pp. 13-36, 1975 |
| [17] | S.A. Khuri, A. Sayfy, A novel approach for the solution of a class of singular boundary value problems arising in physiology, J. Math. Comput. Model., vol. 52, pp. 626–636, 2010 |
| [18] | Hikmet Caglar, Nazan Caglar, Mehmet Ozer, B-spline solution of non-linear singular boundary value problems arising in physiology, Chaos Solitons Fractals, vol. 39, pp. 1232-1237, 2009 |
| [19] | J. Rashidinia, R. Mohammadi, R. Jalilian, The numerical solution of non-linear singular boundary value problems arising in physiology, J. Appl. Math. Comput., vol. 185, pp. 360–367, 2007 |
| [20] | R.K. Pandey, Arvind K. Singh, On the convergence of a finite difference method for a class of singular boundary value problems arising in physiology, J. Comput. Appl. Math., vol. 166, pp. 553–564, 2004 |
| [21] | A. Saadatmandi, M. Dehghan, A new operational ma-trix for solving fractional-order differential equations, J. Comput. Math. Appl., vol. 59, pp. 1326–1336, 2010 |
| [22] | K. Maleknejad, B. Basirat, E. Hashemizadeh, Hybrid Le-gendre polynomials and Block-Pulse functions approach for nonlinear Volterra–Fredholm integro-differential eq-uations, Comput. Math. Appl.,vol. 61, pp. 2821–2828, 2011 |
| [23] | K. Maleknejad, E. Hashemizadeh , A numerical approach for Hammerstein integral equations of mixed type using operational matrices of hybrid functions, Scientific Bulle-tin, Series A: Applied Mathematics and Physics, vol. 73(3), pp. 95-104, 2011 |
| [24] | K. Maleknejad, S. Sohrabi, H. Derili, A new computa-tional method for solution of non-linear Volter-ra-Fredholm integro-differential equations, Int. J. Appl. Math., vol. 87(2), pp. 327–338, 2010 |
| [25] | K. Maleknejad, E. Hashemizadeh, B. Basirat, Computational method based on Bernestein operational matrices for nonlinear Volterra-Fredholm-Hammerstein integral equations, Commun. Nonlinear. Sci. Numer. Simulat., vol. 17, pp.52–61, 2012 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML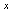
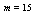
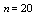
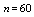
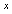
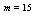
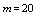
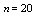
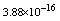
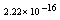
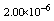
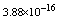
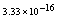
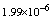
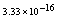
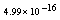
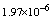
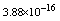
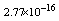
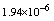
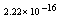
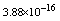
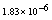
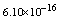
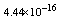
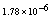
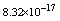
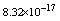
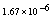
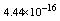
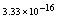
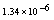
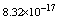
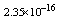
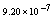
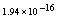
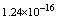
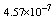
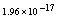
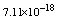
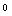
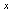
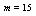
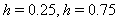 .
.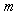
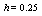
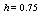
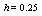
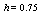
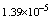
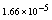
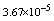
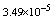
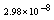
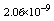
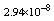
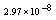
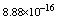
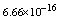
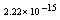
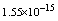
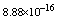
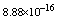
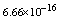
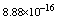
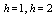 .
.