-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2011; 1(1): 11-14
doi: 10.5923/j.ajcam.20110101.03
Similarity Solutions for Reactive Shock Hydrodynamics
R. Arora
DPT, IIT Roorkee, Saharanpur Campus, Saharanpur, UP-247001, India
Correspondence to: R. Arora , DPT, IIT Roorkee, Saharanpur Campus, Saharanpur, UP-247001, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The method of Lie group invariance is used to obtain a class of self-similar solutions for a one-dimensional, time-dependent problem in shock hydrodynamics, with a chemical reaction taking place behind the shock. The forms of the initial specific volume v0 and the reaction rate Q, for which the problem is invariant and admits self-similar solutions, are also found.
Keywords: Lie Group, Reactive Shock Hydrodynamics, Similarity Solutions, Shock Waves, Invariance, Non-Uniform Medium
Cite this paper: R. Arora , "Similarity Solutions for Reactive Shock Hydrodynamics", American Journal of Computational and Applied Mathematics , Vol. 1 No. 1, 2011, pp. 11-14. doi: 10.5923/j.ajcam.20110101.03.
Article Outline
1. Introduction
- Many flow fields involving wave phenomena are governed by quasi linear hyperbolic system of partial differential equations (PDEs). For nonlinear systems involving discontinuities such as shocks, we do not generally have the complete exact solutions, and we have to rely on some approximate analytical or numerical methods which may be useful to provide information to understand the physics involved. One of the most powerful methods to obtain the similarity solutions to PDEs is similarity method which is based upon the study of their invariance with respect to one parameter Lie group of transformations. Indeed, with the help of infinitesimals and invariant surface conditions, one can construct similarity variables which can reduce these PDEs to ordinary differential equations (ODEs).The physical situation that motivates this study is a hydrodynamic medium in which a chemical reaction occurs. The reaction is initiated by a plane shock wave which is introduced into the medium at time
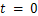 by a driving piston. For detonation waves, it is experimentally observed that after a time, a steady-state condition is reached from the viewpoint of an observer riding on the shock. This problem was first studied by Chapman[1] and Jouget[2], who assumed that the chemical reaction takes place instantaneously in the shock front. Later, their theory was refined by Zeldovich[3], J. Von Neumann[4] and Doering[5], to include a zone of finite width behind the shock, where chemical reaction occurs. A thorough discussion can be found in Courant and Friedrichs[6], and Fickett and Davis[7].Self-similar solutions in non-reactive shock hydrodynamics and gas dynamics have been studied extensively in planar, cylindrical and spherical geometry. We mention thework of Guderley[8], Taylor[9], Sedov[10], Zeldovich and Raizer[11], Sharma and Radha[12], Arora and Sharma [13,14], Sharma and Radha[15] and L. P. Singh et al. [16].In the present paper, following Bluman and Cole[17], Bluman and Kumei[18], and in a spirit closer to Logan[19,20], we obtain the self-similar solutions to a one-dimensional time- dependent problem in shock hydrodynamics with a chemical reaction taking place. Also, we obtain the form of the initial specific volume
by a driving piston. For detonation waves, it is experimentally observed that after a time, a steady-state condition is reached from the viewpoint of an observer riding on the shock. This problem was first studied by Chapman[1] and Jouget[2], who assumed that the chemical reaction takes place instantaneously in the shock front. Later, their theory was refined by Zeldovich[3], J. Von Neumann[4] and Doering[5], to include a zone of finite width behind the shock, where chemical reaction occurs. A thorough discussion can be found in Courant and Friedrichs[6], and Fickett and Davis[7].Self-similar solutions in non-reactive shock hydrodynamics and gas dynamics have been studied extensively in planar, cylindrical and spherical geometry. We mention thework of Guderley[8], Taylor[9], Sedov[10], Zeldovich and Raizer[11], Sharma and Radha[12], Arora and Sharma [13,14], Sharma and Radha[15] and L. P. Singh et al. [16].In the present paper, following Bluman and Cole[17], Bluman and Kumei[18], and in a spirit closer to Logan[19,20], we obtain the self-similar solutions to a one-dimensional time- dependent problem in shock hydrodynamics with a chemical reaction taking place. Also, we obtain the form of the initial specific volume 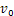 and the reaction rate
and the reaction rate 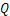 , for which the problem is invariant and admits self-similar solutions.Our attention is directed towards the so-called initiation problem of describing the flow from the initial time when the piston impacts, so the time when a steady-state solution takes effect. In recent years there has been much interest in experimentally measuring the flow parameters (particle velocity, pressure, specific volume, shock velocity etc.) in this regime, and numerical solutions have been extensively developed.
, for which the problem is invariant and admits self-similar solutions.Our attention is directed towards the so-called initiation problem of describing the flow from the initial time when the piston impacts, so the time when a steady-state solution takes effect. In recent years there has been much interest in experimentally measuring the flow parameters (particle velocity, pressure, specific volume, shock velocity etc.) in this regime, and numerical solutions have been extensively developed.2. Formulation of the Model
- We will use a Lagrangian description of the flow, with h denoting the Lagrangian position and
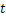 denoting time. Our convention is defined by the equation
denoting time. Our convention is defined by the equation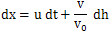 | (1) |
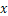 to the Lagrangian position
to the Lagrangian position 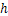 . The quantities
. The quantities 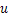 and
and 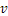 , both functions of t and
, both functions of t and 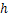 , will denote particle velocity and specific volume, respectively.
, will denote particle velocity and specific volume, respectively.3. Basic Equations and Shock Conditions
- The basic equation can be written as [19,21]:
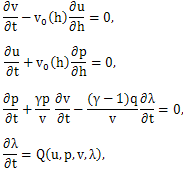 | (2) |
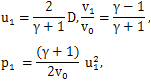 | (3) |
4. Similarity Analysis by Invariance Groups
- In order to obtain the similarity solutions of the system of equations (2) we derive its symmetry group such that the system (2) is invariant under this group of transformations. The idea of the calculation is to find a one-parameter infinitesimal group of transformations (see,[14,15])
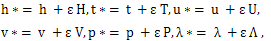 | (4) |
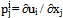 , where i = 1, 2, 3, 4 and j = 1, 2.The system (1), which can be represented as
, where i = 1, 2, 3, 4 and j = 1, 2.The system (1), which can be represented as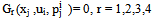 is said to be constantly conformally invariant under the infinitesimal group of transformations 4 if there exist constants αrm
is said to be constantly conformally invariant under the infinitesimal group of transformations 4 if there exist constants αrm 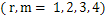 such that
such that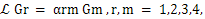 | (5) |
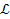 is the extended infinitesimal generator of the group of transformations 4, and is given by
is the extended infinitesimal generator of the group of transformations 4, and is given by | (6) |
 and
and | (7) |
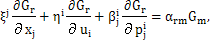 | (8) |
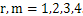 Substitution of
Substitution of  from 7 into 8 yields an identity in
from 7 into 8 yields an identity in 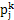 and
and 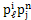 ; hence we equate to zero the coefficients of
; hence we equate to zero the coefficients of  and
and 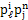 ; to obtain a system of first-order linear partial differential equations in the infinitesimals H, T, U, V, P and Λ. This system, called the system of determining equations of the group of transformations, is solved to find the invariance group of transformations. We apply the above procedure to each equation of the system 1 and R-H conditions, and obtain the system of determining equations in H, T, U, V, P and Λ. We solve this system of determining equations to obtain
; to obtain a system of first-order linear partial differential equations in the infinitesimals H, T, U, V, P and Λ. This system, called the system of determining equations of the group of transformations, is solved to find the invariance group of transformations. We apply the above procedure to each equation of the system 1 and R-H conditions, and obtain the system of determining equations in H, T, U, V, P and Λ. We solve this system of determining equations to obtain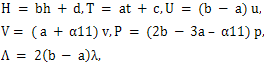 | (9) |
 | (10) |
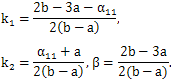 | (11) |
5. Self-Similar Solutions
- We use the invariant surface conditions to determine the similarity variable and the similarity solution. In the present case these conditions for u, p, v and λ, respectively, are
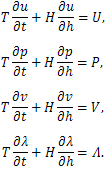 | (12) |
 | (13) |
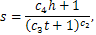 | (14) |
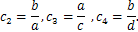 The second first integral gives
The second first integral gives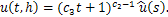 | (15) |
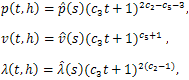 | (16) |
 ,
,  and
and 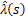 are the functions of the similarity variable s.By substituting the self-similar forms of the solutions u, p, v and
are the functions of the similarity variable s.By substituting the self-similar forms of the solutions u, p, v and 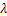 from equation 16 into the system 2 of partial differential equations, we obtain the following system of ordinary differential equations in
from equation 16 into the system 2 of partial differential equations, we obtain the following system of ordinary differential equations in 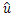 ,
,  ,
, 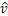 and
and  :
: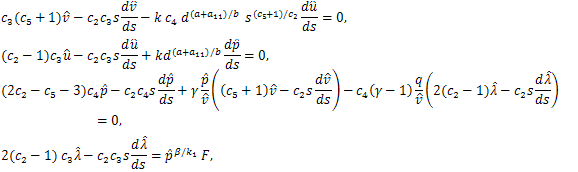 | (17) |
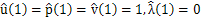 | (18) |
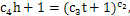 | (19) |
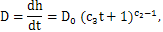 | (20) |
 is the initial shock velocity. The invariance of the jump condition yields the form of the initial specific volume as
is the initial shock velocity. The invariance of the jump condition yields the form of the initial specific volume as | (21) |

6. Conclusions
- We consider the hydrodynamic medium in which a chemical reaction occurs. The reaction is initiated by a plane shock wave which is introduced into the medium at time t = 0 by a driving piston. The method of Lie group invariance is used to obtain a class of self-similar solutions for this problem.The equation 16 provides the forms of the self-similar solutions for u, p, v and λ, respectively. By substituting these self-similar forms of the solutions u, p, v and λ¸ into the system 2 of partial differential equations, we obtain the system 17 of ordinary differential equations in
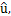
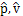 and
and  . This system together with the initial conditions 18 can be solved numerically.The equation (10) provides the form of the reaction rate Q, and the equation (21) yields the form of the initial specific volume v0(h) such that the problem is invariant and admits self-similar solutions. Consequently, it follows that the initial specific volume must satisfy the power law.Also, the shock path is found in the equation (19) and the shock velocity is obtained in the equation (20). For the case of uniform initial specific volume, all these results match well with the solutions obtained in [19].
. This system together with the initial conditions 18 can be solved numerically.The equation (10) provides the form of the reaction rate Q, and the equation (21) yields the form of the initial specific volume v0(h) such that the problem is invariant and admits self-similar solutions. Consequently, it follows that the initial specific volume must satisfy the power law.Also, the shock path is found in the equation (19) and the shock velocity is obtained in the equation (20). For the case of uniform initial specific volume, all these results match well with the solutions obtained in [19].ACKNOWLEDGEMENTS
- Research funding from DST, India vide Project grant number SR/FTP/MS-12/2008 is gratefully acknowledged.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML