K. Ganesan 1, 2, G. Harisha Reddy 2, Sindhura Tokala 2, Raghava Monica Desur 2
1TIFAC-Centre of Relevance and Excellence in Automotive Infotronics, VIT University, Vellore, 632014, India
2School of Information Technology and Engineering, VIT University, Vellore, 632014, India
Correspondence to: K. Ganesan , TIFAC-Centre of Relevance and Excellence in Automotive Infotronics, VIT University, Vellore, 632014, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Programming for multicore processors poses new challenges. The use of multiple cores to increase the processing capabilities of computers is no longer sufficient. In some situations, certain applications may actually run slower on multicore processors than on single core processors. To get the full performance out of multicore chips, their applications need to break tasks into chunks for each core to work on, i.e., parallel computing. Thus, effectively programming for multicore systems so as to increase the speed at which the system performs is very crucial. This takes on a greater level of importance when we are handling complex applications that require high processing power. We take up the task of encrypting video files on a multicore processor. The application captures frames from real time videos and applies scrambling and encryption techniques to securitize them. The scrambling is done in discrete cosine transform domain, discrete Fourier transform domain, and spatial domain. Chaos based cipher block chaining encryption is done to encrypt the video files. The entire process is parallelized over the four cores of a quad-core system.
Keywords:
Video Encryption, Multicore, Scrambling, Cipher Block Chaining, Discrete Cosine Transform, Discrete Fourier Transform, Look-up Table, Chaos
Cite this paper: K. Ganesan , G. Harisha Reddy , Sindhura Tokala , Raghava Monica Desur , Chaos Based Video Security using Multicore Framework, American Journal of Computer Architecture, Vol. 2 No. 1, 2013, pp. 1-7. doi: 10.5923/j.ajca.20130201.01.
1. Introduction
We are living in a digital era. Terry bytes of digital data are generated everyday, in Internet, newspapers, e-mails, mobile phones, etc. Even the cost of hardware devices such as smart phones are tumbling. Almost all cellular phones sold in the market are now fitted with a camera. The wireless networks such as 3G and 4G are becoming ubiquitous. They have enough bandwidth to transmit the real-time video. Hence one has look for simple security algorithms that can transform our data in such a way that only intended recipients alone can use or understand it. The computer industry is at a turning point. Chip manufacturers are shifting away from single processor chips and moving towards a new generation of multiprocessor chips called multicores. Multicore processing is on the rise due to the fact that single core processors are rapidly peaking in their complexity and speed. In the near future, multicore systems are going to become more and more ubiquitous. Application performance can no longer be significantly increased by running unmodified code on processors with more cores. The applications must be coded in order to enable them to be processed in parallel on all the cores. When programming for applications that demand a lot of processing capacity, it becomes all the more vital to ensure that all the system resources are used optimally. Video scrambling and encryption are such applications. Bulk of the video processing so far were confined to a single transform domain. We would like to introduce multiple transform domains to exploit the power of multi cores for video security systems.
2. Problem Definition
Efficient encryption of video data is very crucial for secure transmission in the present day. In various applications like video-conferencing, video surveillance, etc, hiding the video data is necessary to prevent unauthorized personnel from viewing it. Also, in the case of video-on- demand, preventing unauthorized people from accessing the video takes on commercial importance in addition to the security concerns as it is essential that only those who have paid for the services can have access to the video. With the increase in attacks on sensitive data being transmitted, there is a serious need for increasingly complex encryption algorithms. And as the complexity increases, the need to improve the performance by making the most of the processing power available also increases. This need is addressed using parallel programming. The application is parallelized using Intel’s Threading building blocks[1].
3. Parallel Computing
Parallel computing is the form of computation where in the system carries out several operations simultaneously by dividing the problem in hand into smaller chunks, which are processed concurrently. Parallel computing can be accomplished using different classes of computers like Multicore computers, symmetric multiprocessors, cluster computers, massive parallel computers, grid computers, etc.
3.1. Multicore Computers
Multicore systems consist of two or more independent cores on a single integrated circuit die. The cores can also be integrated onto multiple dies on the same chip. To gain the complete advantage of all the cores present in a multicore system, parallelism needs to be incorporated into the algorithm of the software intended for the system. By making the algorithm run parallel on all the cores, significant performance improvements can be gained[2].
3.2. Amdahl’s Law
Amdahl’s law[3] gives the expected speed up of a parallelized implementation of an algorithm when compared to its serial implementation for a constant problem size. If N is the number of processors, s is the amount of time spent (by a serial processor) on serial parts of a program and p is the amount of time spent (by a serial processor) on parts of the program that can be done in parallel, then Amdahl's law says that speedup is given by 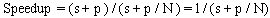 | (1) |
3.3. Gustafson’s Law
Gustafson’s law[4] reevaluates Amdahl’s law. It proposes that parallelism is more useful when we observe that workloads grow as computers become more powerful and support programs that do more work rather than focusing on a fixed workload. For many problems, as the problem size grows, the work required for the parallel part of the problem grows faster than the part that cannot be parallelized. Hence, as the problem size grows, the serial fraction decreases and, according to Amdahl’s law, the scalability improves. According to Gustafson’s Law, the speedup achieved can be formulated as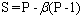 | (2) |
where, P is the number of processors, S is the speed-up, and β the non-parallelizable part of the process.
3.4. Karp-Flatt metric
The Karp-Flatt Metric[2] is a measure of parallelization of code in parallel processor systems. Given a parallel computation exhibiting speedup ψ on p processors, where p > 1, the experimentally determined serial fraction e is defined by the Karp - Flatt Metric as 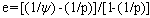 | (3) |
4. Design Methodology
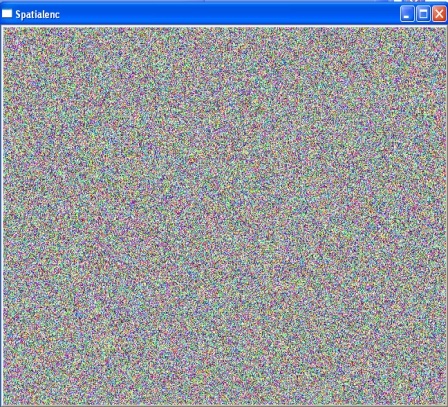
4.1. Video Scrambling in the Spatial Domain
In order to scramble the video in the spatial domain, RBG Image frames are captured from the video. Each one of these frames is a three channel image. The three channel image is split into three single channel images. Each channel is individually scrambled. For each column in a matrix obtained from a single channel image, a random number is generated which is less than the height of the image. The generated random numbers are saved as they are to be used during unscrambling. The random number generated determines the row position about which the pixels are swapped i.e, pixel values above the position of the determined row are swapped with those below the position of the determined row. Each of the scrambled single channel images are merged to obtain a three channel scrambled image. Each such scrambled three channel image is written back to obtain a scrambled video file[5].For unscrambling, image frames are captured from the scrambled video file. Each one of these frames is a three channel image. The image is split into three single channel images. Each scrambled channel is individually unscrambled. For each column in a matrix obtained by single channel image, corresponding random number generated during scrambling is retrieved. The retrieved random number determines the row position (row position=random number generated) about which the pixels are swapped i.e, pixel values above the position of the determined row are swapped with those below the position of the determined row. After unscrambling, R, B, G channels are merged to form three channel original image. Thus, each frame is unscrambled and written back to a video[5].
4.2. Video Scrambling in the Discrete Fourier Transform Domain
Three channel RBG image frames are captured from the video files. For applying the Fourier transform, a complex input (having real and imaginary part) is needed. The captured image frame is split into three single channel images. Each of these single channel images are converted into complex input images by adding a separate channel consisting entirely of zeroes. This zero-channel is considered as the imaginary part. A Discrete Fourier Transform (DFT) is applied to the two channel complex image. After applying the DFT, the complex output is again split into real and imaginary parts. The absolute value is obtained by calculating the magnitude of the complex number[6]. The phase value of each pixel is calculated and stored in a phase matrix. A matrix containing random numbers within the range of (-1.57 ,+1.57), which is the range of the inverse tangent function, is added to the phase matrix of each of the three channels. The sine of phase matrix obtained is merged with the magnitude matrix to obtain a real part and cosine of the phase matrix obtained is merged with the magnitude matrix to obtain an imaginary part. The obtained real and imaginary parts are merged to form a new complex input. The Inverse Discrete Fourier Transform (IDFT) is applied to the new complex input. After applying IDFT the real part obtained is the scrambled image. This process is done for each of the R, G, B channels. The scrambled images obtained in each of the three cases are merged together to give a three channel RBG image, which is the final scrambled output of the Fourier domain scrambling. The frames thus scrambled are written into a video file.To unscramble the video, the scrambled RBG frames are retrieved and each frame is split into the constituent three channels i.e into R, B, G channels. DFT is applied to each individual channel. The phase of the image thus obtained is calculated. The random phase matrix used in the scrambling mechanism is subtracted from this phase matrix. By applying sine and cosine to the phase matrix a new complex input is obtained to which inverse DFT is applied. The image thus obtained is split into its constituent real and imaginary parts. The real part has the unscrambled image for each channel. The unscrambled images from each of the R, B, G channels are combined to get back the original image. Thus, all the scrambled frames are unscrambled and the original video is obtained.
4.3. Video Scrambling in Discrete Cosine Transform Domain
Three channel RBG image frames are captured from the video. The image is split into three single channel images. The Discrete Cosine Transform is applied to each of the channels. A random matrix containing 1 and -1 as elements is generated. This matrix is multiplied with the matrix obtained on applying DCT to the single channel images. It is ensured that the first element of the DCT matrix, which represents the DC coefficient, remains positive. The inverse DCT is applied to the matrix thus obtained. This process is repeated for each of the R, G, B channels. The matrices obtained after applying IDCT to these single channel images are combined to form a three channel image. This image is the output of the DCT domain scrambling, and is written back to get a scrambled video file[7].To unscramble the video, the RBG image frames are extracted and each image is split into the constituent three single channels i.e, into R, B, G channels. DCT is applied to each of R, B, G channels. The matrix obtained after applying DCT is multiplied with the random matrix generated during the scrambling process. IDCT is applied to the matrix thus generated to obtain the unscrambled image for respective channel. The unscrambled images of R, B, G channels are merged to get back the RBG unscrambled image. Thus, the video is unscrambled to get back the original video.
4.4. Cipher Block Chaining Encryption using Chaos
There are many simple nonlinear systems that exhibit sensitivity to initial conditions and their characteristics depends on the parameters of the underlying system. In fact, one can find a large number of such systems in almost every branch of science and engineering[8]. In recent times, many systems have been proposed for encryption purpose. One of the system that has been proposed was to use an 8-dimensional Cat map[9] system. We use this simple system for encrypting videos.
4.4.1. Look-up Table Generation
For implementing the cipher block chaining encryption, a look-up table is needed. For the creation of the look up table an 8-dimensional map (Eqns.4 and 5) is chosen. Initially, eight input values are chosen with each value in the range of (0,1)).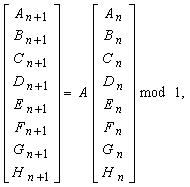 | (4) |
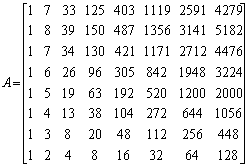 | (5) |
8 initial conditions and A0, B0, C0, D0, E0, F0, G0 and H0 are chosen. By repeatedly applying the function in Eqn.(4), 256 times, eight sequences of 256 unique set of real numbers are obtained[9]. The sequence A (A0, A1, A2,….A255) is sorted and stored in an increasing order in a look up table. Along with each sorted number the iteration in which the number is obtained is stored in the look up table. Also, index values 0 to 255 are stored in this look up table. Now the iteration values and index values stored in the look up table are used for the encryption and decryption process[10].
4.4.2. Cipher Block Chaining Encryption
The three channel RGB image captured from the video is split into three separate channels. For each channel the encryption algorithm is applied. In the encryption algorithm, the value of the first pixel of the channel to be encrypted is obtained and matched against the index values in the look up table. The corresponding iteration value is obtained and the pixel value of the image is replaced by this iteration value. For the subsequent pixels, the pixel value to be encrypted is added to the previous encrypted pixel value and the resultant value mod is taken as shown in Eqn.(6) below: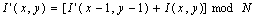 | (6) |
After taking mod, the resultant value is encrypted similar to the first pixel with the help of index and iteration values of the look up table. After encrypting the individual channels, the resultant encrypted images are merged to form the resultant three channel encrypted image, which is written back to obtain the encrypted video.
4.5. Parallelizing the Application
The frames captured from the video are stored in an image array. This array is input into the parallel function. The function divides the data set into chunks of data to be processed in parallel. Each chunk is assigned to a different core, where the security mechanisms are applied to them. The chunk size is decided by experimenting with different values and arriving at the optimal value for each type of partitioner used. The grainsize is initially set to an extremely high value, forcing the system into a single-core behavior. The grainsize is then gradually reduced and the time taken for each run is calculated. When the chunk of image frames arrives at its assigned core, the encryption function takes the image frame number p and computes p% 6. The following Table.1 gives the security mechanism applied, corresponding to the value of p% 6| Table 1. Selection of security mechanisms |
| | p % 6 | Security mechanism | | 0 | Spatial scrambling | | 1 | DFT scrambling | | 2 | DCT scrambling | | 3 | Cipher Block Chaining(CBC) Encryption | | 4 | DFT scrambling + Cipher Block Chaining Encryption | | 5 | DCT scrambling + Cipher Block Chaining Encryption |
|
|
As there are four cores, at any given time during the execution of the program, there are four chunks of image frames being processed. Each core calculates p%6 and assigns the corresponding security mechanism to the frame. Therefore, when the encrypted frames are displayed, they are not in the order they were originally sent in. This further adds to the strength of the security of the system.
5. Results and Conclusions
5.1. Encrypted and Scrambled Video Files
The following image is a snapshot of the video used as an input to the application: | Figure 1. Input Image Frame |
The following Figs.2-7 are the snapshots from videos obtained after applying the securitization mechanisms: | Figure 2. Spatial Scrambled Image |
 | Figure 3. DFT Scrambled Image |
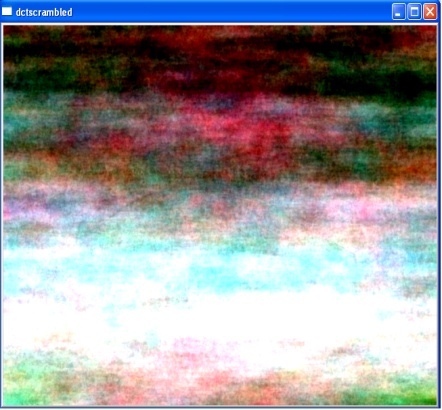 | Figure 4. DCT Scrambled Image |
 | Figure 5. Cipher Block Chaining Encryption |
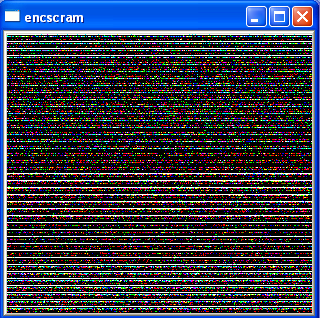 | Figure 6. CBC encryption+ DFT scrambling |
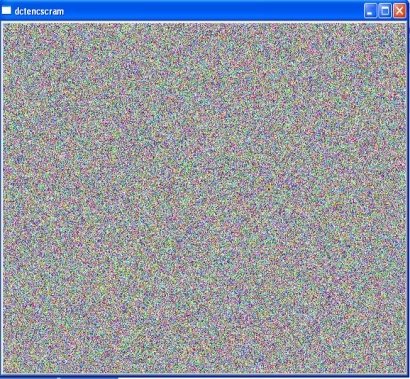 | Figure 7. CBC encryption+ DCT Scrambling |
5.2. Comparative Study of the Performance for Different Grainsizes and Partitioner Mechanisms
Grain size in the Intel Threading Building Blocks[1] specifies the number of iterations for a reasonable sized chunk to assign to a processor core. If the iteration space is greater than the specified grain size, the algorithm splits it into separate sub-ranges that are scheduled separately. Grain size enables us to avoid having extra parallel overhead. There is an overhead cost for every sub-range and therefore, picking a small grainsize may cause excessive overhead. The grainsize is initially set to a significantly high value, so that the application runs only on a single core. It must be reduced subsequently to arrive at a suitable value. The partitioner mechanisms implement rules for deciding when a given range should no longer be subdivided, but should be operated over as a whole by a task’s body. Two different partitioner concepts can be implemented. They are:1. Simple partitioner:It models the default behavior of splitting a range until it can no longer be subdivided.2. Auto partitioner:It models an adaptive partitioner that limits the number of splits needed for load balancing by reacting to work-stealing events.The number of image frames in the video is 20. When the grainsize is fixed as 20 or higher, we are forcing the system into single-core behavior, and hence, the execution time is very high. An immediate drop in the execution time is noticed when the grain size is reduced to lower than the size of the image array. An immediate drop in the execution time is noticed once again when the grain size is reduced to lesser than 10 frames. When the grain size is greater than 10, the initial image array can be divided into a maximum of two chunks. But when it is reduced to lesser than 10, more than two chunks are possible. From the above Table.2, we can observe that the least execution time of 5.448638 seconds is obtained when auto-partitioner is used with a grain size of 1. | Table 2. Execution time corresponding to grain-size |
| | Grain Size | Execution Time for Auto-Partitioner | Execution Time for Simple Partitioner | | 20 | 18.414392 | 18.34634 | | 19 | 10.617401 | 10.43181 | | 18 | 10.521329 | 10.54815 | | 17 | 10.605526 | 10.5497 | | 16 | 10.571234 | 10.4218 | | 15 | 10.635480 | 10.52456 | | 14 | 10.600380 | 10.42627 | | 13 | 10.548144 | 10.43997 | | 12 | 10.516680 | 10.53837 | | 11 | 10.576334 | 10.43293 | | 10 | 10.533820 | 10.45998 | | 9 | 5.8167701 | 5.708027 | | 8 | 5.855042 | 5.751108 | | 7 | 5.84366 | 5.705645 | | 6 | 5.826821 | 5.762026 | | 5 | 5.896711 | 5.735219 | | 4 | 5.92597 | 5.712642 | | 3 | 5.887068 | 5.741831 | | 2 | 5.530374 | 5.496327 | | 1 | 5.448638 | 5.871939 |
|
|
When the same program is run serially, the execution time is found to be 18.53 seconds.
5.3. Speed-up
Speedup is the ratio of the time taken to run a program without parallelism versus the time it runs in parallel. In this case, the speedup achieved is[2]: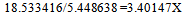 | (7) |
Therefore, the application runs 3.40147 times faster when it is parallelized on the four cores of a multicore system.
5.4. Karp-Flatt metric
The Karp-Flatt Metric[2] is a measure of parallelization of code in parallel processor systems. Given a parallel computation exhibiting speedup ψ on p processors, where p > 1, the experimentally determined serial fraction e defined in Eqn.(3), for ψ = 3.40147 and p = 4 works out to be e = 0.05865. That is, approximately 6 per cent of the program runs in serial, whereas the rest runs in parallel. We know from Amdahl’s law that the speedup of the code is limited by its serial portion. In this application, the serial part is very small when compared to the parallelized part. This means that the code is scalable and the speedup will be greater when the number of cores is increased.
6. Conclusions
Securely transferring the real-time video is considered to be one of the challenging task due to the vast amount of data involved. In the past, only simple scrambling techniques focussed to only a specific transform domain was considered. Most of the works were confined to image processing applications[11]. Recently, many video processing algorithms are proposed that can exploit the power of multi-cores[12]. But thanks to the proliferation of many multi core systems, it is relatively easy to crack such simple scrambled data at the recipient side[13]. To overcome this, it is time to think of scrambling plus encryption techniques[14] to protect the real time data[15]. We have applied simple scrambling techniques in different transform domains such as spatial, DCT and DFT domains. To strengthen our security, we have subsequently encrypted the scrambled data using simple chaos based techniques. The whole process was parallelized using the 4 cores that was available with us.We have considered a real-time video system and scrambled / encrypted different frames of it using different transform domains (such as spatial, DCT and DFT) and various methods discussed in Section 4. The implementation was carried out on a quad core system and we were able to parallelize nearly 94% of our code. As different frames of video are encrypted by different techniques, decrypting the same using conventional brute force technique is very difficult. However, through cryptanalysis part is still in progress.
ACKNOWLEDGEMENTS
The authors of this paper would like to acknowledge the Department of Science and Technology, India for their support and for the financial assistance provided for this work. This work is a part of “Chaos based Security systems in Transform Domains” project funded by DST (Department of Science and Technology) through the grant number:SR/S2/HEP-16/2009 dated 15th Jan 2010. The authors would like to thank the TIFAC-CORE for providing the necessary infra structure facilities to carry out this work successfully.
References
| [1] | J. Reinders, Intel Threading Building Blocks. O’Reilly Media, 2007. |
| [2] | Karp Alan H. and Flatt Horace P. “Measuring Parallel Processor Performance”, Communications of the ACM, Volume 33 Number 5, pp. 549-543, May 1990. |
| [3] | Amdahl, G. "The validity of the single processor approach to achieving large-scale computing capabilities". In Proceedings of AFIPS Spring Joint Computer Conference, Atlantic City, N.J., AFIPS Press, pp. 483–85. April 1967. |
| [4] | John Gustafson, “Reevaluating Amdahl's Law”, Communications of the ACM 31(5), pp. 532–533, 1988. |
| [5] | Frédéric Dufaux and Touradj Ebrahimi. “Scrambling for Video Surveillance with Privacy”. in Proceedings of the 2006 Conference on Computer Vision and Pattern Recognition Workshop, IEEE Computer Society, pp. 160-160, 2006. |
| [6] | S. R. M. Prasanna, Y. V. Subba Rao, and A. Mitra, “An image encryption method with magnitude and phase manipulation using carrier images,” International Journal of Computer Science, vol. 1, no. 2, pp. 131–137, May 2006. |
| [7] | Wenjun Zeng and Shawmin Lei. “Efficient Frequency Domain Selective Scrambling of Digital Video”. IEEE Transactions on Multimedia, Volume 5, issue 1, pp.118 to 129, March 2003. |
| [8] | M. Lakshmanan and S. Rajasekar,” Nonlinear Dynamics, Integrability, Chaos and Spatio-temporal patterns”, Springer- Verlag, (Advanced Texts in Physics) (2003) |
| [9] | K.Ganesan and S. Ganesh Babu, “Chaos based Image encryption using 8D Cat Map (Manuscript in preparation) |
| [10] | Kristina Kelber and Wolfgang Schwarz. “General Design Rules for Chaos-Based Encryption Systems”. In proceedings of the International Symposium on Nonlinear Theory and its Applications 2005 (NOLTA2005) Bruges, Belgium, October 18-21, 2005. |
| [11] | Ying Liu and Fuxiang Gao, “Parallel Implementations of Image Processing Algorithms on Multi-Core”, Fourth International Conference on Genetic and Evolutionary Computing, pp.71-74, 2010. |
| [12] | Zidong Du, Bingbing Xia, Fei Qiao and Huazhong Yang, “System-Level Evluation of Video Processing System Using Simple Scalar Based Multi-Core processor Simulator”, Tenth International Symposium on Autonomous Decentralized Systems”, Washington, pp.256-259, 2011. |
| [13] | Jolly Shah and Vikas Saxena, “Video Encryption: A Survey”, International Journal of Computer Science Issues (IJCSI), Vol.8, Issue 2, pp.525-534, 2011. |
| [14] | M.Abomhara, Omar Zakaria and Othaman O. Khalifa, “An Overview of Video Encryption Techniques”, International Journal of Computer Theory and Engineering, Vol. 2, No. 1, pp.1793-8201, 2010. |
| [15] | Sungju Lee, Eunji Lee, Yongwha Chung, Hyeonjoong Cho and Byoungki Min, “Energy-efficient protection of video surveillance data using multicore-based video sensors”, 6th International Conference on Digital Content, Multimedia Technology and its Applications, pp.327-330, 2010. |

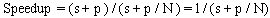
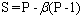
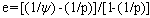


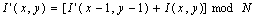







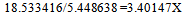
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML