-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computer Architecture
2012; 1(2): 12-20
doi: 10.5923/j.ajca.20120102.01
Architectural Considerations for Compiler-guided Unroll-and-Jam of CUDA Kernels
Apan Qasem
Department of Computer Science, Texas State University, San Marcos, Texas, USA
Correspondence to: Apan Qasem , Department of Computer Science, Texas State University, San Marcos, Texas, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Hundreds of cores per chip and support for fine-grain multithreading have made GPUs a central player in todays HPC world. Much of the responsibility of achieving high performance on these complex systems lies with software like the compiler. This paper describes a compiler-based strategy for automatic and profitable application of the unroll-and-jam transformation to CUDA kernels. The framework supports specification of unroll factors through source-code annotation and also implements a heuristic based on register pressure and occupancy that recommends unroll factors for improved memory performance. We present experimental results on a GE 9800 GT on four CUDA kernels. The results show that the proposed strategy is generally able to select profitable unroll factors. The results also indicate that the selected unroll amounts strike the right balance between register pressure and occupancy.
Keywords: GPU, Compiler Optimization, Memory Hierarchy
Article Outline
1. Introduction
- Increased programmability and inclusion of higher precision arithmetic hardware have catapulted GPUs to the forefront of high-performance computing. Current trends suggest that most (or perhaps all) future high-performance systems will be heterogeneous in nature, consisting of a large collection of general-purpose CPUs and specialized accelerators and GPUs[1]. With hundreds of cores and extremely fine-grain multithreading, GPUs offer massive amounts of on-chip parallelism. Harnessing the raw computational power of the chips still remains a significant challenge, however. Porting of HPC applications to GPUs has required considerable effort in manual tuning[2-6]. Exploiting the architectural resources of these emerging platforms demands sophisticated software tools - specifically optimizing compilers - that analyze and predict a kernel’s interaction with the underlying architecture and automatically restructure code to yield better performance and reduce programmer effort. Although many CPU-centric optimizations can be effective for GPUs, at least in principle, key differences in the architecture and the programming model dictate careful re-evaluation and rethinking of many of these strategies. for some code optimizations this implies a minor adjustment to existing heuristics, whereas for others this might imply a significant departure from the norm.This paper focuses on unroll-and-jam, a well-knownoptimization for exploiting register reuse in CPU-based code[7,8], and investigates the suitability of this optimization for CUDA kernels. We present the requisite safety analysis that enables a compiler to automatically apply this transformation to GPU kernels. We also develop an architecture-sensitive heuristic for selecting profitable unroll amounts. Three main factors make unroll-and-jam an interesting transformation to explore in the context of GPU code optimization:(i) Differences in the register space:Register pressure in the unrolled loop-body is a key consideration for profitable application of unroll-and-jam to CPU codes. If the unroll amount is too large it can increase the register pressure to an extent that causes enough register spills that nullify any gains from exploited data locality. The register space on GPUs is different than its CPU counterpart. Registers on each streaming multiprocessor (SM) are shared by all co-running threads in a thread block and typically there are a large number of registers (thousands) available per SM. Because of fine-grain multithreading, the register demands for a GPU thread is generally substantially lower than CPU threads. This allows the compiler greater freedom in choosing unroll amounts without adversely affecting the memory performance.(ii) Intra vs. inter-thread data locality:Unroll-and-jam aims to improve register reuse by bringing iterations of the outer loop closer together in time. On CPUs, this implies that the compiler need only consider outer-loop carried reuse for profitability. Because GPU codes typically contain threads that perform small tasks (e.g., add and update one array element), often time iterations of both the outer and inner loops will be executed by independent threads. Because memory is shared at various levels on the GPU (global memory by all SMs and shared-memory by thread blocks on an SM), this implies the same memory location can be touched by different threads in a block and thus data reuse can span multiple threads. Therefore, unlike conventional compilers, an optimizing compiler for GPUs needs to account for not only intra-threaddata locality but also inter-thread datalocality.(iii) Occupancy vs. thread granularity:The third issue that makes unroll-and-jam a good optimization to study is the intricate relationship between inter-thread data locality, thread granularity and occupancy that is observed on parallel code running on GPUs. By fusing iterations of the outer loop, the compiler will also affect thread granularity. In particular, as the unroll amount increases, so too will the granularity. Increased granularity will inversely affect the occupancy of the running code, which can degrade performance. Therefore, any heuristic for unroll-and-jam must carefully weigh these factor and choose an unroll amount that strikes the right balance between occupancy and exploited register reuse. The strategy for unroll-and-jam described in this paper addresses the above issues. Our analysis framework accounts for both intra- and inter-thread data locality and attempts to trades-offs register reuse for occupancy. The main contributions of this paper are•A framework to provide compile-time support for both automatic and semi-automatic unroll-and-jam•An architecture-sensitive heuristic for profitable application of unroll-and-jam
2. Relate Work
- Because general-purpose computing on GPUs is a fairly new idea and the technology is still maturing, much of the software based performance improvement strategies have been limited to manual optimization. Ryooet al.[9] present an optimization framework for CUDA kernels that apply several techniques to hide memory latency, and use local memory to alleviate pressure on global memory bandwidth. Govindarajuet al. propose new FFT algorithms for GPUs that are hand optimized to extract impressive good memory performance over CPU-based implementations[5]. The main transformation used in their work is the interleaving of transpose operations with FFT computation. Demmel and Volkov[10] manually optimize the matrix multiplication kernel and produce a variant that is 60% faster than the autotuned version in CUBLAS 1.1. Among the optimization strategies discussed in this work are the use of shorter vectors at program level and the utilization of the register file as the primary on chip storage space. Petit et al. propose a strategy for optimizing data transfer between CPU and GPU[11]. Gunarathneet al. describe optimization strategies for selectively placing data in different memory levels of GPU memory and also rearranging data in memory to achieve improved performance for three OpenCL kernels[12]. Jang et al. present several low-level architecture-sensitive optimization techniques for matrix-multiply and back-projection for medical image reconstruction[6].There has been some work in combining automatic and semi-automatic tuning approaches with GPU code optimization. Murthy et al. have developed a semi-automatic, compile-time approach for identifying suitable unroll factors for selected loops in GPU programs[13]. The framework statically estimates execution cycle count of a given CUDA loop, and uses the information to select optimal unroll factors. Liu et al.[14] propose a GPU adaptive optimization framework (GADAPT) for automatic prediction of near-optimal configuration of parameters that affect GPU performance. They take un-optimized CUDA code as input and traverse an optimization search space to determine optimal parameters to transform the un-optimized input code into optimized CUDA code. Choi et al. present a model-driven framework for automated performance tuning of sparse matrix-vector multiply (SpMV) on systems accelerated by GPU[15]. Their framework yields huge speedups for SpMV for the class of matrices with dense block substructure, such as those arising in finite element method applications. Williams et al. have also applied model-based autotuning techniques to sparse matrix computation that have yielded significant performance gains over CPU-based autotunedkernels[16]. Nukada and Matsuoko also provide a highly optimized 3D-FFT kernel[17]. Work on autotuning general applications on the GPU is somewhat limited. Govindarajuet al. propose autotuning techniques for improving memory performance for some scientific applications[18] and Dattaet al. apply autotuning to optimize stencil kernels for the GPU[19]. The MAGMA project has focused on autotuning dense linear algebra kernels for the GPU, successfully transcending the ATLAS model to achieve as much as a factor of 20 speedup on some kernels[20]. Grauer-Gray and Cavazos present an autotuning strategy for utilizing the register and shared memory space for belief propagation algorithms[21].Automatic approaches to code transformation has been mainly focused on automatically translating C code to efficient parallel CUDA kernels. Baskaranet al. present an automatic code transformation system (PLUTO) that generates parallel CUDA code from sequential C code, for programs with affine references[22]. The performance of the automatically generated CUDA code is close to hand-optimized CUDA code and considerably better than the benchmarks’ performance on a multicore CPU. Lee et al.[23] take a similar approach and develop a compiler framework for automatic translation from OpenMP to CUDA. The system handles both regular and irregular programs, parallelized using OpenMP primitives. Work sharing constructs in OpenMP are translated into distribution of work across threads in CUDA. However, the system does not optimize data access costs for access in global memory and also does not make use of on-chip shared memory. Petit et al. present automatic methods for extracting threads at compile-time[24]. More recently, Sheiet al. have developed a source-level compilation framework for MATLAB that selectively offloads computation for achieving higher performance through coarse-grained parallelism[25].The work presented in this paper distinguishes itself from earlier work in two ways. First the focus here is on automatic compiler methods rather than manual optimization techniques. Second, the approach supports direct optimization of CUDA source rather than C or OpenMP variants.
3. Compiler Guided Unroll-and-Jam
- In this section, we describe the safety analysis for applying unroll-and-jam and describe the main architectural considerations for applying this transformation profitably.
3.1. Notation and Terminology
- We introduce the following notation and terminology to describe our transformation framework

3.2. Dependence Analysis
- We assume that the input to our framework is a CUDA program that is legally parallelized for execution on a GPU. We assume that the code only uses barrier synchronization via syncthreads(). We also make some of the standard assumptions for reuse and dependence analysis. In particular, we assume all array subscript expressions are affine expressions of loop index variables. Given these assumptions we can make the claim that if there are no barrier synchronization primitives in the kernel body then
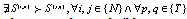 Our dependence analyzer builds on conventional dependence analysis techniques described in the literature[26]. We first build a data dependence graph (DDG) for statements (si) in the body of the kernel. Simple subscript tests are applied to array references to determine if two statements access the same memory location. for CUDA kernels, one issue that complicates the analysis is that memory accesses can be dependent on the value of thread ID. Hence, although a subscript analysis of the source may show two statements as accessing the same memory location, in reality they would access different memory locations. To handle this situation we take the following strategy: we first identify all statements in the kernel that are dependent on thread ID values; expand index expressions to replace subscripts with thread ID values (using scalar renaming[27]) and then apply the subscript test on the expanded expressions. Once all data dependencies have been identified, our dependence analyzer makes another pass through the DDG to identify (control) dependencies that arise from barrier synchronizations. Our primary goal, however, is to discover dependencies between two statement instances, S(i,p)and S(i,q). To test for dependencies in statement instances across threads, we augment the DDG to represent thread and statement instances and maintain data access information across execution of multiple threads.To detect and estimate inter-thread data locality, the analyser needs to consider read-read reuse of data, which may or may not occur between statement instances, regardless of parallel configuration. for this reason, we extend our dependence framework to handle input dependencies. Our framework handles the following two cases of dependence between two statement instances(i) ∃S(i,p)> S(j,q), iffS(i,p)and S(j,q)access the same memory location(ii)∃S(i,p)>S(j,q), iff∃Bksuch that k < jThis final pass through the DDG mainly involves checking for the existence of condition (ii).
Our dependence analyzer builds on conventional dependence analysis techniques described in the literature[26]. We first build a data dependence graph (DDG) for statements (si) in the body of the kernel. Simple subscript tests are applied to array references to determine if two statements access the same memory location. for CUDA kernels, one issue that complicates the analysis is that memory accesses can be dependent on the value of thread ID. Hence, although a subscript analysis of the source may show two statements as accessing the same memory location, in reality they would access different memory locations. To handle this situation we take the following strategy: we first identify all statements in the kernel that are dependent on thread ID values; expand index expressions to replace subscripts with thread ID values (using scalar renaming[27]) and then apply the subscript test on the expanded expressions. Once all data dependencies have been identified, our dependence analyzer makes another pass through the DDG to identify (control) dependencies that arise from barrier synchronizations. Our primary goal, however, is to discover dependencies between two statement instances, S(i,p)and S(i,q). To test for dependencies in statement instances across threads, we augment the DDG to represent thread and statement instances and maintain data access information across execution of multiple threads.To detect and estimate inter-thread data locality, the analyser needs to consider read-read reuse of data, which may or may not occur between statement instances, regardless of parallel configuration. for this reason, we extend our dependence framework to handle input dependencies. Our framework handles the following two cases of dependence between two statement instances(i) ∃S(i,p)> S(j,q), iffS(i,p)and S(j,q)access the same memory location(ii)∃S(i,p)>S(j,q), iff∃Bksuch that k < jThis final pass through the DDG mainly involves checking for the existence of condition (ii).3.3. Safety Analysis
- For simplicity, we only describe the analysis necessary to safely apply unroll-and-jam to the outer dimension of a two-level loop nest. The same principles can be adopted, in a relatively straightforward manner, for unroll-and-jamming loops with more than two levels of nesting.In sequential code, an unroll-and-jam transformation will be illegal if there are dependencies whose direction is reversed as a result of applying the transformation. If a dependence is carried by the outer loop before the transformation but carried by the inner loop after, then such a dependence will prevent the fusing of the outer loop iterations and make unroll-and-jam illegal. for such dependencies, however, the transformation may still be legal if the dependence distance, is less than the unroll factor Ul.To determine the safety of unroll-and-jam for CUDA kernels, where a parallelized loop may be unrolled, we need to translate the safety constraints within statements in a kernel body to statement instances across threads. Let Dube a dependence between two statement instances that prevents a legal unroll-and-jam. Based on our framework, we can derive the following conditions under which Duwill not occur when the unroll factor is Ul.
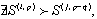 | (1) |
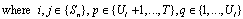 or
or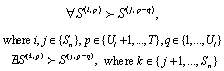 | (2) |
3.4. Profitability
- We consider three factors in selecting profitable unroll amounts: inter-thread data locality, register pressure and thread occupancy. First, we ensure that there is sufficient inter-thread data reuse in the kernel to make unroll-and-jam worthwhile. We then constrain the unroll factor by the estimated register pressure and thread occupancy.
3.4.1. Detecting Inter-thread Locality
- A CUDA kernel exhibits inter-thread data locality if two threads in the same thread block accesses the same location, either in shared memory or global memory. Generally, scalars are allocated to registers within each thread and hence unroll-and-jamming does not help with reuse of such values. Thus, we focus on array references, which are typically not allocated to registers by the compiler. Also, on the Fermi chip, it is possible for two threads to access a memory location that maps to the same cache line. However, we do not explicitly consider the case of spatial reuse in this paper.Given this framework, an array reference in the kernel can only exhibit either self-temporal or group-temporal inter-thread data reuse. Self-temporal reuse can only occur if no subscript in the array reference depends on any of the thread ID variables. If the subscripts are not dependent on thread ID variables it implies that for that reference, all threads in the thread block will access the same memory location. Thus, identifying self-temporal reuse is simply a matter of inspecting each array reference and determining if the subscript values are independent of thread ID values.To compute group-temporal reuse we introduce the notion of thread independent dependence. There is a thread independent dependence between two references if it can be established that there is a dependence between the two references when the entire kernel executes as a single thread (i.e., executes sequentially). The advantage of using thread independent dependencies is that their existence can be determined by using conventional dependence tests. Once group-temporal reuse has been established between two references M1 and M2 in a thread independent way, we determine if the locality translates to inter-thread locality when the task is decomposed into threads. for inter-thread reuse to exist, at least one subscript in either reference has to be dependent on the thread ID value. This implies that although M1 and M2 access the same memory location, the access may occur from two different threads. We formally, define the presence of inter-thread reuse as followsThere is inter-thread data reuse in kernel K if(i) there exists an array reference A with subscripts i0,...,in in K such that no i∈ {i0, . . . , in} is a function of the thread ID value(ii) there exists thread independent dependence between array reference M1 and M2, and at least one subscript in M1 or M2 is an affine function of the thread ID
3.4.2. Estimating Register Pressure
- Although the PTX analyser[29] can provide fairly accurate per-thread register utilization information, because we apply the code transformation on CUDA source, we require a method to estimate register pressure at the source level. To this end, we developed a register pressure estimation algorithm based on the strategy proposed by Carr and Kennedy[30]. Our strategy operates on the source code AST and the DDG built by our framework. The basic idea is to identify references that exhibit register level reuse. If there are multiple references with register level reuse then we predict that the compiler will coalesce them into a single register. We estimate the number of registers needed per thread (Rest) and then constrain it with the number of available registers (Ravail). One limitation of this approach is that it does not consider the possibility of any other transformation being applied to the kernel other than unroll-and-jam. We plan to extend this model in future to address this issue.
3.4.3. Thread Occupancy
- The maximum active warps for each GPU platform is hard-coded into our model. We use the grid configuration to determine the number of active warps for each kernel during compile-time. The ratio of the active warps and the maximum number of warps is then used to compute the occupancy OK for kernel, K. Although studies have shown that it is possible to achieve high performance even at lower occupancy[31], it has also been shown that occupancy below a certain threshold can severely degrade performance of CUDA kernels[32]. We take the conservative approach in our model and use a 50% loss in occupancy as a threshold value. This means, that if, as a result of applying unroll-and-jam, occupancy is reduced from 80% to 40% then we fore-go the transformation.
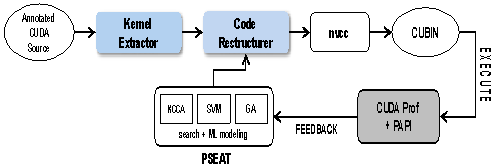 | Figure 1. Overview of transformation framework |
4. Code Transformation Framework
- Figure 1 gives an overview of CREST, our code restructuring and tuning framework for CUDA kernels. The framework leverages several existing tools including nvccfor code generation, HPCToolkit[33] and PAPI[34] for collection of performance metrics, and PSEAT[35] for online search algorithms. The rest of the components have been developed from scratch.
4.1. Kernel Extraction
- To facilitate analysis, a stand-alone Perl script is used to extract the kernel from the CUDA source file before parsing. This simplifies the parser by setting aside everything external to the kernel being analysed. The extraction is performed on a line-by-line basis, using Perl regular expressions to detect the kernel specific portion of the source file. The kernel is extracted into a separate file for further processing and everything else is held in temporary files for later reassembly. The kernel extraction is designed to be independent of the succeeding phases, and could be used in any application where CUDA kernels are to be examined
4.2. Code Restructurer
- At the heart of the framework is a source-to-source code transformation tool that analyses dependencies in CUDA kernels and implements a range of optimizations, some of which, to our knowledge, are currently not supported by any source-to-source transformer or by nvcc. These transformations include scalar replacement, multi-level loop fusion and distribution, loop interchange, and thread coarsening. More specialized transformations such as array padding for eliminating conflicts in cache (on Fermi) and shared memory banks, array contraction for orchestrating placement of data, and iteration space splicing for reducing conditionals in kernels are currently being included in the tool. In addition to providing support for high-level code transformations, the code restructurer also implements several GPU specific heuristics for profitable application of these transformations. for example, when applying tiling on the GPU, the framework selects a tile size (and shape) that aims to improve intra-thread locality and reduce the number of synchronizations.
 | Figure 2. Source-code directives in CREST |
4.3. Autotuning Support
- Autotuning of kernels and applications has emerged as a dominant strategy in the HPC domain. As architectures and applications grow in scale and complexity, the need for autotuning is likely to be even more pronounced. With this picture in mind, we have designed our framework with support for autotuning. Currently, CUDAprof is used to collect performance feedback from CUDA kernel execution. This feedback is sent to a search engine, PSEAT, that implements a variety of online (genetic algorithm, simulated annealing), and offline (support vector machines, kernel component analysis) search methods. Our future plans include developing an interface with PAPI 4.2 to collect better diagnostic feedback to make the tuning process more efficient.
5. Evaluation
5.1. Experimental Setup
- Our primary experimental platform is a Tesla C2050 NVIDIA Fermi GPU. The card has a compute capability of 2.0 and consists of 448 cores divided among 14 multiprocessors. Number of 32-bit registers allocated to each multiprocessor is 32K, while the amount of shared memory available per block is 48KB. Additional experiments are conducted on a GeForce 9800 GT with 112 cores. All CUDA programs are compiled with nvcc version 3.2, and all C programs are compiled with GCC 4.1.2.To evaluate our strategy, we select four kernels that occur frequently in scientific computation. The kernels exhibit varying amounts of outer loop reuse. Since a key focus of our proposed scheme is to consider the effect of unroll-and-jam on inter-thread data locality, we specifically use CUDA implementations where the loop being unrolled has been parallelized. Table 1 provides a brief description of each benchmark.
5.2. Performance Improvement
- Figure 3 shows performance improvements yielded by our unroll-and-jam strategy on both GPU platforms. In each case only one outer loop is unrolled and the heuristic described in Section 3.4.3. The speedups reported are over the baseline version where no unrolling is performed. The best performance improvement on both platforms is seen for stencil. This is not surprising since stencil exhibits the most inter-thread reuse with nine shared references in three arrays. Among the four kernels, mm shows the least improvement (we provide some explanation about this poor-showing in Section 5.3.4).Overall, the strategy yields more benefits on the Fermi board than the GeForce. We speculate this performance difference may be attributed to cache effects, although we have not explored that issue in this paper.
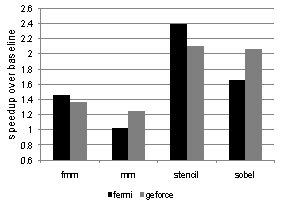 | Figure 3. Performance improvement via compiler-guided unroll-and-jam |
5.3. Post-mortem Analysis
- The overall performance numbers only tell a partial story about the interaction of unrolled loops with different parts of the GPU memory hierarchy. To get a clearer picture, we ran a series of experiments to isolate the effects of unroll amounts on different aspects of performance. We discuss these results next.
5.3.1. Performance Sensitivity
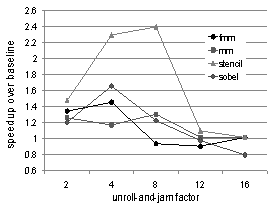 | Figure 4. Performance sensitivity of CUDA kernels to unroll amounts on the Fermi board |
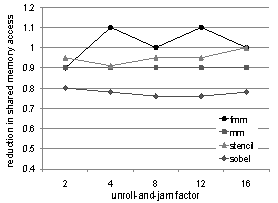 | Figure 5. Effect of unroll-and-jam on global memory access |
5.3.2. Memory Access
- To further investigate the fluctuations in the performance curves, we measure, for each kernel, number of loads and stores to different levels of the memory hierarchy. Figures 5 and 6 show the reduction in normalized global and shared memory access counts. We observe that some of the variations in performance are indeed explained by these charts. There is reasonable correlation between the number of shared-memory accesses reduced and achieved performance. It appears there is little variation in global memory access for different unroll amounts. These flatter curves for global memory access fit our expectations, since most of the data reuse in the selected kernels occur in arrays, allocated to shared memory.
5.3.3. Scalar Replacement
- We notice in Figure 6 that the reduction in shared memory accesses for sobel flattens out after unroll factor of 4. Although our heuristic chooses 4as the optimal unroll factor because of the occupancy constraint, we were curious as to why there was not a larger reduction in shared memory access for unroll factors >4. On closer inspection of the resulting assembly code, we discovered that for sobel, nvcc was not allocating several of the array references to registers, resulting in less desirable shared memory behavior. To remedy this situation we applied scalar replacement[8] to the code, which resulted in significant reduction in shared memory access and enabled us to obtain an 18% performance improvement for sobel on Fermi, over the speedup reported in Figure 3. Thus, sobel serves as a good example where scalar replacement needs to be used in tandem with unroll-and-jam (a la CPU) to achieve better register reuse.
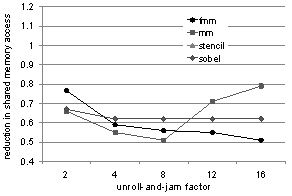 | Figure 6. Effect of unroll-and-jam on shared memory access |
5.3.4. Shared Memory Conflicts
- The speedup obtained from mm is relatively lower than the speedup obtained on the other kernels. This result is counter-intuitive because the shared-memory accesses actually increase for unroll factors greater than 8. To explore this situation further, we used to decuda to disassemble the code generated by nvcc and inspected the assembly code. We discovered that the generated kernel code contained many pointer references to shared memory, which possibly resulted in shared memory bank conflicts. Although we are unclear as to why this type code was generated, we discovered that similar findings on matrix-multiply had been reported earlier by Volkovet al.[31]. This situation can be averted by transposing the matrix. However, our framework does not currently support automatic matrix transpose and we leave this as future enhancement for our framework.
5.3.5. Register Pressure
- We also measure number of local memory accesses for each kernel for different unroll amounts. These measurements were taken to get a sense of the number register spills suffered by a kernel. Somewhat surprisingly, we found no significant change in number of accesses to local memory on either platform even for very high unroll amounts. These results suggest that excessive register pressure may not be as big a threat to unroll-and-jam as originally suspected.
6. Conclusions and Future Work
- This paper describes a compiler-based strategy for applying unroll-and-jam to CUDA kernels. We present an architecture-aware heuristic for profitable selection of unroll amounts. Preliminary evaluation suggests that the scheme is effective in finding unroll factors that is able to exploit reuse at the shared-memory level without exceeding the register pressure or causing a significant drop in occupancy. Experimental results indicate that register pressure is a less important consideration than occupancy when applying unroll-and-jam to CUDA kernels.The experimental results also revealed several aspects of the GPU architecture that needs to be accounted for when applying unroll-and-jam to CUDA kernels including the need for applying scalar replacement in unrolled loops and avoiding shared-memory pointer access. Our future work will involve enhancing our unroll-and-jam strategy to take these factors into account. As part of future work, we also plan to extend our analysis framework to apply unroll-and-jam to multiple loops in a nest.
Notes
1We realize this is a simplifying assumption. We plan to incorporate warp-levellock-step synchronizationandfence synchronization in future.
References
| [1] | J. Dongarra and P. e. a. Beckman, “The International Exascale Software Roadmap,” International Journal of High Performance Computer Applications, vol. 25, no. 1, 2011. |
| [2] | K. Z. Ibrahim, F. Bodin, and O. P`ene, “Fine-Grained Parallelization Of Lattice Qcd Kernel Routine On GPUs,” J. Parallel Distrib. Comput., vol. 68, October 2008. |
| [3] | A. Rahimian, I. Lashuk, S. Veerapaneni, A. Chandramowlishwaran, D. Malhotra, L. Moon, R. Sampath, A. Shringarpure, J. Vetter, R. Vuduc, D. Zorin, and G. Biros, “Petascale Direct Numerical Simulation Of Blood Flow On 200k Cores and Heterogeneous Architectures,” in Proceedings of the 2010 ACM/IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, 2010. |
| [4] | Y. Zhuo, X-L. Wu, J. P. Haldar, W.-m. Hwu, Z.-p. Liang, and B. P. Sutton, “Accelerating Iterative Field-Compensated MR Image Reconstruction on GPUs,” in Proceedings of the 2010 IEEE international conference on Biomedical imaging: from Nano to Macro, ser. ISBI’10, 2010. |
| [5] | N. K. Govindaraju, B. Lloyd, Y. Dotsenko, B. Smith, and J. Manferdelli, “High Performance Discrete Fourier Transforms On Graphics Processors,” in SC ’08: Proceedings of the 2008 ACM/IEEE conference on Supercomputing. Piscataway, NJ, USA: IEEE Press, 2008, pp. 1–12. |
| [6] | B. Jang, S. Do, H. Pien, and D. Kaeli, “Architecture-Aware Optimization Targeting Multithreaded Stream Computing,” in Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units, 2009. |
| [7] | M. Lam, E. Rothberg, and M. E. Wolf, “The Cache Performance and Optimizations Of Blocked Algorithms,” inProceedings of the Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS-IV), Santa Clara, CA, Apr. 1991. |
| [8] | D. Callahan, S. Carr, and K. Kennedy, “Improving Register Allocation for Subscripted Variables,” in Proceedings of the SIGPLAN ’90 Conference on Programming Language Design and Implementation, White Plains, NY, Jun. 1990. |
| [9] | S. Ryoo, C. I. Rodrigues, S. S. Baghsorkhi, S. S. Stone, D. B. Kirk, and W.-m. W. Hwu, “Optimization Principles and Application Performance Evaluation of a Multithreaded GPU Using CUDA,” in Proceedings of the 13th ACM SIGPLAN Symposium on Principles and practice of parallel programming, 2008. |
| [10] | V. Volkov and J. W. Demmel, “Benchmarking GPUs To Tune Dense Linear Algebra,” in SC ’08: Proceedings of the 2008 ACM/IEEE conference on Supercomputing, 2008. |
| [11] | R. D. E. Petit, F. Bodin, “An Hybrid Data Transfer Optimization for GPU,” in Compilers for Parallel Computers (CPC2007), 2007. |
| [12] | B. Salpitikorala, A. Chauhan, and G. Fox, “Optimizing OpenCL Kernels for Iterative Statistical Algorithms on GPUs,” in In Proceedings of the Second International Workshop on GPUs and Scientific Applications (GPUScA), 2011. |
| [13] | M. B. G. Murthy, M. Ravishankar and P. Sadayappan, “Optimal Loop Unrolling for GPGPU Programs,” in IEEE International Symposium on Parallel Distributed Processing, 2010. |
| [14] | L. Yixun, E. Z. Zhang, and X. Shen, “A Cross-Input Adaptive Framework for GPU Program Optimizations,” in Proceedings of the 2009 IEEE International Symposium on Parallel and Distributed Processing, 2009. |
| [15] | J. W. Choi, A. Singh, and R. W. Vuduc, “Model-Driven Autotuning Of Sparse Matrix-Vector Multiply On GPUs,” in PPoPP ’10: Proceedings of the 15th ACM SIGPLAN symposium on Principles and practice of parallel programming. New York, NY, USA: ACM, 2010, pp. 115–126. |
| [16] | S. Williams, L. Oliker, R. Vuduc, J. Shalf, K. Yelick, and J. Demmel, “Optimization Of Sparse Matrix-Vector Multiplication on Emerging Multicore Platforms,” Parallel Computers, vol. 35, no. 3, pp. 178–194, 2009. |
| [17] | A. Nukada and S. Matsuoka, “Autotuning 3-D FFT Library for CUDA GPUs,” in SC ’09: Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis. New York, NY, USA: ACM, 2009, pp. 1–10. |
| [18] | N. K. Govindaraju, S. Larsen, J. Gray, and D. Manocha, “A Memory Model for Scientific Algorithms On Graphics Processors,” in SC ’06: Proceedings of the 2006 ACM/IEEE conference on Supercomputing. New York, NY, USA: ACM, 2006, p. 89. |
| [19] | K. Datta, M. Murphy, V. Volkov, S. Williams, J. Carter, L. Oliker, D. Patterson, J. Shalf, and K. Yelick, “Stencil Computation Optimization and Auto-Tuning On State-Of-The-Art Multicore Architectures,” in SC ’08: Proceedings of the 2008 ACM/IEEE conference on Supercomputing. Piscataway, NJ, USA: IEEE Press, 2008, pp. 1–12. |
| [20] | R. Nath, S. Tomov, and J. Dongarra, “Accelerating GPU Kernels for Dense Linear Algebra,” In Proceedings of 9th International Meeting on High Performance Computing for Computational Science (VECPAR’10), 2010. |
| [21] | S. Grauer-Gray and J. Cavazos, “Optimizing and Autotuning Belief Propagation On The GPU,” in Proceedings of the 23rd international conference on Languages and compilers for parallel computing, ser. LCPC’10, 2011, pp. 121–135. |
| [22] | M. M. Baskaran, J. Ramanujam, and P. Sadayappan, “Automatic C-To-CUDA Code Generation for Affine Programs.” in Lecture Notes in Computer Science, R. Gupta, Ed., vol. 6011. Springer, 2010, pp. 244–263. |
| [23] | S. Lee, S.-J. Min, and R. Eigenmann, “OpenMP To GPGPU: A Compiler Framework for Automatic Translation and Optimization,” in Proceedings of the 14th ACM SIGPLAN symposium on Principles and practice of parallel programming, 2009. |
| [24] | E. Petit, F. Bodin, G. Papaure, and F. Dru, “Astex: A Hot Path Based Thread Extractor for Distributed Memory System on a Chip,” in Proceedings of the 2006 ACM/IEEE conference on Supercomputing, 2006. |
| [25] | C. -Y. Shei, P. Ratnalikar, and A. Chauhan, “Automating GPU Computing in Matlab,” in Proceedings of the international conference on Supercomputing, ICS11, 2011. |
| [26] | R. Allen and K. Kennedy, “Optimizing Compilers for Modern Architectures”, Morgan Kaufmann, 2002. |
| [27] | R. Cytron and J. Ferrante, “What’s In A Name? -Or- The Value Of Renaming for Parallelism Detection and Storage Allocation”, in ICPP’87, 1987, pp. 19–27. |
| [28] | P. Briggs and K. D. Cooper, “Effective Partial Redundancy Elimination,” in Proceedings of the ACM SIGPLAN 1994 conference on Programming language design and implementation, ser. PLDI ’94, 1994. |
| [29] | “CUDA PTX ISA,” http://www.nvidia.com |
| [30] | S. Carr and K. Kennedy, “Improving The Ratio Of Memory Operations To Floating-Point Operations In Loops,” ACM Transactions on Programming Languages and Systems, vol. 16, no. 6, pp. 1768–1810, 1994. |
| [31] | V. Volkov, “Better Performance At Lower Occupancy,” Supercomputing Tutorial, 2010. |
| [32] | CUDA Programming Guide, Version 3.0. NVIDIA, http://www.nvidia.com, 2010 |
| [33] | L. Adhianto, S. Banerjee, M. Fagan, M. Krentel, G. Marin, J. Mellor-Crummey, and N. R. Tallent, “HPCtoolkit: Tools for Performance Analysis Of Optimized Parallel Programs,” Concurrency and Computation: Practice and Experience, To Appear, 2009. |
| [34] | S. Browne, J. Dongarra, N. Garner, K. London, and P. Mucci, “A Scalable Cross-Platform Infrastructure for Application Performance Tuning Using Hardware Counters,” in Supercomputing, ACM/IEEE 2000 Conference, Nov. 2000. |
| [35] | Q. Yi and A. Qasem, “Exploring The Optimization Space Of Dense Linear Algebra Kernels,” in Languages and compilers for parallel computing, LCPC08, Aug. 2008. |
| [36] | “Stencilprobe: A Microbenchmark for Stencil Applications.” http://www.cs.berkeley.edu/skamil/ |
| [37] | A. Chandramowlishwaran, S. Williams, L. Oliker, I. Lashuk, G. Biros, and R. Vuduc, “Optimizing and Tuning The Fast Multipole Method for State-Of-The-Art Multicore Architectures,” in IEEE International Symposium on Parallel Distributed Processing (IPDPS), 2010. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML