B. T. Krishna
Department of Electronics and Communication Engineering, University College of Engineering Kakinada, Jawaharlal Nehru Technological University Kakinada, Kakinada, Andhra Pradesh, India
Correspondence to: B. T. Krishna, Department of Electronics and Communication Engineering, University College of Engineering Kakinada, Jawaharlal Nehru Technological University Kakinada, Kakinada, Andhra Pradesh, India.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Detection of QRS complex is an important step for the analysis of heart rate variability. It has been proved that the algorithms based on the use of differentiation are proven to be efficient and hence can be used for the real-time analysis. At the same time, fractional order digital differentiators are gaining their interest in many areas of research. In this paper, an attempt is made to detect QRS complex by making use of the proposed transfer functions. The results have been proven to be comparable to the conventional techniques.
Keywords:
Electrode, Fractional Order, Discretization, Slope, Repolarization
Cite this paper: B. T. Krishna, QRS Detection Using Fractional Order Digital Differentiators, American Journal of Biomedical Engineering, Vol. 9 No. 1, 2019, pp. 1-4. doi: 10.5923/j.ajbe.20190901.01.
1. Introduction
Electro cardio Gram signal is an acronym of the ECG Signal. It consists of mainly P, QRS, T and U waves as its constituent parts [1]. This is recorded by placing electrodes on the skin. In general 12 lead techniques is followed to record ECG Signal. There are three main components to an ECG: the P wave, which represents the depolarization of the atria; the QRS complex, which represents the depolarization of the ventricles; and the repolarization of the ventricles is represented by T wave. Each of the components has its own significance in the diagnosis of health of a person. In general, concentration will be paid about the detection of the QRS complex.QRS detection is a widely used technique to identify the function of the heart [1]. Out of many of the existing procedures Pan-Tompkins method is widely used one. This experiment used to identify QRS complexes based on slope, amplitude and width [3]. A novel simple and efficient method for QRS detection in Electrocardiogram (ECG) is proposed in [5]. The data is preprocessed using median filter QRS complex is identified by taking a variable window size. This method is tested in MIT database. QRS detection algorithm, based on adaptive filtering principle, has been presented in [6]. In this paper, many of the LMS algorithm family is compared for the QRS detection and it is observed that Leaky LMS is best. In [7], a novel technique for QRS detection with minimum pre-processing is proposed. The technique uses two-stage median filter and Savitzky–Golay smoothing filter for pre-processing. The results show the robustness of QRS complex detection, which is useful to the accurate cardiac health prognosis. By making use of Shannon energy envelope estimator a R peak detector is proposed in [8]. In [9], a detailed comparative analysis is carried out about different techniques used in the QRS detection. The procedures have been tested on the public data bases that are available, and the values of the sensitivity are also calculated for the comparison.Digital differentiator forms an essential component in the Pan-Tompkins method [2]. Design of fractional order digital differentiators and integrators is an attractive area of research. Recently these devices are playing vital role in many areas of applications. These devices find applications in control, signal and image processing, and other allied fields. Numerous procedures exist for the design of these differentiators and integrators. A lot of literature is also available in the application of these devices to many fields of Engineering. But very few amount of work is done in the application towards bio-medical engineering. In this paper, an attempt is made to use the indirect discretization based fractional order differentiators for the detection of QRS complex. The method is then tested on the MIT/BIH database. The results prove the efficacy of the proposed methodology.The paper is organized as follows. Design of fractional order digital differentiators is discussed in Section 2. QRS detection using the proposed method is discussed in Section 3. Finally results and conclusions are presented in Section 4.
2. Design of Fractional Order Digital Differentiators
A fractional order digital differentiator is defined by the transfer function,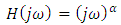 | (1) |
Where α is a fractional order [4]. The design of these devices can be of direct discretization type or indirect discretization type. In the direct discretization, a transform which converts from s domain to z domain will be expanded directly using power series or any other expansion for the design of the fractional order device. The expansion which is of infinite in order will be terminated based on the interest of the designer. In case of indirect discretization initially in s domain itself a rational approximation will be calculated. Then the transforms are used to convert to the digital domain. Both these discretizations have their own advantages and disadvantages. A survey on such techniques is available in [4]. In this paper, fractional order differentiator is designed using indirect discretization scheme. The continued fraction expansion for 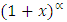 is given in [4] as
is given in [4] as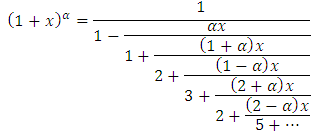 | (2) |
By expanding upto two and four terms the rational approximations for α=0.5 will be,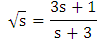 | (3) |
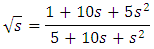 | (4) |
The equations for the Bilinear and Al-Alaoui Transform are given as,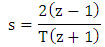 | (5) |
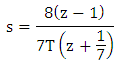 | (6) |
by substituting the s to z transforms in the above rational approximations the differentiators derived will be as given below. For the bilinear case,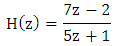 | (7) |
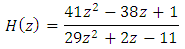 | (8) |
For Al-Alaoui case,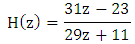 | (9) |
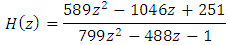 | (10) |
Eqns. (7)-(10) represent the equations for the fractional order differentiators for α=0.5, with first, second order approximations. The four filters are proved to be stable. The higher order approximation is also possible but keeping in view of the hardware complexity, it is restricted only to 2. These equations are used for the QRS complex detection in the coming sections.
3. QRS Detection Using Proposed Fractional Order Digital Differentiators
A typical ECG signal is as shown Fig.1. The Pan Tompkins algorithm used in this paper is as shown in Fig.2. In the First a band-pass filter is present to reduce noise. Then a derivative filter is used to find the value of slope. This is followed by a squaring circuit followed by a moving- window integrator. Then thresholding is done. The bandpass filter is a combination of Lowpass ans high pass filters. The low pass filter is given by the transfer function,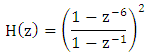 | (11) |
The expression for the High pass filter will be,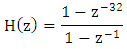 | (12) |
The differentiator used in this conventional method is given by the transfer function,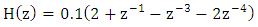 | (13) |
The output of the Eqn. (13) is passed through the moving integrator circuit. Then two types of thresholding is done. The original ECG signal used from physionet database is as shown in Fig.3. Fig.4. is the output of the conventional Pan-Tompkins algorithm. The output with the proposed fractional differentiators is shown in Figs. 5-8.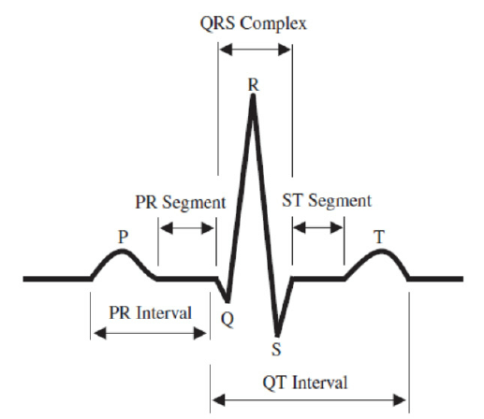 | Figure 1. Typical ECG signal |
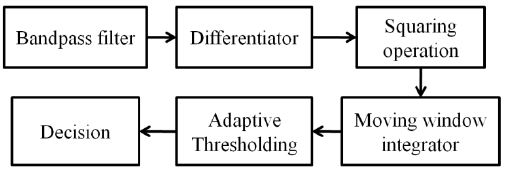 | Figure 2. Pan-Tompkins QRS detection method |
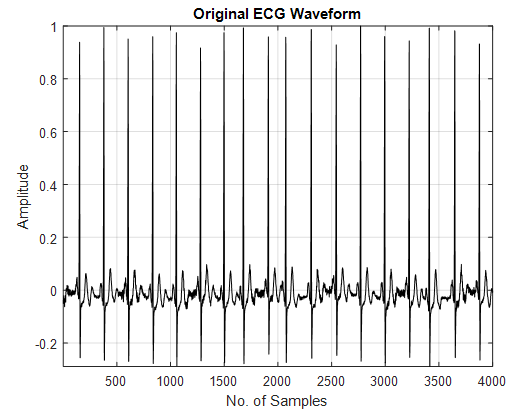 | Figure 3. Original ECG Signal |
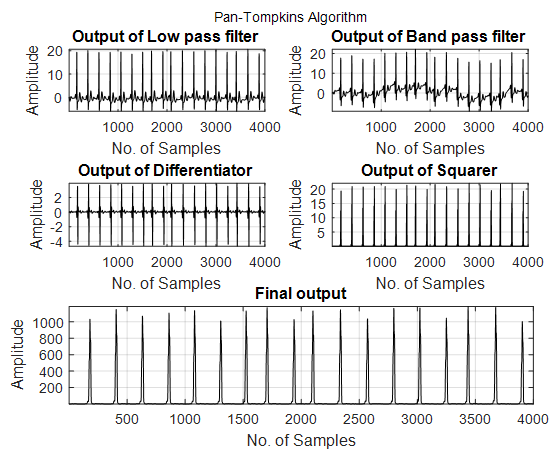 | Figure 4. Output of Original pan Tompkins algorithm |
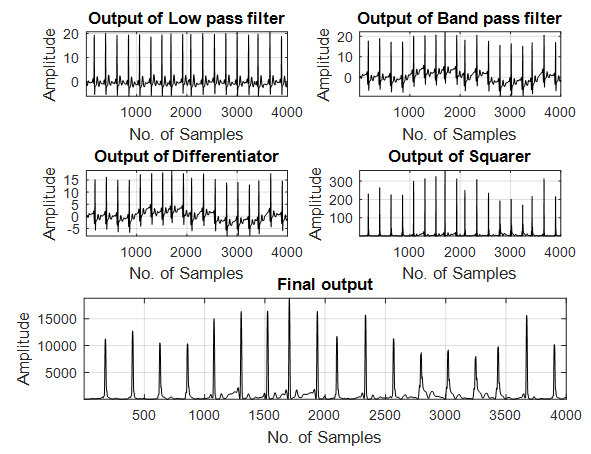 | Figure 5. Outputs with Fractional Bilinear First order case |
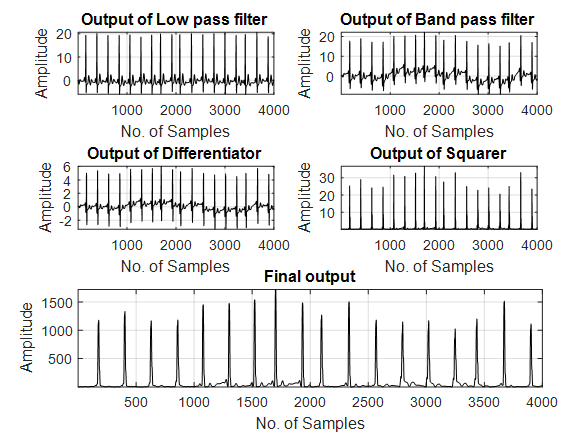 | Figure 6. Output with Fractional Alalaoui first order case |
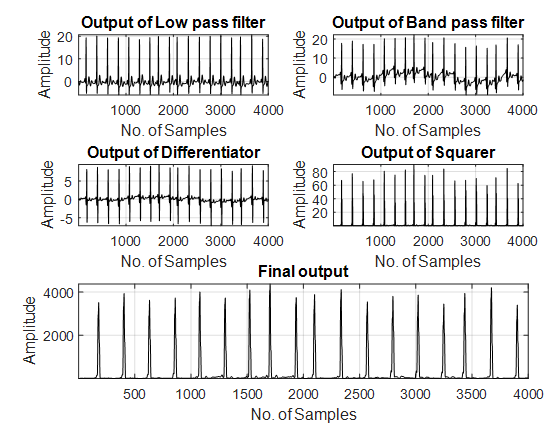 | Figure 7. Output with Second order bilinear fractional case |
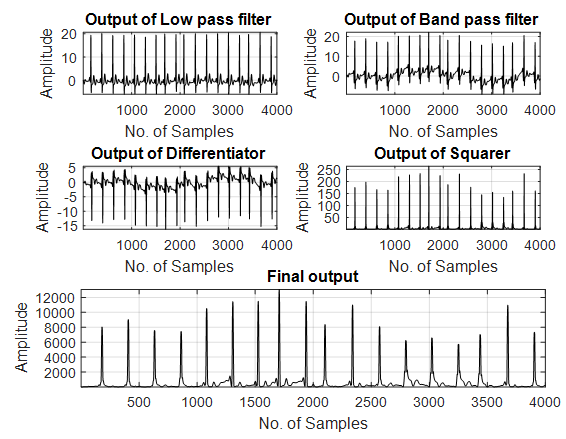 | Figure 8. Output with Second order fractional alalaoui case |
4. Conclusions
A QRS detection using the novel fractional order digital differentiators is proposed in this paper. The detection of QRS complexes can be used to check the health condition of the human being. The differentiator used in the conventional method has been replaced with the proposed differentiator. These differentiators are obtained by the indirect discretization of the bilinear and Al-Alaoui Transforms. The results show that the amplitude of the QRS complex is increased as compared to the conventional case. The peaks detected with the conventional case and the proposed case seems to be similar to each other with a change in amplitude levels. The proposed methods have shown some extra small peaks in the output side. The hardware complexity is also not increased with the proposed case. So, the proposed transfer functions can be used for the detection of the QRS complexes. Thus fractional order digital differentiators are utilised for the QRS complex detection.
ACKNOWLEDGEMENTS
This work was supported by grants from the University Grants Commission (UGC), Bahadurshah Zafar Marg, New Delhi, India, No.F.30-1/2014/RA-2014-16-SC-ANP-5036 (SA-II) dated 20-02-2015. This work is carried out at Jawaharlal Nehru Technological University Kakinada (JNTUK), Kakinada, Andhra Pradesh, India. The Authors wish to acknowledge Vice-Chancellor, Registrar and other Administrative team of Jawaharlal Nehru Technological University Kakinada for providing facilities to carry out this work. The Authors also wish to acknowledge Principal, University College of Engineering (A), Jawaharlal Nehru technological University Kakinada for his encouragement and support.
References
| [1] | W.J. Tompkins, Biomedical Digital Signal Processing, Englewood Cliffs NJ Prentice Hall, 1993. |
| [2] | B.T. Krishna, QRS detection using digital differentiators, International Conference on Electrical Engineering and Informatics (ICEEI), 2015, pp.1-4. |
| [3] | J. Pan, W.J. Tompkins, “A real-time QRS detection algorithm”, IEEE Transactions on Biomedical Engineering, vol. 32, no. 3, pp. 230-236, March. 1985. |
| [4] | B.T. Krishna, “Studies on fractional order differentiators and integrators: A survey”, Signal Processing, vol. 91, no. 3, pp. 386-426, 2011. |
| [5] | A.K. Dohare, V. Kumar, R. Kumar, “An efficient new method for the detection of QRS in electrocardiogram”, Computers in Electrical Engineering, vol.40, pp.1717–1730, 2014. |
| [6] | S. Jain, M.K. Ahirwal, A. Kumar, V. Bajaj, G.K. Singh, “QRS detection using adaptive filters: A comparative study”, ISA Transactions, vol.66, pp.362–375, 2017. |
| [7] | L.D. Sharma, R.K. Sunkaria, “A robust QRS detection using novel pre-processing techniques and kurtosis based enhanced efficiency”, Measurement Journal, vol.87, pp.194–204, 2016. |
| [8] | M.S. Manikandan, K.P. Soman, “A novel method for detecting R-peaks in electrocardiogram (ECG) signal”, Biomedical Signal Processing and Control, vol.7, pp.118–128, 2012. |
| [9] | Raúl Alonso Álvareza, Arturo J. Méndez Penína, X. Antón Vila Sobrinoa, A comparison of three QRS detection algorithms over a public database, Procedia Technology, vol.9, 2013, pp.1159-1165. |



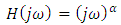
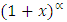 is given in [4] as
is given in [4] as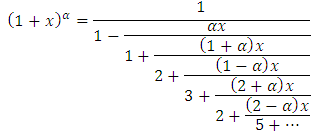
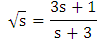
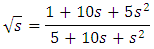
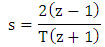
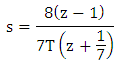
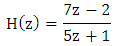
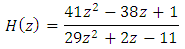
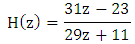
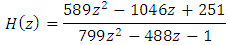
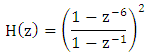
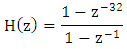
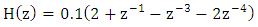








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML