-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Biomedical Engineering
p-ISSN: 2163-1050 e-ISSN: 2163-1077
2015; 5(3): 86-93
doi:10.5923/j.ajbe.20150503.02
A Three-Dimensional Finite Element Model to Study Dynamic Changes of Tissue during Laser Interstitial Thermotherapy
Mohammad Ehsan Salavati, Mohammad Hossein Miran Baygi
Faculty of Electrical and Computer Engineering, Tarbiat Modares University, Tehran, Iran
Correspondence to: Mohammad Ehsan Salavati, Faculty of Electrical and Computer Engineering, Tarbiat Modares University, Tehran, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Laser Interstitial Thermotherapy (LITT) is a surgical method for treatment of cancer in biological tissues such as liver, brain, prostate and neck. Mathematical modeling of the processes in laser-tissue interactions during laser irradiation is essential for optimal treatment planning. One of the parameters that affect the temperature and damage increase in the tissue during LITT is dynamic changes of tissue properties. In this study, a three-dimensional model was developed to model the effect of dynamic changes of tissue properties. Monte Carlo method was used for modeling the light transport in tissue. Finite Element method was used for solving Pennes and Arrhenius equations to obtain distribution of temperature and thermal damage in tissue respectively. Three conditions were considered in this study. The results show that with constant tissue properties the highest temperature and the largest damage volume occur. The temperature increase and damage volume are larger when considering dynamic changes of all properties rather than blood perfusion rate only.
Keywords: Laser Interstitial Thermotherapy, Dynamic Changes, Finite Element Method, Monte Carlo Method, Laser-Tissue Interactions
Cite this paper: Mohammad Ehsan Salavati, Mohammad Hossein Miran Baygi, A Three-Dimensional Finite Element Model to Study Dynamic Changes of Tissue during Laser Interstitial Thermotherapy, American Journal of Biomedical Engineering, Vol. 5 No. 3, 2015, pp. 86-93. doi: 10.5923/j.ajbe.20150503.02.
Article Outline
1. Introduction
- Treatment of cancer has become one of the top priorities in health care centers worldwide and a large amount of resources are invested to improve or find new therapeutic methods for the treatment of cancer. One of the promising and alternative methods of therapy is laser-induced interstitial thermotherapy (LITT). LITT is a minimally invasive treatment to cause hyperthermia and coagulation in tumours in solid organs such as liver, brain, prostate, neck, etc. [1]. LITT treatment is usually performed by inserting a laser applicator into the tumour as shown in Figure 1. The tumour is destroyed by the immediate or delayed hyperthemic and coagulative effects, due to photon absorption and heat transfer in the tissue [2, 3].
 | Figure 1. General Diagram of LITT treatment |
2. Methodology
- For simplicity, in this study we have used a three-layer cubic model. The tumour is the layer between two healthy tissue layers. The laser applicator is placed horizontally in the middle of the tumour layer along x-axis. The geometry of this model is shown in Figure 2. Each layer has the length and width of 4.5 cm and the height of 1.5 cm. So the model is a cube of 4.5*4.5*4.5 cm3.
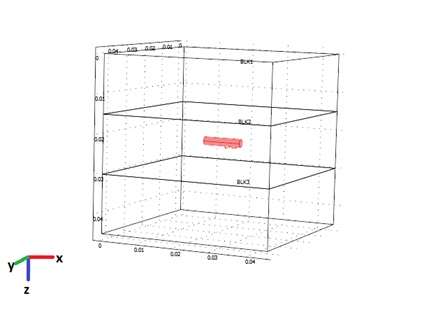 | Figure 2. Geometry of the 3D model |
2.1. Monte Carlo Simulation of Photon Propagation in Tissues
- In biological tissues, light is both absorbed and scattered. Monte Carlo simulation of photon propagation offers a flexible and accurate approach toward photon transport in turbid materials, such as biological tissues; and it can easily deal with two or three dimensional problems with complex geometry [13].Propagation steps in Monte Carlo are either fixed or variable [14-16]. Once the photon is launched, it may be scattered, absorbed, propagated undisturbed, internally reflected or transmitted out of tissue. The photon is repeatedly moved until it escapes from the tissue or it is totally absorbed. If the photon escapes from the tissue, the refection or transmission of the photon is recorded. If the photon is absorbed, the position of the absorption is recorded. Once this has been done a new photon is launched at the origin. This process is repeated until the desired numbers of photons have been propagated. The recorded reflection, transmission, and absorption profiles will approach true values. The absorption can be decided in two ways: The usual method that after each propagation step, the photon's weight is reduced by the probability of absorption or the implicit capture technique that provides some absorption information at each photon step, rather than just at times when the photon is completely absorbed [14, 15]. In this article we have used the variable step size Monte Carlo with implicit capture technique to reach desirable accuracy will less photons.At the end of the Monte Carlo simulation, an absorption matrix is obtained which is the raw matrix of total photon weight in each grid element. This matrix with the below formulation then is turned into the absorption photon probability density [14-18]:
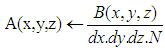 | (1) |
2.2. The Heat Distribution Equation in Tissue
- The laser light absorption results in internal energy increase in the local tissue. The standard Pennes bio-heat equation is still the most commonly used model to describe the thermal behavior of living tissue [9-12, 19-22]:
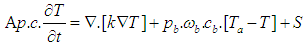 | (2) |
2.3. The Damage Function
- According to the Arrhenius formulation, the degree of tissue damage can be quantified by the damage index Ω [20-27]:
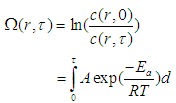 | (3) |
2.4. The Dependences of the Tissue Properties on Tissue Temperature and Damage
- Although no complete temperature and damage dependent thermal properties have been reported, tissue thermal properties can be approximated according to the water content and the dynamic changes of the thermal properties of water in the range of 20–100°C [9-12]:
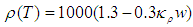 | (4) |
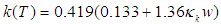 | (5) |
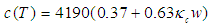 | (6) |
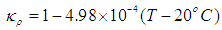 | (7) |
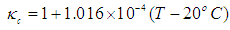 | (8) |
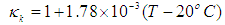 | (9) |
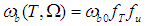 | (10) |
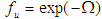 . fT is a dimensionless function that accounts for vessel dilation at slightly elevated temperatures which can be approximated as [9, 10]:
. fT is a dimensionless function that accounts for vessel dilation at slightly elevated temperatures which can be approximated as [9, 10]: | (11) |
3. Model Implementation
- Nd:YAG lasers (1064 nm) or different types of diode lasers (800–980 nm) are usually used as light sources for LITT treatments because of their deeper penetration depths in tissues in the NIR-range [2]. In this study we used 850 nm diode lasers. The values used for this wavelength are listed in Table 1. We have used properties of healthy and cancerous liver for this study [9, 10]. The whole process is done in 3 steps: 1) first the distribution of light in tissue is modeled by Monte Carlo. In each Monte Carlo simulation we have used 50000 photons. 2) The heat generation and transport is calculated using Pennes bio-heat equation. 3) The thermal damage is calculated using Arrhenius equation. Both Pennes bio-heat and Arrhenius equations are modeled using FEM with Comsol Multiphysics 3.5 [28] which utilizes FEM to solve the related governing equations. For irreversible damage, the damage threshold is Ω=1. In LITT, for coagulating the tissue and prevent bleeding laser powers are between 1 to 5W. The contact applicators for this purpose usually have a diameter up to 400µm. In our simulations we used the laser applicator is 10mm long with diameter of 200µm and the laser power of 5W.
|
4. Results
- At first, the dynamic changes of blood perfusion rate is not considered and dynamic changes are considered only for heat conductivity, density and specific heat and the results are compared with constant thermal properties. Then the dynamically changing blood perfusion rate results are considered, when other properties are constant. At the end, the results for all temperature-dependent thermal properties are considered and these three conditions are compared with each other.
4.1. Dynamic Changes of Temperature-Dependent Tissue Properties
- Using equations (4) to (9) in the 3-layer cubic model, the final temperature after 60 seconds with constant and temperature-dependent properties are 89.521°C and 88.848°C respectively. The final damage volumes are also 79.05 [cm3] and 76.001 [cm3] respectively. In the Figures 3 and 4, the temperature increase and damage volume increase during the laser irradiation with constant and changing tissue properties are shown. As can be seen from the results and the Figure, considering the dependence of specific heat, thermal conductivity and tissue density, cause temperature and damage volume to diminish.
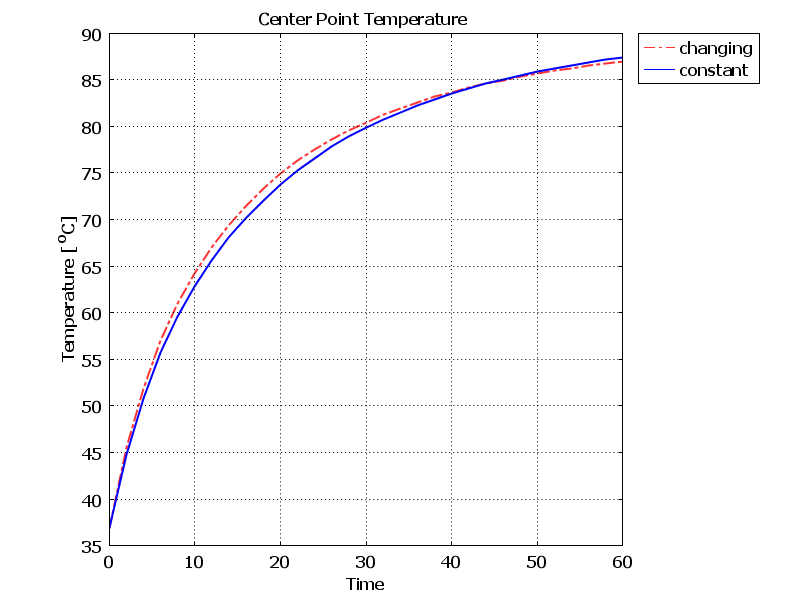 | Figure 3. Temperature increase during laser irradiation at the center of the tissue with constant and changing thermal properties |
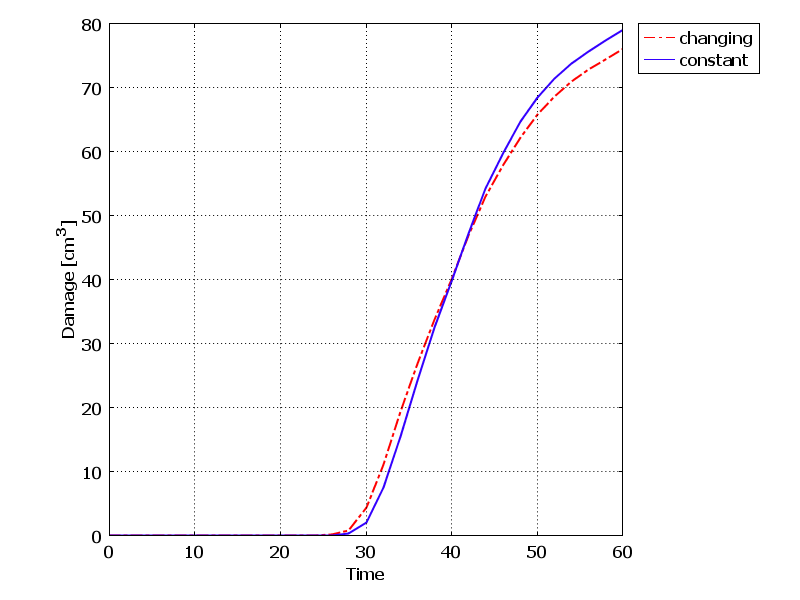 | Figure 4. Damage volume increase during laser irradiation at the center of the tissue with constant and changing thermal properties |
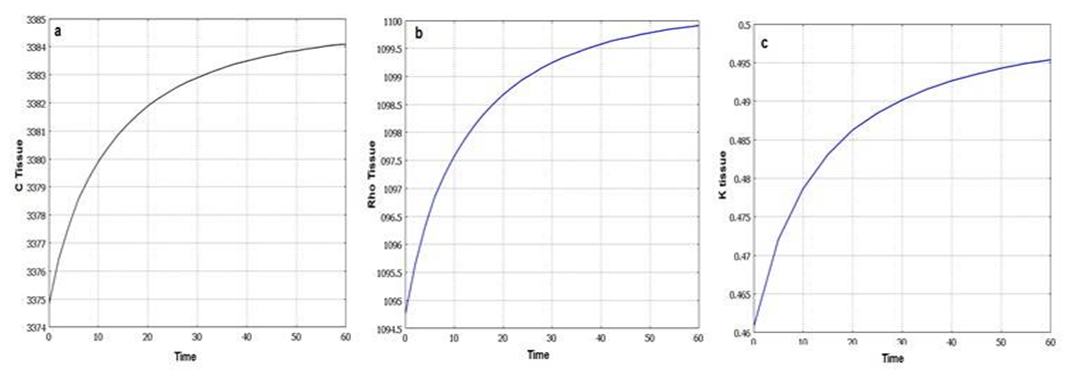 | Figure 5. Dynamic changes of tissue properties during laser irradiation. a) specific heat. b) density. c) heat conductivity |
4.2. Dynamic Changes of Blood Perfusion Rate
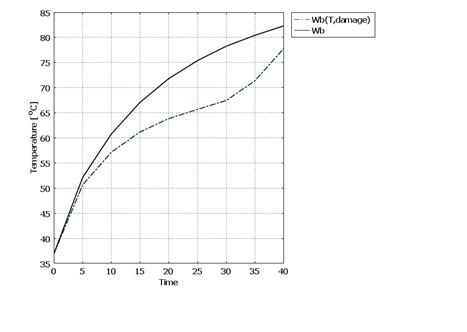
- Blood perfusion rate in tissue has a large impact on heat transfer and damage. Blood perfusion rate with its convective cooling effect of tissue during laser irradiation is an important property in LITT. It is one of the properties of tissue that changes with temperature increase. For modeling blood perfusion rate changes during LITT, we used equations (10) and (11). In this part due to high computational calculations, the simulation time is set to 40 seconds.The results show that final temperature and damage volume with constant properties and with temperature and damage dependent blood perfusion rate are 84.405°C - 26.81[cm3] and 77.566°C - 0.362[cm3] respectively. The temperature increase during laser irradiation in the center of the tissue is shown in figure 6. Due to expansion of blood vessels and increment of blood perfusion rate, cooling properties of blood in the tissue will have a greater impact. Therefore the final temperature is lower comparing with constant tissue properties. After the 30th second, an increase in the slope of the temperature is seen. This is when the blood vessels are destroyed and coagulated due to high temperature in the tissue.
 | Figure 6. Dynamic changes of tissue properties during laser irradiation. a) specific heat. b) density. c) heat conductivity |
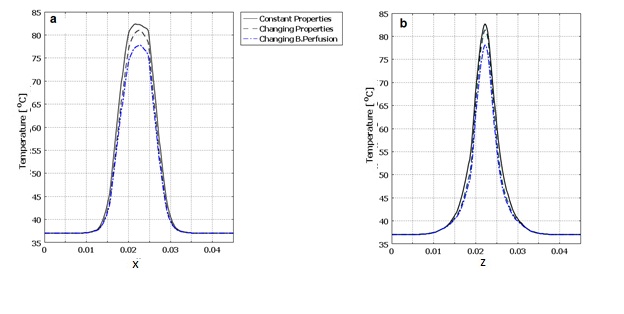
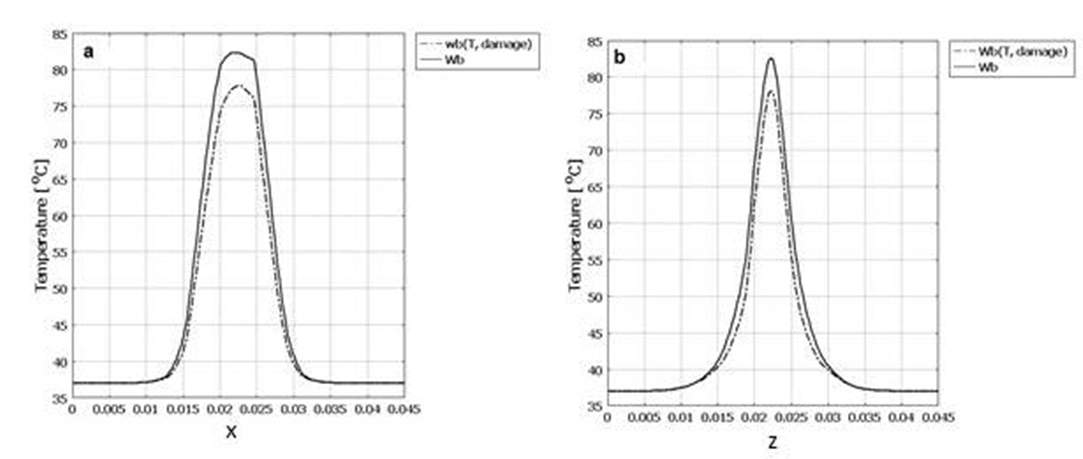 | Figure 7. Temperature expansion of tissue with constant thermal properties and with changing blood perfusion rate. a) In line of applicator position (x axis). b) Tissue depth (z axis) |
4.3. Dynamic Changes of All Temperature-Dependent Tissue Properties Including Blood Perfusion Rate
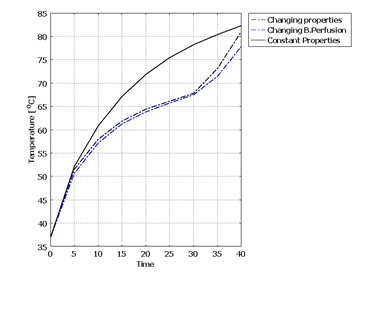
- After considering all thermal and damage dependent properties such as specific heat, heat conductivity, density and blood perfusion rate, the final temperature and damage volume are 83.272°C and 7.96[cm3] respectively.In figure 8 the temperature increase in center point of the tissue after 40 seconds of laser irradiation is shown with 3 conditions of constant properties, dynamic changes of blood perfusion rate only and dynamic changes of all temperature and damage dependent properties. The temperature expansion in line of applicator position (x axis) and tissue depth (z axis) for these 3 conditions are also shown in figure 9.
5. Conclusions and Discussion
- Laser Interstitial Thermotherapy (LITT) is a minimally invasive surgical method to treat cancerous tumours in biological tissues. Using lasers for surgery has many advantages over conventional surgery methods such as increased accuracy, less bleeding and less damage to the tissue. LITT is an effective treatment but has limitations. In order to achieve a safe LITT procedure, a pre-knowledge of the final damage zone is essential in order to prevent injury to adjacent healthy tissues and sensitive structures. One of the parameters that affect the temperature increase in biological tissues is dynamic changes of tissue properties during laser irradiation. In this study, a 3D model was developed to model the effect of dynamic changes of tissue properties and study the final results considering these changes.For that matter, Monte Carlo method with variable step size and implicit capture technique was used to simulate photon transport in tissue. The Pennes bio-heat equation was used for heat generation in tissue. Arrhenius damage function was used to predict the damage volume in tissue. These equations were solved with Finite Element Method simultaneously using Comsol Multiphysics 3.5.Three conditions were considered for studying dynamic changes during LITT: 1) with constant properties, 2) dynamic changes of blood perfusion rate only, 3) dynamic changes of specific heat capacity, heat conductivity, density and blood perfusion rate. The results showed that with constant tissue properties the highest temperature and the largest damage volume occur. The temperature increase and damage volume is higher when considering dynamic changes of all properties rather than blood perfusion rate only. Considering all dynamic changes in tissue properties, this model provides a better understanding of the complex process of laser-tissue interactions during LITT. Hence the physician can have a better planning for LITT treatment. However, these computer simulations should be verified with in vivo experiments in controlled experimental laboratories and with measured optical and thermal properties for any specific patient.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML