-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Biomedical Engineering
p-ISSN: 2163-1050 e-ISSN: 2163-1077
2014; 4(2): 33-40
doi:10.5923/j.ajbe.20140402.02
Optimal Frequency Selection and Analysis Base on Scattering Cross Section for Ultrasound Contrast Second Harmonic Imaging
Ming-Huang Chen , Jenho Tsao
Graduate Institute of Biomedical Electronics and Bioinformations, National Taiwan University, Taipei, Taiwan ROC
Correspondence to: Jenho Tsao , Graduate Institute of Biomedical Electronics and Bioinformations, National Taiwan University, Taipei, Taiwan ROC.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
In ultrasound contrast imaging, the bubble size is essentially time varying, which makes the power of bubble echoes decrease in time. The echo strength of bubble is dominated by resonance, which is bubble size and driving frequency dependent. To optimize SNR and CTR, the imaging frequency must be changed adaptively. An analytical technique, named SCS (scattering cross section) method, for optimal transmission frequency (TxF) selection is proposed. The optimal TxF is selected to be the frequency that the total SCS of a given bubble mixture is maximized. Based on scattering theory of microbubble, the SCS of microbubble can be computed analytically. For quantifying the performance of the SCS method, a power improvement factor of the optimal TxF is defined. The optimal TxF and improvement factor predicted by the SCS method for test cases with different bubble size distributions are presented to show the properties of the SCS method. To show the correctness of the SCS method, improvement factors of the test cases are validated using simulation signals, which are generated by BubbleSim using the optimal TxF predicted by the SCS method. Properties of optimal TxF are exploited using the SCS method. It is found that the optimal TxF is closely related to the resonant frequency of bubbles and the use of optimal TxF is more important for large bubble than for small bubble.
Keywords: Ultrasound contrast imaging, Second harmonic imaging, SCS method, Optimal transmission frequency
Cite this paper: Ming-Huang Chen , Jenho Tsao , Optimal Frequency Selection and Analysis Base on Scattering Cross Section for Ultrasound Contrast Second Harmonic Imaging, American Journal of Biomedical Engineering, Vol. 4 No. 2, 2014, pp. 33-40. doi: 10.5923/j.ajbe.20140402.02.
Article Outline
1. Introduction
- For contrast imaging of blood flow, the quantity of microbubbles changes in the perfusion region of interest and generally the microbubbles have a time varying size distribution. From size distribution measurements, it can be seen that there is a substantial decrease in mean bubble size and in volume fraction of agent with increasing flotation times [1, 2]. Soetanto and Chan measured the size distributions of microbubbles and observed that the distributions were nearly normal distributions and shifted gradually to small sizes over time [3]. Hoff also obtained the similar results, where size distributions were measured by the Coulter Multisizer [4] after varying flotation times. The time varying size property of microbubble will make harmonic images time varying and frequency sensitive. Krishna and Newhouse measured the characteristics of harmonics of different contrast agents and found that the first harmonic decayed more rapidly with time than the second harmonic [5]. Shi and Forsberg showed the amplitudes of the harmonics are time-dependent and quite different for 2-MHz insonification compared to 4-MHz insonification [6].Since bubble echo depends greatly on resonance, which is size and frequency dependent; therefore optimal transmission frequency (TxF) selection is essential to maximize the backscatter power of microbubbles for contrasting imaging to increase SNR. Toilliez et al. [7] and Wyczalkowski [8] et al. proposed optimal techniques to enhance bubble scattering and maximized bubble translation. Reddy and Szeri focused on optimizing the driving pulse to exploit the transient response for pulse-inversion imaging [9]. Menigot et al. suggests Gradient ascent method to find the optimal frequency adapted to microbubble [10]. Kaya et al. assessed the acoustic response of lipid-encapsulated monodisperse microbubbles in response to different excitation frequencies. They investigated means to achieve optimal acoustic response based on the relationship between resonant frequency of microbubbles and center frequency used for transmission [11]. Moon et al. measured microbubble echo signals at various frequencies. They found driving a specific frequency in harmonic mode is capable of maximally resonating micrbubbles with a narrow size distribution could enhanced ultrasound imaging [12]. Optimal TxF can be found using simulating echo responses based on bubble oscillation model, whose results were shown to be in a good agreement with experimentally measured echoes [11]. For this method, each TxF must be considered as input of the simulation model and it costs much time to solve the Raleigh-Plesset equation.In this paper, we propose a theoretical method to search the optimal TxF, which yields maximal power for harmonic chirp imaging [13] and does not need to solve the Raleigh-Plesset equation. This method is based on the scattering cross-section of microbubble given by Church [14] to model the bubble harmonic backscatter power for chirp excitation. In this way, the second harmonic backscatter power can be derived as a function of the second harmonic scattering cross-section, bubble size distribution and square of the transmission signal, which is a function of the TxF. Then the optimal TxF can be taken to be the frequency that can yield maximal power among all possible frequencies. For convenience, this method is named SCS (Scattering Cross-Section) method.In the follows, the theories for required computations are given in section II. Definitions of the SCS method is given fist. For comparison, a method for optimal TxF selection using simulation signals is presented next. In order to verify the SCS method, the improvement factor predicted by the SCS method is compared with that predicted by simulation signals generated by BubbleSim [15] in section III. Some properties of the optimal TxF found by SCS method are presented in section IV. For convenience, the equations of [14] used in this study are digested and put in the appendix.
2. Theories
2.1. Optimal TxF Selection Based on SCS
- Based on Church’s formulation [14], for a microbubble coated with an elastic solid shell, its second-harmonic SCS can found to be a function of driving frequency, f, as
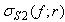 , where r is the radius of microbubble. For convenience, the equations of [14] used in this study are digested and put in the appendix. They include the resonant frequency (A.1) and scattering cross-sections of first and second harmonics (A.2 and A.3).For a mixture of bubbles with size density
, where r is the radius of microbubble. For convenience, the equations of [14] used in this study are digested and put in the appendix. They include the resonant frequency (A.1) and scattering cross-sections of first and second harmonics (A.2 and A.3).For a mixture of bubbles with size density 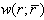 , its second-harmonic SCS can be expressed as sum of the individual second-harmonic SCS's of bubbles with different sizes as:
, its second-harmonic SCS can be expressed as sum of the individual second-harmonic SCS's of bubbles with different sizes as: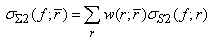 | (1) |
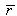 is the mean bubble size, and
is the mean bubble size, and 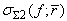 is named TSCS (Total Scattering Cross-Section). Since
is named TSCS (Total Scattering Cross-Section). Since 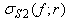 is an analytic solution of the RPNNP bubble equation, its value can be computed easily.In this study, the bubble size density,
is an analytic solution of the RPNNP bubble equation, its value can be computed easily.In this study, the bubble size density, 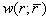 , is assumed to have a Gaussian distribution with
, is assumed to have a Gaussian distribution with 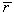 being the mean bubble size and the standard deviation being
being the mean bubble size and the standard deviation being 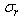 [1, 4]. Since the Gaussian function is an unimodal function, the TSCS is an unimodal function of driving frequency also. This ensure that, for a given bubble size distribution, there is an unique optimal driving frequency
[1, 4]. Since the Gaussian function is an unimodal function, the TSCS is an unimodal function of driving frequency also. This ensure that, for a given bubble size distribution, there is an unique optimal driving frequency 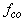 , which can be found as
, which can be found as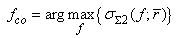 | (2) |
2.2. Optimal TxF Selection Based on BubbleSim Signals
- BubbleSim is a simulation program developed by Hoff for solving the nonlinear bubble equation to get the bubble echo signal
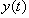 for a given driving signal
for a given driving signal 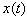 [15]. Unlike the SCS of bubble, the result of BubbleSim can provide much detail information about the bubble echo. This includes the effects of amplitude, frequency, waveform of the driving signal and other bubble characteristic parameters. For the convenience in specifying the harmonics of the bubble signal with different bubble size, the driving and bubble signals will be denoted as
[15]. Unlike the SCS of bubble, the result of BubbleSim can provide much detail information about the bubble echo. This includes the effects of amplitude, frequency, waveform of the driving signal and other bubble characteristic parameters. For the convenience in specifying the harmonics of the bubble signal with different bubble size, the driving and bubble signals will be denoted as 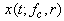 and
and 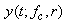 when necessary, where
when necessary, where 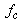 is the center frequency of the driving signal and r is the bubble radius. As in the SCS method, the total power of the second harmonic of bubble echo can be found as
is the center frequency of the driving signal and r is the bubble radius. As in the SCS method, the total power of the second harmonic of bubble echo can be found as 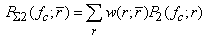 | (3) |
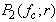 is the second-harmonic power (SHP) of a bubble with radius r. One way to find the SHP is to use the pulse inversion technique [15, 17], which needs to transmit two phase-inverted driving signals to find the second harmonic,
is the second-harmonic power (SHP) of a bubble with radius r. One way to find the SHP is to use the pulse inversion technique [15, 17], which needs to transmit two phase-inverted driving signals to find the second harmonic, 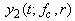 , of
, of 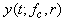 . By Fourier transform, the power spectrum of the second harmonic can be found to be
. By Fourier transform, the power spectrum of the second harmonic can be found to be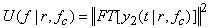 | (4) |
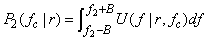 | (5) |
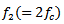 is the twice of TxF and
is the twice of TxF and 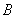 is bandwidth of driving signal. As in the SCS method, the optimal driving frequency,
is bandwidth of driving signal. As in the SCS method, the optimal driving frequency, 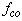 , can be found as
, can be found as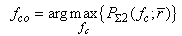 | (6) |
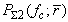 , the bubble equation must be solved for different bubble sizes, which is very time consuming. Even more serious is that the total second harmonic power must be computed for different driving frequencies to find the optimal driving frequency,
, the bubble equation must be solved for different bubble sizes, which is very time consuming. Even more serious is that the total second harmonic power must be computed for different driving frequencies to find the optimal driving frequency, 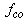 . This will be prohibitive for practical usage.
. This will be prohibitive for practical usage.3. Simulation Studies
3.1. The Use of SCS Method
- For demonstrating the SCS method, the TSCS's of three different mixtures of bubbles are computed for optimal TxF selection. The mean bubble sizes used are 2, 1.5 and 1 μm and the standard deviation of bubble size is set by
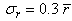 . For each bubble, the SCS of second harmonic are computed using Eq. A.3 with the following settings: Shell thickness = 4 nm, Shell shear modulus = 50 MPa, Shell viscosity = 0.8 Pas, Ambient pressure = 100 KPa, Polytropic exponent = 1, Viscosity of the liquid = 0.001 Pas, Density of the surrounding liquid = 1000 kg/m3 and Density of the shell material = 1100.Three TSCS's are shown in Fig. 1. In each figure, the values of TSCS at two TxF's are given and marked with dashed arrows. One is the optimal TxF and the other is 2.25 MHz for comparison. The TSCS of a TxF is represented as P(TxF); for example, in Fig. 1-a, "P(1.70 MHz) = - 96.4 dB" means that the TSCS at fco=1.70MHz is - 96.4 dB. The TxF, 2.25MHz, is chosen to be a reference case for showing the performance of the optimal TxF and it represents a non-adaptive situation that use a fixed TxF, f0=2.25MHz, despite of the change of bubble size. In dB scale, the difference,
. For each bubble, the SCS of second harmonic are computed using Eq. A.3 with the following settings: Shell thickness = 4 nm, Shell shear modulus = 50 MPa, Shell viscosity = 0.8 Pas, Ambient pressure = 100 KPa, Polytropic exponent = 1, Viscosity of the liquid = 0.001 Pas, Density of the surrounding liquid = 1000 kg/m3 and Density of the shell material = 1100.Three TSCS's are shown in Fig. 1. In each figure, the values of TSCS at two TxF's are given and marked with dashed arrows. One is the optimal TxF and the other is 2.25 MHz for comparison. The TSCS of a TxF is represented as P(TxF); for example, in Fig. 1-a, "P(1.70 MHz) = - 96.4 dB" means that the TSCS at fco=1.70MHz is - 96.4 dB. The TxF, 2.25MHz, is chosen to be a reference case for showing the performance of the optimal TxF and it represents a non-adaptive situation that use a fixed TxF, f0=2.25MHz, despite of the change of bubble size. In dB scale, the difference, 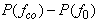 , is the improvement factor (IF) of the optimal TxF relative to the reference TxF,
, is the improvement factor (IF) of the optimal TxF relative to the reference TxF, 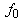 . For the three types of bubble mixture, the improvement factors of using the optimal TxF are 2.5, 0.3 and 7.4 dB.
. For the three types of bubble mixture, the improvement factors of using the optimal TxF are 2.5, 0.3 and 7.4 dB.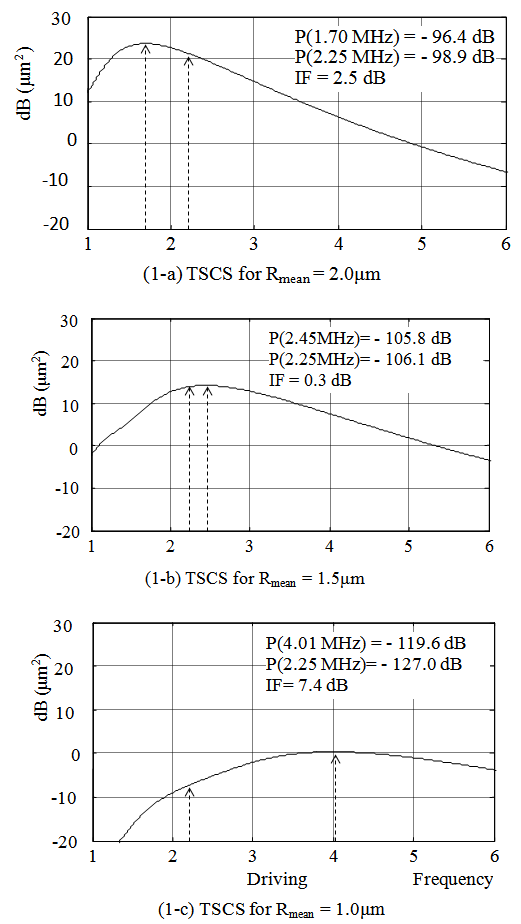 | Figure 1. The TSCS of second harmonic for three types of bubble mixtures |
3.2. Verification of the SCS Method by BubbleSim
- Although the proposed SCS method can find an optimal TxF for a given bubble mixture without solving the bubble equation, its result has nothing to do with the driving signal. In imaging applications, the driving signal is pulsed and bandlimitted, which may have complicated effects on bubble echo due to the nonlinearity of bubble. However this is not a problem for the BubbleSim method, since BubbleSim solves the bubble response for a given driving signal. To verify the usefulness of the optimal TxF predicted by the SCS method, the IF's of the optimal TxF's shown in last section are examined using BubbleSim method.The power of bubble responses to a chirp signal driving at the optimal TxF are found by BubbleSim for comparison with that of the non-adaptive case. The chirp signal is set to have bandwidth = 1 MHz and transmission acoustic pressure = 50 KPa, and is shaped by a Hanning window to have pulse length = 10 μs. In BubbleSim, the bubbles are simulated using the modified Raleigh-Plesset equation with parameters set as in [15]: Shell thickness = 4 nm, Shear modulus = 50 MPa and Shear viscosity = 0.8 Ns/m2. The simulation results are presented using the PSD (Power Spectral Density) of bubble echoes. The PSD of the echoes of a bubble mixture is defined as:
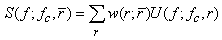 | (7) |
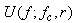 is the power spectrum of the second harmonic of bubble echo as defined in (4). The second harmonic of bubble echo is extracted by the pulse inversion technique and
is the power spectrum of the second harmonic of bubble echo as defined in (4). The second harmonic of bubble echo is extracted by the pulse inversion technique and 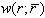 is the bubble density. The PSD's of the same bubble mixtures defined in last section are shown in Fig. 2. In each figure, two PSD's are given, one is for the optimal TxF predicted by the SCS method and the other is for the reference frequency f0= 2.25 MHz. For example, in Fig. 2-a, the black one is the PSD of the second harmonics of the bubbles with mean size = 2 μm driven by the optimal TxF and the blue one is that driven by the reference frequency. Since they are PSD's of simulation signals, they are affected by non-suppressed harmonics. For the black one, its main response is located at 3.4 MHz, which is the second harmonic of TxF = 1.7 MHz, and the other response at 6.8 MHz is the fourth harmonic. Similar results can be found for the reference case. Based on the PSD's, the IF can be found to be 1.3 dB for the 2 μm bubble mixture. For the other two type of bubble mixtures, the improvement factors are 0.2 and 4.3 dB.
is the bubble density. The PSD's of the same bubble mixtures defined in last section are shown in Fig. 2. In each figure, two PSD's are given, one is for the optimal TxF predicted by the SCS method and the other is for the reference frequency f0= 2.25 MHz. For example, in Fig. 2-a, the black one is the PSD of the second harmonics of the bubbles with mean size = 2 μm driven by the optimal TxF and the blue one is that driven by the reference frequency. Since they are PSD's of simulation signals, they are affected by non-suppressed harmonics. For the black one, its main response is located at 3.4 MHz, which is the second harmonic of TxF = 1.7 MHz, and the other response at 6.8 MHz is the fourth harmonic. Similar results can be found for the reference case. Based on the PSD's, the IF can be found to be 1.3 dB for the 2 μm bubble mixture. For the other two type of bubble mixtures, the improvement factors are 0.2 and 4.3 dB.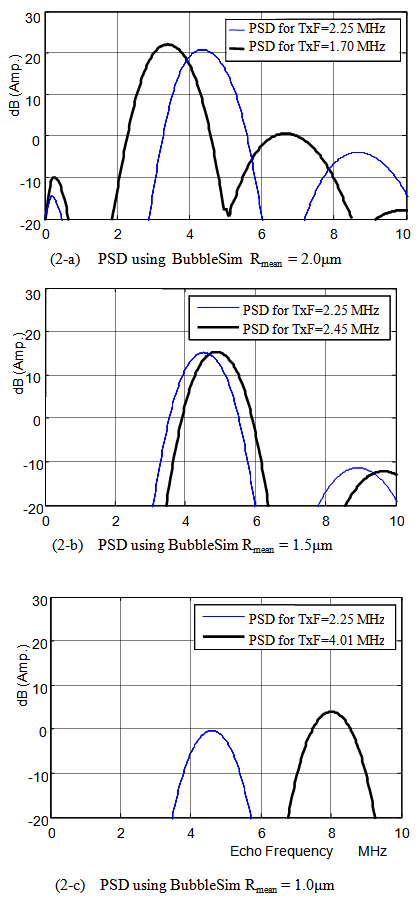 | Figure 2. The PSD of second harmonic for three types of bubble mixtures |
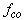 , given in Fig. 1-a, is sharper than those given in Fig. 1-b and 1-c; this means that the TSCS of large bubble is more sensitive to TxF than that of small bubble. 2) A general property of the IF’s is that IF increases monotonically as the distance between the optimal and reference frequencies, i.e.,
, given in Fig. 1-a, is sharper than those given in Fig. 1-b and 1-c; this means that the TSCS of large bubble is more sensitive to TxF than that of small bubble. 2) A general property of the IF’s is that IF increases monotonically as the distance between the optimal and reference frequencies, i.e., 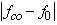 , increases.3) The IF’s predicted by the SCS method is in general larger than those predicted by BubbleSim. However, since these two predicted IF’s are proportional to each other, this is enough to confirm that the SCS method is a proper technique for optimal frequency selection for varying bubble size distribution.
, increases.3) The IF’s predicted by the SCS method is in general larger than those predicted by BubbleSim. However, since these two predicted IF’s are proportional to each other, this is enough to confirm that the SCS method is a proper technique for optimal frequency selection for varying bubble size distribution.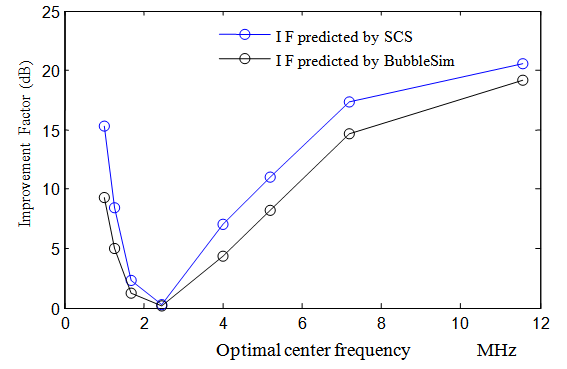 | Figure 3. Improvement factor verification for different mean bubble sizes: 3.0μm ~ 0.4μm |
4. Properties of the Optimal TxF
- The reason that bubble echo intensity can be optimized by TxF is due to the resonant property of bubbles. For a bubble mixture of different sizes, which is known as poly-dispersive bubbles, the bubbles are excited to different degree of resonances; its optimal TxF depends on the mean size as well as the size spread of the mixture. To see the effect of bubble-size spread on the optimal TxF, the optimal TxFs for three types of bubble mixtures are found, using the same parameter setting as in section III.A, and plotted in Fig. 4. The mean bubble size (
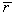 ) is varied from 0.5 to 5μm and the standard deviation of bubble-size is set by
) is varied from 0.5 to 5μm and the standard deviation of bubble-size is set by 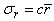 , with c =0,0.1 and 0.3.When
, with c =0,0.1 and 0.3.When 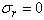 , it is the case of mono-dispersive bubble, i.e., single-sized bubble. The optimal TxF for a bubble with radius
, it is the case of mono-dispersive bubble, i.e., single-sized bubble. The optimal TxF for a bubble with radius 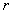 is defined by its SCS at its resonant frequency, i.e.,
is defined by its SCS at its resonant frequency, i.e., 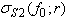 , where
, where 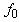 is the resonant frequency. This is the simplest case that the optimal TxF is just the resonant frequency, which is the red curve in Fig.4 computed using Eq. A.1. In general, the resonance frequency of bubble is inversely proportional to bubble size. This property can not be observed easily based on the resonant frequency given by Eq. A.1, since it is not a simple function of bubble size. However, based on other formulations, such as the resonant frequencies given in [4] and [18], the resonant frequency of microbubbles can be approximated as a function of
is the resonant frequency. This is the simplest case that the optimal TxF is just the resonant frequency, which is the red curve in Fig.4 computed using Eq. A.1. In general, the resonance frequency of bubble is inversely proportional to bubble size. This property can not be observed easily based on the resonant frequency given by Eq. A.1, since it is not a simple function of bubble size. However, based on other formulations, such as the resonant frequencies given in [4] and [18], the resonant frequency of microbubbles can be approximated as a function of 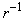 . When bubble particle is described by its bulk modulus
. When bubble particle is described by its bulk modulus 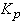 , its resonance frequency can be expressed in a simple form as given by Minnaert
, its resonance frequency can be expressed in a simple form as given by Minnaert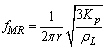 | (8) |
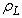 is the density of surrounding liquid.Apparently, the optimal TxFs of poly-dispersive bubble cloud (green and blue) follow the trend of the resonance frequency of single-sized bubbles. This shows that the resonance frequency and SCS of mono-dispersive bubbles is useful for inferring the optimal TxF of poly-dispersive bubble cloud. In general, The resonant frequency increase as mean bubble sizes decrease, so is the optimal TxF. As the property of resonant frequency, it can be said that the optimal TxF is roughly proportional to
is the density of surrounding liquid.Apparently, the optimal TxFs of poly-dispersive bubble cloud (green and blue) follow the trend of the resonance frequency of single-sized bubbles. This shows that the resonance frequency and SCS of mono-dispersive bubbles is useful for inferring the optimal TxF of poly-dispersive bubble cloud. In general, The resonant frequency increase as mean bubble sizes decrease, so is the optimal TxF. As the property of resonant frequency, it can be said that the optimal TxF is roughly proportional to 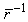 , if the size spread is small. In addition, Fig. 4 shows that the optimal TxF of a poly-dispersive bubble cloud with size distribution parameters
, if the size spread is small. In addition, Fig. 4 shows that the optimal TxF of a poly-dispersive bubble cloud with size distribution parameters 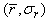 is lower than the resonance frequency of single-sized bubble with
is lower than the resonance frequency of single-sized bubble with 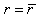 . The larger the
. The larger the 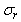 is, the lower the optimal TxF is. This is due to that bubble power can be maximized by reducing TxF to excite larger bubbles
is, the lower the optimal TxF is. This is due to that bubble power can be maximized by reducing TxF to excite larger bubbles 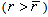 to resonant when
to resonant when 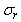 is large.
is large.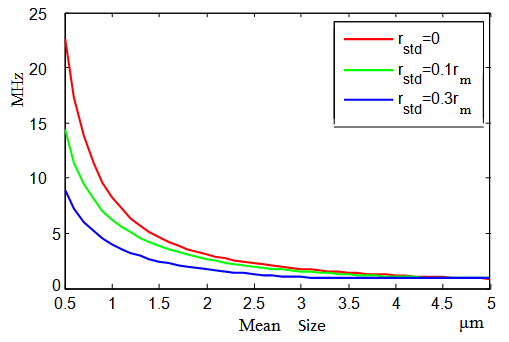 | Figure 4. Optimal TxF for different size spread |
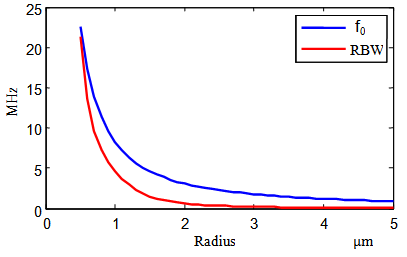 | Figure 5. Resonant frequency and bandwidth (RBW) for bubbles with different size |
5. Conclusions
- For optimizing the SNR in contrast imaging, an analytical technique, named SCS method, for optimal transmission frequency selection is proposed. The correctness of the SCS method is validated using simulation signals generated by BubbleSim. Based on results of the test cases, it is found that the sensitivity of TxF's to bubble size is higher for small bubbles than for large bubbles; however, the sensitivity of IF to TxF is higher for large bubbles than for the small bubbles. Based on the RBW of SCS, it is concluded that the use of optimal TxF is more important for large bubble than for small bubble.Since the SCS method is an analytical technique, it is computationally efficient and can be the basis for developing an adaptive TxF selection technique. However, it needs the knowledge about bubble size distribution. To be an adaptive technique, bubble size distribution must be estimated in time. This calls for a technique to estimate the time-varying bubble size distribution based on bubble echoes.
ACKNOWLEDGEMENTS
- This work is supported by the National Science Council, Taiwan, NSC 102-2221-E-002 -024.
Appendix
- The resonant frequency and scattering cross-section of microbubble digested from [14] are given below. The linear resonant frequency
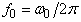 can be predicted by:
can be predicted by: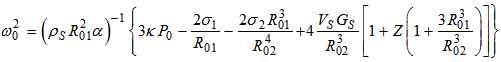 | (A.1) |
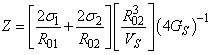 and
and 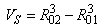 .The scattering cross-section for the first and second harmonics of a bubble coated with an elastic solid and driven by of an incident frequency of
.The scattering cross-section for the first and second harmonics of a bubble coated with an elastic solid and driven by of an incident frequency of 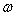 are predicted to be
are predicted to be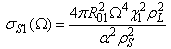 | (A.2) |
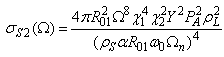 | (A.3) |
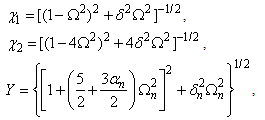
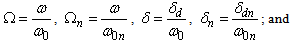
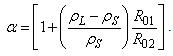
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML