Ojaswita Chaturvedi1, Tiny Masupe2, Shedden Masupe3
1Department of Electrical and Electronics Engineering, University of Botswana, Private Bag UB 0061, Gaborone, Botswana
2School of Medicine, University of Botswana, Private Bag UB 0061, Gaborone, Botswana
3School of Engineering and Technology, Botswana International University of Science and Technology, Private Bag BO 041, Gaborone, Botswana
Correspondence to: Ojaswita Chaturvedi, Department of Electrical and Electronics Engineering, University of Botswana, Private Bag UB 0061, Gaborone, Botswana.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A continuous mathematical model of shigella diarrhea is introduced in this paper. According to the pathogenesis of shigella, the model had been designed as an SIRS system comprising of a non-constant population. The disease-free state and the basic reproduction number (R0) have been computed for this system. In epidemics, there are always two cases: R00> 1 (epidemic existing state). Simulations of the system have been presented for both these cases which show the variations of the population in different situations. Data that has been used for examples and simulations is based on the demographics and disease outbreaks in Botswana.
Keywords:
Epidemic modelling, Mathematical modelling, Shigella
Cite this paper: Ojaswita Chaturvedi, Tiny Masupe, Shedden Masupe, A Continuous Mathematical Model for Shigella Outbreaks, American Journal of Biomedical Engineering, Vol. 4 No. 1, 2014, pp. 10-16. doi: 10.5923/j.ajbe.20140401.02.
1. Introduction
Transmissible diseases constantly present significant world health threats. In general, such diseases are introduced into a closed population by the insertion of an infective individual or by an external vector [1]. Examples of external vectors include water, air, body fluids or biological vectors which carry infectious agents such as protozoa, bacteria or virus. Being essential to life, water is one has a major contribution to the diffusion of infectious diseases. Water related diseases are spread through different uses of water in daily life including bathing, agriculture, washing, food preparation and drinking. Outbreaks primarily result from contaminated water which contains the pathogenic micro-organisms. Direct or indirect ingestion of contaminated water causes the spread of numerous diseases.
1.1. Diarrhoea – Global and National Burden
Diarrhoea is one of the most common diseases that is transferred via contaminated food and water. There are about 1.7 billion cases of diarrhoea annually across the globe [2]. Diarrhoea is known to severely attack children under five and is listed as the second leading cause of mortality in children causing around 700000 child deaths per year [2]. Despite several treatment methods employed, countries worldwide continue to face the high levels of hazards due to diarrhoea. In Bolivia, diarrhoea accounts for 15% of child deaths [19]. England presents a case of diarrhea of one in five people every year [20]. In Namibia, about 30% of child mortality in Namibia is ruled by diarrhea [21].Although it is land-locked, Botswana has predominant water bodies which contribute to the transmission of infectious diseases to a noteworthy extent. According to the statistics obtained from the International Disease Surveillance and Reporting Center of Botswana, there were about 15000 cases of diarrhoea and 200 deaths due to diarrhoea reported in 2012 [3]. This shows that necessary prevention and precaution methods need to be employed so as to avoid health hazards in Botswana.
1.2. Shigellosis
Diarrhoea can be carried by a variation of pathogens including many types of virus, bacteria and protozoa. Shigella, a bacteria genus, causes the infectious disease shigellosis which includes diarrhoea as one of the leading symptoms. Another striking symptom of the disease is dysentery – a special diarrheal case including bloody stools with mucus. Dysentery also remains a principal health hazard in Botswana. Along with the above given statistics, a total number of about 3000 cases of diarrhoea with blood were recorded at the health ministries in the country [3]. Shigellosis can reach high levels of severity in small children and elderly persons due to the low immunity of their bodies. Transmission of the bacteria occurs mainly through the faecal-oral route but indirect transmission by any object that is touched with contaminated hands, e.g. toys, furniture, door knobs and sink surfaces is also common. Food borne transmission also occurs if the food is cooked or handled with contaminated hands. It is possible to be infected by swimming in contaminated water too [4].As the burden of shigella is quite high in the country, a system that incorporates the dynamics and transmission of shigella diarrhoea will prove to be of great advantage. The necessary prevention strategies can be based on the results provided by the system, thus the transmission of the bacteria can be controlled.
1.3. Overview of the Model
Epidemic modelling is a distinctive approach to understanding the disease dynamics. With the increasing threats of infectious diseases throughout the world, models depicting the respective transmission are becoming more important. These models are simply tools that are used to predict the infections mechanisms and future outbreaks of diseases. Although many treatment methods are employed across the globe to combat epidemics such as the diarrhoea, many individuals fail to receive or respond to these methods. Thus, the epidemic models focus more on the prevention mechanisms. Various studies carried out in Botswana prove the importance of diarrhoea prevention in comparison to treatment. The most common treatments given for diarrhea are mainly supportive through the use of Oral Rehydration Therapies (ORT) using Oral Rehydration Salts (ORS).A research work in Botswana showed that only a certain part of the population had access to the ORS. Out of the people who had ORS at their residence, only 74% of them had the knowledge about the preparation and usage. Therefore, while ORS was found out to be widely available, the expected result of successfully defeating the disease was not gained [22].In order to minimize the effects of shigella, a proposed model is presented that designs the dynamics of shigella diarrhoea. The model is essentially of predictive nature that shows the possibility of future outbreaks thus enhancing prevention. On completion, the structure will be incorporated into a system of active maps of the country such that the future prediction will be shown on the maps using graphics highlighting on the expected areas and time periods of infection. A communication platform will also be included in the model which will present an automated alert service to the general public. Any information regarding the disease can communicated easily and fast enough to the public using this facility. The initial stage of building the dynamics of shigella diarrhoea has been elaborated in this paper. A continuous SIRS(Susceptible-Infected-Recovered-Susceptible) model is presented herewith which can be used to derive the discrete model and add on the further enhancements.
2. Background
2.1. Other Models
Many different forms of epidemic models have been introduced in order to overcome the hazardous effects of infectious diseases. With regard to the dynamics of infectious diseases, continuous epidemic models are more common. In 1927, Karmack and McKendrick introduced a compartmental epidemic model consisting of three compartments - the Susceptible-Infected-Recovered (SIR) model [5]. In its simplest form, the SIR model can be depicted as shown in Figure 1.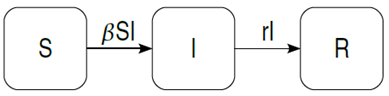 | Figure 1. The Basic SIR model |
Ordinary Differential Equations and some defined parameters are used to define the SIR model as shown below in equations (1) to (3). In the model, β represents the infectivity parameter and r is the rate of recovery. This implies that no randomness is involved in the model [5].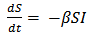 | (1) |
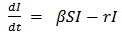 | (2) |
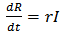 | (3) |
The SIR model has been largely used in Epidemic modeling and is generally found to act as the basis of other models. Following the above traditional model, many other models have been formed in the continuous perspective. The basic model described above has been used by the Biomedical Modeling Centre, LA to model influenza [6]. Simple extensions and modifications have been used here to include factors such as demographics – in/out flow of individuals from the population. The daily incidence of influenza is calculated for different transmission rates using this model. The University of New South Wales, Australia, has also used the basic SIR model and created an agent based model for the Hepatitis C Virus which gives rise to liver diseases. This model uses inputs such as age, sex and immigrant status and delivers outputs such as infections, cure and death rates related to the disease [7]. Data needed for modeling epidemics is usually collected at discrete times [8] and therefore discrete models also confirm to be appropriate in the field. Discrete models are evaluated such that the population size is calculated for the next time interval. This characteristic of discrete models discloses the predictive ability of the model and thus proves to be very advantageous. Discrete models have been widely used to model disease epidemics too. For example, SARS (Severe Acute Respiratory Syndrome) in China has been modeled using discrete modeling by adding three more compartments namely the exposed, quarantined and diagnosed individuals. In this model, the basic reproduction number was used to formulate the asymptotic behavior of the disease and prove the importance of quarantine for such diseases [9]. Diseases such as gonorrhea or malaria are generally modeled using only two compartments, the susceptible and infected classes. Discrete SI and SIS models have been found to be very useful in determining the dynamical behavior of such diseases [10]. An extended study to these models has been done by adding the effects of seasonality in the model. This work uses the fact the seasonal factors have an important relation with the various species in the environment [11].
2.2. Disease Epidemiology and Pathogenesis
Due to the increasing level of infectious diseases throughout the world, there are numerous efforts that are taking place to eliminate the cause and effects of these diseases. Epidemic modeling helps to plan the methods of prevention of infectious diseases, thus reducing the economic requirements and avoiding further infection. In the context of infectious diseases, the severity of water related diseases cannot be overlooked at any cost. Diarrhea is one of the most common water related diseases that continues to endanger the population at large. Diarrhea is caused by bacteria, virus or other parasitic organisms and is predominantly transmitted through contaminated food and water. In order to reduce the speed of the transmission of this disease, it is necessary to recognize the disease characteristics and pathogenesis as this forms the basis of the methods that can be implemented to fight the diffusion of the pathogens.Diarrhea is an infectious disease that is characterized by the passage of three or more liquid stools per day. Apart from the unusual increment in the frequency and liquidity of stool, diarrhea is associated with symptoms such as abdominal pain, fever and most important of all dehydration [12]. Dehydration results in the loss of many necessary salts and chemicals along with water. This situation can become awfully severe, especially in small children and may lead to heavy malnutrition. The symptoms may last from a few hours to a few days, in which case it becomes serious. There are many pathogens that cause diarrhea – as a disease on its own or as a symptom of another disease. As per the national records, the four main pathogens that are attributed to diarrhea in Botswana are the rotavirus, the protozoan cryptosporidium and the bacteria shigella and salmonella. Out of the above list, rotavirus occupies the highest position majorly causing diarrhea in Botswana. In relation to diarrhea, one of the most frequently occurring bacteria, in Botswana, is shigella [13]. As per WHO records, there are approximately 100000 deaths and 90 million cases of shigellosis per year around the world. The basic causes of transmission of the disease are poor hygienic conditions and contaminated edibles, thus the disease is more prominent in countries with poor resources. A very low inoculum of shigella gives rise to efficient transmission. With an infective dose of 10 – 100 organisms [14], shigella has an incubation period of approximately two days. The disease lasts for about a week and the individual remains contagious for a period of four weeks [14]. Shigellosis usually fades away in a few days. If there is persistence, antibiotic treatment can be opted for. Rehydration therapies are used for fluid replacements in the patients. In general, one remains immune to the particular bacteria that had caused the infection. On the other hand, it still remains possible to get infected again by another strain of the shigella bacteria.
3. The Model
3.1. Description
The model considered herewith is a redesigned version based on the SIR model. There are three compartments included in the system, which can be described as follows: 1. Susceptible (S) – this represents the individuals of the whole human population that can catch the disease2. Infected (I) – these are the individuals who have been infected by the bacteria and are capable of passing on this infection to the susceptible population3. Recovered (R) – this class consists of the individuals who have recovered from the disease. These individuals gradually lose their immunity and become susceptible after a certain period of time.A schematic illustration of the model is given below. All the associated parameters are described in Table 1.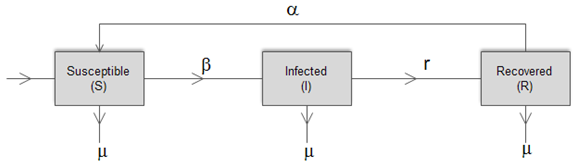 | Figure 2. The extended SIRS model |
| Table 1. Parameter description for the SIRS model |
| | Parameter | Description | | ∏ | Population renewal rate | | β | Infectivity rate | | µ | Natural death rate | | r | Recovery rate | | α | Immunity loss rate |
|
|
The susceptible population, as the name suggests, is non-resistant to the disease and gets in contact with the pathogen through the infected population.The infected class contributes to the pathogen population in the environment and hence transmits the disease. With the help of medication and rehydration therapies or body immunity, the infectious people become recovered. For some time, the body maintains an immunity level but gradually, this level drops and the recovered population again becomes susceptible to the disease.In the above described system, the following assumptions are made:1. The death rate is assumed to be the same for all classes in the model2. All individuals are born as susceptibleUsing the above mentioned parameters and assumptions, the extended compartmental model can be defined using the following equations: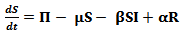 | (4) |
The rate of change of the susceptible population can be described using equation 4 above. A constant recruitment rate ∏ provides new individuals in the class and a constant birth rate µ reduces the susceptible population. A certain proportion of the susceptible get infected at an infectivity rate β depending on the infected population. Recovered individuals gradually join the susceptible class at an immunity loss rate α.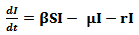 | (5) |
Equation 5 describes the dynamics of the infected class. A portion of the susceptible class become infected and joins in this compartment. The infected population reduces by a constant death rate µ and a recovery rate r. 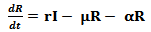 | (6) |
The recovered compartment of the model can be described using the equation 6. As the infected population recovers at the rate r, they get added to the recovered class. People die at a constant death rate µ from the recovered class. A certain part of this compartment gradually loses its immunity at a rate α and moves on again to the susceptible class.
3.2. Parameter Calculations
In order to analyse the above described model, the Virus-free equilibrium has to be calculated. The Disease-free equilibrium (DFE) is the state at which there are no infections in the population. For the population to be deprived of the pathogens, the infected state will be assumed to be zero, i.e. I = 0.Since there are is infectious population, it implies that there will be no recovered population either. Therefore R = 0. At this state, the only non-zero class is the susceptible class. At the DFE, all the classes will be denoted with an asterisk.In order to get the asymptotic state, the non-zero components on the right hand side of equation (4) will be equated to zero. 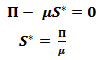 | (7) |
Thus, the DFE can be described using equation 8 as follows: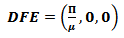 | (8) |
At this point, the basic reproduction number (R0) of the model has to be evaluated. The basic reproduction number can be defined as the number of cases that are generated by a single infection [16]. When modeling diseases, this parameter is used to determine the existence of the epidemic. It is stated that if R0>1, an epidemic exists as there are increasing number of cases. Likewise, if R0<1, then there is no epidemic as the number of cases of infections are decreasing [17]. R0 can be calculated using the next generation matrix, G [17]. The next generation matrix is computed using the infected state(s) and is defined as follows: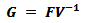 | (9) |
Where F is the Jacobian matrix of the new infections matrix and V is the Jacobian matrix of the other changes in the infected state(s). Calculations here are done at the VFE state. R0 is defined as the highest eigenvalue of the next generation matrix.In the SIRS system portrayed above, there is only one infected state and the basic reproduction number of this model is worked out as: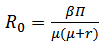 | (10) |
3.3. Numerical Simulations and Discussion
In order to show that the SIRS model depicts a steady system that complies with the stability theorem based on R0, the model was simulated using MATLAB. Table 2 shows the values used for the variables during simulation:| Table 2. Values of parameters used for simulation |
| | Parameter | Value | Source | | ∏ | 10 | [18] | | µ | 0.012 | [18] | | α | 0.25 | Assumed | | r | 0.14 | Assumed |
|
|
The infectivity rate, β, is used to govern the value of the basic reproduction number. For this system, if β < 0.0001824, R0< 1 and if β > 0.0001824, R0> 1. The simulations have been done for various values of β and are shown in the figures below.Figure 3 shows the population variation when β = 0.0001. Since this value is lesser than 0.0001824, the values of R0 is lesser than 1 and there is no epidemic. In a population with no disease, the number of infected persons decreases and the susceptible population increases. Because the infected population is reducing, the recovered population also reduces. This is shown in the graphs in figure 3. It can also be seen from the graphs in figure 3 that lowering the value of β further does not cause any significant changes in the population. Hence, it can deduced that as long as R0< 1, the population will remain disease – free. When β has higher values, R0 becomes more than 1 and an epidemic arises in the population. As expected, figure 4 shows that the susceptible population declines whereas the infected population rises. The recovered population still decreases due to the low recovery rate and high immunity loss rate during epidemics. Figure 4 shows that as the value of R0 is increased, the rate of disease transmission increases. As R0 becomes larger, the respective changes in the susceptible and infected classes become steeper and higher.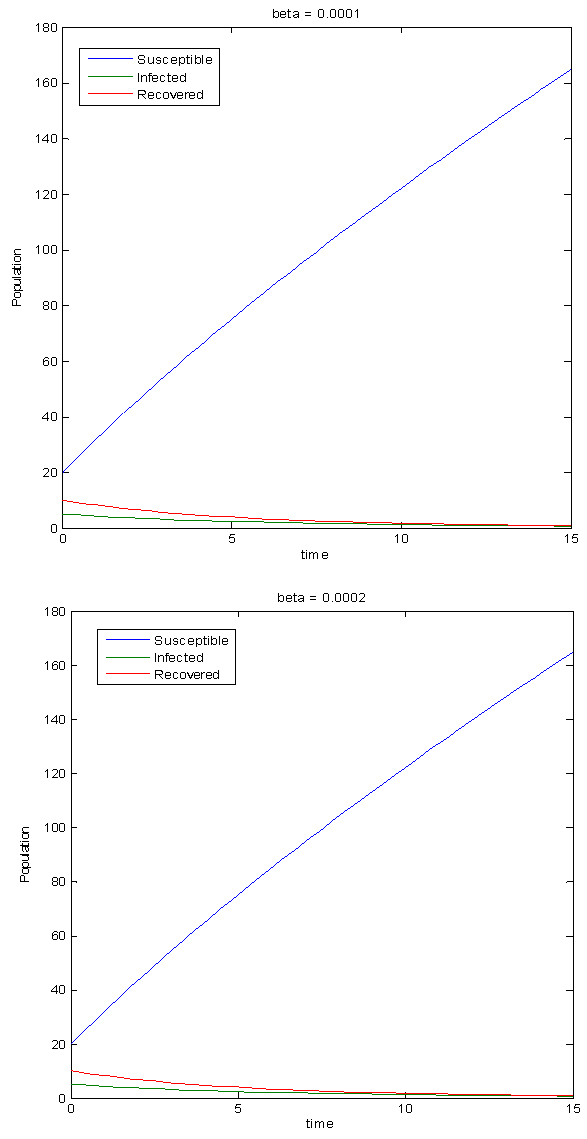 | Figure 3. Simulations for the Disease-free state |
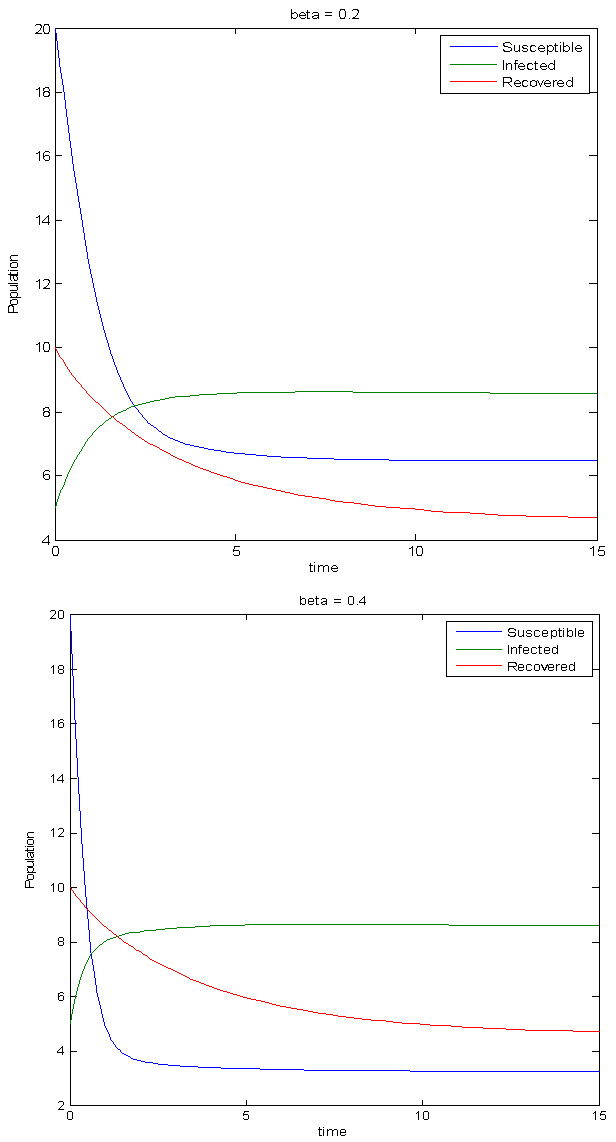 | Figure 4. Simulations for an epidemic situation |
4. Conclusions
This paper presented a continuous model on diarrhea caused by shigella thus provided a better understanding of the dynamics of the disease in a country like Botswana. Analysis of the system was done by evaluating the basic reproduction number and the model was simulated using this evaluated parameter. It was proved that as long as the value of R0 is kept minimal, the disease can be eradicated from the population. The model shows that the higher the value of R0, the more likely an epidemic will spread at higher rates. R0 can be kept low by employing various policies such as increasing knowledge of public in terms of prevention and treatment, increased hygiene conditions at work places and better water treatment facilities.
References
| [1] | Shim E., An Epidemic Model With Immigration of Infectives and Vaccination, University of British Columbia, 2004 |
| [2] | WHO – Diarrheal disease 2013, site:www.who.int/mediacentre, Accessed on 11/4/13 |
| [3] | IDSR data, Botswana Ministry of Health |
| [4] | Todar K., Online Textbook of Bacteriology, Shigella and shigellosis |
| [5] | Debarre F., SIR model of epidemics, Institute of Integrative Biology, ETH Zurich |
| [6] | Coburn B. J., Wanger B. G., Blower S., Modeling influenza epidemics and pandemics, Biomedical Modeling Center, 2009 |
| [7] | Razali K, Thein HH, Bell J, Cooper-Stanbury M, Dolan K, Dore G, et al, Modelling the hepatitis C virus epidemic in Australia, Drug and Alcohol Dependence Journal, 2007 |
| [8] | Brauer F., Feng Z., Chavez C. C., Discrete Epidemic Models, Mathematical Biosciences and Engineering, 2010 |
| [9] | Zhou Y., Ma Z., A discrete epidemic model for SARS transmission in China, Journal of Theoretical Biology, 2003 |
| [10] | Jian-quan Li, Jie L., Mei-zhi L., Some discrete SI and SIS models, Applied Mathematics and Mechanics, 2012 |
| [11] | Franke J. E., Yanuku A., Discrete-time SIS model in a seasonal environment, Journal of applied Mathematics, 2006 |
| [12] | University of California San Francisco medical Center |
| [13] | Rowe J. S. et al, An Epidemiologic Review of Enteropathogens in Gaborone, Botswana, 2010 |
| [14] | Weir E., Shigella: Wash your hands of the whole dirty business, Canadian Medical Association Journal, 2002 |
| [15] | Sedgwick country Health department, Fast facts – Shigella, 2010 |
| [16] | Jones J.H., Notes on R0, Stanford University |
| [17] | Brauer F., Some Simple Epidemic Models, Matehmatical Biosciences and Engineering, 2006 |
| [18] | Botswana demographics, site: www.indexmundi.com, Accessed on 29/5/13 |
| [19] | Burke R. M., Rebolledo P. A., Embrey S. R., Wagner L. D., Cowden C. L., Kelly F. M., The Burden of Pediatric Diarrhea: a Cross sectional study incurred costs and perceptions of cost among Bolivian families, BMC Public Health, 2013 |
| [20] | Casburn-Jines A. C., Farthing M. J. G., GUT International Journal of Gastroentelogy and Hepatology, 2004 |
| [21] | Mobley C.C., Boerma J.T., Titus S., Lohrke B., Shangula K., Black R.E., Variation study of a verbal autopsy method for causes of childhood mortality in Namibia, Journal of Tropical Pediatrics, 1996 |
| [22] | Jammalamadugu S.B., Mosime B., Masupe T., Habte D., Assessment of the household availability of oral rehydration salt in rural Botswana, Pan African Medical Journal, 2013 |

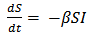
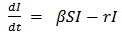
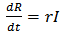

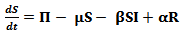
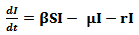
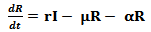
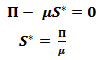
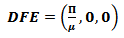
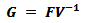
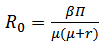


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML