Khalid A. Joudi1, Somer M. Nacy2, Nebras H. Ghaeb2
1Mechanical Eng. Dept., Baghdad University, Baghdad, 10071, Iraq
2Biomedical Eng. Dept., Baghdad University, Baghdad, 10071, Iraq
Correspondence to: Nebras H. Ghaeb, Biomedical Eng. Dept., Baghdad University, Baghdad, 10071, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A comparison between one dimensional mathematical model results, and experimental works for the temperature distribution upon the corneal surface of the human eye when subjected to a laser during eye surgery are presented in this paper. The mathematical formulation is based upon, a 1-D analysis of bioheat transfer equation with the presence of ablation boundary conditions. Whereas the experimental work is based upon temperature measurement using thermocouples embedded in a Polymethyl methacrylate (PMMA) disk with a temperature data logger for the same vision acuity. The agreement between mathematical and experimental data was within ±5%. The mathematical model was modified to study thermal influences on the human eye during a laser surgery and the expected changes in eye power after the refraction surgery.
Keywords:
Lasik, Corneal Surgery, Refractive Surgery, Ablation Heat Transfer, Temperature Measurement of Corneal Surface
Cite this paper: Khalid A. Joudi, Somer M. Nacy, Nebras H. Ghaeb, Temperature Distribution upon Corneal Surface during Laser Eye Surgery, a Comparative Study, American Journal of Biomedical Engineering, Vol. 3 No. 6, 2013, pp. 220-226. doi: 10.5923/j.ajbe.20130306.11.
1. Introduction
In the last few years lasers have been employed widely in different medical applications. From diagnosis to the treatment in different anatomical structures. One interesting application inside the human body is laser surgery of the eye. Laser assisted in situ keratomileusis (LASIK) is one of the important laser techniques used nowadays to reshape the corneal surface for correction of myopia (near sightedness vision), hyperopia (far sightedness vision) and astigmatism. Ophthalmic excimer lasers use ultraviolet radiation at a wavelength of 193 nm is the surgical laser for this process. This wavelength does not heat the tissue but actually breaks inter- and intra- molecular bonds. The concept of ablative surgery is that, by removing small amounts of tissue from the anterior, a significant change of refraction can be attained and is called refractive surgery[1].Recent studies have demonstrated the efficacy, safety, complication and risk factors of refractive surgery[2]. Refractive surgery is based upon manipulating the curvature of the anterior cornea surface to improve the vision quality. The laser ablates the external surface of the cornea (as in the photorefractive keratectomy (PRK), or the internal stroma as in the laser in situ keratomileusis (LASIK) or in the laser epithelial keratomileusis (LASEK). This technique either (1) remodels the anterior curvature, or (2) modifies the compliance of the structure, so that global refractive power of the cornea changes[3]. Further studies are necessary to evaluate their exact significance. In both PRK and LASIK for spherical refractive errors, flattening or steepening of the central corneal curvature due to tissue photo ablation results in decreased or increased refractive power, respectively[4].
2. Mathematical Model
Chua et. al.[5] used the Finite Volume Method (FVM) to predict the 1-D temperature distribution within the human eye when subjected to a laser source. The model predictions showed up to 5% agreement with the experimental data. Narasimhan et. al.[6] used the 2-D FVM to calculate the transient temperature behavior in various regions of the human eye subjected to laser radiation during retinopathy. Berjano and Saiz[6] presented a theoretical model for the study of cornea heating with radio-frequency currents. This technique is used to reshape the cornea to correct refractive disorders. Also the Finite Element Method (FEM) has been used to calculate the temperature distribution in the cornea. Cvetkovic et. Al[7] developed a simple FEM for steady state 2-D temperature distribution. They started the formulation from Pennes bioheat equation and used the Galerkin-Bubnov procedure. Ooi et. al.[8],[9] and[10] used the Boundary element method (BEM) to solve the 2-D and 3-D steady and transient laser effect on the eye. Joudi et. al[11] presented and discussed a 1-D bioheat model for the cornea for LASIK procedure. The final equation for the temperature distribution was: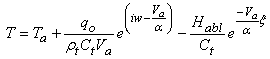 | (1) |
Mathematical results showed that the behavior of temperature is related directly to the laser source frequency when the sampling rate is uniform. This leads to the idea that an increase in temperature of ablated cornea surface may be obtained by increasing the treatment time or increasing the laser source frequency. However, in real and practical laser systems, it is observed that the sampling frequency is not equal for the different LASIK systems. In another words increasing the laser source frequency should be managed by changing the sampling frequency to avoid a rise in temperature and a decrease in the treatment time.
3. Experimental Work
Direct temperature measurement of the cornea surface with contact sensors to the human eye is not easy to accomplish due to the hyper sensitivity of the corneal tissue and the possibility of contamination that may occur. In addition, there would be difficulties in using the laser external source for treatment as the sensors will block the treatment path. In this work, this situation was simulated by using the configuration shown in Figure 1.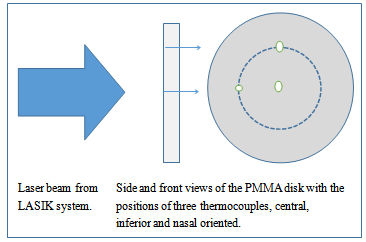 | Figure 1. Configuration used in experimental measurements |
The laser beam in Figure 1, created by the LASIK system “Wavelight ALLEGRETTO WAVE EYE–Q manufactured by Erlangen of Germany” in scanning spot form. This laser beam is prepared according to clinical parameters inserted to the LASIK system from the interface computer. These parameters are calculated from other clinical measurement systems, i.e. Pentacam, Pachymetry, etc. The second part of the configuration is the (PMMA) which is a transparent thermoplastic material developed in 1928 in various laboratories. PMMA has a good degree of compatibility with human tissue and it is used in the manufacture of rigid intraocular lenses in the eye when the original lens has been removed in the treatment of cataracts. The PMMA disk used here was a test ablation sample where the laser shots would be applied onto it and where the thermocouples were inserted inside three drilled holes, with a diameter approximately equal to the laser spot diameter. The thermocouple locations were central, inferior and nasal. The thermocouples temperature accuracy was 0.1℃. This includes the instrumental and calibration error. The measuring tools were:a. Four thermocouples (K–type, 0.75 mm diameter and 321 stainless steel model 406–656 from Tcdirect, UK) with very fine tip. The thermocouples were positioned in three different points of measurement as in Figure 1; central, nasal and inferior. It is important to note that the nasal and inferior positions were at perimeter of a circle 6 mm in diameter inside the treated optical zone OZ = 6.5 mm.b. Dual laser target of 12 inches Infrared Thermometer (IR) (maximum resolution of 0.1℃ Model 42509 from EXTECH instruments a FLIR company, USA) was used to measure the maximum temperature of the ablated disk surface during the laser shots. Also, it was used during the treatment of patient’s eyes during the LASIK surgery. One single maximum temperature was employed for each procedure, which may be used as an indication for the ablation temperature variation with the variation of the vision errors.c. A 4 channel Thermometer / Datalogger (records data on an SD card in Excel format with 0.1℃ resolution Model SDL200 from EXTECH instruments a FLIR company, USA) used for the measurements of the temperature of the ablation disk. Four thermocouples were attached to the datalogger. Three of them which were mentioned earlier, and the fourth was used for the ambient during the laser shots. The logging speed was one value per 0.1 second.An additional eight channel datalogger (records data directly to computer interface Excel format with 0.001oC resolution Model TC-08 from Pico Technology, UK) was used with a speed of thousand values per second. This was much accurate for recording the pulses energy and the ablation effect (see Figure 2).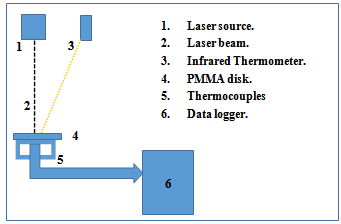 | Figure 2. Experimental measurement setup |
4. Results and Discussion
The temperature distribution on the cornea surface with ablation boundary condition, subjected to 1 mJ with pulse size diameter of 0.5 mm as obtained from eq.1 is shown in figure 3. The frequency of the laser source is 400Hz which is comparable to the frequency of LASIK system used in practical work.It is clear from this figure that the maximum temperature reached around 67℃ which is near the critical temperature for the shrinkage of the collagen fibers of the cornea surface. Exceeding this temperature will lead to the local necrosis, which is the main reason for the creation of irregular astigmatism (high order aberration)[12].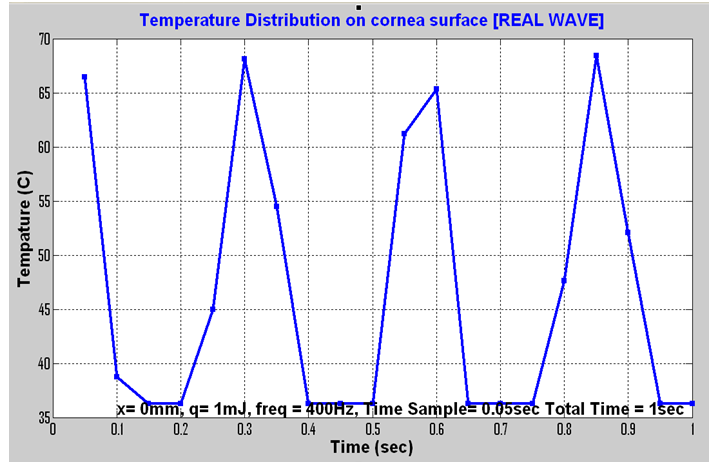 | Figure 3. Temperature distribution according to eq. 1 for 1 mJ[11] |
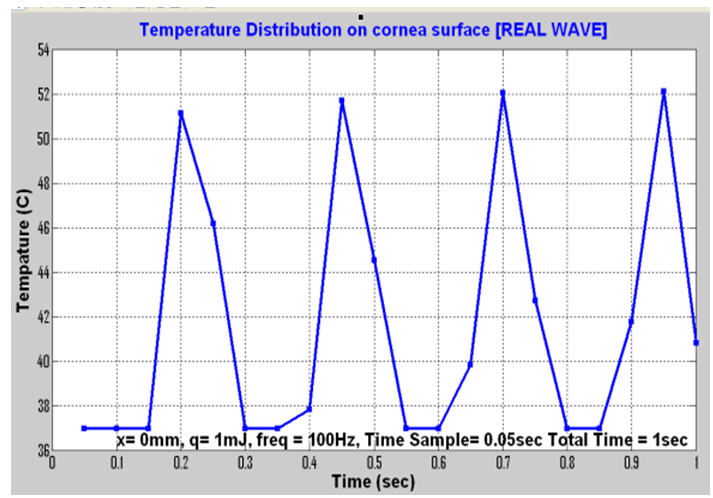 | Figure 4. Temperature distribution according to eq. 1 for 1 mJ[11] |
Due to the high pulse frequencies, there is thought to be a general risk of thermal effects. In LASIK systems, this is prevented by the a smart algorithm which allows only every fifth pulse to overlap a previous one, so that the affected spot has sufficient time to cool in between pulse applications[13]. It is generally accepted that the real shot frequency received per treated position upon the corneal surface is 100 Hz other than 400 Hz. Figure 4 shows the temperature distribution for the 100 Hz as calculated from eq. 1[11], the new maximum temperature value now is about 52℃ which is well below the critical value.Figures 3 and 4 were presented by ref.[11] for central location, time sampling rate about 50 ms and plotted for 1s duration (0.5D treatment). Referring to the technical specifications of the LASIK system shows that the pulse duration for such a system is 12 ns with a special spot criterion based upon Gaussian behavior. This means that a modification of the main laser behavior is required by adding Gaussian function to the actual treatment profile such as[14]: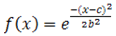 | (2) |
Where x is the independent variable, while b and c are constants for adjusting the central and width of the function. Figure 5 shows this function with different values for b & c.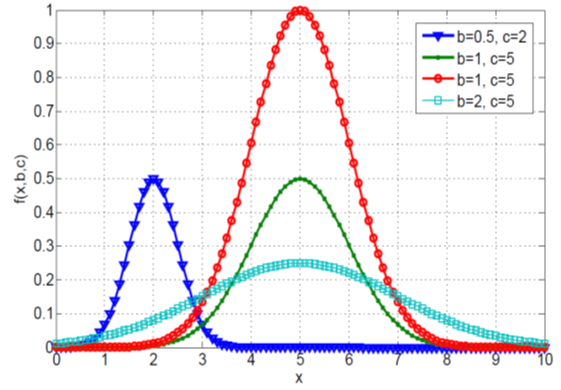 | Figure 5. Behaviuor of Gaussian function, ref[14] |
The LASIK Gaussian beam profile ensures a smooth ablation without grooves or ridges. The tiny 0.68 mm Full Width Half Maximum (FWHM) spot size provides a precise ablation of corneal tissue and very small transition zones[13]. The new treatment temperature profile will become according to eq. 1 at the presence of a Gaussian mask and at a factory setting energy of 1.45 mJ and will be more stable and safer. There is a change in temperature from 33.9℃ to 34.3℃ for a time period of 1s. This is due to the storage effect inside the tissue which is trying to dissipate the conducted part of heat transfer while the ablation releases most of the heat generated at the surface. Reaching this fact theoretically, was supported in this by the experimental measurements of the PMMA disk. Figure 6 shows the behavior of the laser used for correcting the myopic error. This figure shows that during the myopic treatment the central axis of the cornea receives the maximum amount of energy and off course maximum temperature rise (normally the myopic eye is flattened and the hyperopic eye is steepened).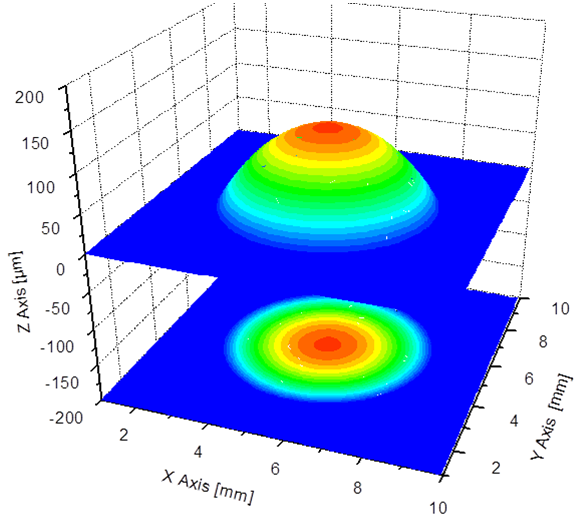 | Figure 6. Myopic treatment laser profile[13] |
Technically, for 6.5 mm optical zone (OZ) the LASIK system spends 2 s/D[13]. Thus 1s duration may be spend for 0.5D. Figure 7 shows the central, inferior and nasal temperatures with both dataloggers; the 4 and 8 Channels while the dotted line at the same figure (figure 7. a) shows the single value measured by IR system during the experimental test (maximum ablation temperature).There are twenty samples (10 sample per second) in this figure. The first 10 samples are the treatment time and recognized by their positive slope which represent the fact that the temperature increases during the treatment time due to the main effect of the tissue thermal storage behavior (conduction effect). While the second 10 samples are the time of relation for the tissue after the laser shots stops, normally this part have negative slope and its length depends strongly upon the tissue storage behavior, practically in the real surgeries a coolant liquid used to decrease this part called BSS (Balanced Salt Solution). Referring back to eq. 1 and modifying it with Gaussian effect eq. 2, the theoretical maximum temperature occurred at the central location is 32.7℃ as it is a myopic correction (flattening the central position) while practically 4ch measures 32.4℃, 8ch 32.698℃ and IR 33.2℃. The temperatures at the nasal and inferior positions at the same instant (measured practically only) about 31.1℃ and 31.2℃ respectively, the differences here due to the asphericity effect inserted through the program of the interface computer of the LASIK system where keratometric readings (Kflat and Ksteep) are not equal. The differences between the 4 ch and 8 ch dataloggers are more significant in the inferior and nasal position than at the central location. Off course the main reason for the difference between the two values (theoretical and practical) are that the first model deals with the human eye tissue while the second deals with a PMMA disk. The shape of the human eye is nearly spherical while the PMMA disk is flat. 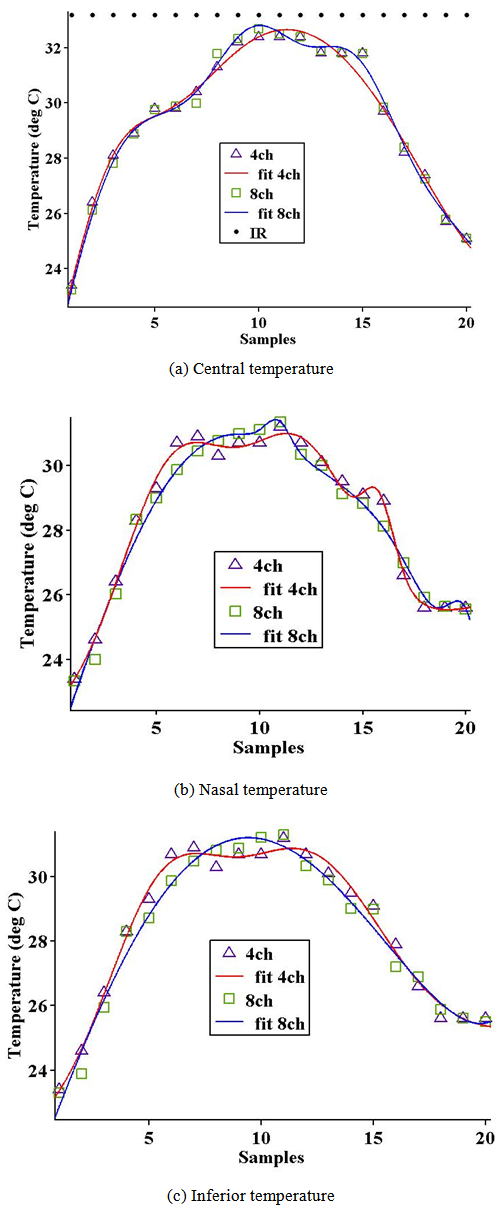 | Figure 7. Temperatures at the central, nasal and inferior locations in the PMMA disk for myopic 0.5D |
Also, there is fluctuation in energy of treatment during the practical measurement the environmental conditions and temperature measurement accuracy inherent the measuring technique[15]. The differences between the measurements of the central, (inferior and nasal) locations and the two dataloggers themselves are more significant in case of high myopic correction (see Figure 8). The expected treatment time will be 12 s. 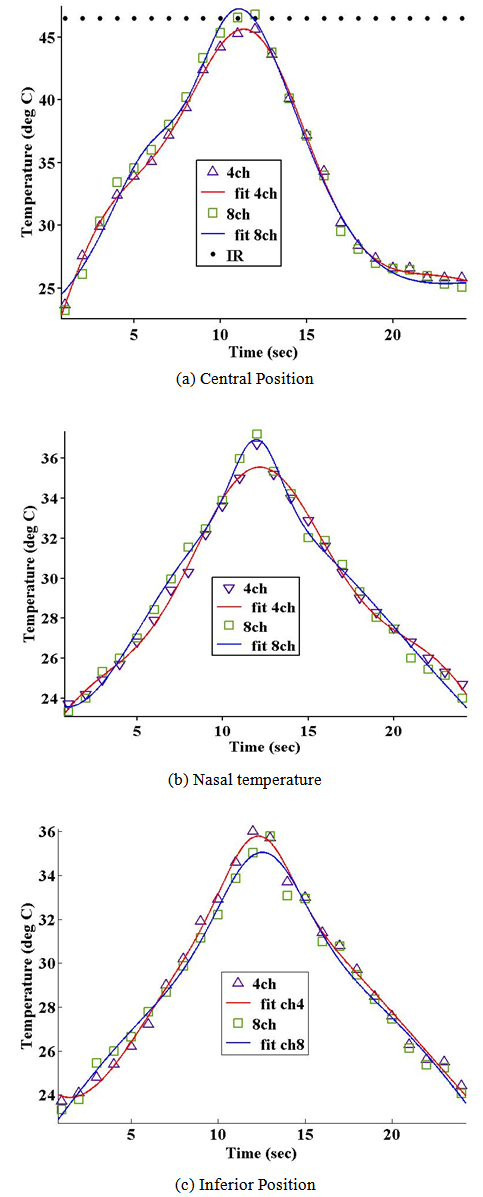 | Figure 8. Temperature measurements of the two dataloggers (4 and 8 channels) for myopic 6.0D |
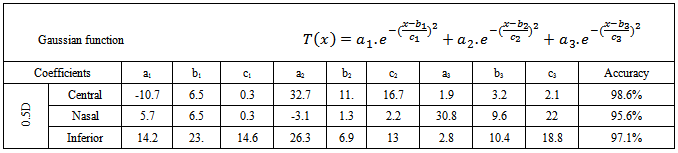
Table 1. Gaussian Coefficients for profiles of central, nasal and temporal of 0.5D myopic correction for 8ch
 |
| |
|
The central temperature calculated from the modified eq.1 and 2 here is equal to 45.5℃ while the maximum temperature recorded through the data loggers and IR are 45.6℃, 46.789℃ and 46.5℃ respectively. Still we have acceptable range of differences between the theoretical and experimental works. Return back to the behavior of the central location temperature the differences between the two loggers reached to 1.2℃ after 12 s of treatment, while nasal position recorded differences reach to 0.98℃.Applying the curve fitting technique for the measured values considering the modified Gaussian temperature profile we reached to fact that the practical temperature profile is third order Gaussian function while the theoretical once is second ordered Gaussian. Table 1 shows the Gaussian coefficient values for the profiles at the central, nasal and temporal positions for 0.5D.For human cornea tissue, the ablation threshold of about 48 mJ/cm2 and the absorption coefficient is about 3.5 µm-1, while for PMMA, the ablation threshold takes value (72 mJ/cm2 and 4.5 µm-1)[17]. By calculating the volume of single spot for the cornea, and divided it by the volume of a single impact on PMMA, a so called Cornea to PMMA ration (CTPR) appears. This ratio can be considered about 1.05 at the central location and about 1.15 at an optical zone of 1.15. The differences between the two values mainly due to the shape differences (flat PMMA and asphere cornea), and this fact leads to good agreement between mathematical and measured values at the central other than the peripheral. Finally comparing the accuracy of each function with the mathematical calculated values, return back with good agreement between them reached to ±5% for each location. It is very good to say that we can adopt the mathematical modified function to calculate the maximum temperature upon corneal surface during the LASIK treatment and this is approved with practical measurements.
5. Conclusions
The modified mathematical formulation of Juodi et al.[13] with the Gaussian profile of eq.2 and using the LASIK configuration parameters for the laser beam gives a more accurate prediction of the temperature above the central location of the cornea during laser eye surgery. 1. The experimental measurements of the temperature in the center of the PMMA disk and agree well with the theoretical model values. 2. Datalogger of a high sampling rate are preferred for better accuracy of experimental temperature measurements. Calculating the temperature distribution in the corneal surface is very important for the indication of safety margins and is related directly to the post healing process after treatment.
References
| [1] | B. F. BOYD, M.D., F.A.C.S., "Lasik and Beyond Lasik Wavefront Analysis and Customized Ablations", Copyright, English Edition, 2002 by HIGHLIGHTS OF OPHTHALMOLOGY. |
| [2] | M. A. Widlicka, W. Srodka, P. K. Berkowska, "The biomechanical modelling of the refractive surgery", Int’l J. for Light and Electron Optics; Optik, Vol. 120, (2009), pp 923–933. |
| [3] | A. Pandolfi, G. Fotia, and F. Manganiello, "Finite element simulations of laser refractive corneal surgery", Engg. with Computers (2009) vol. 25, Issue No. 1, pp15–24. |
| [4] | S. H. Mahmoud, N. E. H. Ismail, and A. I. Salem, "A Novel Simulation and Analysis Scheme for Human Eye Ablation", IEEE, Int’l Conf. on Computer Engg. & amp. Systems, 2007, pp 262-265. |
| [5] | K.J. Chua, J.C. Ho, S.K. Chou and M.R. Islam, "On the study of the temperature distribution within a human eye subjected to a laser source", Int’l Comm. in Heat and Mass Transfer Vol. 32 (2005), pp 1057–1065. |
| [6] | A. Narasimhan, K. Jha and L. Gopal, "Transient simulations of heat transfer in human eye undergoing laser surgery", Int’l J. of Heat and Mass Transfer vol. 53 (2010), pp 482–490. |
| [7] | M. Cvetkovic, D. Cavka and D. Poljak, "A Simple Finite Element Model of Heat Transfer in the Human Eye", IEEE, Int’l Conf. on Software in Telecomm. and Computer Networks 2006, pp: 27-31. |
| [8] | E. H. Ooi, W.T. Ang and E.Y.K. Ng, "Bioheat transfer in the human eye: A boundary element approach", Engg. Analysis with Boundary Elements Vol. 31 (2007), pp 494–500. |
| [9] | E. H. Ooi, W.T. Ang and E.Y.K. Ng, "A boundary element model of the human eye undergoing laser Thermo keratoplasty", Computers in Biology and Medicine Vol. 38 (2008), pp 727–737. |
| [10] | E. H. Ooi, W.T. Ang and E.Y.K. Ng, "A boundary element model for investigating the effects of eye tumor on the temperature distribution inside the human eye", Computers in Biology and Medicine Vol. 39 (2009), pp 667–677. |
| [11] | K. A. Joudi, S. M. Nacy and N. H. Ghaeb, “One Dimensional solution for temperature distribution upon corneal surface during laser surgery”, 6th Cairo Int’l Biomedical Engineering Conf., 2012. |
| [12] | American Academy of Ophthalmology, “Refractive surgery – section 13”, Lifelong Education for the Ophthalmologist (LEO), 2011 – 2012. |
| [13] | Alcon surgical, “Wavelight Allegretto Wave eye-Q”, Tech. data and ref. website based information,http://www.alconsurgical.com/. |
| [14] | Hongwei Guo, "A simple algorithm for fitting a Gaussian function," IEEE Sign. Proc. Mag. 28(9): 134-137 (2011). |
| [15] | A. J. Welch and M. J.C. van Gemert,”Optical-Thermal Response of Laser-Irradiated Tissue”, chapter (11) Temperature Measurements, Springer Science Business Media B.V. 2nd edition, 2011. |
| [16] | D.T Azar and D.D. Koch, ”LASIK, Fundamental, Surgical Techniques and complications”, Marcel Dekker, Inc. 2002. |
| [17] | S. A. Mosquera, “Optimization of the ablation profiles in customized treatments for laser corneal refractive surgery”, a Ph. D thesis submitted for University of Valladolid, Spain, (2010), pp 63 – 65. |

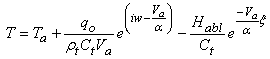




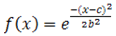




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML