-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Biomedical Engineering
p-ISSN: 2163-1050 e-ISSN: 2163-1077
2012; 2(3): 98-104
doi: 10.5923/j.ajbe.20120203.02
MRI Monomodal Feature-Based Registration Based on the Efficiency of Multiresolution Representation and Mutual Information
Nemir Al-Azzawi1, Wan Ahmed K. Wan Abdullah2
1School of Electrical and Electronic Engineering, USM, 14300, Malaysia, (Universiti Sains Malaysia)
2Department of Radiology, School of Medical Sciences, USM, Malaysia, (Universiti Sains Malaysia)
Correspondence to: Nemir Al-Azzawi, School of Electrical and Electronic Engineering, USM, 14300, Malaysia, (Universiti Sains Malaysia).
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Image registration methods based on mutual information criteria have been widely used in monomodal medical image registration and have shown promising results. Feature-based registration is an efficient technique for clinical use, because it can significantly reduce computational costs. In general, the majority of registration methods consist of the following four steps: feature extraction, feature matching, transformation of the models and, finally, resampling the image. It was noted that the accuracy of the registration process depends on matching a feature and control points (CP) detection. Therefore in this paper has been to rely on this feature for magnetic resonance image (MRI) monomodal registration. We have proposed to extract the salient edges and extracted a CP of medical images by using efficiency of multiresolution representation of data nonsubsampled contourlet transform (NSCT). The MR images were first decomposed using the NSCT, and then Edge and CP were extracted from bandpass directional subband of NSCT coefficients and some proposed rules. After edge and CP extraction, mutual information (MI) was adopted for the registration of feature points and translation parameters are calculated by using particle swarm optimization (PSO). We implement experiments to evaluate the performance of the NTSC and MI similarity measures for 2-D monomodal registration. The experimental results showed that the proposed method produces totally accurate performance for MRI monomodal registration.
Keywords: Monomodal Registration, Feature-Based Registration, Mutual Information, Nonsubsampled Contourlet Transform (NSCT), Particle Swarm Optimization (PSO)
Article Outline
1. Introduction
- Monomodal image registration in medical images is one helpful technique. It is a problem of major interest in almost all applications in medical image processing and clinical applications. For example, surgical planning, image guided surgery, surgery simulation, radiotherapy, disease monitoring, longitudinal studies, pathology survey, control, medical treatment, post-operative control and many other applications in diagnosis and therapy. It is based essentially on the similarity criterion measurement because it defines the objective criterion used to estimate registration quality between the homologous structures of images. Brain’s imaging is particularly essential as well for the knowledge of the functional and/or pathological processes, as for the improvement of adapted strategies of treatment. The technique of monomodal feature-based registration of serial magnetic resonance scans its application to neuropsychiatric disorders, such as schizophrenia, depression and Huntington's disease[1]. Thus, these last years, many researchers predictable the need to develop treatment tools in order to assist the expert in his diagnosis choice[1-3]. Generally, it is a clinical aided system dedicated to make the assessment. For example, in neurosurgery it is currently helpful to identify tumors with magnetic resonance images (MRI).Previous work on medical image registration can be characterized based on the used image information into intensity-based methods and feature-based[4]. The first class utilizes an image intensity to estimate the parameters of a transformation between two images using an approach involving all pixels of the image. In contrast, the second class does not work directly with image intensity values and rely on establishing feature correspondence between the two images. The feature-based matching algorithm may be performed by iterative closest point (ICP) algorithms[5] or by optimizing deformable models[6]. These methods, firstly, uses feature matching techniques to determine corresponding feature pairs from the two images, and then compute the geometric transformation relating them.The accuracy of a registration algorithm is consequently, affected by the segmentation and feature extraction algorithms[4]. Researching and exploring a more accurate and faster registration algorithm is a very important domain. The main advantage of feature-based method, where a matching algorithm is sought between corresponding objects within the images, is approximately invariance for the intensity characteristics of the pixels. This method is sensitive to the error of feature extraction and matching[7]. Wavelet bases are commonly used to generate features for image registration to handle the accurate feature extraction[8-9]. Nonsubsampled contourlet transform (NSCT) can be able to capture significant image features across spatial and directional resolutions[10-11]. It is ordinary to ask whether mutual information can play a comparable role in feature-based matching as well. Rangarajan[12] demonstrates that mutual information can be utilized to parameterize and solve the correspondence problem in feature-based registration.
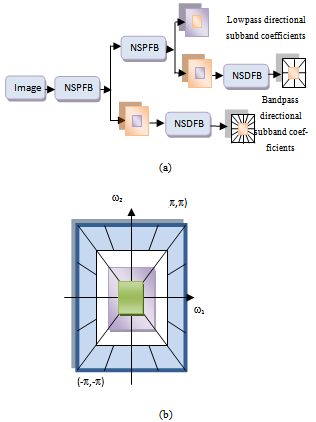 | Figure 1. (a) Nonsubsampled contourlet transform NSCT. (b) Resulting frequency division |
2. Nonsubsampled Contourlet Transform
- Do and Vetterli developed a true 2-D image representation method, namely, the contourlet transform[13], which is achieved by combining the Laplacian pyramid (LP)[14] and the directional filter bank (DFB)[15]. Compared with the traditional wavelet, contourlet transform can represent edges and other singularities along curves much more efficiently due to ability to multi-direction and anisotropy. However, the contourlet transform lacks the shift-invariance, which is desirable in many image applications. In 2006, Cunha et al. [10] proposed the NSCT which is a fully shift-invariant version of the contourlet, and multidirectional expansion that has a fast implementation. The NSCT eliminates the downsamplers and the upsamplers during the decomposition and the reconstruction of the image; instead, it is built ahead the nonsubsampled pyramids filter banks (NSPFBs) and the nonsubsampled directional filter banks (NSDFBs). The NSPFB, employed by the NSCT, is a two-channel nonsubsampled filter bank (NFB). The NSCT is obtained by carefully combining the NSPFB and the NSDFB [10], as shown in Figure 1.
3. The Proposed Registration Algorithm
- Given two images, IR (defined as a reference image) and IU (defined as a unaligned image) to match the reference image, the goal of image registration is to fix the unaligned image into the coordinate system of the reference image and to make corresponding coordinate points in the two images fit the same geographical location. In this section, we present the registration algorithm. There are three main steps carried out for registration.
3.1. Edge Detection using NSCT Transform
- In order to extract two sets of feature points, CP1i (i=1,2,…N1)and CP2i (i=1,2,…N2) from the reference and the unaligned images respectively, a NSCT-based feature points extraction method is employed. The method can be summarized by the following steps:Step 1: Compute the NSCT coefficients of both reference and unaligned images for J-levels.Step 2: Using only bandpass directional subband coefficients, compute the maximum magnitude of all directional subbands at a specific level J, where it’s contained all high frequency that can be extracted edges. This call “NSCT-maxima image. At this step we get NSCT- maxima reference image and NSCT- maxima unaligned image.Step 3: Control points CP is found by applying a threshold procedure
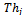 to both NSCT-maxima reference and unaligned image respectively. Using[12,16] following rule:
to both NSCT-maxima reference and unaligned image respectively. Using[12,16] following rule: | (1) |
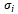 and
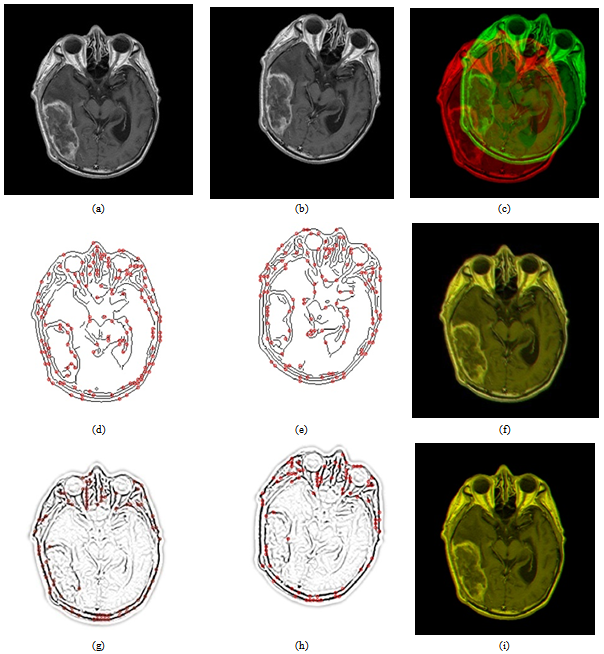
and 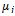 are the standard deviation and mean of the NSCT maxima image. A low standard deviation indicates to be very close to the same value (the mean), while high standard deviation indicates that the data are spread out over a large range of values.Step 4: The locations of the obtained threshold NSCT -maxima CP1i (i=1,2,…N1) and CP2i (i=1,2,…N2) are taken as the extracted feature points. where CP1i , CP2i are the coordinates and N1,N2 are the number of feature points. An example of the feature points detected is shown in Figure 4.
are the standard deviation and mean of the NSCT maxima image. A low standard deviation indicates to be very close to the same value (the mean), while high standard deviation indicates that the data are spread out over a large range of values.Step 4: The locations of the obtained threshold NSCT -maxima CP1i (i=1,2,…N1) and CP2i (i=1,2,…N2) are taken as the extracted feature points. where CP1i , CP2i are the coordinates and N1,N2 are the number of feature points. An example of the feature points detected is shown in Figure 4.3.2. Optimizing the MI Based on Particle Swarm Optimization
- After the feature points of two images have been extracted, mutual information (MI) is employed as a similarity measure to be optimized. Since MI made its entrance into the field of medical image registration, it has been adopted by a large number of researchers[17-19]. Let
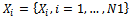 be points of NSCT-maxima reference image and
be points of NSCT-maxima reference image and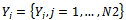 be points of NSCT-maxima unaligned image. The mutual information between the point-sets is a function of the joint probability as follows:
be points of NSCT-maxima unaligned image. The mutual information between the point-sets is a function of the joint probability as follows: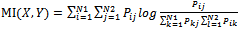 | (2) |
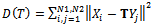 | (3) |
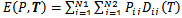 | (4) |
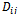 should be small for homologies and large for non-homologies. The maximum entropy method attempts to maximize the number of correspondence possibilities while being constrained by the expected point matching. The solution for the joint probability
should be small for homologies and large for non-homologies. The maximum entropy method attempts to maximize the number of correspondence possibilities while being constrained by the expected point matching. The solution for the joint probability 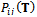 is:
is: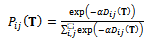 | (5) |
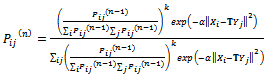 | (6) |
 | Figure 2. The overall proposed algorithm is described in the pseudo-code |
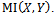 . The Basic PSO algorithm consists of the velocity:
. The Basic PSO algorithm consists of the velocity: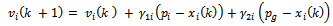 | (7) |
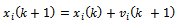 where, i is particle index, k is discrete time index, vi is velocity of ith particle, xi is position of ith particle, pi is best position found by ith particle (personal best), pa is best position found by swarm (global best, best of personal bests) and
where, i is particle index, k is discrete time index, vi is velocity of ith particle, xi is position of ith particle, pi is best position found by ith particle (personal best), pa is best position found by swarm (global best, best of personal bests) and 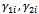 are random numbers on the interval [0,1] applied to ith particle.The PSO can be easily extended[8,21]. By assuming a set of m particles in D-dimensional searching space, in which the first particle stands for a D-dimensional vector
are random numbers on the interval [0,1] applied to ith particle.The PSO can be easily extended[8,21]. By assuming a set of m particles in D-dimensional searching space, in which the first particle stands for a D-dimensional vector 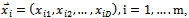 it is the position of
it is the position of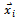 . In other terms, every position is a prospective resolution. The corresponding value is obtained when
. In other terms, every position is a prospective resolution. The corresponding value is obtained when 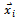 is set to the target function. Set the present optimal position of the first particle is
is set to the target function. Set the present optimal position of the first particle is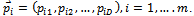 The present optimal position of the swarm is
The present optimal position of the swarm is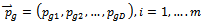 . Operating the particles with the formulas:
. Operating the particles with the formulas: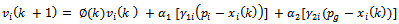 | (8) |
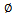 is inertia function,
is inertia function, 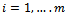 and a1,2 is nonnegative acceleration constants.
and a1,2 is nonnegative acceleration constants. 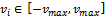 where,
where,  is a constant value and it is set by the user. The ending condition of the iteration is essentially decided by the largest iteration or the threshold of the optimal position of the particles. By taking MI, this is depending on the parameters as the value of the target function.
is a constant value and it is set by the user. The ending condition of the iteration is essentially decided by the largest iteration or the threshold of the optimal position of the particles. By taking MI, this is depending on the parameters as the value of the target function.3.3. Transformation Parameters Estimation
- Image geometrical deformation has many different ways of description[7]. The linear transformations which are a combination of rotation
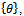 , scaling
, scaling 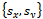 and translation
and translation 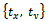 are the most common one. Linear transformations are global in nature, thus not being able to model local deformations. Generally, shearing components are not needed for registration, so that in this case the linear transformation is an affine one. Each parameter was chosen independently and uniformly from the possible ranges. Given the two sets of corresponding feature point coordinates optimum CP, the estimation of the transformation parameters, required to transform the unaligned image into its original size, direction, and position. The mutual information alignment algorithm was executed almost exactly as described in the previous section. The proposed feature-based image registration algorithm is illustrated in Figure 3.
are the most common one. Linear transformations are global in nature, thus not being able to model local deformations. Generally, shearing components are not needed for registration, so that in this case the linear transformation is an affine one. Each parameter was chosen independently and uniformly from the possible ranges. Given the two sets of corresponding feature point coordinates optimum CP, the estimation of the transformation parameters, required to transform the unaligned image into its original size, direction, and position. The mutual information alignment algorithm was executed almost exactly as described in the previous section. The proposed feature-based image registration algorithm is illustrated in Figure 3.4. Numerical Experiments
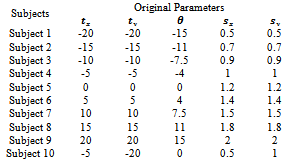
- To validate the registration systems, numerous experiments were conducted. Ninety subjects of human brain images are selected from Hospital Universiti Sains Malaysia (HUSM). Table 1 is shows only ten subjects. MRI image is used as reference and subject images as unaligned. The images have the resolution (x= 256, y=256 and z=20-24) with 256-level grayscale and voxel size (x=1.25, y=1.25 and z=5 mm). Subject images were synthetically generated by adjusting the transformation parameters relative to the reference image
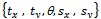 are translating, rotating and scaling in x, y directions. Table 1, is indicating the spatial relations between the reference image and subject images. Registration systems were implemented in MATLAB software package and tested on an Intel core 2 Duo, 2.53 GHz. The experiment was implemented according to the following settings: The NSCT decomposition of images, performed using the NSCT Matlab toolbox, was carried out with a level=[0,1,3] directional filter bank decomposition levels at each pyramidal level (from coarse to fine scale) and c=1.8. An experimental result was compared with the method[12] based on canny edge method. A registration results for canny edge extraction and NSCT edge extraction is shown in Figure 4.Registration settings: For the both canny edge extraction and NSCT edge extraction. The initial transformation parameters
are translating, rotating and scaling in x, y directions. Table 1, is indicating the spatial relations between the reference image and subject images. Registration systems were implemented in MATLAB software package and tested on an Intel core 2 Duo, 2.53 GHz. The experiment was implemented according to the following settings: The NSCT decomposition of images, performed using the NSCT Matlab toolbox, was carried out with a level=[0,1,3] directional filter bank decomposition levels at each pyramidal level (from coarse to fine scale) and c=1.8. An experimental result was compared with the method[12] based on canny edge method. A registration results for canny edge extraction and NSCT edge extraction is shown in Figure 4.Registration settings: For the both canny edge extraction and NSCT edge extraction. The initial transformation parameters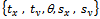 were bounded in the following way
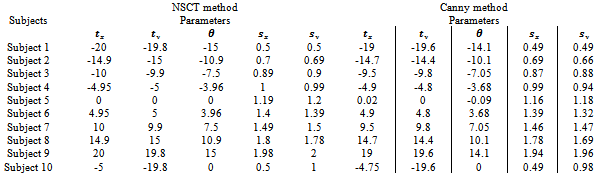
were bounded in the following way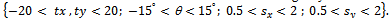 Registration results: the parameters of affine transformation matrix output from two registration systems were listed in Table 2.In this test series, two registration systems provided accurate registrations for single subject with image sources from same modality. However, for canny edge extraction and NSCT edge extraction, good initial search location needs to be provided within the normal range of misregistration.
Registration results: the parameters of affine transformation matrix output from two registration systems were listed in Table 2.In this test series, two registration systems provided accurate registrations for single subject with image sources from same modality. However, for canny edge extraction and NSCT edge extraction, good initial search location needs to be provided within the normal range of misregistration.
|
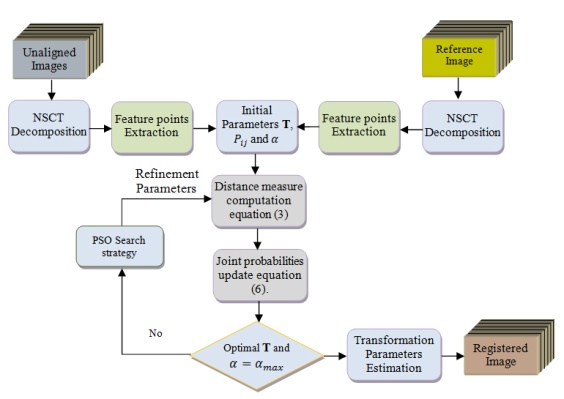 | Figure 3. The proposed feature-based image registration algorithm |
|
|
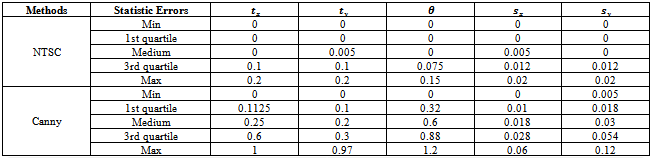
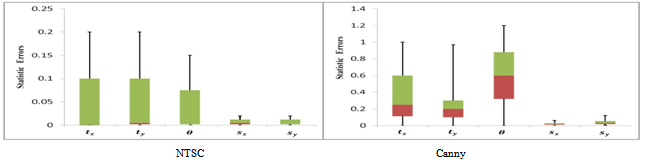 | Figure 5. Box and whisker plot of the statistic errors across all tests of medical images (feature-based method) |
5. Conclusions
- In this paper, we have introduced a MRI monomodal registration, which are employing NSCT transform and mutual information. In this test series, two registration systems provided accurate registrations for a single subject with image sources from MRI images monomodal. However, for Canny edge extraction and NSCT edge extraction, good initial search location needs to be provided within the normal range of misregistration. As a result, the registration performance was giving promising results, as indicated in Figure 5. The proposed one has the lowest mean and median among all measures, indicating that the proposed NTSC-based perform better than traditional Canny edge-based method. The speed of searching for the optimum value is also improved after using PSO. According to the experiments, we can conclude that the method proposed is maintaining good performance; however, experiments show that our method works well for monomodal medical image registration. We have only considered the two-dimensional registration. Our further work is to apply the method to three-dimensional registration.
ACKNOWLEDGEMENTS
- Part of this work is supported by USM Research University grant No. 814012.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML