1. Introduction

The development of modern society has always focused on creating new devices i.e. an assembly of components designed for a specific function. Each part performs a simple action so that the entire unit can achieve a more complex but useful purpose.

The molecular-level device can be defined as an assembly of a number of molecular components[1]. As Richard Feynman stated in his talk to the American Physical Society in 1959, “there is plenty of room at the bottom.” The miniaturization of components has opened a path to new technologies in medicine. Starting from the bottom-up, there has been some progress in the construction of “smart” nanoparticles for targeted drug delivery as well as for cancer therapy[2-5].The fullerene family, and especially C₆₀, was actively used in a biological domain. Water-soluble C₆₀-derivatives have been actively explored. However, the application of fullerenes for drug delivery is still in infancy. The design and synthesis of multifunctionalized C₆₀-based systems able to penetrate cell membranes and deliver active agents is an attractive challenge[6]. Gupta and Gupta demonstrated in 2005[7] that magnetic iron oxide particles may be used as a core. Following wild hype and some fantasy, a general arrangement for a therapeutic nanodevice consisting of a magnetic core, organic layer, sensors and actuators, such as affinity polypeptides was determined[8-10]. Zhao and co-workers[11] studied the structural transformations of metallofullerene Gd@C₈₂ under various circumstances. It was found that the Gd@C₈₂ was fully collapsed at 580°C, which was lower than that for the complete destruction of C₆₀. The authors ascribed the easier decomposition to an encapsulated metal in the carbon cage that could induce a deformation of C–C bonds. To release drugs from a fullerene cage, an anisotropic magnetic core changing its own orientation under an external magnetic field could have been used[12].

Among the diverse features of fullerenes, redox properties, which are particularly attractive to biomedical applications, have been extensively studied[13, 14]. Various types of C₆₀ functionalization that provide hydrophilicity of fullerenes have been reviewed[13]. Such fullerenes may accumulate in tumors[15]. Some studies also have reported that fullerenes can cross the blood-brain barrier[16, 17]. The Gd@ C₈₂(OH)₂₂, a water-soluble endohedral metallofullerene derivative, has been proven to possess antineoplastic activity in mice. Studies of the nanoparticles in vitro have demonstrated a low or absent toxicity in mice and C.elegans. The Gd@C₈₂(OH)₂₂ complex is tolerated by worms and has no toxic effects on longevity, stress resistance, growth and behavior of C.elegans[18].

Like art, where aesthetic design principles discovered by Michelangelo in XVI century; the golden mean, balance, proportion, rhythm, repetition, emphasis, unity, symmetry and asymmetry, nanotechnology requires a set of basic building blocks and assembly rules based on the natural principles of the nanoworld[1]. Among carbon species, such as carbene complexes of transition metals, intermediate transition metal carbides, endohedral metal fullerenes, and graphite intercalation compounds, some structures are impossible. In this case, computer simulation gives rise to design novel biologically compatible nanomagnets.

In this manuscript, an effort has been made to discover “design principles” using ab initio computer simulations to engineer carbide and metallofullerene nanoparticles as a platform for bio-compatible materials. Trigonal-bipyramidal Co₅ and icosahedral Co₁₃ magnetic clusters covered by carbon atoms in different positions, as well as the Co₅ and Co₁₃ clusters embedded into fullerenes C₆₀ and C₈₀ with I_h point group symmetry were used in computational experiments. The intention of this project is to improve understanding at an atomic level and as a step toward the major goal of designing nanostructures from the bottom up.

2. Computational Details

Atomic coordinates of pre-optimized Co₅ and Co₁₃ magnetic clusters were obtained from[19]. Co₅ and Co₁₃ metallic clusters were covered by carbon atoms using Avogadro v.1.0.0 molecule editor[20] or Chem3D Ultra v.8.0.3 molecular modeller and analyzer[21]. Atomic coordinates of fullerenes were downloaded from the Mitsuho-Yoshida's Fullerene Library database[22]. Molecular structures of the fullerenes were combined with Co₅ and Co₁₃ clusters by SPDB viewer v.4.1[23].

Atomistic quantum chemistry calculations were performed employing Density Functional Theory (DFT)[24], which was implemented within the OpenMX v.3.5 Software[25-28]. The calculation of atomic structures was done using local spin density approximation of Ceperley-Alder (LSDA-CA)[29] or by the Perdew-Burke-Ernzerhof generalized gradient approximation (GGA-PBE)[30] with parameters fitted to d-orbitals of cobalt atoms. Structural relaxation was performed by stepwise decent optimization (SDO) or by direct inversion iterative sub-space optimization (DIIS)[31]. The atomic species were defined as C4.0-s1p1 and Co5.5-s2p2d2f1[32] with energy cutoff 200.0 Ryd, while the energy convergence criterion (SCF) was set at 10^-4 Hartree during the fitting procedure. An electronic temperature in experiments was 300.0 K. Spin polarization was switched on and the total spin magnetic moment (µ_B) was calculated. The energy formation E_form of experimental complexes was estimated as described in[12].

3. Results

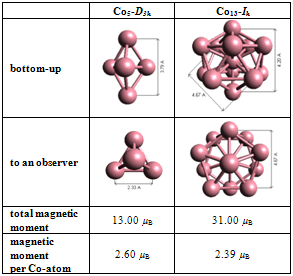
Properties of pure Co₅-D_3h and Co₁₃-Ih clusters

The Co₅-D_3h magnetic cluster was chosen for the experiments because it is the most stable structure with anisotropic properties and has the smallest trigonal bipyramid geometry that demonstrates the highest magnetic moment per atom, 2.6 µB, among small Com clusters (m = 2-20)[33]. The Co₁₃-Ih cluster was selected because it is the smallest magic structure with icosahedral symmetry, including two pentagonal rings, two apex atoms and a central atom with a large total magnetic moment 31.0 µB[33, 34].

According to our calculations, the pure Co₅ cluster with the average Co–Co bond length 2.33 Å and a distance of 3.80 Å between cobalt atoms on the opposite vertices of trigonal bipyramid demonstrated the total magnetic moment 13.00 µ_B. After structural optimization, the pure Co₁₃ cluster showed an average bond length of 2.38 Å, as well as space up to 4.20 Å between apex atoms and a remoteness of 4.67 Å between atoms on the opposite vertices of two pentagonal rings of the icosahedron with the total magnetic moment at 31.00 µ_B (Table 1). Normalization that we used to express experimental data allowed comparison of results obtained by other authors. The magnetic moments for Co₅ and Co₁₃ clusters in an amount of 2.60 and 2.39 µ_B/atom respectively are consistent with[33, 35, 36] and higher than hcp bulk value 1.72 µ_B[37].

Table 1. Co5 and Co13 clusters in various orientations and their characteristics

Reduction of the magnetic moment during an addition of C-atoms and the effect of saturation

Artificial carbides demonstrated stability in simulation at 300 K. The absolute value of the total energy for Co_mC_n complexes increased monotonically with the rising number of carbon atoms independent of the method of calculation[38]. The average length of Co–C bond stabilized at 1.68 Å after 100 steps of MD optimization in the case of Co₅C₅ carbide. When we placed carbon atoms one by one on the Co₅ cluster, the total magnetic moment of the carbide complex dropped to 11.00 µ_B (84.6 %) for Co₅C₁ and linearly decreased. There was an increased number of carbon atoms on the surface, which retained for the Co₅C₅ complex only 23.1% (3.00 µ_B) of initial activity of the pure cobalt cluster. The slope of the normalized linear trend was k₁ = –0.40 (see Fig. 1a). In contrast, magnetic moments of Co₁₃C_n particles decreased slowly through the slope k₂ = –0.21 with an increasing number of carbon atoms n such that from 87.1 % (total value 26.93 µ_B) for Co₁₃C₁ complex to 29.1 % (total value 9.01 µ_B) for Co₁₃C₈ complex, and remained steady at 28.7 % until n = 12 (see Fig. 1b). As indicated, LDA and GGA approximations showed similar results (R_LDA/GGA = 0.99) although SDO optimization was smoother than DIIS optimization with standard errors of DFT calculation and correlation R_SDO/DIIS = 0.95[38].

Asymmetric effects of carbon atoms on magnetism of Co clusters

In the following experiments, we examined various arrangements of carbon atoms on the surface of cobalt clusters starting simulations from different conformations of isomers for Co₅C₅ and Co₁₃C₁₂ carbides (see Table 2). We found the absolute value of total energy for the compounds grew with increasing structural complexity and loss of symmetry. Magnetic moments of isomeric forms for carbide Co₅C₅ improved by the reducing Co–C bonds and the raising the asymmetry of allocation of carbon atoms on the surface of the cobalt cluster. This tendency began at 3.00 µ_B (23.1 %) for the trigonal-bipyramidal Co₅ cluster fully covered by five C-atoms in a highly symmetric way, continued to 5.00 µ_B (38.5 %) for a capped Co₅ cluster and finished at a value of 11.00 µ_B (84.6 %) for Co₅ cluster with an attached chain of five carbon atoms (Fig. 2a). Each experiment was done five times with different initial molecular conformations of Co₅C₅ isomers and resulted in similar outputs; the average standard deviation was d₁ = 0.0004 µ_B.

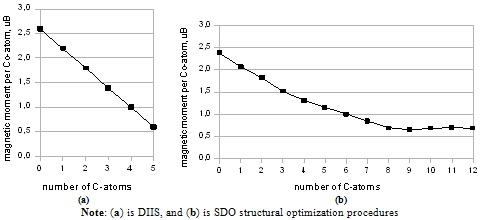Figure 1. Magnetic moment of carbides Co5Cn (a) and Co13Cn (b) depending on the number of carbon atoms

Table 2. Examples of isomers for Co5C5 and Co13C6,12 complexes with the average total energy in Hartree

To find out whether the asymmetric distribution of carbon atoms on the cobalt cluster is significant in magnetism, we eliminated the role of the number of metal-carbon bonds in the following experiments using the icosahedral Co₁₃ cluster with attached six or twelve carbon atoms in six different sites. The Co₁₃ cluster covered by six carbon atoms in a highly symmetrical mode demonstrated a total magnetic moment of 16.67 µ_B (53.8 %). When an asymmetric blueprint with the six Co–C bonds was used, the magnetic moment increased to 19.00 µ_B (61.3 %). When the Co₁₃C₁₂ complexes were applied, as in the previous case, the capped carbide Co₁₃C₁₂ with the six Co–C bonds exposed improved magnetic characteristics in comparison with its geometric symmetrical isomer i.e. 29.97 µ_B (96.7 %) versus 28.20 µ_B (91.0 %) respectively (Fig. 2b). On the other hand, the fully covered carbon isomer of Co₁₃C₁₂ showed minimal magnetism at 7.00 µ_B (22.6 %). These experiments revealed a minor role of asymmetry in addition to the number of Co–C bonds in the magnetism of carbides.

Note: the average standard deviation d₂ = 0.0521 µ_B was much larger for more complex carbides assuming Co₁₃ metallic cluster than for simple Co₅C_n carbides. Bearing this in mind, we considered investigating endohedral fullerenes more closely.

Experiments on fullerenes with Ih point symmetry

The absolute rate of binding energy for endohedral complexes Co_m@C_n grew with the size of cluster m and the size of fullerene n, such that the energy of complex formation E_form for Co₅@C₆₀ was –0.305 Hartree, for Co₅@C₈₀ was –0.486 Hartree, and the same feature for Co₁₃@C₈₀ was –0.713 Hartree. The negative values of binding/formation energies was evidence that the process of complexation of these composites should be exothermic.

Buckyball C₈₀-I_h decreased the magnetic activity of pure Co₅ cluster to 11.78 µ_B (90.6 %); however, C₆₀-I_h provoked a more significant reduction of the magnetic moment to 10.47 µ_B (80.5 %) (Table 3). The average distances between Co- and C-atoms were 2.18 and 2.33 Å for Co₅@C₆₀ and Co₅@C₈₀ complexes respectively. What was interesting that the endohedral fullerene Co₁₃@C₈₀ demonstrated the highest total magnetic moment 27.00 µ_B; nonetheless, that only 87.1 % of the magnetic activity of a pure Co₁₃ cluster remained. The internal space of the fullerene C₈₀-I_h was filled by the Co₁₃-I_h cluster which formed multiple Co–C bonds to fullerene cage with the average distance of 2.09 Å.

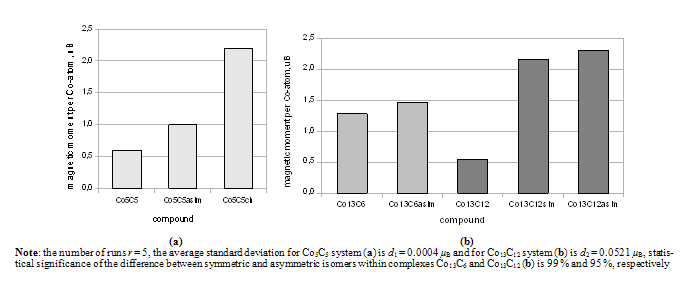Figure 2. Magnetic moments of isomers of Co5C5 (a) and Co13C6,12 (b) complexes

Table 3. Characteristics of endohedral metallofullerenes

We found within the experimental data set that the average Co–C bond length of a complex correlated with the magnetic moment per one cobalt atom (R₁ = 0.99458). Furthermore, strong linear correlation (R₂ = 0.99998) was discovered for the dependence

(1)

where M is the magnetic moment per Me-atom of a given complex (µ_B), L_i is the length of the Me–C bond i (Å), and N is the total number of Me–C bonds in the complex.

It was remarkable that the longest distances between Co- and C-atoms, as well as rare Co–C bindings, provoked in the Co₅@C₈₀ complex a minimal silencing of magnetism related to the reference, pure Co₅ cluster. These data confirm previous results i.e. 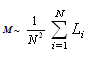the magnetic moment is strongly correlated to the effective hybridization between d-electrons of core transition metal cluster and π-electrons on the carbon shell, which is closely related to the average bond length and the number of bonds[12, 33, 35, 36, 39-41].

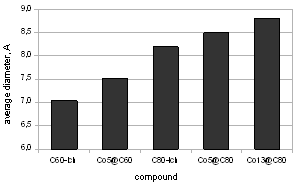Figure 3. The size of a fullerene cage based on the metal cluster insertion

Following the idea that sharing electrons between metallic cluster and carbon cage leads to the formation of molecular orbitals with coupled electrons and to the reduction of spin magnetic moment, we investigated the structural characteristics of Co_m@C_n complexes in more detail to confirm this interaction. We observed some structural transformations of carbon cage and metallic core for endohedral complexes in comparison with native fullerenes and metal clusters. For instance, fullerenes C₆₀ and C₈₀ with I_h point group symmetry resembled spheres with diameters of 7.04 and 8.20 Å respectively. However, in our experiments, the carbon cages of endohedral metallofullerenes presented distorted spheres following a geometry of the internal metallic cluster, such that the average diameter of Co₅@C₆₀ was 7.51 Å, the diameter of Co₅@C₈₀ was 8.50 Å, and for Co₁₃@C₈₀ it was 8.82 Å (Fig. 3). The geometry of metallic core was also slightly changed in comparison to the initial ground state (Table 1). The Co₅ cluster, confined by fullerene C₆₀, exposed a distance 3.40 Å between cobalt atoms on the opposite vertices of compressed trigonal bipyramid and the average Co–Co bond distance of 2.34 Å. The same Co₅ cluster within fullerene C₈₀ showed distorted geometric characteristics, such as 3.82 Å and 2.36 Å respectively. In addition, the embedded Co₁₃ cluster demonstrated a distance 5.04 Å between the apex atoms and an expense 4.81 Å between the atoms on the opposite vertices of pentagonal rings of the deformed icosahedron, as well as an average bond length of about 2.45 Å (Table 4).

On the whole, the volume of a carbon cage increased as a result of cluster encapsulation, which depended visibly on the range of metallic core in the case of fullerene C₈₀. The size of metallic core also increased in a large carbon room but decreased when the atomic environment was narrow as in the case of Co₅ cluster embedded into fullerene C₆₀.

Table 4. Geometric properties of Co5 and Co13 clusters in different environments in vacuum in C60 in C80 Co5 3.794 / 2.327 3.396 / 2.336 3.820 / 2.356 Co13 4.200 / 2.380 - 5.037 / 2.452 Note: distance between apex atoms / average bond length, Å

4. Discussion

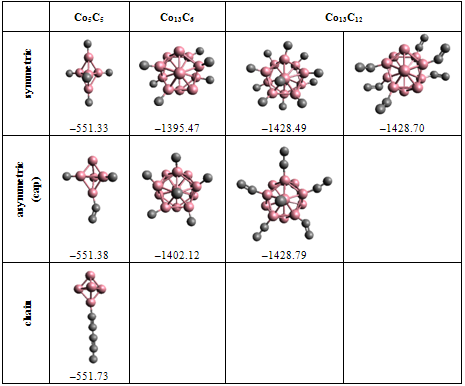
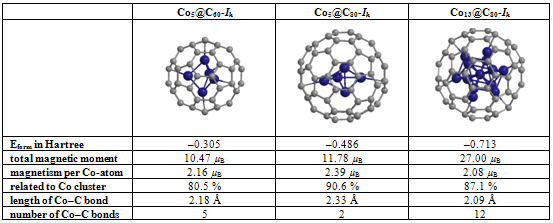
Many scientific phenomena are investigated by computer models. Computer experiment is a number or runs of the code with various inputs[42]. We proved the utility of computational experiments to elucidate key features of interaction between Co-atoms and organic environment. Metallic clusters with a large magnetic moment were chosen because magnetic nanoparticles should be manipulated by an external magnetic field during the magneto-thermal cancer treatment[4]. We performed a study of magnetism according to the geometry of clusters and carbon shell. The properties of nanostructures depended on how atoms are organized.

Asymmetric magnetic carbides

Although pure Co₁₃ cluster demonstrated a higher total spin magnetic moment (31.00 µ_B) than a pure Co₅ cluster (13.00 µ_B), the magnetic moment per atom was bigger for Co₅ than for the Co₁₃ cluster, i.e. 2.60 versus 2.39 µ_B respectively (Table 1), which might be significant for tiny magnetic devices. Here, we described a negative effect of the carbon environment on magnetism for Co clusters. Magnetic moment of the clusters decreased monotonically with an increasing number of attached C-atoms. Nevertheless, covalent binding of carbon atoms to the surface of cobalt clusters did not suppress the magnetism totally. Still Co₅C₅ complex showed 23.1 % of initial activity of pure Co₅ cluster, and Co₁₃C_8-12 presented about 28.7 % of magnetism of Co₁₃ cluster (Fig. 1).

We used molecular complexes of cobalt carbides and their isomers with stable energetic characteristics (Table 2) in experiments on various initial conformations of the complexes; the dissimilar outputs were analyzed and a difference in magnetic moments was found. That is substantial in that the average standard deviation of magnetic moments was about 130 times larger for Co₁₃C₁₂ system than the deviation for Co₅C₅ system. This spread might have been because the number of local minima in a potential energy surface increases very rapidly with the number of atoms in a complex.

Surprising effects were observed in experiments with asymmetric localization of carbon atoms on the surface of cobalt clusters. When we removed part of the carbon atoms from the surface of Co_mC_n complexes and added them to the rest of the attached carbon atoms, actually building short carbon chains, the magnetic moment grew for both Co₅C₅ and Co₁₃C₁₂ carbides (Fig. 2). This effect could be explained by the reduction of the number of Co–C bonds and the increase in the number of unpaired d-electrons with uncoupled spins, which contribute to the total spin magnetic moment[39]. However, it is difficult to realize the arrangements of electrons in details. Why does a simple shift of carbon atoms to one side of the cobalt cluster increase magnetism? In this case, the π-electrons of double C=C bonds might interact with each other on the cap of a carbide particle.

Nanomagnets based on the endohedral metallofullerenes

Several attempts have been made to formalize aspects of interaction metallic clusters with fullerenes[40, 41]. The position effect of Co₅ cluster within an elongated fullerene C₇₀-D_3h was published in[12]. Here, we interested in the future discovery of “design rules” at nanosclae. Drawing from recent data and our own results, we proposed a simple model to estimate the magnetic moment based on the length and the number of Me–C bonds (1). We suppose that magnetism of endohedral fullerenes depends directly on the average length of Me–C bond and is in reverse dependence with the number of bonds.

Among investigated endohedral fullerenes, the Co₅@C₈₀ complex provided the highest magnetic moment per cobalt atom of 2.39 µ_B, resembling 90.6 % activity of pure Co₅ cluster, with the minimal number and maximal distance of Co–C bonds (Table 3). The size of the complex was about 8.50 Å (Fig. 3), the deformations of Co core were negligible (Table 4), which will be attractive for biological applications.

We also note that the hydrated derivative Gd@C₈₂(OH)₂₂ used in many biological studies[43, 44], resembles endohedral metallofullerene Co₅@C₈₀. Based on the computational studies, we suppose that the Co₅@C₈₀ might be a prospective platform for magneto-thermal cancer therapy and developing novel treatment approaches for humans.

Remaining problems

The current state-of-the-art technology is still not able to provide full computer added design and engineering of new functional materials from the atomic level up[45]. The lack of a broadly applicable theory across multiple scales leaves the design of magnetic nanoparticles incomplete. To date, a “designer” needs to use different and separate tools and approaches to meet a required goal.

Although we studied molecular structures of growing complexity from carbides to metallofullerenes in the frame of OpenMX software, our attempt to investigate Co13 cluster in 1PRN barrel protein from the bacteria R.blastica was unsuccessful (data not present). This example calls for effective DFT/MD coupling and the search for new numerical methods such as time-dependent DFT, application of Green’s function techniques, and completely innovative approaches to soft matter systems. To answer questions about how to design, analyze, and build molecular devices, development of theoretical nanoscience is needed as well as libraries of primitives for bottom-up engineering on a nanometer scale, knowledge about building blocks, an addressable platform to combine those primitives in a desirable way[46], a proof-of-principle for much larger composed systems, and the efficient combination of experiments to prove the point of view.

5. Conclusions

The trends obtained from our DFT study give a qualitative understanding of magnetism at the atomistic level. It has been shown that carbon atoms decreased the magnetic moment of cobalt clusters; the pattern of distribution of C-atoms on the surface of Co clusters played an important role in the magnetic properties of a whole cobalt-carbon system, depending generally on the number of metal-carbon bonds and the length of interatomic distances that also possibly provided a charge transfer from metallic cluster to carbon cage. As we have seen, magnetism at nanoscale is very sensitive to an atomic environment. The more crowded the carbon environment for a metallic core, the less the magnetic moment of the metal-carbon complex.