1. Introduction

Tissue engineering is an emerging field with the aim of repairing or creating new tissues. It is evident that the scaffold plays a critical role in forming the required constructs in a bioreactor[1]. In bioreactors, biological and biochemical processes occur under closely monitored and tightly controlled environmental or operating conditions. As such, bioreactors play a significant role in the in vitro experiments of tissue engineering[2]. The perfusion bioreactor, in which the culture medium continuously flows through the pores of the scaffold, is superior compared to other bioreactors (e.g. the spinner flask bioreactor and the rotating wall vessel bioreactor) since mass transfer is enhanced within the scaffold. The scaffold in a perfusion bioreactor can have adequate nutrient supply, timely waste removal, and sufficient gaseous exchange, thus promoting cell growth and proliferation within the scaffold[3]. However, increased flow rates can create large shear stresses on the scaffold, which can in turn wash away the attached cells, adversely influence the cellular metabolism, and evendamage the cells. It is noted in the literature[4,5] that amoderate shear stress ishighly beneficial to the formation ofglycosaminoglycan (GAG) and thus cartilage tissues. Therefore, a compromise between the mass transfer and the shear stress must be made in the cell culture for a given application.

Due to the lack of adequate sensors, it is difficult, even impossible, to measure the local shear stress distribution within a scaffold[6]. Computational fluid dynamics (CFD) shows promise in solving this problem. CFD has been widely used in various fields because it often requires less time and fewer resources than experiments. In tissue engineering, CFD has recently shown promise in visualizing the flow phenomena within bioreactors, thus providingthe detailed information and insight, which would be difficult to gain by experiments.

The local volume average approach is one method to evaluate the average shear stress in a porous media, for which specific mathematical modelsarerequired[6]. The limitation of this method is that only the averaged shear stress, rather than its distribution, can be obtained. To overcome this limitation, various approaches have been developed and reported in the literature, though at their early stage.In the earliest studies, scaffolds were treated as impermeable constructs in the development of CFD models. Based on simulation results, improved designs for bioreactors and scaffold constructs were reported[7-10]. In the following studies, the scaffold structure was taken into consideration in the model development. For scaffolds with irregular structures such as those fabricated by means of conventional fabrication methods, micro-computed tomography (μCT) was used to create 3-dimensional (3D) geometric models[3, 11-13]. In addition to μCT, another method to deal with irregular geometry is to treat the inner structure as a repetitive pattern of units by means of computer-aided-design (CAD) methods. The shear stress distribution in such a unit has been studied with a focus on identifying the effect of pore size and porosity on it[6, 11, 14]. In these studies, the scaffolds with irregular internal structures were significantly simplified in the model development, thus causing to the errors in the following simulation. Currently,scaffolds manufactured by rapid prototyping (RP) techniques have shown promising in various tissue engineering applications due to their controllable microstructure[15, 16] For such scaffolds, the structure is regular and the geometry can be readily modelled by CAD methods. Singh et al.[17, 18] utilized commercial CFD software to create models of such scaffolds in bioreactorsand studied the influence of mechanical stimuli on the velocity and shear stress distribution. Unfortunately, their studies were limited to non-perfusion bioreactors.

In this research, scaffolds with a regular structure, such as those fabricated through the RP technique, are modelled under both perfusion and non-perfusion situations. This studyaims to represent the flow field within the scaffold and to identify the influence on the wall shear stress distribution of the controllable parameters in scaffold fabrication and cell culture process.

2. Methodology

2.1. Bioreactor Configuration

Both the perfusion and non-perfusion bioreactors considered in this study are shown schematically in Figure1, with thedifference in the inlet and outlet locations. A cell seeded tissue scaffold is placed between the two struts and the chamber allows for circulation of the fluid medium. A perfusion system occurs when the inlet flow comes directly through the channel inside the struts and enters the bottom surface of the scaffold (Figure 1(a)). A non-perfusion system occurs when the inlet is located at the wall of the chamber (Figure 1(b)). In the present study, the inlet diameter is 10mmand the height, length and width of the chamber are 140, 50 and 50 mm, respectively. Taking advantage of the symmetry of the chamber, only one-fourth of the bioreactor chamber is modelled to reduce the computation needed.

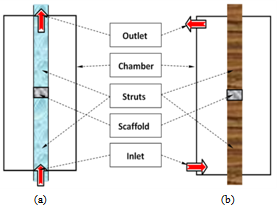Figure 1. Schematic of bioreactors: (a) perfusion bioreactorand (b) non-perfusion bioreactor

2.2. Scaffold Used for Model Development

The structure of the scaffolds for the model developmentis shown in Figure 2, in which the strand diameter (D) and the horizontal span(Y) can be controlled during the scaffold fabrication [16, 19]. Also shown in Figure2 are the distance between two adjacent horizontal (h_xy) and vertical (h_z) strands, which together represent the pore size. While both the vertical pore size (h_z) and the horizontal distance (h_xy) are associated with the strand diameter (D) and the horizontal span (Y), respectively, the vertical pore size (h_z) is also affected by the scaffold material properties due to the fusion of the two strands. Based on the previous research in our group [16], the vertical pore size (h_z) is determined by the diameter of the strand (D), the density of the scaffold material (ρ), the elastic limit stress (τ_e), the horizontal span (Y) and the angle between the two layers (θ) (Figure 2). The approximate relationship can be described as follows:

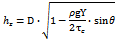The values of the density (ρ) and elastic limit stress (τ_e) are different for different scaffold materials. In the present study, a chitosan solution with 40% hyroxylapatite (HA) gel is assumed to be used for the scaffold fabrication and its elastic limit stress (τ_e) is 11.0 Pa as identified in [16]. In the present study, the strand diameter D was varied from 0.2 to 0.4 mm, while the horizontal span Y was varied from 0.5 to 0.9 mm.The corresponding vertical pore sizes are given in Table 1. With this information, the geometric model was constructed in SOLIDWORKS. From the geometric model, the porosity, which is defined as the ratio of the void volume to the total volume, was calculated for each scaffold. The calculated porosity values are also listed in Table 1.

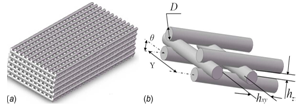Figure 2. Geometric parameters for tissue scaffold

Table 1. Pore size, hz, and porosity, ε,for different scaffolds Horizontal Span, Y Strand Diameter, D 0.2 mm 0.3 mm 0.4 mm hz (mm) ε (%) hz (mm) ε (%) hz (mm) ε (%) 0.5 mm 0.179 66.9 0.268 49.9 0.358 34.0 0.7 mm 0.170 75.8 0.255 63.9 0.340 51.7 0.9 mm 0.160 80.6 0.240 71.3 0.320 61.2

2.3. Computational Method

When a tissue scaffold is submerged in the fluid environment within a perfusion reactor, the fluid not only flows around the outside of the scaffold but also within the scaffold itself. The fluid deformation then results in the development of fluid stresses: of specific interest in this study are the shear stresses exerted on the surface of the strands of the scaffold which can be considered as the shear stress on the attached cells. The model geometry created in SOLIDWORKS was imported into the commercial CFD package ANSYS-CFX, which was used to solve the Navier-Stokes equations to determine the velocity field and also the shear stress exerted on the scaffolds. In this case, the flow was treated as three-dimensional, incompressible flow of a Newtonian fluid.

CFX-Mesh as used to create three unstructuredmeshes with 284681, 622261 and 1142781 elements, respectively. The difference in the calculated maximum wall shear stresses between the last two meshes was approximately 1.5%. Therefore, the mesh with 622261 elements, shown in Figure 3(b), was assumed to be fine enough to accurately determine the flow field. The simulation used a non-uniform unstructured mesh or grid in which the element size was varied for different parts of the bioreactor. Local grid refinement was used to resolve the tissue scaffold geometry, as shown in Figure 3(c). Near the scaffold surface, the grid size ranged from 0.1to 0.12mm, while the maximum grid length near the wall of the bioreactor chamber was 7 mm.

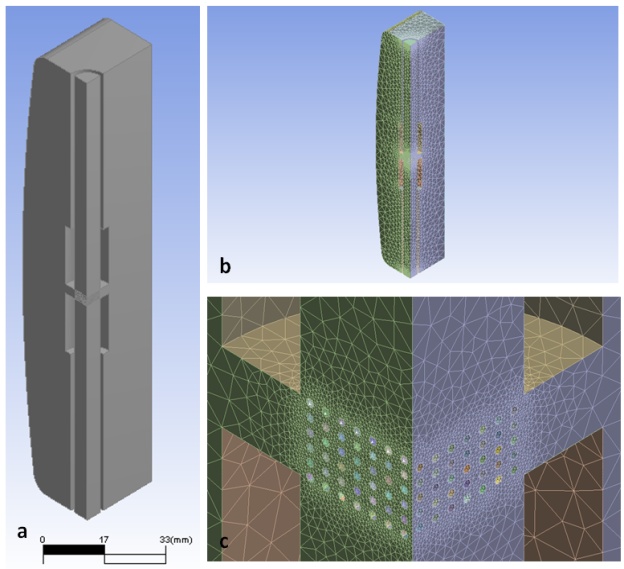Figure 3. a)Geometric model, b) mesh, and c) refined mesh around tissue scaffold

2.4. Boundary Conditions

As show previously in Figure1(a), for a perfusion bioreactor, the fluid enters the scaffold through the bottom strut. A constant mass flow rate boundary condition was specified at an inlet section located upstream of the scaffold within the supporting strut. In this way, the flow can develop within the channel inside the channel to simulate the actual experimental condition. Note that the internal flow can connect with the fluid outside the scaffold through the open channels of the scaffold, and in this way, the internal fluid creates a small disturbance in the fluid contained in the bioreactor. The outlet was placed at an exit plane located within the channel inside the strut.In this case, the average pressure at the outlet was set to zero. The walls of the chamber, the struts and the scaffold were assumed to be no-slip, solid walls.

The simulations were first performed for a scaffold with D = 0.3 mm and Y = 0.7 mm. To investigate the effect of flow rate, three different flow rates were considered: 0.05ml/min, 0.10ml/min and 0.15ml/min. In order to assess the effect of geometry, additional simulations explored scaffolds in which the strand diameter (D) and horizontal span (Y) were independently varied, as shown in Table 1.

3. Results and Discussion

3.1. Comparison of Flow Field for Perfusion and Non-perfusion Bioreactors

Simulations were initially carried out for a tissue scaffold with a strand diameter of D = 0.3 mm and horizontal span of Y = 0.7mm, for the case of both perfusion and non-perfusion bioreactors. Figure4 shows the simulation results for the case of the perfusion bioreactor. In this figure, it is seen that the majority of the streamlines go through the tissue scaffold, implying that there is strong perfusion inside the scaffold. In contrast, Figure 4(a) shows that there is minimal fluid motion in other areas of the bioreactor. As a result, the strong perfusion produces relatively high shear stresses on the surfaces of the strands in some regions of the scaffold as shown in Figure4(c). The shear stress typically is larger near the outer edge of the scaffold. This suggests that when seeding cells, one strategy might be to seed more cells in the centre area of the scaffold to avoid the regions of highshear stress created by the perfusion flow.

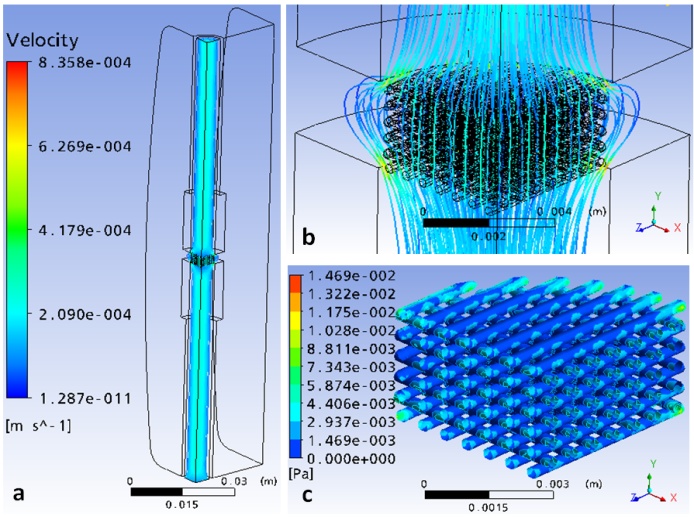Figure 4. Simulation results for the scaffold with D=0.3mm and Y=0.7mm in a perfusionbioreactor: a) velocity streamlines in bioreactor, b) velocity streamlines around the tissue scaffold, and c) surface shear stress distribution in the scaffold

To better highlight the flow characteristics of a perfusion bioreactor a simulation of the same scaffold in the non-perfusion bioreactor, was carried out as shown in Figure 5. Recall that for the non-perfusion bioreactor, the inlet and outlet were located in the wall of the bioreactor chamber, as shown in Figure 1(b). It is seen from Figure 5(a) that the flow occurred throughout the bioreactor. For the relatively low velocity levels near the scaffold, the shear stress in Figure5 (b) is almost zero.

Based on the comparison between Figure 4 and 5, it is seen that in the perfusion bioreactor, the convection and hence mass transfer enhanced, which also results in increased levels of shear stress on the internal walls. These results suggest that for cell culture, the most suitable bioreactor depends on the specific situation and cell type. For example, if the cells require more nutrients and growth factors during the cell culture process, the perfusion bioreactor is more effective; however, the non-perfusion bioreactor is a safer choice if the cells are especially sensitive to the shear stress level. If the perfusion bioreactor is used, then the flow rate must be set to ensure acceptable levels of wall shear stress within the scaffold. In this context, the factors which affect the shear stress distribution and magnitude are considered in the next section.

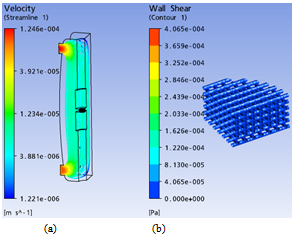Figure 5. Simulation results for the scaffold with D=0.3mm and Y=0.7mm in a non-perfusion bioreactor: a) velocity streamlines, and b) wall shear stress distribution in the tissue scaffold

3.2. Flow Field within the Scaffold in the Perfusion Bioreactor

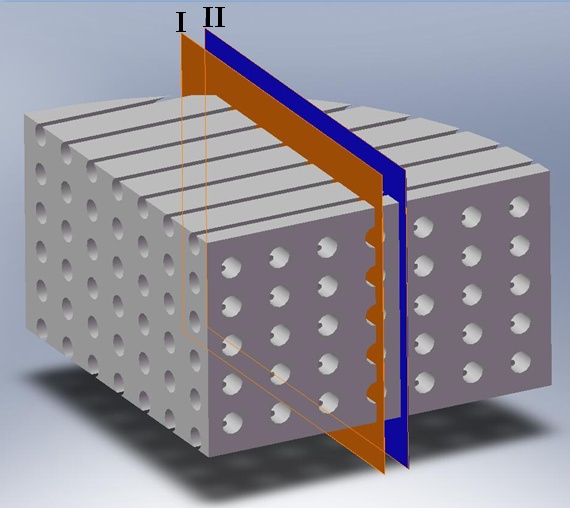Figure 6. The location of the two sections used to visualize the flow

With the help of CFD, the flow field within the internal pores of the scaffold can be captured. The average velocity in the scaffold is 3.4768×10-4 m/s and the average Reynolds Number based on the diameter of the scaffold strand is 1.17×10-2. In order to illustrate the details of the fluid motion within the scaffold, the velocity fields for cross-sections at two different locations were investigated. As shown in Figure6, section I is a plane section through the scaffold strand and represents the flow which is blocked by the scaffold strands; section II represents a planesectionlocated between the two lines of strands and hence represents the flow which has a direct path through the scaffold channel. The simulation results presented below are for the case in which D=0.3mm and Y=0.7mm.

To visualize the local flow, the velocity vectors in section I and section II are presented in Figure 7(a) and (b), respectively. Note that small arrows are used to show the local flow directions and the colours represent the magnitude. For section I, due to the obstruction of thescaffold strands, fluid is squeezed out near the lateral surfaces of the scaffold, especially near the top and bottom of the scaffold, which are also the locations of enhanced velocity. Some fluid is observed to exit the scaffold and then re-enter the scaffold prior to exiting the outlet channel of the bioreactor located within the strut. For section II, the open channel within the scaffold provides a direct passage for the perfused medium.The local velocity magnitude is shown by colour contours in Figure7 (c) and (d) forsection I and section II, respectively. From these simulation results, it is seen that due to the shielding provided by the scaffold strands in section I, the velocity in the area between two horizontal strandsis relatively low , implying that that this area would be suitable for cell attachment. In contrast, from Figure 7(d), it is clear that strong perfusion exists in the channel between two series of strands, which createsrelatively high local velocities. Based on a comparison between Figure 7(c) and (d), the region enclosed by the red line in Figure 7(c) would be a favourable area for cells to adhere due to the lower flow velocity levels. When seeding cells, if priority is given to seeding in this area, especially on the top and bottom walls of the strands, the cells will have less likelihood to be washed out by the perfused medium.

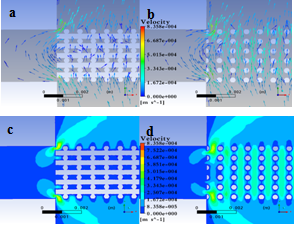Figure 7. Velocity distribution for two cross-sections at different locations within the scaffold: a) velocity vectors in section I, b) velocity vectors insection II, c) velocity magnitude in section I, and d) velocity magnitude in section II

3.3. Wall Shear Stress within the Scaffold in the Perfusion Bioreactor

The local wall shear stress within the scaffold can be affected by the scaffold geometric parameters including the strand diameterand the horizontal span as well as the flow rate of the circulated medium. Numerical simulations were performed for the cases presented in Table 1 and the results were compared to illustrate the effect of D and Y on the wall shear stress distributions. Figure 8 presents the discrete probability distribution for the magnitude of the wall shear stress for different values of D and Y. From the results, it is seen that the level of the wall shear stress values mostly appear in the bin centred on 1 mPa. With an increase in D (from top to bottom), the distribution tends to extend to higher pick values and the mean values also increases. Looking Figure.8 from left to right for a given value of D, with an increase in the value of Y, the wall shear stress has probability of appearing in the bin centred on 1 mPa. A similar conclusion can be drawn from Figure9, which shows the dependence of the average surface shear stress for scaffolds with different values of D and Y. This suggests that scaffolds with a smaller strand diameter can be used in cell culture in a perfusion bioreactor to limit the wall shear stress levels within the scaffold. Another summary conclusion is that so long as the mechanical strengthcriterion is satisfied, the horizontal span can be used to adjust the shear stress level within the scaffold. Specifically, for a given flow rate, a larger span will result in a reduction in the average shear stress level.

Figure 8. Distribution of surface shear stress for scaffold in perfusion bioreactor

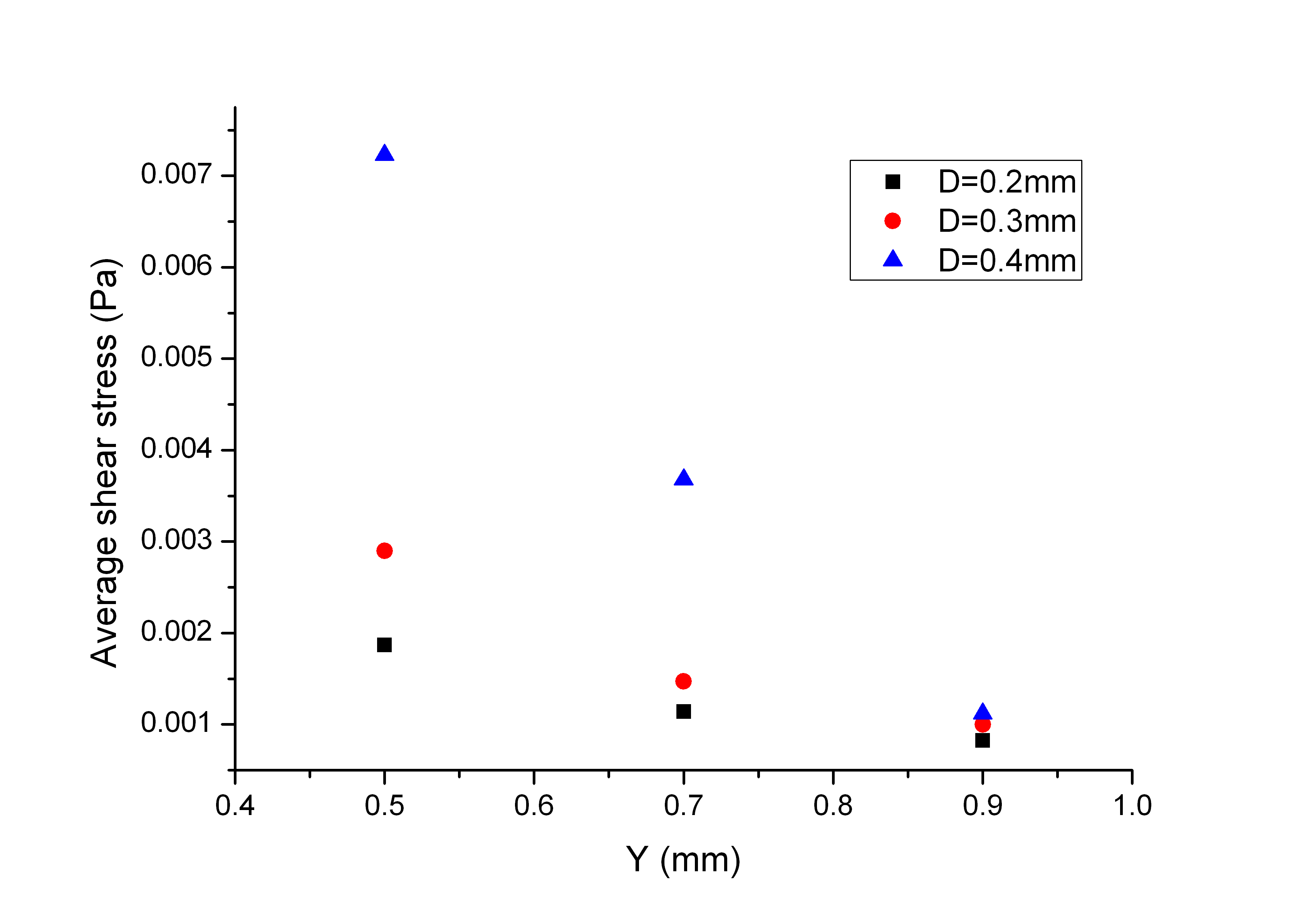Figure 9. Average shear stress distribution versus D and Y

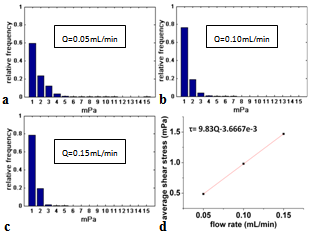Figure 10. Shear stress distribution within scaffold for different flow rates: a) Q=0.05 mL/min, b) Q=0.10 mL/min, c) Q= 0.15 mL/min, and d) average wall shear stress versus Q

4. Conclusions

The fluid flow inside and around a scaffold in a bioreactor is complex. This paper presents an investigation into such a flow within scaffolds cultured in both perfusion and non-fusion bioreactors, respectively. The simulation results demonstrate that the perfusion bioreactor provides a strong flow within the tissue scaffold, thus increasing the shear stress on the scaffold surface as compared to the non-perfusion bioreactor.The results also show that the value of the strand diameter and horizontal span can affect the shear stress generated on the scaffold. Generally, with an increase in the diameter, the shear stress level also increased; with an increase in the horizontal span, the shear stress decreased. The effect of flow rate, a controllable parameter in the cell culture process, was also investigated and it was found that the average shear stress level increased linearly with the flow rate.

The knowledge obtained from this research provides a quantitative insight into the velocity fieldand the shear stresses distributionwithin the scaffoldcultured in bioreactors. The effects of the controllable factors identified by the present study can be used to guide future scaffold design as well asexperimental studies.

ACKNOWLEDGMENTS

The authors would acknowledge the financial support from the Saskatchewan Health Research Foundation (SHRF) and the University of Saskatchewan (though a Graduate Scholarship to the first author) to the present study.