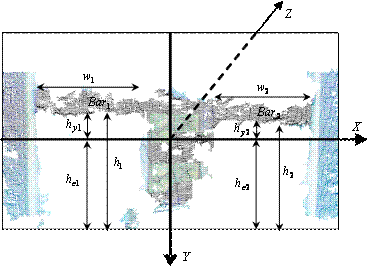
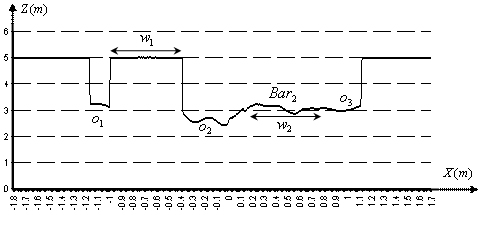
| [1] | Y. Adachi, K. Goto, Y. Matsnmoto, and T. Ogasawara, "Development of Control Assistant System for Robotic Wheelchair - Estimation of User's Behavior based on Mea- surements of Gaze and Environment," in Proceedings of the IEEE International Symposium on Computational Intelli- gence in Robotics and Automation, 2003, pp. 538-543 |
| [2] | L. M. Bergasa, M. Mazo, A. Gardel, R. Barea, and L. Boquete, "Commands generation by face movements applied to the guidance of a wheelchair for handicapped people," in Proceedings of the 15th International Conference on Pattern Recognition, 2000, pp. 660 - 663 |
| [3] | Y. Kuno, T. Yoshimura, M. Mitani, and A. Nakamura, "Robotic wheelchair looking at all people with multiple sensors," in Proceedings of IEEE Inter. Conf. on Multisensor Fusion and Integration for Intell. Sys., 2003, pp. 341 - 346 |
| [4] | I. Moon, K. Kim, J. Ryu, and M. Mun, "Face Direction-Based Human-Computer Interface using Image Observation and EMG Signal for The Disabled," in Proceedings of the IEEE Imter. Conf. on Robotic and Auto., 2003, pp. 1515-1520 |
| [5] | T. N. Nguyen, S. W. Su, and H. T. Nguyen, "Robust Neuro-Sliding Mode Multivariable Control Strategy for Powered Wheelchairs," IEEE Transactions on Neural Syst- ems And Rehabilitation Eng., vol. 19, pp. 105-111, 2011 |
| [6] | H. Seki, K. Ishihara, and S. Tadakuma, "Novel Regenerative Braking Control of Electric Power-Assisted Wheelchair for Safety Downhill Road Driving," IEEE Transactions on Industrial Electronics, vol. 56, pp. 1393-1400, 2009 |
| [7] | Y. Oonishi, S. Oh, and Y. Hori, "A New Control Method for Power-Assisted Wheelchair Based on the Surface Myoelect- ric Signal," IEEE Transactions on Industrial Electronics, vol. 57, pp. 3192-3196, 2010 |
| [8] | F. Chénier, P. Bigras, and R. Aissaoui, "An Orientation Estimator for the Wheelchair’s Caster Wheels," IEEE Trans. on Control Systems Tech., vol. 19, pp. 1317-1326, 2011 |
| [9] | R. C. Simpson, "Smart Wheelchairs: A Literature Review," Journal of Reh. Research & Dev., vol. 42, pp. 423–436, 2005 |
| [10] | R. C. Simpson, D. Poirot, and F. Baxter, "The Hephaestus Smart Wheelchair system," IEEE Trans. on Neural Systems and Rehabilitation Engineering, vol. 10, pp. 118 - 122, 2002 |
| [11] | S. P. Levine, D. A. Bell, L. A. Jaros, R. C. Simpson, Y. Koren, and J. Borenstein, "The NavChair Assistive Wheelchair Navi- gation System," IEEE Transactions on Rehabilitation Engin- eering, vol. 7, pp. 443 - 451, 1999 |
| [12] | R. Simpson, E. LoPresti, S. Hayashi, I. Nourbakhsh, and D. Miller, "The Smart Wheelchair Component System," Journal of Reh. Research & Dev.t, vol. 41, pp. 429–442, 2004 |
| [13] | Q. Zeng, B. Rebsamen, E. Burdet, and C. L. Teo, "A Collaborative Wheelchair System," IEEE Trans. on Neural Systems and Rehabilitation Eng., vol. 16, pp. 161 - 170, 2008 |
| [14] | D. An and H. Wang, "VPH: A New Laser Radar Based Obstacles Avoidance Method for Intelligent Mobile Robots," in Proceedinfs of the 5th Congress on Intelligent Control and Automation, 2004, pp. 4681-4685 |
| [15] | J. Borenstein and Y. Koren, "The Vector Field Histogram-Fast Obstacle Avoidance for Mobile Robots," IEEE Tran. on Robotics and Auto., vol. 7, pp. 278-288, 1991 |
| [16] | I. Ulrich and J. Borenstein, "VFH+: Reliable Obstacle Avoidance for Fast Mobile Robots," in Proceedings of the IEEE Inter. Conf. on Robots and Auto., 1998, pp. 1572-1577 |
| [17] | Z. Xiang, Z. Xu, and J. Liu, "Small obstacle detection for autonomous land vehicle under semi-structural environme- nts," in Proceedings of IEEE Intelligent Transpor- tation Systems, 2003, pp. 293 - 298 |
| [18] | S. P. Parikh, V. G. Jr., V. Kumar, and J. O. Jr., "Usability Study of a Control Framework for an Intelligent Wheelchair," in Proceedings of the IEEE International Conference on Robotics and Automation, 2005, pp. 4745-4750 |
| [19] | Y. Murakami, Y. Kuno, N. Shimada, and Y. Shirai, "Intelligent Wheelchair Moving among People Based on Their Observations," in Systems, Man, and Cybernetics, The IEEE International Conference on Systems, Man, and Cybernetics. vol. 2, 2000, pp. 1466-1471 |
| [20] | J. Borenstein and Y. Koren, "Error Eliminating Rapid Ultrasonic Firing for Mobile Robot Obstacle Avoidance," IEEE Trans. on Robotics and Aut., vol. 11, pp. 132-138, 1995 |
| [21] | S. Shoval, J. Borenstein, and Y. Koren, "The Navbelt—A Computerized Travel Aid for the Blind Based on Mobile Robotics Technology," IEEE Transactions on Biomedical Engineering, vol. 45, pp. 1376-1386, 1998 |
| [22] | I. Ulrich and J. Borenstein, "The GuideCane—Applying Mobile Robot Technologies to Assist the Visually Impaired," IEEE Transactions on Systems, Man, and Cybernetics-Part A: System and Humans, vol. 31, pp. 131-136, 2001 |
| [23] | Y. L. Ip, A. B. Rad, and Y. K. Wong, "Autonomous Exploration and Mapping in an Unknown Environment," in Proceedings of The International Conference on Machine Learning and Cybernetics, 2004, pp. 4194 - 4199 |
| [24] | P. Cerri and P. Grisleri, "Free Space Detection on Highways using Time Correlation between Stabilized Sub-pixel precision IPM Images," in Proceedings of the IEEE Inter. Conf. on Robotics and Automation, 2005, pp. 2223-2228 |
| [25] | H. Sermeno-Villalta and J. Spletzer, "Vision-based Control of a Smart Wheelchair for the Automated Transport and Retrieval System (ATRS)," in Proceedings of the IEEE Inter. Conf. on Robotics and Automation, 2006, pp. 3423 - 3428 |
| [26] | C. J. Taylor and D. J. Kriegman, "Vsion-Based Motion Planning and Exploration Algorithm for Mobile Robots," IEEE Trans. on Robots and Auto., vol. 14, pp. 417-426, 1998 |
| [27] | P. E. Trahanias, M. I. A. Lourakis, A. A. Argyros, and S. C. Orphanoudakis, "Vision-Based Assistive Navigation for Robotic Wheelchair Platformsy," in Machine Vision Applica- tions Workshop, Graz, Austria, 1996 |
| [28] | Y. W. Huang, S. Y. Chien, B. Y. Hsieh, and L. G. Chen, "Global Elimination Algorithm and Architecture Design for Fast Block Matching Motion Estimation," IEEE Trans. on Circuits and Sys. For Video Tech., vol. 14, pp. 898-907, 2004 |
| [29] | J. Vanne, E. Aho, T. D. Hämäläinen, and K. Kuusilinna, "A High-Performance Sum of Absolute Difference Implemen- tation for Motion Estimation," IEEE Trans. on Circuits and Sys. for Video Tec., vol. 16, pp. 876-883, 2006 |
| [30] | K. Lengwehasatit and A. Ortega, "Probabilistic Partial- Distance Fast Matching Algorithms for Motion Estimation," IEEE Transactions on Circuits for Video Technology, vol. 11, pp. 139-152, 2001 |
| [31] | M. Z. Brown, D. Burschka, and G. D. Hager, "Advances in computational stereo," IEEE Transactions on Pattern Analysis and Machine Intel., vol. 25, pp. 993 - 1008, 2003 |
| [32] | H. F. Ates and Y. Altunbasak, "SAD Reuse in Hierarchical Motion Estimation For The H.264 Encoder," in Proceedings of the IEEE inter. on Acoustic, Speech, and Signal proc. 2005 |
| [33] | D. L. Fowler, T. Hu, T. Nadkarni, P. K. Allen, and N. J. Hogle, "Initial trial of a stereoscopic, insertable, remotely controlled camera for minimal access surgery," Surg Endosc, vol. 24, pp. 9–15, 2010 |
| [34] | S. Rodríguez, J. F. D. Paz, P. Sánchez, and J. M. Corchado, "Context-Aware Agents for People Detection and Stereo- scopic Analysis," Trends in PAAMS, AISC vol. 71, pp. 173–181, 2010 |
| [35] | S. Rodríguez, F. d. l. Prieta, D. I. Tapia, and J. M. Corchado, "Agents and Computer Vision for Processing Stereoscopic Images," HAIS pp. 93–100, 2010 |
| [36] | R. A. Hamzah, R. A. Rahim, and Z. M. Noh, "Sum of Absolute Differences Algorithm in Stereo Correspondence Problem for Stereo Matching in Computer Vision Application " in The 2010 IEEE Conference, 2010, pp. 652-656 |
| [37] | M. Brezan, "HYBRID METHOD OF 3-D IMAGE RECONSTRUCTION FROM STEREO PICTURES," in The 2008 IEEE 3DTV-Conference, 2008, pp. 189-192 |
| [38] | S. Gutiérrez and J. L. Marroquín, "Robust approach for disparity estimation in stereo vision," Image and Vision Computing, vol. 22, pp. 183-195, 2004 |
| [39] | E. Izquierdo, "Disparity/segmentation analysis: matching with an adaptive window and depth-driven segmentation," IEEE Transactions on Circuits and Systems for Video Technology, vol. 9, pp. 589 - 607, 1999 |
| [40] | T. H. Nguyen, J. S. Nguyen, D. M. Pham, and H. T. Nguyen, "Real-Time Obstacle Detection for an Autonomous Wheelchair Using Stereoscopic Cameras," in The 29th Annual Inter. Conf. of the EMBC, 2007, pp. 4775 - 4778 |
| [41] | S. Thrun, W. Burgard, and D. Fox, Probabilistic Robotics: Cambridge, Mass. : MIT Press, 2005 |
| [42] | Y. L. IP, A. B. Rad, and Y. K. Wong, "Autonomous Exploration and Mapping in An Unkown Environment," in Proceedings of the IEEE Third International Conference on Machine Learning and Cybernetics, 2004, pp. 4194-4199 |
| [43] | R. K. Srivastava and K. Deb, "Bayesian Reliability Analysis under Incomplete Information Using Evolutionary Algori- thms," pp. 435–444, 2010 |
| [44] | S. Salti and LuigiDiStefano, "On-Line Learning of the Transition Model for Recursive Bayesian Estimation," in the 2009 IEEE 12th International Conference on Computer Vision Workshops, 2009, pp. 428-435 |
| [45] | R. Singh, E. Manitsas, B. C. Pal, and G. Strbac, "A Recursive Bayesian Approach for Identification of Network Configu- ration Changes in Distribution System State Estimation," IEEE Transactions on Power Systems, vol. 25, pp. 1329-336, 2010 |
| [46] | V. Fox, J. Hightower, L. Liao, D. Schulz, and G. Borriello, "Bayesian Filtering for Location Estimation," IEEE Pervasive Computing, vol. 2, pp. 24-28, 2003 |
| [47] | J. Borenstein and Y. Koren, "The Vector Field Histogram - Fast Obstacle Avoidance For Mobile Robots," IEEE Journal of Robotics and Automation, vol. 7, pp. 278-288, 1991 |
| [48] | J. Borenstein and Y. Koren, "Error Eliminating Rapid Ultrasonic Firing for Mobile Robot Obstacle Avoidance," IEEE Tran. on Robotics and Auto., vol. 1, pp. 132-138, 1995 |
| [49] | I. Ulrich and J. Borenstein, "VFH+: Reliable Obstacle Avoidance for Fast Mobile Robots," in Proceedings of the 1998 IEEE Intcrnational Conference on Robotics & Auto- mation, 1998, pp. 1572-1577 |
| [50] | S.-Y. Cho, A. P. VINOD, and K. W. E. CHENG, "Towards a Brain-Computer Interface Based Control for Next Generation Electric Wheelchairs " in The 2009 3rd International Conf. on Power Electronics Systems and Applications 2009 |
| [51] | Y. Zhang, J. Zhang, and Y. Luo, "A Novel Intelligent Wheelchair Control System Based On Hand Gesture Recognition " in Proceedings of the 2011 IEEEIICME Inter. Conf. on Complex Medical Engineering 2011, pp. 334-339 |
| [52] | C. S. L. Tsui, P. Jia, J. Q. Gan, H. Hu, and K. Yuan, "EMG-based Hands-Free Wheelchair Control with EOG Attention Shift Detection " in Proceedings of the 2007 IEEE Inter., Conf. on Rob. and Biomimetics, 2007, pp. 1266-1271 |
| [53] | L. Wei, H. Hu, T. Lu, and K. Yuan, "Evaluating the Performance of a Face Movement based Wheelchair Control Interface in an Indoor Environment " in Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics, 2010, pp. 387-392 |
| [54] | J. Heitmann, C. Köhn, and D. Stefanov, "Robotic Wheelchair Control Interface based on Headrest Pressure Measurement " in 2011 IEEE Inter. Conf. on Rehabilitation Robotics 2011 |
| [55] | T. H. Nguyen and K. T. Vo, "Freespace Estimation in an Autonomous Wheelchair Using a Stereoscopic Camera System " in The 32nd Annual International Conference of the IEEE EMBS, 2010, pp. 458-461 |
| [56] | D. An and H. Wang, "VPH: A New Laser Radar Based Obstacle Avoidance Method for Intelligent Mobile Robots," in Proceedings of the 5th World Congress on Intelligent Control and Automation, 2004, pp. 4681-4685 |
| [57] | C. Urdiales, B. Fernandez-Espejo, R. Annicchiaricco, F. Sandoval, and C. Caltagirone, "Biometrically Modulated Collaborative Control for an Assistive Wheelchair," IEEE Transactions on Neural Systems And Rehabilitation Engineering, vol. 18, pp. 398-408, 2010 |
| [58] | H. T. Trieu, H. T. Nguyen, and K. Willey, "Shared Control Strategies for Obstacle Avoidance Tasks in an Intelligent Wheelchair," in The 30th Annual International IEEE EMBS Conference, 2008, pp. 4254-4257 |




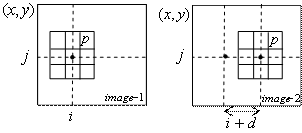
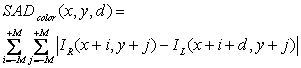
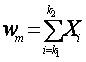
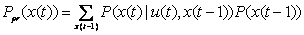
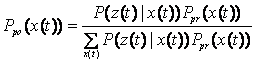
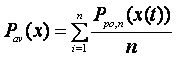


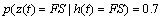
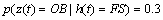
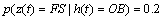
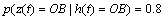
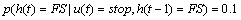
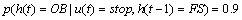
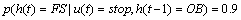
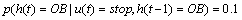
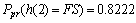
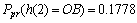
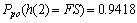
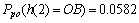

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML