1. Introduction

The kVp control of the X-ray device is a measure for the energy level of the emitted X-rays and corresponds to the penetrating power of the beam. To increase the contrast on the radiographic image, the kVp should be adjusted according to the type of the tissue. The kVp affects not only the intensity reaching the image receptor but also the subject contrast of the image. An uncalibrated X-ray machine leads to unnecessary exposure of the patients. For this reason, the kVp adjusting circuit of the X-ray machines should be controlled on regular basis. There are various ways to measure the kVp like direct measuring method (with high-voltage divider), X-ray spectroscopy or the Wisconsin kVp test cassettes.

Electronic kVp-meters provide a measurement based on the change in X-ray transmission through varying thicknesses of filtration. kVp-meters in general do not measure the true peak voltage; but rather an effective kV value by integrating the detector's outputs over exposure time and then taking their ratio. The instrument then corrects this value, usually according to a switch set by the user to indicate what type of X-ray machine (1Φ or 3Φ or DC) is being measured, to give an effective kVp by knowing the amount of ripple in the waveform.

The method employed in this article relays on the same principle, namely the dependence of the linear attenuation coefficient µ of copper on the energy level of the X-ray photons: if µ can be measured, then the energy level of the photons, hence the kVp can be determined. Copper material is used since its µ exhibits a smooth behaviour within the energy range of X-ray imaging[1,2] as can be seen from Figure 1.

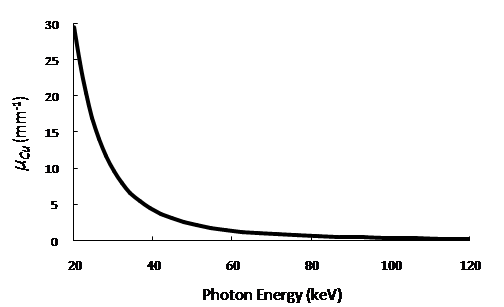Figure 1. The relation between the linear attenuation coefficient of copper and the incident photon energy.

However this behaviour is valid only for monochromatic X-ray beam. In practice, the energy spectrum generated at a certain kVp exhibits a continuous behaviour calledBrehmsstrahlung continuum up to the largest possible keV level which is in fact the kVp, with a few peaks called characteristic X-rays. Filtration eliminates the relatively lower energy photons and the effective peak level is shifted to the right, where the overall intensity, namely the number of photons decreases. Therefore it is important to have a µ-kVp relationship rather than µ-photon energy.

2. Method and Measurement

A. Calculation of µ

The relationship between the intensities of an X-ray beam, before and after passing through a material of thickness t is formulated by the Beer- Lambert Law, where µ is the effective linear attenuation coefficient of the material and corresponds to the mean energy level of the photons[3,4]:

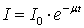Copper is used as filtering material. The thickness and radiation intensity are known. But the intial intensity of the beam I₀ is also not known like µ_Cu. Since there are two unknowns, two equations are needed to solve and. two copper slabs of thicknesses of 0.5mm and 1mm respectively were irradiated from an X-ray source (Siemens Multix Compact K with Half Value Layer = 3mm Al). Then the intensities of the beams are given as

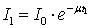and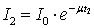

By taking the ratio of X-ray dose measurements I₁ and I₂ for the two slabs of thicknesses t₁ and t₂, the common term I₀ was eliminated and the equation readily solved for µ_Cu:

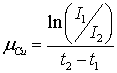(1)

X-ray doses, which are proportional to the intensities, were measured using the Radcal 2026C dosimeter. The X-ray unit exposure was varied between 20-40mAs at the kVp range (60 to 120kVp) of the measurements, with a source to object distance of 80cm. The calibration accuracy of the X-ray source was verified against a Victoreen 07-743kVp-meter.

Using the above formula, the effective linear attenuation coefficient of copper is plotted as a function of the applied tube kVp as shown in Figure 2:

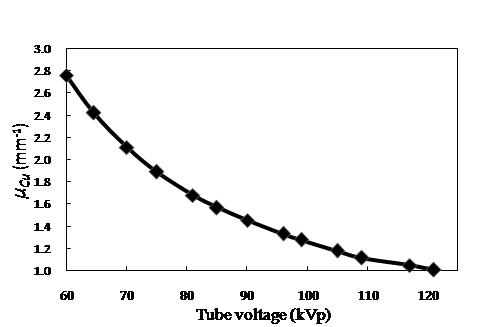Figure 2. The relation between linear attenuation coefficient and kVp.

µ_Cu varies between 2.8mm^-1 and 1mm^-1 in the range 60-120kVp. This relationship is then stored as a look-up table in the memory of the microcontroller to find the corresponding kVp value for the measured µ.

B. System

The block diagram of the kVp meter is shown in Figure 3. When exposed to X-ray, the third photodetector triggers the counter and measurements start.

The X-ray photons incident to the photodiodes are filtered by two different thicknesses Cu filters and hence different currents are generated. These currents are fed into the log-ratio amplifier (LOG101, Texas Instruments) whose output is proportional to the logarithm of their ratio. So, the equation is almost solved. This result only needs to be divided by t₂-t₁ to find µ_Cu.

The microcontroller (ATmega16, Atmel) is the leading component of the circuit. It is chosen due to its ease of programming and internal, fast and accurate 10-bit ADC, which digitizes the output from the log-ratio amplifier. The maximum sampling frequency for 10-bit resolution is 15.4kS/s.

The microcontroller becomes active as the power is switched on. At the start it initializes itself and waits for the trigger signal. As soon as the trigger switches to HIGH, the microcontroller starts the ADC to sample the voltage from the log-ratio amplifier and starts also the 16-bit internal counter to measure the exposure time.

During exposure, the trigger signal is always HIGH; the ADC repetitively samples the output of the log-ratio amplifier of which the average value is calculated at every eighth sample and stored in the RAM. So, the actual frequency of the samples is reduced to 1.9kS/s. Sampling is performed over the exposure time in a continuous manner. Since the frequency of the single phase or three phase units are 50-60Hz, this sampling frequency allows the ADC one cycle to sample with 32 points and the peaks will not be missed. So, it is independent of the X-ray waveform. After the exposure is over, the measured data are processed by the microcontroller. The minimum value of this array corresponds to the highest value of the tube voltage during the whole exposure period, namely the kVp, which is calculated using the previously stored look-up table and displayed. The microcontroller can distinguish between exposure start-end and cyclic voltage rise in the case of single and 3 phase X-ray units.

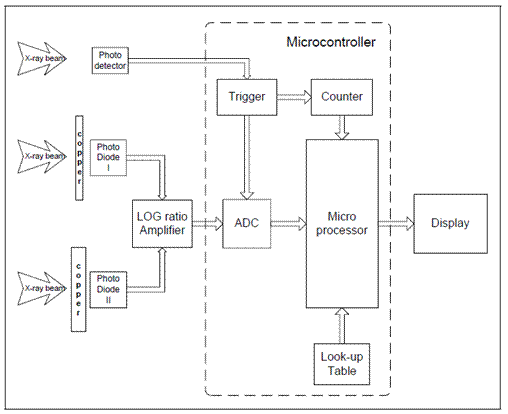Figure 3. Block diagram of the kVp meter.

Like the ADC, the 16-bit counter is also triggered at the start of the exposure. It keeps counting till the end of exposure. Exposure times larger than 5 seconds cannot be measured since an overflow occurs. The look-up table contains the reference values for the measurements. For each measurement, the microcontroller finds the corresponding kVp value between the reference values.

C. Logarithm Operation

The ratio I₁/I₂ is already informative on the kVp level since logarithm and division are reversible operations. Most of the previous designs used this ratio and a look-up table to find the corresponding kVp. The graph of this ratio vs. kVp exhibits a more curved behaviour which may result in congested values in the look-up table for the higher kVp levels. Logarithmic operation on the other hand, makes the graph more linear, thus increases the precision especially at higher kVp levels (Figure 5).

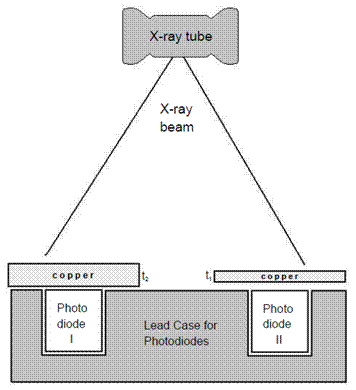Figure 4. Placement of the photodetectors inside a lead case to allow only beams from the X-ray source to reach the photodiodes.

Figure 5. Ratios of intensities and logarithm of ratios vs. kVp.

3. Results and Discussion

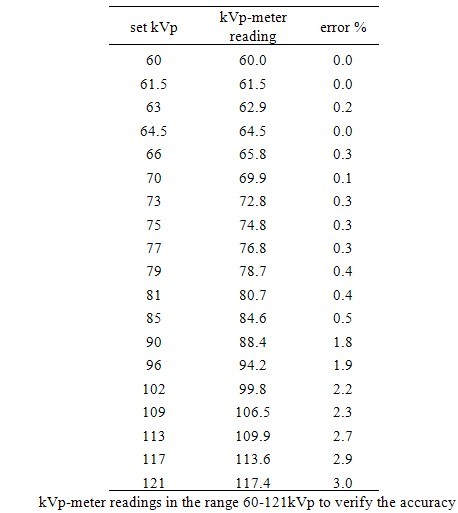
A. Accuracy

Following further correction of the look-up table, the device performed with a better accuracy. Siemens Multix Compact K was used to evaluate the accuracy of the kVp meter. Results are given in Table 1. The accuracy of the prototype unit was less than or equal 0.4% for kVp values between 60 and 81; and for kVp measurements above 90 kVp the error reached 3% at 121kVp as shown in Table 1.

B. Precision

The kVp on the X-ray unit was set to 81kVp for assessing the precision with repeated measurements. The mean value and the coefficient of variation, defined as the ratio of the standard deviation to the mean value, were calculated as 80.72kVp and 0.08% respectively, which is below the 1% limit.

C. Dependence on mAs

To test the dependency of the measurements on the exposure level, several measurements were conducted at constant kVp, but varying mAs (5 to 60mAs). There were no deviations in the readings. It is concluded that the device measurements are independent of mAs settings on the X-ray unit over a wide range of mAs.

Table 1. Accuracy of the KVP-Meter

D. Dependence on positioning

To test the dependency of the accuracy on positioning, the alignment of the device with the central beam was off by 7cm maximum in any direction. There were no deviations that can be reported.

E. Conclusion

An accurate, cheap and reliable kVp meter with an exposure timer is built. For ease of use, the device can be calibrated at 50cm or 40cm tube distances. Continuous sampling over the exposure time also made the measurements independent of the X-ray waveform.