1. Introduction

This manuscript reveals details conceived by Chinese scholars (Wu Zhong, Zhu Ting, and Wei Kongming) to defeat missile defense systems by employing manoeuvring warheads as presented at the twenty-ninth Chinese control conference in Beijing. The technology presented is the native expertise of Sands, while Lu, Chu, and Cheng are language experts specializing in Chinese and English.

With the development of mobile, manoeuvrable missile technology, ballistic missile reentry warheads equipped has become the inevitable demand of modern warfare. Reentry warheads with the ability to penetrate air defences while maneuvering can not only improve accuracy, but also implement maneuvering avoiding and improve viability when facing highly-developed missile defense technology.

Warhead reentry attitude control is one of the core and key technologies that needs to solve in order to improve manoeuvrability of the warhead. At present, most ballistic missiles generally adopt the schemes of the aerodynamic rudder control, thrust vector control, and moving centroid control when need to control the attitude of the reentry warhead.

The control fin is comparatively more mature technology in engineering, and has been successfully applied in American "Pershing-II" and other missiles. However, when the reentry warhead flights in the dense atmosphere with hypersonic speed, the temperature of the warhead sharply rises, the control fin and its connections with missile body will face a serious erosion problem, and thus greatly challenge the materials of the control fin. Meanwhile, the calibre of the reentry warhead (and necessarily the outer shell of the nosecone) is on-average much larger than that of the missile, and less efficient control fin restricts the maximum angle of attack that will not be able to meet the requirements of large maneuvers.

Although the side-jet engine that adopted vectored thruster does not have the above problems, the control-force generated and work-time is restricted by the fuel that the missile carried. At the same time, fuel consumption can cause the drift of missile centroid, and the side-jet interaction with the incoming flow will cause some disturbance force and torque, and thus affect the attitude control of the reentry warhead.

The attitude control by changing centroid, on the other hand, relies on the movement of the moving mass to change the turning inertia and the centroid of the warheads, and thus to achieve a slight attitude maneuver of the warhead. Since the moving mass is mounted inside the warhead directly, it does not affect the aerodynamic shape of the warhead, and there is no rudder erosion problem. Its structure is simple and has been applied in Russia "Topol-M" and other missiles. However, the quality slider movement alone cannot make a larger warhead attitude maneuver; moreover, and the design of attitude controller is relatively complicated.

To avoid the problems in the above control programs, the National University of Defense Technology proposed a warhead attitude control program based on the momentum wheel. Similar to centroid control, the momentum wheel is mounted directly inside of the warhead, eliminating the rudder erosion problem. It also allows warheads to maintain a good aerodynamic shape. However, the torque that the momentum wheel can provide is relatively small, that is not enough to achieve a larger warhead maneuver control.

In contrast, a single-gimbaled control moment gyroscope (SGCMG) applies smaller framework movement yet output larger control torque. It is efficient, with good dynamic feature, and more suitable for attitude stability and control of highly maneuvering reentry warheads. However, China has not conducted research on how to use SGCMGs to control attitude motion of reentry warheads. In the international arena, the research in this field is only in the conceptual study phase.

Therefore, in order to improve the ability of the mobile penetration of the reentry warhead, this paper will use SGCMG as the internal actuator to design the attitude control system of the reentry warhead, so to achieve the attitude stability and attitude maneuver of highly maneuvering reentry warheads. Remainder of this paper is organized as: the second part establishes the attitude dynamics model of the reentry warhead based on SGCMG; the third part designs the attitude controller and SGCMG steering law to for the attitude control system of the reentry warhead based on SGCMG; the fourth part takes a simulation verification to SGCMG based attitude control system of the reentry warhead, using a certain type of reentry warheads as an example; the last part is the conclusion of this paper.

2. Model of Attitude Dynamics

To provide convenience for study, it is assumed the warhead is neutrally static stable [5, 6]. A total of n SGCMGs were placed within the warhead for attitude control. According to the momentum-exchange principle, these SGCMG produce internal moments for the control of the attitude of warhead.

2.1. The SGCMG Model

For a SGCMG system that consists of n numbers of SGCMG, let the gimbal angles be σ=[σ₁, …, σ_n]^T, angular momentum be h=[h₁, h₂, h₃]^T, thus[7, 8]:

(1)

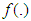where represents the nonlinear kinematic relation of the SGCMG system, while the symbol 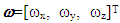represents the angular velocity of warhead coordinate system relative to the earth-centered equatorial inertial coordinated system. The time-variant angular momentum of the SGCMG system is referred to as the resulting moment, u, of the warhead coordinate system, and it can be expressed as the following:

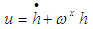(2)

where .

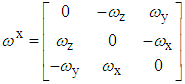According to Eq. (1), we have:

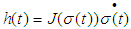(3)

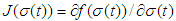where , is a Jacobi matrix.

2.2. The Attitude Kinematics

Let the attitudes of warhead coordinate system relative to the earth-centered equatorial inertial coordinated system be described as 3-1-2 Euler angles; and the symbols 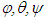denote the roll angle, pitch angle and yaw angle, respectfully. Assuming that 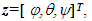the relation of attitude kinematics can be expressed as

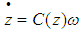(4)

Where .

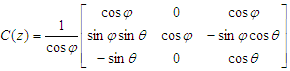2.3. The Attitude Dynamics

Let the symbol M_q represents the control moment, and I the moment of inertia of the reentry warhead. When the reentry warhead is treated as a solid body, its dynamic equations is

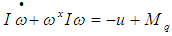(5)

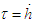According to Eq. (2), we also assumed , thus the Eq. (5) can be rewritten as:

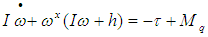(6)

Both of the Eq. (4) and Eq. (6) form the set for the attitude dynamic equations of the warhead.

3. Controller Design

Figure 1 shows that there are two steps for the designs of attitude control system of the SGCMG reentry warhead: the first step is the design of attitude control system, i.e., to provide the commands of required amount of control moment according to the attitude errors, and the second one is the design of formula for SGCMG system control, and the modularization of the control moment commands into each of SGCMG gimbal-angular-velocity command.

Figure 1. Topology of a SGCMG reentry warhead attitude control system

3.1. The Design of Attitude Controller

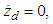
Let the expected attitude z_d be a constant, 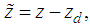using Lyapunov-candidate function as

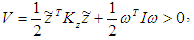(7)

where the symbol K_z represents the symmetric positive-define constant matrix. Taking the time derivatives on both sides of the Eq. (7) and using the Eq. (4) and Eq. (6) into it, one obtains

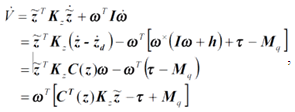(8)

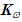since the knowledge of pneumatic moment M_q is not certain, we don’t consider its influence during the design process of attitude controller. If the symbol represents symmetric positive-define constant matrix, let

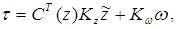(9)

Thus the Eq. (8) can be written as

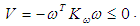(10)

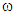According to Lyapunov stability theory and LaSalle invariance principle, one can proof that attitude errors and angular velocity are converge toward zero, while the time reaches to infinite, 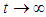, the tracking of expected state could be achieved.

It is noted that in deriving the Eq. (9), the expected attitude 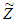was assumed to be a constant (time invariant), while undisturbed moments and other non-modeled factors were not considered. In practice, the expected attitude changes with respect with time, implying the presence of disturbed moments and non-modeled dynamic factors. Those approximations certainly may cause errors in the tracking of attitude. Taking time integration of the Eq. (9), we have

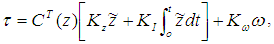(11)

where C^T is a symmetric positive-define constant matrix.

Furthermore, when the Euler angles, representing attitude, are small, the linearization of Eq. (4) with small angles becomes feasible. Thus the Eq. (11) could be simplified as:

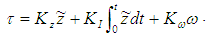(12)

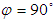However, when the rolling angle equals to 90°, , the Eq. (4) will encounter a computational singularity. When this occurs, other methods are required to describe the attitude, such as quaternions, Rodrigues parameters, etc.

3.2. The Design of Steering Law of SGCMG

For the purpose of producing the control moment that was required for the warhead attitude control, we have to decompose the control moment commands into each SGCMG gimbal angular velocity command, base on the SGCMG steering law. Then, according to the requirements of gimbal angular velocity commands, we control the SGCMG gimbal rotation for the specified amount of control moment, in order to change the warhead attitude. In fact, the SGCMG steering law is a reversed mathematical problem of the SGCMG system kinematic problem, and thus equations (1) and (3) are useful to the design.

In the realm of aerospace navigation and control, the design SGCMG steering law has had many significant achievements [7, 8]. There are various approaches for solving the equations, the current SGCMG steering laws are classified as gimbal angle steering law, gimbal angle velocity steering law, gimbal angle acceleration steering law, etc. There are several forms in the gimbal angle velocity steering law, such as Penrose-Moore pseudo-inverse steering law, zero motion pseudo-inverse steering law, strange robust pseudo-inverse steering law, etc.

For convenience, we adopt the zero motion pseudo-inverse steering law, it has the following form:

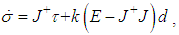(13)

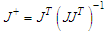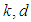Where symbol E is an unit matrix with proper dimension; ; are zero-motion parameters. In general, we choose k>0. If d was set to be the gradient of singular measurement function, we will have gradient-type steering law.

4. Simulation Results and Analysis

To verify the effectiveness of the SGCMGs in the warhead control system, here we mimic Pershing-II reentry warheads, assuming a set of physical parameters for the reentry warhead utilized in simulation studies in the literature [9]. For convenience during the simulation studies, we didn’t consider the influence due to guided links; instead we pay special attention toward the tracking capabilities of expected attitude and the working conditions of control moment gyroscopes due to the warhead attitude control system.

We set that the warhead rolling inertia, and atmospheric disturbance torque of 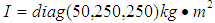. We also adopted the duel parallel structure used in [10], installed 4 SGCMGs in the warhead attitude executive module> The angular momentum of a single SGCMG is 50Nms, while commanded moments are limited to 60Nm, the Eq. (13) was used as the steering law, d represents the gradient of singular measurement function D, 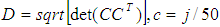. The Eq. (11) was adopted as the attitude steering law. We also adopted the following values:

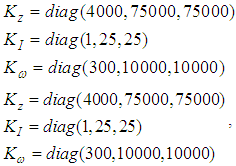The expected attitude was set according to reference [4] as following:

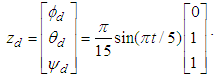(14)

When the initial attitude angles and angular velocities were 0, we used Matlab/Simulink to simulate warhead attitude control systems, and Figs. (2) to (7) show the results of these simulations.

The Figures (2) and (3) show that warhead attitude control system provide high quality tracking of three-axial attitude, under the adopted SGCMG conditions. Once the solutions enter the stable state, the rolling-pass attitude control error is less than 0.1°, and the yawing- and pitching pass attitude control errors are less than 1°. The latter two errors are greater than the former one, this is because that the expected attitude changes according the sine law, so the control moment changes with respect to time, and Figure (4) demonstrates the following point: Since the magnitude of the control moment is limited in 60Nm, the control input moment acting on the warhead, the control became saturated at the beginning period of time integration. Yaw and pitch are bounded within 30 Nm after the solutions became stable, while roll remained in a stable attitude with a control moment always less than 3 Nm.

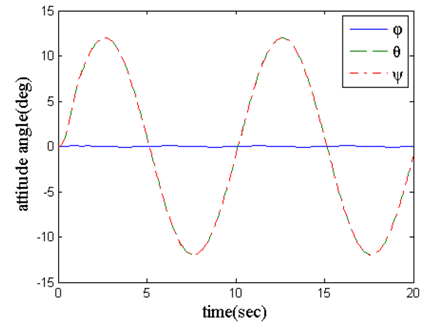Figure 2. Attitude angle tracking curve (attitude angle changes with respect to time)

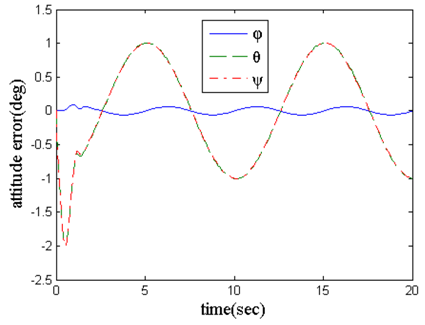Figure 3. Attitude angle tracking error curve (attitude angle error changes with respect to time)

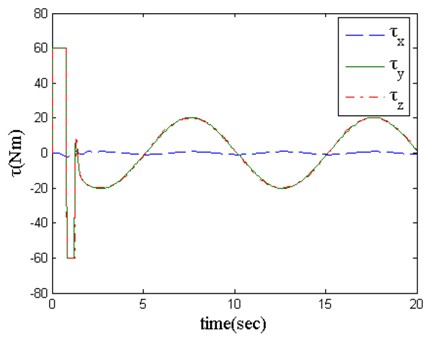Figure 4. Control moment change curve (Control moment changes with respect to time)

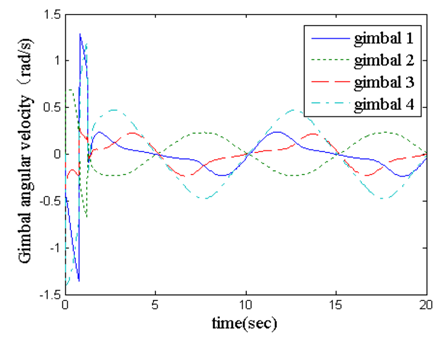Figure 5. The SGCMG gimbal angular speed change curve (changes with respect to time)

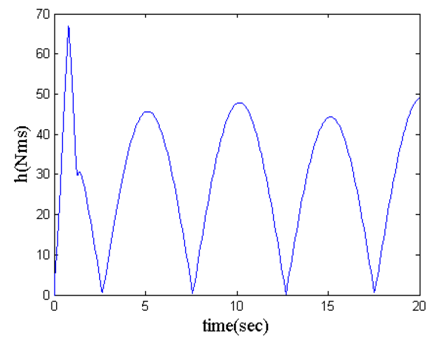Figure 6. The SGCMG system total angular momentum change curve (changes with respect to time)

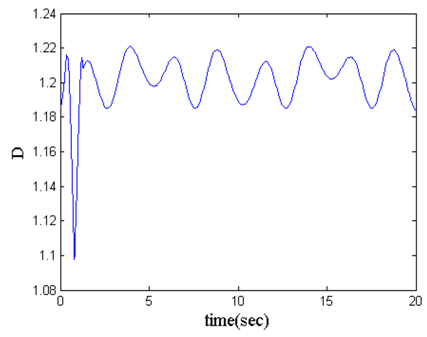Figure 7. The SGCMG system singular measurement change curve (changes with respect to time)

While small angular speeds are required, figure 5 shows the time change of SGCMG gimbal angle speed (less than 1.5rad/s), which is within the range of tolerance of engineering design. The Fig. 6 shows that the peak of total angular momentum of SGCMS system is 70 Nms, which does not reach its saturation value, so unload operation is not required; such situation is feasible in engineering practice. Figure 7 reveals that the measurements of SGCMG singularity have relatively large values from the beginning time to the end, therefore the SGCMG system doesn’t experience any strange phenomena during the entire attitude control processes.

According to the above mentioned analyses of simulation results, we state that the SGCMG could be applied to the attitude control system for reentry warhead, in order to gain warhead attitude stability and control.

5. Conclusions

In this article SGCMGS is used as the attitude controlling actuator under the assumption of indifferently static stability. Based on Lyapunov theory, the warhead attitude controller is designed to gain its attitude movement and stability. Compared with fins and thrusters, the ablation of the actuator can be prevented and the aerodynamic shape can be preserved as SGCMGS are mounted inside the warhead. Compared with the moving mass of flywheels, SGCMGS can output torque large enough to meet the need of movement in terms of large-scope attitude and quick velocity.

However, this article is only a preliminary exploration of the application of SGCMG in the reentry of warhead attitude controlling system regardless of the impact of the guide circuit. Besides, during the warhead’s reentry, the change of the physical index of the model and the saturation of the angular momentum occurring in SGCMG system may also have some impact on the attitude controllability, which needs to be addressed in further research. For example, we can make research on some nonlinear controlling methods with adoptability and robustness, and manipulate the impact of the model’s physical index change on the attitude controllability; or we can make research on applicable means of unloading capability so when the SGCMG system is saturated, the attitude controlling soundly maintains.

5.1. Placing the Research in the Context of the Literature

The U.S. has recently published its latest nuclear posture review [11] in response to a world of rising uncertainty in international security [11, 12], while the U.S. has simultaneously sought to reinvigorate its nuclear enterprise in response [13-14]. Significant research [15-22] has recently renewed interest in the control moment gyroscope’s efficacy for maneuvering free-floating rigid bodies like spacecraft and reentry warheads. Physics-based methods [23-27] have led to innovative techniques [28-30] to autonomously recover from battle damage. These innovative techniques rely on identification of the underlying physics equations [31-37] to provide structure for the choice of control laws. Taken together, these innovations illustrate the effectiveness of modern methods to defeat missile defense and increase the deterrence effect of nuclear weapons amidst a myriad of new applications [38, 39].

ACKNOWLEDGEMENTS

Sections 1 of this manuscript were translated by Danni Lu. Sections 2-4 were translated by Janhwa Chu, while Baolin Cheng translated section 5 and the references. Contextual explanations of the original paper’s research were provided by Sands in addition to the graphics, translation editing and preparation of this manuscript. Sands also wrote the section 4.1 connecting the manuscript to the broader literature.