Soheil Jafari1, Poya Khalaf2, Morteza Montazeri-Gh2
1Department of Aerospace Engineering, Sharif University of Technology, Tehran, Iran
2Department of Mechanical Engineering, Iran University of Science and Technology, Tehran, Iran
Correspondence to: Soheil Jafari, Department of Aerospace Engineering, Sharif University of Technology, Tehran, Iran.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Taking the rapid growth of using multi criteria decision making (MCDM) strategies in multi-objective optimization algorithms into account, this paper presents a multi-objective invasive weed optimization (MOIWO) algorithm based on two posteriori MCDM methods in order to design an optimized controller for aero-engines. For this purpose, the IWO algorithm, as a well-established meta-heuristic optimization algorithm, is firstly extended into a multi-objective version. Then, the problem of controller design for aero-engines is formulated as an engineering optimization problem where a single spool turbojet engine model is used as a case study. Next, in order to select a preferred solution from the Pareto front obtained by the MOIWO algorithm, two posteriori MCDM techniques namely the compromise programming approach (with lp and Tchebycheff Metrics) and the pseudo-weight vector approach have been adopted. Finally, the selected solutions are simulated with the engine model. The analysis of the simulation results shows the effectiveness of the proposed method in design and optimization of the engine controller.
Keywords:
Meta-heuristic optimization algorithms, Multi criteria decision making, Multi-objective optimization, Aero-engine control, Compromise programming approach, Pseudo-weight vector approach
Cite this paper: Soheil Jafari, Poya Khalaf, Morteza Montazeri-Gh, Multi-Objective Meta Heuristic Optimization Algorithm with Multi Criteria Decision Making Strategy for Aero-Engine Controller Design, International Journal of Aerospace Sciences, Vol. 3 No. 1, 2014, pp. 6-17. doi: 10.5923/j.aerospace.20140301.02.
1. Introduction
The optimal, reliable and safe operation of gas turbine engines (GTEs) are the most significant concerns for the designers of these engines. The design of an appropriate control system for the GTE is essential in order to satisfy these concerns and provide satisfactory operation.One of the most widely used control architectures intended to achieve the safe and reliable operation of GTE’s, is the min-max logic arrangement. The min–max approach is used in many GTE control systems such as General Electric’s GE90 and Pratt and Whitney’s PW2000 [1]. The min-max controller is composed of several control loops and is conceived to satisfy the GTE’s different control modes by activating the control loops as needed [2].However, one of the complexities associated with the min-max controller is the design and tuning of its parameters for the optimal operation of the engine.Taking the nonlinear behavior of the engine and the min-max strategy into account, the use of global optimization algorithms is proposed in order to overcome the complexities associated with the design of the min-max controller parameters. For the optimal performance of the GTE, the designed controller should provide satisfactory performance while maintaining reasonable fuel consumption and providing engine durability and operational safety by protecting the engine against its operating limits. Therefore, the problem of tuning the GTE’s controller parameters could be viewed as a constrained multi objective optimization problem.The multi-objective optimization problem admits a set of equally valid alternative solutions which are known as the Pareto-optimal set. These solutions are such that improvement in any objective can only be achieved at the expense of degradation in other objectives, and can only be discriminated on the basis of expert knowledge about the problem. Thus, in a multi-objective optimization procedure, ideally the effort must be made in finding the set of tradeoffs optimal solutions by considering all objectives to be important. After a set of such tradeoffs solutions are found, a user can then use higher-level qualitative considerations to select a final solution from the obtained pareto set [3, 4].This approach to multi objective optimization will help the user gain a much better understanding of the problem and the available alternatives, thus leading to a more conscious and better choice. Furthermore, the resulting multiple Pareto optimal solutions can be analyzed to learn about interdependencies among decision variables, objectives, and constraints [5].In classical multi-objective optimization approaches, the task of finding multiple Pareto-optimal solutions is achieved by executing many independent single-objective optimizations, each time finding a single Pareto-optimal solution [3]. However Evolutionary Multi Objective Optimization (EMO) procedures deal with a population of solutions in every iteration, thus making them intuitive to be applied in multi-objective optimization to find a set of non-dominated solutions [6]. Also in practice, many engineering problems do not have explicit presentation of control variables and/or do not have continuity, which are necessary for applying classical gradient-based optimization techniques [5]. In addition, classical gradient-based optimization techniques need a well-defined starting point which should be significantly close to the final solution in order to reduce the probability of getting trapped in a local optimum [7]. Considering the reasons stated, in this paper, the use of an EMO strategy namely the Multi Objective invasive weed optimization (MOIWO) algorithm has been proposed for the GTE Min-Max fuel controller design problem.The IWO algorithm was proposed by Mehrabian and Lucas in 2006 [8]. This algorithm draws inspiration from the natural behavior and colonization of weeds. In their leading work Mehrabian and Lucas have shown the efficiency of the IWO algorithm compared to other EAs through a set of well-known benchmark problems. In this study, we aim to implement the IWO algorithm as a multi-objective optimization algorithm (MOIWO) and investigate its use in the design and optimization of the GTEs Fuel controller.The organization of this paper is as follows:Section 2 presents the problem description. Section 3 explains the extension of the conventional IWO algorithm into the multi-objective version. The aero-engine controller design process is formulated as an engineering optimization problem in section 4. The results of the MOIWO algorithm are presented in section 5. Section 6 illustrates two posteriori multi-criteria decision making techniques for choosing the preferred solution from the obtained are to front. The optimized results are also simulated in this section in order to confirm the ability of the used techniques in the design and optimization of the aero-engine controller studied in this paper. Finally, section 7 concludes the achievements of the paper.
2. Problem Description
The GTE model and its controller structure are described in this section. The problem variables and objectives are then defined in order to formulate the objective function. The MOIWO method and the optimization results are presented in the next sections.As mentioned earlier, a single spool turbojet engine is used as a case study in this paper. In order to model this engine we have incorporated a block structured model. Block-structure models are widely used to model GTEs for the purpose of controller design. These blocks structured models have fewer parameters as well as shorter run times in comparison with thermodynamic models, and thus are suitable for the integration with optimization algorithms.The Wiener model is one of such block-structure systems which consists of a linear dynamic element in series with a static nonlinear part. The nonlinearity in the Wiener model is caused by the variation of the system static and dynamic characteristics due to the input amplitude. As a result, in this paper, a Wiener model is utilized as an appropriate candidate for the nonlinear gas turbine engine modelling. In general a wiener structure should be constructed between the input and each output of the model. Figure 2 shows the structure the wiener model. Considering the fact that the design of a Min-Max fuel controller for a single spool turbojet engine is studied in this paper, we use a first order transfer function as the dynamic part of the wiener model. The nonlinear static part consists of the steady state values of each output parameter. In this study the nonlinear static part corresponding to each output of the engine’s model is obtained experimentally. In addition the time constants related to the linear dynamic parts of the wiener model is also obtained experimentally. More details about GTE modelling can be found in [9-11]. It is worth noting that in general there are no limitations on the use of wiener block structure models for modelling multi spool engines and the wiener block structure model can be extended for the purpose of modelling such engines.Moreover, an engine control system is designed to satisfy the pilots demand, provide acceptable performance and protect the engine against physical limitations. The Min-Max control algorithm, for the fuel control of the studied GTE in this paper is composed of a steady-state controller part and a transient controller part as shown in Fig.1. More details about the Min-Max control strategy can be found in [2, 12].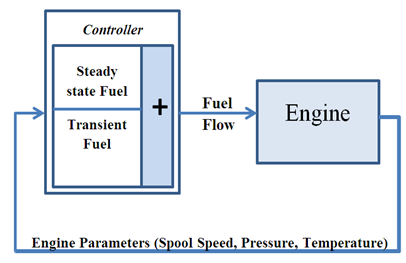 | Figure 1. Engine model and Min-Max fuel controller structure |
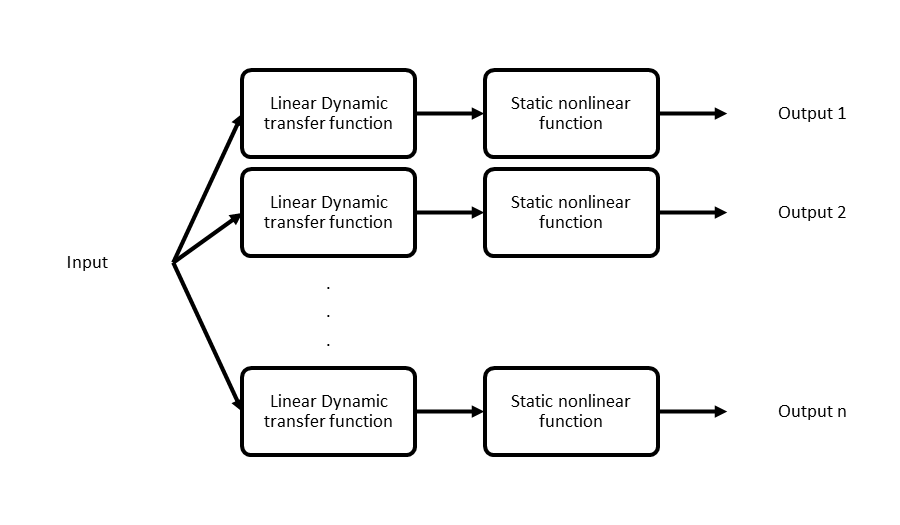 | Figure 2. Weiner model structure |
3. The MOIWO Algorithm
A multi objective (MO) optimization problem differs from a single objective (SO) optimization problem in that in a MO optimization there are multiple conflicting objectives which result in a set of alternative solutions called Pareto optimal solutions, or non-dominated solutions. Thus in a MO optimization problem there are two equally important tasks: an optimization task for finding Pareto optimal solutions and a decision-making task for choosing a single most preferred solution [3]. In regard of finding a set of Pareto optimal solutions, a MO optimization algorithm must peruse two objectives: Finding a set of solutions which lie on the Pareto-optimal front and are diverse enough to represent the entire range of the Pareto front [5]. In order to satisfy these two requirements we incorporate non-dominated sorting and crowding-distance-assignment [6] in the single objective IWO algorithm to formulate the MOIWO algorithm. The MOIWO algorithm starts by initializing a population which is dispread randomly over the d dimensional solution space. After evaluating the fitness of each solution, a dominance ranking scheme is used and each individual is assigned a rank. Note that A solution x(1) is said to dominate another solution x(2), if The solution x(1) is no worse than x(2) in all objectives and the solution x(1) is strictly better than x(2) in at least one objective [5]. Figure 3 illustrates graphically the non-dominated solution set for a bi-objective problem.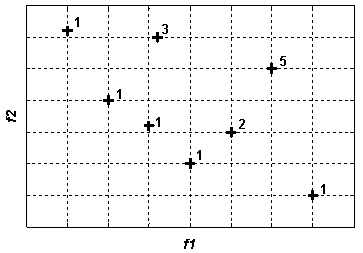 | Figure 3. Non-dominated solution set for an example population in a bi-objective problem |
For the sake of maintaining the diversity of the solutions, the MOIWO algorithm utilizes the crowding distance (CD) assignment. In order to compute the crowding distance for each individual, the population is sorted according to each objective function value. Thereafter the CD corresponding to an objective function is calculated by calculating the absolute normalized difference in the function values of two adjacent solutions and assigning an infinite distance value for the boundary solutions. After calculating the CD for each objective function, the overall CD is calculated as the sum of individual CD values corresponding to each objective [6].Following the calculation of the rank and CD of each individual the weakness (opposite of fitness) of each individual is calculated as specified by the following formula [13]: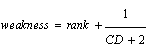 | (2) |
In the next step of the MOIWO algorithm the population is sorted according to its weakness. Sorting the population according to its weakness ensures that no individual with a worse rank can obtain a better fitness value and that the only individuals in the same rank are sorted according to their CD [13].Thereafter each member of the colony produces seeds depending on its own and the colony’s highest and lowest weakness. The number of seeds for each individual is computed linearly with respect to its weakness and the maximum and minimum number of possible seeds by equation (3).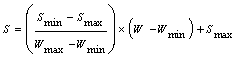 | (3) |
Where S is the number of seeds, 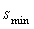 and
and 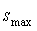 are the maximum and minimum number of seeds respectively, w is the individuals weakness and
are the maximum and minimum number of seeds respectively, w is the individuals weakness and 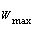 and
and 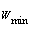 are the maximum and minimum weakness in the population respectively. Figure 4 shows the process of seed reproduction in a colony of weeds.
are the maximum and minimum weakness in the population respectively. Figure 4 shows the process of seed reproduction in a colony of weeds.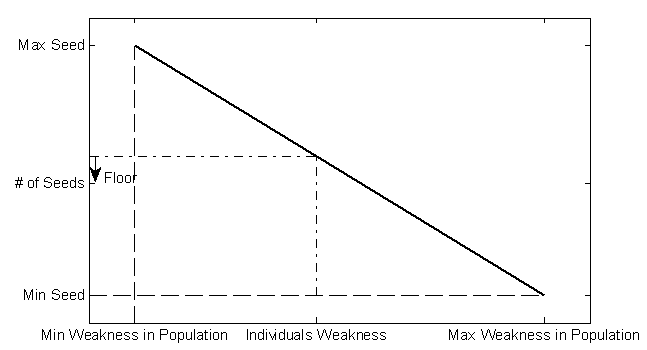 | Figure 4. Seed reproduction process in a colony of weeds |
The generated seeds are then distributed over the solution space by normally distributed random numbers with mean equal to zero, but varying variance. Standard deviation of current iteration is calculated by equation (4). More details about spatial dispersal and its effect to the convergence of the algorithm can be found in [8].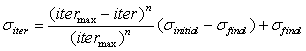 | (4) |
Where 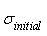 and
and 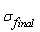 is the initial and final value of standard deviation respectively,
is the initial and final value of standard deviation respectively, 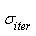 is the current value of standard deviation and
is the current value of standard deviation and 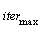 is the maximum number of iterations.Finally when the maximum number of seed is reached, a competitive exclusion mechanism activates to eliminate the seeds with poor fitness. This mechanism works by allowing the weed to produce and disperse seeds. Then the seed and their parents are rank together before weeds with lower fitness are eliminated to reach the maximum allowable population in the colony. Therefore giving a chance of survival to fit offsprings with unfit parents.Also, in order to prevent the loss of good solutions during the optimization process due to random effects an archive elitism approach is incorporated in the MOIWO algorithm [14].The pseudo code for the MOIWO algorithm is summarized as follows:Pseudo code for the MOIWO algorithm1. Initializing a population2. Fitness evaluation3. Assign ranking of each individual4. Assign CD of each individual5. Compute weakness of each individual6. Compute the number of seeds corresponding to each individual weakness7. Distribute the seeds over the search space according to8. Fitness evaluation9. Assign ranking of each individual10. Assign CD of each individual11. If maximum population is reached perform Competitive exclusion12. Updating the Pareto-optimal13. Repeat 5-7 until stopping criterion is fulfilled
is the maximum number of iterations.Finally when the maximum number of seed is reached, a competitive exclusion mechanism activates to eliminate the seeds with poor fitness. This mechanism works by allowing the weed to produce and disperse seeds. Then the seed and their parents are rank together before weeds with lower fitness are eliminated to reach the maximum allowable population in the colony. Therefore giving a chance of survival to fit offsprings with unfit parents.Also, in order to prevent the loss of good solutions during the optimization process due to random effects an archive elitism approach is incorporated in the MOIWO algorithm [14].The pseudo code for the MOIWO algorithm is summarized as follows:Pseudo code for the MOIWO algorithm1. Initializing a population2. Fitness evaluation3. Assign ranking of each individual4. Assign CD of each individual5. Compute weakness of each individual6. Compute the number of seeds corresponding to each individual weakness7. Distribute the seeds over the search space according to8. Fitness evaluation9. Assign ranking of each individual10. Assign CD of each individual11. If maximum population is reached perform Competitive exclusion12. Updating the Pareto-optimal13. Repeat 5-7 until stopping criterion is fulfilled
3.1. Constraint Handling in MOIWO
In this study the constraint handling method described in [15] is integrated into the MOIWO algorithm. In this method the population is firstly divided into feasible and unfeasible solutions. Any feasible solution in the population is preferred to any infeasible solution. Among two feasible solutions, the fitter solution is preferred and infeasible solutions are compared based on only their constraint violation i.e. the solution having a smaller constraint violation is preferred. For the purpose of integrating this constraint handling methodology into the MOIWO algorithm, the weakness of feasible individuals are firstly calculated according to equation (2). In the next step the weakness of unfeasible solution are calculated according to the following equation: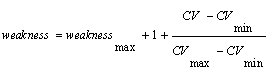 | (5) |
Where weaknessmax is the weakness value of the worst feasible solution in the population, CVmax and CVmin are the maximum and minimum constraint violation of the population and CV is the constraint violation of the individual solution. Thus, the weakness of an infeasible solution not only depends on the amount of its own constraint violation, but also on the population of solutions at hand. Calculating the weakness of unfeasible solutions according to equation (5) ensures that all the feasible solutions in the population are fitter(less weak) than the populations unfeasible solutions.
4. Objective Function Formulation
In this section, optimization of the GTE fuel controller parameters is formulated as a multi-objective optimization problem.For providing an optimum operation of a Gas Turbine Engine, the desired objectives should be optimized simultaneously. These objectives are often conflicting in nature and the optimization of one objective may results in the degradation of other objectives. In the case of a GTE, the manoeuvrability of the engine is attributed to the rise time and settling time of the engines response. Optimizing the engines manoeuvrability results in non-optimal fuel consumption and vice versa. In addition due to the structure of the min max controller, the engine can behave differently in acceleration and deceleration and in consequence the engines performance must be optimized in both acceleration and deceleration. Therefore in this study the engines rise time, settling time and fuel consumption, during an acceleration and deceleration manoeuvre, are selected as objectives. The objective function is formulated as follows: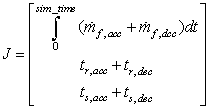 | (6) |
where 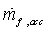 and
and 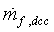 are the instantaneous fuel flow in acceleration and deceleration respectively,
are the instantaneous fuel flow in acceleration and deceleration respectively, 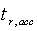 and
and 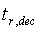 are the rise time and fall time respectively,
are the rise time and fall time respectively, 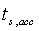 and
and 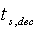 are the settling times in acceleration and deceleration respectively and
are the settling times in acceleration and deceleration respectively and 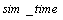 is the simulation time.Moreover, the design variables are the engine controller loop gains. In addition to the objective functions, the engine must also satisfy certain constraints. These constraints include the physical limitations of the engine and constraints placed on the response of the engine during acceleration and deceleration. The constraints are formulated as follow:
is the simulation time.Moreover, the design variables are the engine controller loop gains. In addition to the objective functions, the engine must also satisfy certain constraints. These constraints include the physical limitations of the engine and constraints placed on the response of the engine during acceleration and deceleration. The constraints are formulated as follow: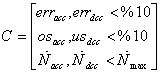 | (7) |
Where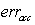 ,
,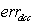 are the steady state error in acceleration and deceleration respectively,
are the steady state error in acceleration and deceleration respectively, 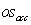 is the over shoot in accelerations,
is the over shoot in accelerations, 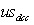 is the undershoot in deceleration and
is the undershoot in deceleration and 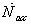 and
and 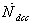 are the acceleration and deceleration respectively.The initial condition of the simulation is the GTE’s idle condition whereas the PLA command applied to the engine in the acceleration and deceleration is shown in Figure 5. As can be seen from this figure the PLA command during acceleration is set to 1.1 times the maximum speed of the engine in order to access the controllers performance in preventing the engine from over speed.
are the acceleration and deceleration respectively.The initial condition of the simulation is the GTE’s idle condition whereas the PLA command applied to the engine in the acceleration and deceleration is shown in Figure 5. As can be seen from this figure the PLA command during acceleration is set to 1.1 times the maximum speed of the engine in order to access the controllers performance in preventing the engine from over speed.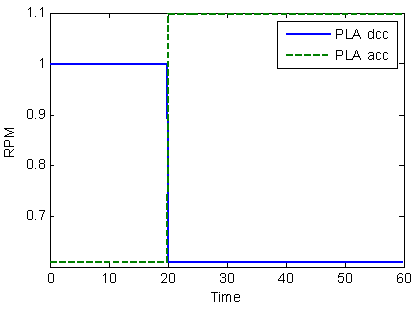 | Figure 5. Applied PLA for simulation |
Ineachiteration of the optimization algorithm, the controller gains are varied and the engine is simulated with the fuel controller in order to find the Pareto-optimal set for the defined problem whilst satisfying the problems constraints.
5. MOIWO Results
The MOIWO algorithm changes the engine’s fuel controller loop gains and simulates the GTE’s performance iteratively until the maximum number of iterations is achieved. In each step, the MOIWO creates a Pareto-set from the solutions with the best rank and the Pareto-set obtained from the previous iteration. Finally, the Pareto-optimal at the last generation is the output of the process. Table 1 shows the parameters used for the MOIWO in this study. It should be noted that the optimization process has been run several times using different parameters in order to prove the convergence of the method. | Table 1. Parameters used in MOIWO |
| | Quantity | Value | | Number of initial population | 100 | | Maximum number of iteration | 100 | | Maximum number of plants | 100 | | Maximum number of seeds | 3 | | Minimum number of seeds | 1 | | Nonlinear modulation index | 3 | | Initial value of standard deviation | 2 | | Final value of standard deviation | 0.01 |
|
|
Figure 6 shows the scatter plot matrix of the Pareto-front obtained by the proposed MOIWO algorithm. The Pareto-front is the image of Pareto-set solution in objective space. From Figure 5 it is observed that the second objective function (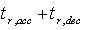 ) is in correlation with the third objective function (
) is in correlation with the third objective function (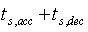 ) because it has been found that minimization of the second objective also minimizes the third objective. The reason for this outcome could be related to the linear part of the wiener structure utilized for the purpose of modeling the single spool turbo jet engine. More precisely, because a first order transfer function is chosen for the linear part of the wiener model ,if the gains of the min max structure are set in a way that switching between the different control loops are performed correctly, minimizing the rise time dose not lead to overshoot and therefore also minimizes the settling time. However considering the overshoot as a constraint is essential for obtaining reasonable optimization results. In addition it is seen from the diagonal graphs of the matrix plot that the pareto optimal solutions are almost spread uniformly on the pareto front and therefore are diverse enough to represent the entire range of the Pareto-optimal front.
) because it has been found that minimization of the second objective also minimizes the third objective. The reason for this outcome could be related to the linear part of the wiener structure utilized for the purpose of modeling the single spool turbo jet engine. More precisely, because a first order transfer function is chosen for the linear part of the wiener model ,if the gains of the min max structure are set in a way that switching between the different control loops are performed correctly, minimizing the rise time dose not lead to overshoot and therefore also minimizes the settling time. However considering the overshoot as a constraint is essential for obtaining reasonable optimization results. In addition it is seen from the diagonal graphs of the matrix plot that the pareto optimal solutions are almost spread uniformly on the pareto front and therefore are diverse enough to represent the entire range of the Pareto-optimal front. 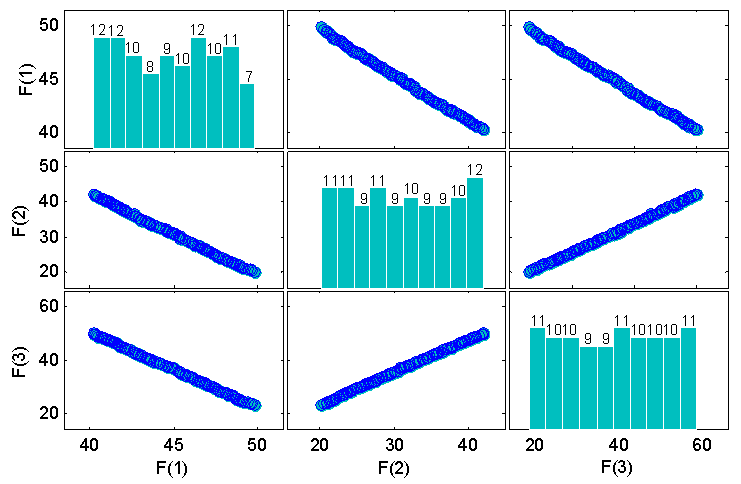 | Figure 6. The scatter plot matrix of the Pareto-front |
The MOIWO algorithm gives a set of non-dominated solution which describes the trade-offs available in the problem. Each point in this set can be used for a specific design strategy with respect to the aim of the designer. In other words, the Pareto-set solution helps the designer to select an appropriate set of the controller gains which satisfy the specific design criterion. Two methods for selecting such a solution are described in the next section.
6. Selection of Preferred Solution
After finding a set of non-dominated and divers set of solutions, the question of selecting a single preferred solution from the non-dominated set for implementation on GTE fuel controller becomes important. Recently various Multi Criteria Decision Making (MCDM) techniques have been used in literature for this purpose [16, 17]. These techniques can be divided into three main categories depending on how the decision-maker (DM) is involved in the optimization process. These three categories are: A priori approach in which the preference information of a DM is incorporated before the optimization, a posteriori approach in which preference information is used after the optimization procedure and an interactive approach in which the DM's preference information is integrated into the optimization algorithm. In this study we have adopted two posteriori MCDM techniques namely the compromise programing approach [18] and the pseudo-weight vector approach [3].In the compromise programing approach a solution is picked which is minimally located from a reference point with respect to a distance measuring metric. Commonly used metrics are: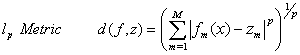 | (8) |
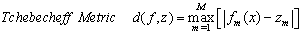 | (9) |
Where M is the number of objectives and z is the reference point. We choose the reference point as the ideal point which is a comprised of the individual best objective function values. Figure 7 shows these metrics for a bi objective optimization problem.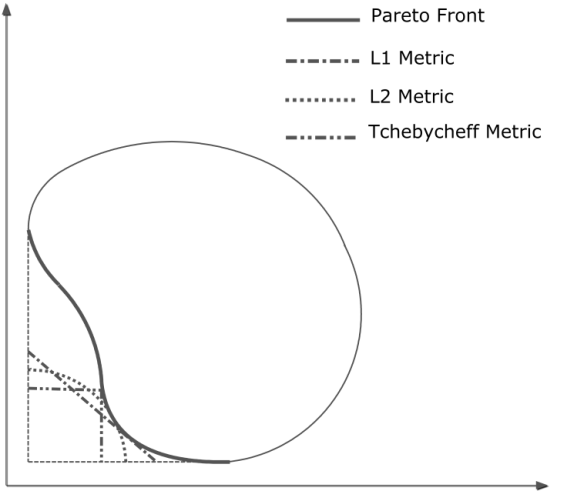 | Figure 7. Different metrics for a bi objective optimization problem |
In the pseudo-weight vector approach a pseudo-weight vector is calculated for each solution. The dimension of the weight vector is equal to the number of objectives. The weight for the ith objective for a minimization problem is calculated according to the following equation: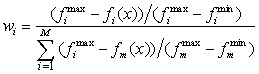 | (11) |
Where 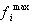 and
and 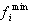 are the maximum and minimum values of each objective function respectively.
are the maximum and minimum values of each objective function respectively. 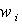 is the relative distance of each solution from its maximum value ineach objective function. Furthermore the sum of all weight components of the weight vector corresponding to a specific solutions, are equal to one. After calculating the weight vector for each solution, the solution which has a weight vector closer to the user- preferred weight vector is chosen.The ideal point and the pareto optimal point for the current problem is shown in Figure 8. The preferred Pareto-optimal solution’s obtained based on the compromise programing approach and using different distance metrics are also shown in this figure. Furthermore, Figure 9 shows the pareto optimal front and the weights of some of the optimal solutions based on the pseudo-weight vector approach. In addition to the solutions picked by the compromise programing approach, three more solutions are picked based on the pseudo-weight vector approach and are shown in table 2. In addition table 2 shows the objective functions, constraint values and the design variables corresponding for each preferred solution.
is the relative distance of each solution from its maximum value ineach objective function. Furthermore the sum of all weight components of the weight vector corresponding to a specific solutions, are equal to one. After calculating the weight vector for each solution, the solution which has a weight vector closer to the user- preferred weight vector is chosen.The ideal point and the pareto optimal point for the current problem is shown in Figure 8. The preferred Pareto-optimal solution’s obtained based on the compromise programing approach and using different distance metrics are also shown in this figure. Furthermore, Figure 9 shows the pareto optimal front and the weights of some of the optimal solutions based on the pseudo-weight vector approach. In addition to the solutions picked by the compromise programing approach, three more solutions are picked based on the pseudo-weight vector approach and are shown in table 2. In addition table 2 shows the objective functions, constraint values and the design variables corresponding for each preferred solution.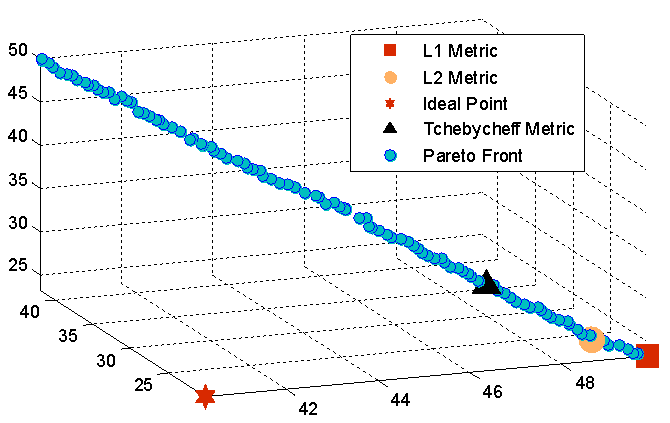 | Figure 8. Pareto optimalfront and choosensoloutions based on the compromise programing approach |
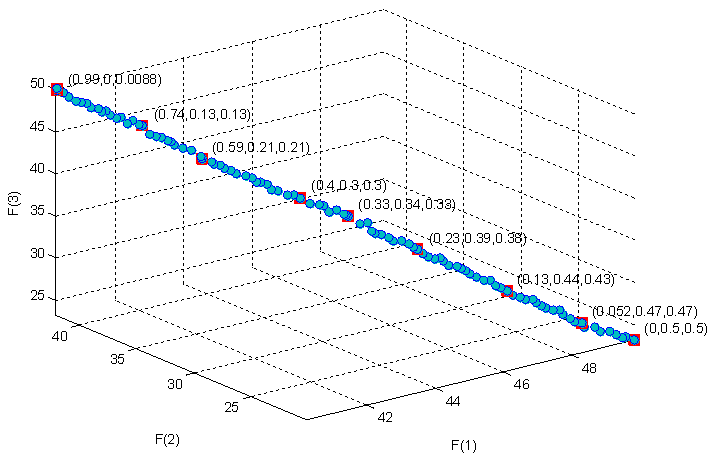 | Figure 9. Pareto optimal front and pseudo weight vectors computed for selected solutions |
Table 2. Objective functions, constraints and design variables for chosen solutions
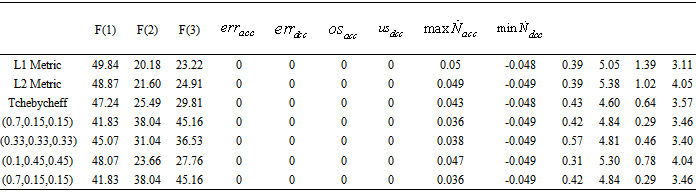 |
| |
|
In order to examine the effectiveness of the proposed approach in optimization of GTE performance, the simulation of engine and controller for the chosen solutions are performed. As seen in table 2 all the preferred solutions have a zero steady state error in both acceleration and deceleration therefore satisfying the steady-state control mode of the GTE. It is also seen from this table that all the preferred solutions have zero over shoot in acceleration and zero under shoot in deceleration which is a very desirable outcome for the GTE controller. Figure 10 shows the PLA tracking of the GTE in acceleration and deceleration. It is observed in Figure 10a that although the PLA is set to 1.1 times the maximum speed of the engine, the GTE controller prevents all the preferred solutions from violating the over speed bound. Figure 11 shows the RPM derivative during acceleration and deceleration of the GTE. It is seen form this figure and table 2 that all the chosen solution have been restricted by the controller to stay within the surge and flameout bounds. These results indicate that all the designed controllers successfully satisfy the physical limitation control mode of the GTE.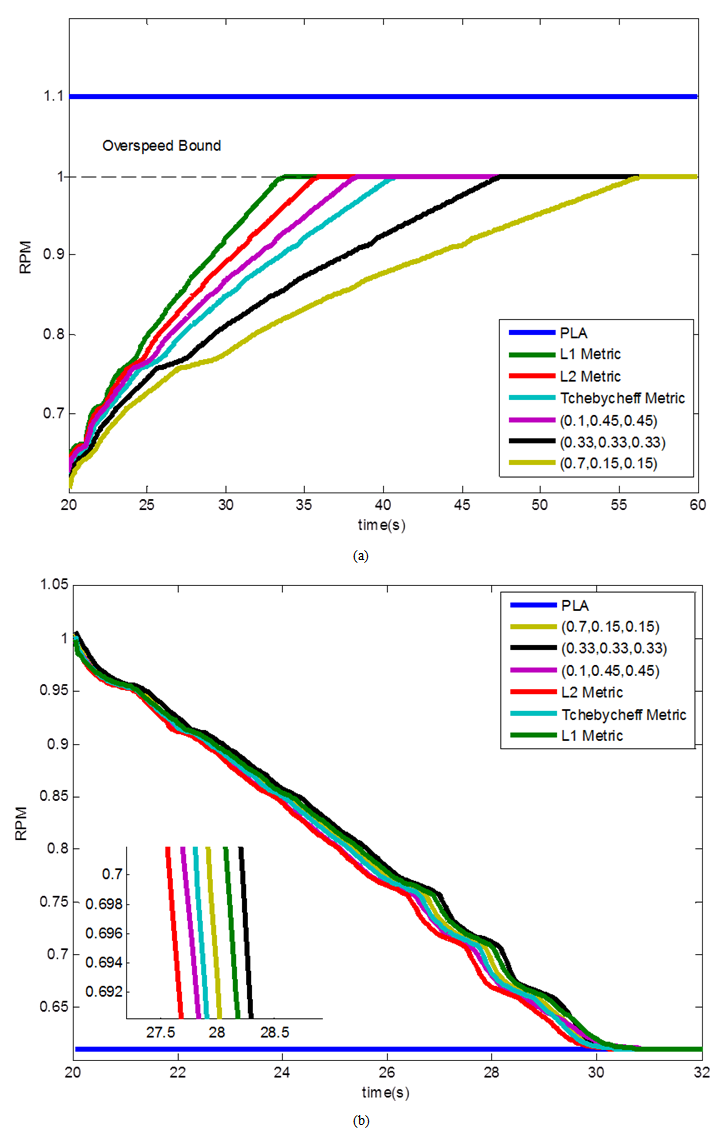 | Figure 10. (a) PLA tracking in acceleration (b) PLA tracking in deceleration |
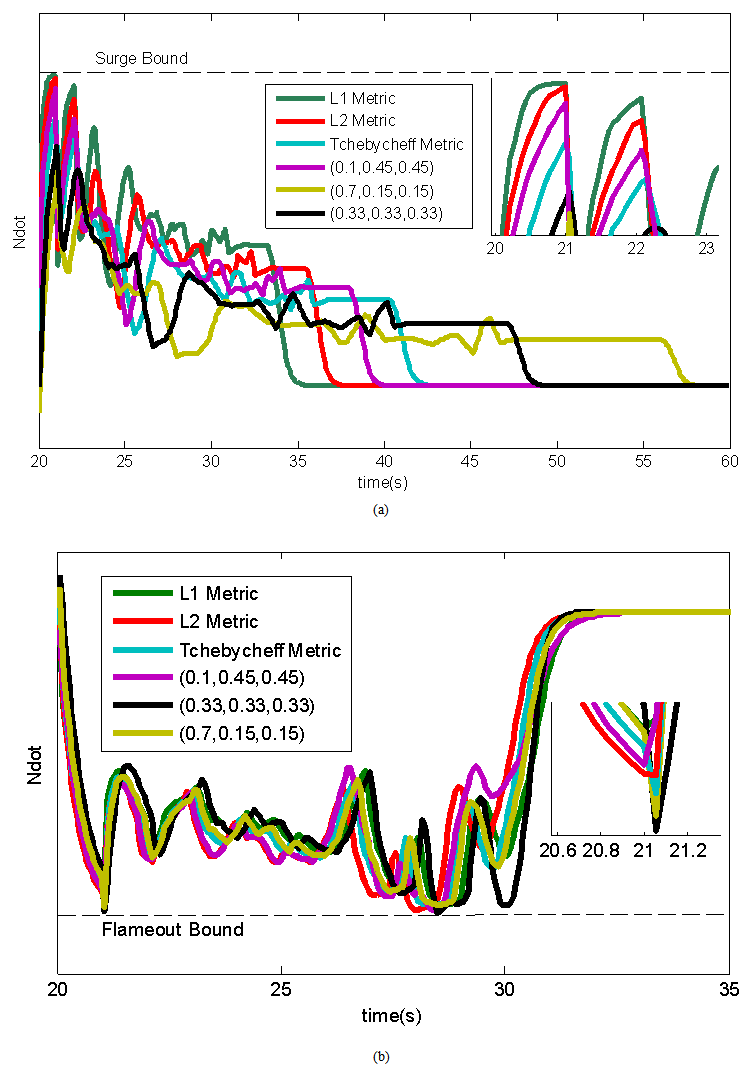 | Figure 11. (a) Ndot in acceleration (b) Ndot in deceleration |
The solution picked by the L1 metric is minimum for the second (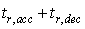 ) and third (
) and third (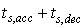 ) objectives however this minimization comes at the price of having a maximum fuel consumption as is seen in figure 12 on the other hand all the other chosen solutions have a better fuel consumption but their response is slower in comparison to the solution chosen by the L1 metric. These results confirm the correlation between rise time and settling time and the trade-off nature between these two objective and fuel consumption. Choosing a large weight for the fuel component of the weight vector in the pseudo-weight vector approach, results in less fuel consumption as is seen in figure 12. On the other hand setting a large weight for the rise time and settling time components of the weight vector results in a faster response with the cost of an increased fuel consumption as seen in figure 12 and figure 10.
) objectives however this minimization comes at the price of having a maximum fuel consumption as is seen in figure 12 on the other hand all the other chosen solutions have a better fuel consumption but their response is slower in comparison to the solution chosen by the L1 metric. These results confirm the correlation between rise time and settling time and the trade-off nature between these two objective and fuel consumption. Choosing a large weight for the fuel component of the weight vector in the pseudo-weight vector approach, results in less fuel consumption as is seen in figure 12. On the other hand setting a large weight for the rise time and settling time components of the weight vector results in a faster response with the cost of an increased fuel consumption as seen in figure 12 and figure 10.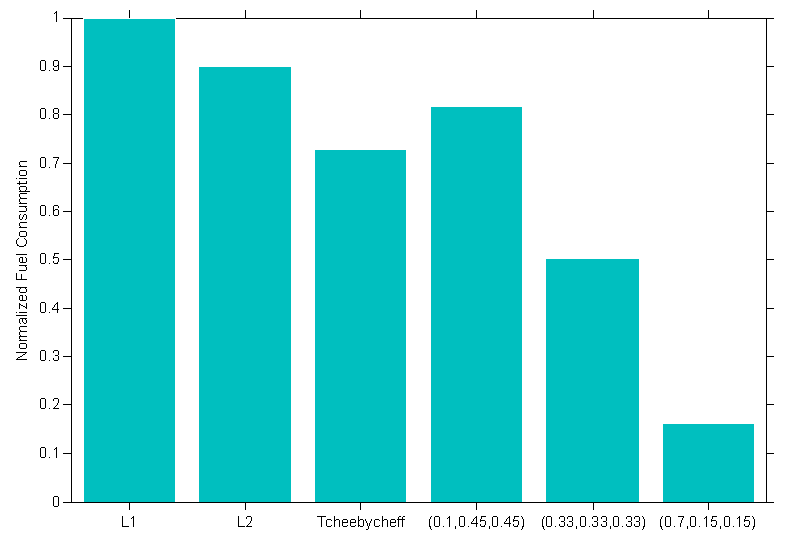 | Figure 12. Normalized Fuel consumption |
In general whenever economic considerations are of higher importance, a larger weight should be set for the fuel consumption component of the weight vector and when manoeuvrability becomes the aim of the design. Solution sets with a larger weight for the rise time and settling time component of the weight vector are good candidates.
7. Conclusions
Two different posteriori multi-criteria decision making techniques are used in this paper to select the preferred solutions from the multi-objective invasive weed optimization pareto front applied to the aero-engine controller design and optimization problem. Thelp and Tchebycheff Metrics are used for the compromise programing approach. The pseudo-weight vector approach is also used in the MCDM process. The results of the paper confirmed the ability of the proposed approach in both development of the MOIWO algorithm and the MCDM approach and the effectiveness of the whole process in the design and optimization of aero-engine controllers. The results obtained from the simulation of the engine and controller illustrate that the optimized controllers successfully satisfy the engine’s control modes without steady state error, overshoot, and undershoot. Also the selected optimized controllers augment the engine with reasonable response time.
References
| [1] | H. Richter, Advanced Control of Turbofan Engines: Springer, 2011. |
| [2] | Morteza Montazeri-Gh, Soheil Jafari, “Evolutionary Optimization for Gain Tuning of Jet Engine Min-Max Fuel Controller,” AIAA Journal of Propulsion and Power, Vol. 27, No. 5, September–October (2011). pp: 1015-1023, DOI: 10.2514/1.B34185 |
| [3] | K. Deb, Multi-Objective Optimization Using Evolutionary Algorithms: An Introduction John Wiley and Sons, 2001. |
| [4] | Morteza Montazeri-Gh, Soheil Jafari, Mohammad R. Ilkhani, “Application of Particle Swarm Optimization in Gas Turbine Engine Fuel Controller Gain Tuning,” Engi-neering Optimization, Vol. 44, No. 2, February (2012), 225–240, http://dx.doi.org/10.1080/0305215X.2011.576760 |
| [5] | J. Branke, K. Deb, and K. Miettinen, Multiobjec-tive Optimization: Interactive and Evolutionary Approaches. Germany: Springer, 2008. |
| [6] | K. Deb, A. Pratap, and S. Agarwal, "A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II," IEEE TRANSACTIONS ON EVOLUTIONARYCOMPUTATION, vol. 6, 2002. |
| [7] | A. Basak, S. Pal, and S. Das, "A modified Invasive Weed Optimization algorithm for time-modulated linear antenna array synthesis," in IEEE Congress on Evolutionary Computation (CEC), Barcelona, 2010, pp. 1-8. |
| [8] | A. R. Mehrabian and C. Lucas, "A novel numer-ical optimization algorithm inspired from weed coloniza-tion," Ecological Informatics, vol. 1, pp. 355– 366, 2006. |
| [9] | C. Evans, "Testing and modeling aircraft gas tur-bines: an introduction and overview," presented at the UKACC International Conference on Control, 1998. |
| [10] | Morteza Montazeri-Gh, Amir Safari, Soheil Jafari, “Optimization of Turbojet Engine Fuel Control System for Safety Consideration,” 7th Iranian Aerospace Society Con-ference 19-21 Feb 2008, Sharif University of Technology, Tehran, Iran |
| [11] | G. G. Kulikov and A. Haydn Thompson, Dynamic Modeling of Gas Turbines. Industrial control center, Glasgow, scotland, U.K, 2003. |
| [12] | Morteza Montazeri-Gh, Mostafa Nasiri, Soheil Jafari , “Real-Time Multi-Rate HIL Simulation Platform for Evalu-ation of a Jet Engine Fuel Controller,” Simulation Modelling Practice and Theory 19 (2011) 996–1006, Elsevier, doi: 10.1016/j.simpat.2010.12.011 |
| [13] | A. H. Nikoofard, H. Hajimirsadeghi, A. Rahi-mi-Kian, and C. Lucas, "Multiobjective invasive weed op-timization: Application to analysis of Pareto improvement models in electricity markets," Applied Soft Computing, vol. 12, pp. 100-112, 2012. |
| [14] | X. Gandibleux, M. Sevaux, K. Sörensen, and V. T’kindt, Metaheuristics for Multiobjective Optimisation vol. 535, 2004. |
| [15] | K. Deb, "An ecient constraint handling method for genetic algorithms," Computer Methods in Applied Me-chanical Engineering, vol. 186, pp. 311-338, 2000. |
| [16] | A. K. Nandi, S. Datta, and K. Deb, "Design of particle- reinforced polyurethane mould materials for soft tooling process using evolutionary multi-objective optimi-zation algorithms," Soft Computing (2012), vol. 16, pp. 989–1008, 2012. |
| [17] | F. Ahmed, A. Jindal, and K. Deb, "Cricket Team Selection Using Evolutionary Multi-Objective Optimization," SEMCCO'11 Proceedings of the Second international conference on Swarm, Evolutionary, and Memetic Compu-ting, vol. 2, pp. 71-78, 2011. |
| [18] | K. Miettinen, Nonlinear multiobjectiveoptimiza-tion. Boston: Kluwer, 1999. |



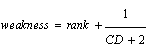
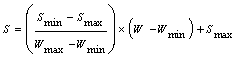
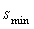 and
and 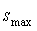 are the maximum and minimum number of seeds respectively, w is the individuals weakness and
are the maximum and minimum number of seeds respectively, w is the individuals weakness and 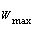 and
and 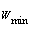 are the maximum and minimum weakness in the population respectively. Figure 4 shows the process of seed reproduction in a colony of weeds.
are the maximum and minimum weakness in the population respectively. Figure 4 shows the process of seed reproduction in a colony of weeds.
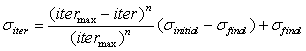
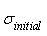 and
and 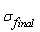 is the initial and final value of standard deviation respectively,
is the initial and final value of standard deviation respectively, 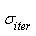 is the current value of standard deviation and
is the current value of standard deviation and 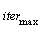 is the maximum number of iterations.Finally when the maximum number of seed is reached, a competitive exclusion mechanism activates to eliminate the seeds with poor fitness. This mechanism works by allowing the weed to produce and disperse seeds. Then the seed and their parents are rank together before weeds with lower fitness are eliminated to reach the maximum allowable population in the colony. Therefore giving a chance of survival to fit offsprings with unfit parents.Also, in order to prevent the loss of good solutions during the optimization process due to random effects an archive elitism approach is incorporated in the MOIWO algorithm [14].The pseudo code for the MOIWO algorithm is summarized as follows:Pseudo code for the MOIWO algorithm1. Initializing a population2. Fitness evaluation3. Assign ranking of each individual4. Assign CD of each individual5. Compute weakness of each individual6. Compute the number of seeds corresponding to each individual weakness7. Distribute the seeds over the search space according to8. Fitness evaluation9. Assign ranking of each individual10. Assign CD of each individual11. If maximum population is reached perform Competitive exclusion12. Updating the Pareto-optimal13. Repeat 5-7 until stopping criterion is fulfilled
is the maximum number of iterations.Finally when the maximum number of seed is reached, a competitive exclusion mechanism activates to eliminate the seeds with poor fitness. This mechanism works by allowing the weed to produce and disperse seeds. Then the seed and their parents are rank together before weeds with lower fitness are eliminated to reach the maximum allowable population in the colony. Therefore giving a chance of survival to fit offsprings with unfit parents.Also, in order to prevent the loss of good solutions during the optimization process due to random effects an archive elitism approach is incorporated in the MOIWO algorithm [14].The pseudo code for the MOIWO algorithm is summarized as follows:Pseudo code for the MOIWO algorithm1. Initializing a population2. Fitness evaluation3. Assign ranking of each individual4. Assign CD of each individual5. Compute weakness of each individual6. Compute the number of seeds corresponding to each individual weakness7. Distribute the seeds over the search space according to8. Fitness evaluation9. Assign ranking of each individual10. Assign CD of each individual11. If maximum population is reached perform Competitive exclusion12. Updating the Pareto-optimal13. Repeat 5-7 until stopping criterion is fulfilled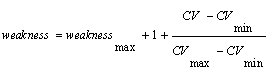
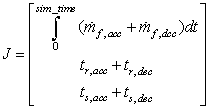
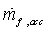 and
and 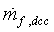 are the instantaneous fuel flow in acceleration and deceleration respectively,
are the instantaneous fuel flow in acceleration and deceleration respectively, 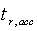 and
and 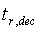 are the rise time and fall time respectively,
are the rise time and fall time respectively, 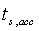 and
and 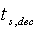 are the settling times in acceleration and deceleration respectively and
are the settling times in acceleration and deceleration respectively and 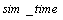 is the simulation time.Moreover, the design variables are the engine controller loop gains. In addition to the objective functions, the engine must also satisfy certain constraints. These constraints include the physical limitations of the engine and constraints placed on the response of the engine during acceleration and deceleration. The constraints are formulated as follow:
is the simulation time.Moreover, the design variables are the engine controller loop gains. In addition to the objective functions, the engine must also satisfy certain constraints. These constraints include the physical limitations of the engine and constraints placed on the response of the engine during acceleration and deceleration. The constraints are formulated as follow: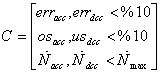
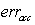 ,
,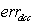 are the steady state error in acceleration and deceleration respectively,
are the steady state error in acceleration and deceleration respectively, 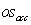 is the over shoot in accelerations,
is the over shoot in accelerations, 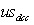 is the undershoot in deceleration and
is the undershoot in deceleration and 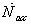 and
and 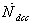 are the acceleration and deceleration respectively.The initial condition of the simulation is the GTE’s idle condition whereas the PLA command applied to the engine in the acceleration and deceleration is shown in Figure 5. As can be seen from this figure the PLA command during acceleration is set to 1.1 times the maximum speed of the engine in order to access the controllers performance in preventing the engine from over speed.
are the acceleration and deceleration respectively.The initial condition of the simulation is the GTE’s idle condition whereas the PLA command applied to the engine in the acceleration and deceleration is shown in Figure 5. As can be seen from this figure the PLA command during acceleration is set to 1.1 times the maximum speed of the engine in order to access the controllers performance in preventing the engine from over speed.
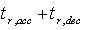 ) is in correlation with the third objective function (
) is in correlation with the third objective function (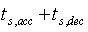 ) because it has been found that minimization of the second objective also minimizes the third objective. The reason for this outcome could be related to the linear part of the wiener structure utilized for the purpose of modeling the single spool turbo jet engine. More precisely, because a first order transfer function is chosen for the linear part of the wiener model ,if the gains of the min max structure are set in a way that switching between the different control loops are performed correctly, minimizing the rise time dose not lead to overshoot and therefore also minimizes the settling time. However considering the overshoot as a constraint is essential for obtaining reasonable optimization results. In addition it is seen from the diagonal graphs of the matrix plot that the pareto optimal solutions are almost spread uniformly on the pareto front and therefore are diverse enough to represent the entire range of the Pareto-optimal front.
) because it has been found that minimization of the second objective also minimizes the third objective. The reason for this outcome could be related to the linear part of the wiener structure utilized for the purpose of modeling the single spool turbo jet engine. More precisely, because a first order transfer function is chosen for the linear part of the wiener model ,if the gains of the min max structure are set in a way that switching between the different control loops are performed correctly, minimizing the rise time dose not lead to overshoot and therefore also minimizes the settling time. However considering the overshoot as a constraint is essential for obtaining reasonable optimization results. In addition it is seen from the diagonal graphs of the matrix plot that the pareto optimal solutions are almost spread uniformly on the pareto front and therefore are diverse enough to represent the entire range of the Pareto-optimal front. 
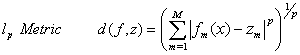
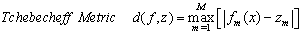

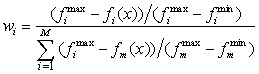
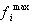 and
and 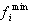 are the maximum and minimum values of each objective function respectively.
are the maximum and minimum values of each objective function respectively. 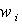 is the relative distance of each solution from its maximum value ineach objective function. Furthermore the sum of all weight components of the weight vector corresponding to a specific solutions, are equal to one. After calculating the weight vector for each solution, the solution which has a weight vector closer to the user- preferred weight vector is chosen.The ideal point and the pareto optimal point for the current problem is shown in Figure 8. The preferred Pareto-optimal solution’s obtained based on the compromise programing approach and using different distance metrics are also shown in this figure. Furthermore, Figure 9 shows the pareto optimal front and the weights of some of the optimal solutions based on the pseudo-weight vector approach. In addition to the solutions picked by the compromise programing approach, three more solutions are picked based on the pseudo-weight vector approach and are shown in table 2. In addition table 2 shows the objective functions, constraint values and the design variables corresponding for each preferred solution.
is the relative distance of each solution from its maximum value ineach objective function. Furthermore the sum of all weight components of the weight vector corresponding to a specific solutions, are equal to one. After calculating the weight vector for each solution, the solution which has a weight vector closer to the user- preferred weight vector is chosen.The ideal point and the pareto optimal point for the current problem is shown in Figure 8. The preferred Pareto-optimal solution’s obtained based on the compromise programing approach and using different distance metrics are also shown in this figure. Furthermore, Figure 9 shows the pareto optimal front and the weights of some of the optimal solutions based on the pseudo-weight vector approach. In addition to the solutions picked by the compromise programing approach, three more solutions are picked based on the pseudo-weight vector approach and are shown in table 2. In addition table 2 shows the objective functions, constraint values and the design variables corresponding for each preferred solution.



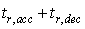 ) and third (
) and third (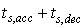 ) objectives however this minimization comes at the price of having a maximum fuel consumption as is seen in figure 12 on the other hand all the other chosen solutions have a better fuel consumption but their response is slower in comparison to the solution chosen by the L1 metric. These results confirm the correlation between rise time and settling time and the trade-off nature between these two objective and fuel consumption. Choosing a large weight for the fuel component of the weight vector in the pseudo-weight vector approach, results in less fuel consumption as is seen in figure 12. On the other hand setting a large weight for the rise time and settling time components of the weight vector results in a faster response with the cost of an increased fuel consumption as seen in figure 12 and figure 10.
) objectives however this minimization comes at the price of having a maximum fuel consumption as is seen in figure 12 on the other hand all the other chosen solutions have a better fuel consumption but their response is slower in comparison to the solution chosen by the L1 metric. These results confirm the correlation between rise time and settling time and the trade-off nature between these two objective and fuel consumption. Choosing a large weight for the fuel component of the weight vector in the pseudo-weight vector approach, results in less fuel consumption as is seen in figure 12. On the other hand setting a large weight for the rise time and settling time components of the weight vector results in a faster response with the cost of an increased fuel consumption as seen in figure 12 and figure 10.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML