1. Introduction

Gas turbine aero-engines have played an imperative role in the reliable operation of the aircrafts. For safe operation of an aircraft, stable and limit protected operation of its GTE must be ensured. Therefore, design and fine-tuning of an appropriate control system for a GTE is required to provide the satisfactory operation of the aircraft. One of the most complexities of GTE controller design is to set the controller parameters so that the engine runs optimally. On the other hand, the industrial control strategies for GTE usually use the logical selection algorithms resulting in switching and nonlinear functions[1]. Consequently, for tuning process of the controller parameters, the gradient based methods may not result in an optimized engine performance. These approaches need an initial solution which is logically close to the final solution, otherwise they trapped in a local minimum. As a result, this problem requires a non-gradient based optimization technique. In recent decades, a vast variety of non-gradient based optimization methods have been formulated, and some inspired by natural processes. Genetic algorithm[2], particle swarm optimization[3] and ant colony optimization[4] are such methods that have already been used in various real- world optimization problems[5-10]. In addition, Mehrabian and Lucas proposed the Invasive Weed Optimization (IWO) as a novel stochastic, non-gradient based algorithm inspired by the ecological behavior of colonizing weeds in 2006[11]. “In their leading research, Mehrabian and Lucas have shown the merits of IWO in finding global optimum of different complex multi-dimensional optimization problems, which reveals that IWO is an appropriate competitor for other comparatively older and well-established techniques for population-based evolutionary computation.”[12]

The aim of the present study is to investigate the use of IWO approach for GTE fuel controller gain tuning for the first time. For this purpose, an industrial fuel controller structure for a turbojet engine is firstly described. The GTE controller gain tuning is then formulated as an optimization problem based on the IWO approach where the objective function is defined to minimize the combination of the engine response time and fuel consumption. Subsequently, the results of the IWO are presented and compared with the global optimal results of dynamic programming (DP) technique in order to assess the effectiveness of the proposed approach for GTE fuel controller gain tuning. Moreover, the IWO results are compared with the results obtained from genetic algorithm (GA) to evaluate the reliability of the proposed method for using as a new metaheuristic optimization method in practical problems. Finally, the effect of optimization process on the engine performance is analyzed to study the improvement of the objective function as well as protection of the engine against physical limitations.

2. Formulation of the Optimization Problem

In this section, industrial Min-Max fuel controller design for a single spool turbojet engine is firstly described. The objective function is then prepared based on the designed controller in order to apply the IWO method.

2.1. GTE Fuel Controller Structure

Safe operation of a GTE depends on the satisfaction of its control modes. The GTE control system is designed to fulfill the pilot demand in a reasonable response time without exceeding the engine physical limitations including over-speed, over-temperature, flameout and surge in compressor. In other words, the control of a turbojet engine can be summarized by the following three different modes:

● Steady state control mode (to satisfy the pilot demand without error).

● Transient control mode (to satisfy the pilot demand in a reasonable response time).

● Physical limitation control mode (to protect the engine against over-speed, over-temperature, compressor surge and flameout).

Industrial fuel control strategies for a GTE have two main sections including steady-state controller part and transient controller part as shown in Fig.1. The steady-state controller is responsible to compute the steady state fuel flow (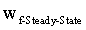) according to the engine operating condition. In this study, this part of the fuel flow is calculated by a scheduling controller as a function of the engine rotor speed. The steady state part of the controller satisfies the first engine control mode i.e. steady state control mode.

In addition to the steady-state controller, a transient controller part is considered for the control of the engine transient performance as well as the engine limitations. Transient fuel flow is the variation of the fuel flow with respect to its steady-state value. As shown in Fig.1, the structure of the controller for calculation of the transient fuel flow consists of four control loops as follow:

● Pilot lever angle (PLA) control loop; this control loop is responsible to provide the necessary transient fuel flow for satisfying the pilot demand (with gain 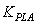). This control loop satisfies the second control mode i.e. transient control mode. The response time of the engine mainly depends on the 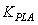variation.

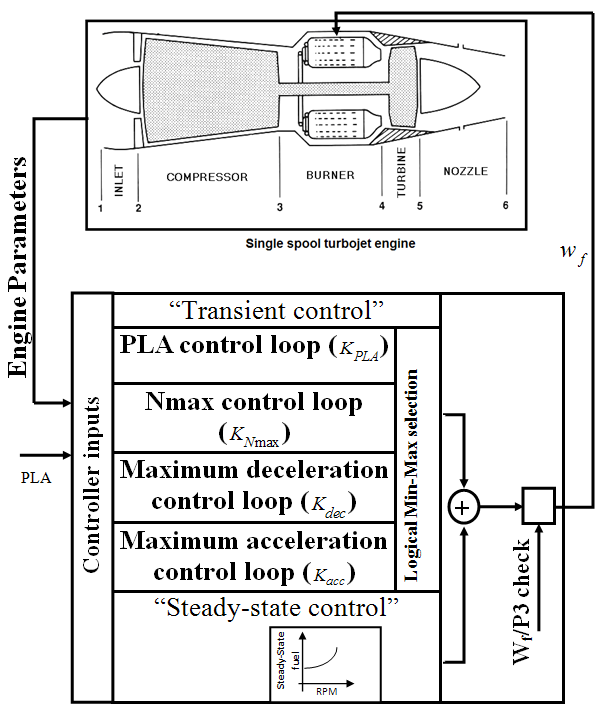Figure 1. Schematic of a GTE and fuel controller

● Maximum rotor speed (Nmax) control loop; this control loop is designed to protect the GTE against the overspeed condition in order to ensure the structural integrity of the engine spool (with gain).

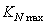● Maximum deceleration control loop; this control loop is designed to protect the engine against the flameout (with gain).

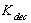● Maximum acceleration control loop; this control loop takes care of the engine aerodynamic instability including surge or stall occurrence (with gain).

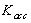It should be noted that surge is a longitudinal flow oscillation over the length of the compressor and turbine and often is due to high rotor acceleration[13]. Thus, the control of rotor speed derivative (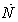control) provides surge control. In this study, the limiting bounds for the engine rotor acceleration and deceleration are found analytically and confirmed experimentally[14].

To satisfy all physical limitations, the turbine inlet temperature (TIT) should also be bounded. However, as the thermocouples usually need to shield and their responses are slow, the 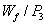ratio is widely used to control the combustion chamber output temperature as shown in Fig.1.

Using this approach, W_f/P₃ control provides good control of TIT and satisfies the combustion chamber overtemperature limitation.

The Nmax control loop, acceleration and deceleration control loops and Wf/P3 saturation satisfy the third engine control mode i.e. physical limitation control mode.

Finally, in order to select the appropriate transient control loop at any time instance, a Min-Max logical algorithm is used as follow:

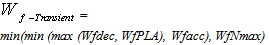(1)

where WfPLA, Wfdec, Wfacc and WfNmax are the transient fuel flow rates calculated by the PLA, maximum deceleration, maximum acceleration and maximum speed control loops, respectively.

Using the above strategy, in an acceleration operation, the min-select strategy will protect the engine from surge and over speed whereas in a deceleration process, the max-select strategy will protect the engine against flame out. If the calculated pilot command transient fuel (WfPLA) does not exceed physical limitations, it will be the winner of the Min-Max selection strategy. Otherwise, one of the limitation fuels will be selected as the transient fuel flow in order to protect the engine against failure or malfunctions.

The total fuel flow for the GTE is then calculated by adding the transient and steady-state fuel flow at any time instance as follows:

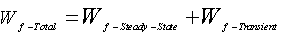(2)

2.2. Initial Gain Values

In order to select the initial gain values for the four transient control loops, the tuning process is carried out as follows:

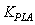The PLA loop gain () is firstly initialized to achieve a preliminary response time. In order to improve the engine response time, 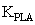is then increased until the process begins to oscillate.

In order to select the initial gain values for the four transient control loops, the tuning process is carried out as follows:

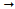In order to protect the engine against surge, 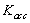is changed until the maximum rotor speed derivative (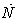) is limited to an allowable value.

In order to select the initial gain values for the four transient control loops, the tuning process is carried out as follows:

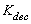is changed until the minimum rotor speed derivative (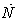) is limited to an allowable value. Consequently, the engine is protected against flameout.

In order to select the initial gain values for the four transient control loops, the tuning process is carried out as follows:

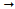In order to keep the engine integrity, 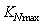is increased until the overspeed in every condition is vanished without overshoot.

The initial values obtained by the above process for a case study in Seal Level Standard (SLS) condition is shown in Table.1.

Table 1. Initial controller loop gains

2.3. Objective Function Formulation

In this study, the objective function is formulated based on the engine response time and fuel consumption to illustrate the ability of the proposed approach to optimize short terms as well as long terms objectives. Also, the physical limitations are defined as penalty functions as follows:

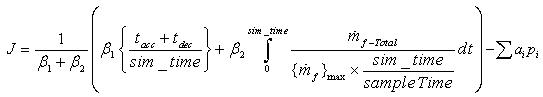(3)

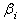As it is seen in equation (3), the objective function includes two performance indices, the engine response time and the engine fuel consumption during the defined maneuver. The performance indices are normalized first and then weighted according to their importance by coefficients. The term 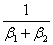guarantees that the variation of cost function value remains between o-1 if 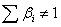. In the case that 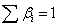there is no need to add 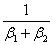to the objective function. In this paper, the weight factors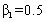, 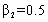are selected for the objective functions. It means that similar importance is considered for two objectives in the optimization process. In addition, 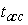and 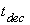are the acceleration and deceleration times which the engine requires to follow the PLA command (settling times with 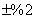error). The P_i are penalty functions including over-speed, over-temperature and violation of 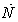during simulation (these penalty functions protect the engine from overshoots in speed and temperature as well as surge and flameout). 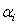are the penalty factors tuned in a trial and error manner to achieve the best results. Moreover, the design variables are the four transient control loop gains including 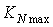, , 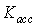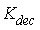and 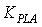as shown in Fig.1.

Taking the nonlinear and switching nature of logical selection algorithm (1) into account, the IWO is proposed for Min-Max fuel controller gain tuning in this paper.

3. Application of IWO

In this section, an overview of the IWO method is firstly presented. The method is then applied to the formulated optimization problem.

3.1. IWO Algorithm

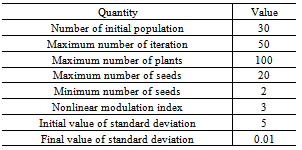
The IWO method flowchart is shown in Fig.2.a. As this figure illustrates, the method has 6 following steps:

1- Initialization a population: a population of initial solutions is firstly dispread over the d dimensional problem space with random positions. In this study, the dimension of problem is four (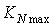,,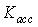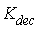and ).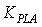

2- Fitness evaluation: each individual of population is evaluated in this step using defined objective function.

3- Reproduction: In this step, each member of the colony of weeds is allowed to produce seeds depending on its own and the colony’s lowest and highest fitness.

4- Spatial dispersal: after reproduction, the generated seeds are randomly spread over the search space according to normal distribution with a mean of zero, but varying standard deviation (SD). The variation of the SD with generation is defined as follow[13]:

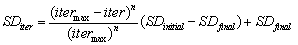(4)

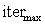Where is the maximum number of iterations and n is the nonlinear modulation index. The SD decreases from generation to generation. The decreasing rate depends on the value of the nonlinear modulation index which results in grouping fitter plants and eliminating the weaker plants[11]. Fig.2. b shows the variation of SD with generation for n=3.

5- Competitive exclusion: After reaching the maximum number of plants, the competitor exclusion mechanism activates in order to eliminate the plants with poor fitness in the generation. This mechanism is formulated so that it gives a chance to plants with lower fitness to reproduce, and if their offspring has a good fitness in the colony, then, they will survive.

6- The above steps are repeated until the maximum number of iterations is reached[15].

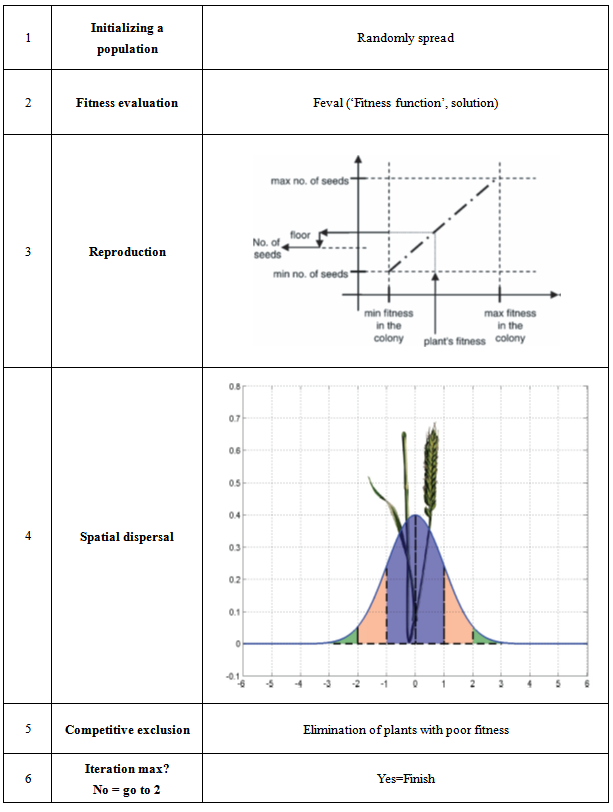Figure 2.a. IWO flowchart

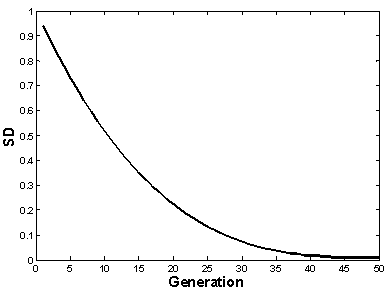Figure 2.b. variation of SD with generation in spatial dispersal step (n=3)

3.2. IWO Results

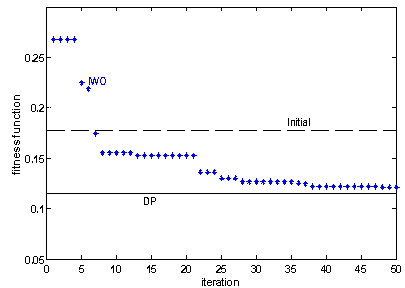Figure 3. The IWO optimization process history

Table.2 illustrates the parameters used for the IWO in this study. In order to prove the convergence of the method, the optimization process has been run several times using different parameter values. The best parameters are shown in Table.2. Using these parameters, the optimal solutions have been the same for the defined objective function in several runs that prove the convergence of the algorithm. In addition, the optimization is terminated by a prespecified number of generations.

Fig.3 shows the history of the objective function value. As shown in this figure, the optimization process converges after 37 generations. In order to show the effectiveness of the method in improvement of the defined objective function, this figure also compares the objective function value obtained from IWO method with the initial objective value which is obtained from the simulation of GTE and fuel controller in initial tuning feature. This figure clearly shows the improvement of the objective value through IWO.

Table 2. Parameters used in IWO

Moreover, the comparison between IWO objective value and the global optimum obtained from DP is shown in Fig.4. The algorithm used in this study for DP optimization of GTE fuel controller problem is developed based on the algorithm suggested by Dasgupta et al in 2006[16]. As shown in this figure, the final objective value of the IWO is reasonably close to the objective value obtained by the global solution of DP. These results confirm that IWO provides almost the global optimal value for this problem.

It should be noted that the DP method cannot evaluate the controller parameters and only gives the global optimal control signal.

3.3. Comparison between IWO and Genetic Algorithm

In order to show this fact that the IWO, as a newly developed optimization method, can be used as a good competitor for other well-established evolutionaryoptimization methods, the results obtained from this method are compared with the Genetic Algorithm (GA) results in this section. GA is a soft computing technique which can be used for optimization of the engineering problems. GA was introduced by Holland[2] as a probabilistic global search method based on the combination and generation of DNAs and Chromosomes that mimics the metaphor of natural biological evolution[17]. Table.3 compares the IWO and GA results. This table illustrates that the run time of GA is less than IWO run time. However, the IWO method has better convergence rate in comparison with GA method. In other words, the IWO method is more reliable for the problem with higher order discontinuity and talented for divergence. The cost function value for both methods is almost equal and close to global optimum obtained from DP method as shown in Table.3.

Table 3. comparison between IWO, GA and DP methods Method (average of 15 runs) Initial IWO GA DP Cost function value 0.1792 0.1204 0.1206 0.1195 Optimization time (minute) - 35:30 32:20 254 Converge at generation number - 39 48 -

4. Effect of Optimization on the GTE Performance

The IWO changes the GTE fuel controller loop gains and simulates the engine performance iteratively until the stopping criterion of the optimization problem is fulfilled. In order to verify the effectiveness of the proposed approach, the performance of the IWO optimized controller is tested for a defined pilot command. For this purpose, a computer simulation is developed for a single spool turbojet engine integrated with Min-Max fuel controller as a case study to evaluate the objective function values. The GTE model employed in this study is a Wiener model that its parameters are extracted from experimental tests. This model consists of a first order transfer function as a linear time invariant part and look-up-tables as nonlinear static part. The linear time invariant part simulates the lag of engine where the static nonlinear part gives details about the relationship between the fuel flow and the engine parameters such as rotor speed, compressor pressure ratio, exhaust gas temperature and exhaust thrust. More details about the engine modeling can be found in[18-20].

The initial condition of simulation is GTE idle condition whereas a PLA command is applied to engine during 35 seconds as shown in Fig.4. The step input is selected to simulate the worse condition for the controller.

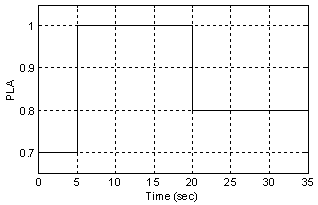Figure 4. Applied PLA for simulation

Fig.5 illustrates that the IWO method is successful in optimization of the objective function terms. This figure shows that the engine time response as well as fuel consumption are considerably decreased with IWO optimized controller.

In addition, Fig.5 shows that the IWO results are much faster in acceleration and deceleration process with almost 7% less fuel consumption comparing with the initial controller.

Moreover, the engine rotational speed (RPM) and its derivative () are depicted in Fig.6. As shown in this figure, the optimized controller satisfies the engine overspeed limitation as well as the bounds. In other words, the optimization method protects the engine against physical limitation resulting in safe operation of the engine as well as nearly global optimal performance of the engine in time response and fuel consumption.

Furthermore, Fig.6 shows that acceleration limiting loop at time t=7 sec is activated to protect the engine against surge. In other words, in IWO optimized controller, the PLA loop is firstly activated to achieve the best response time. The acceleration limiting loop is then activated at t=7sec when the 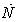reaches to the maximum allowable value.

The designed controller is optimized with a step input PLA. To show this fact that the optimized controller is improved for other inputs, the simulation is run for another PLA. For this purpose, a slope based variation of PLA is applied to the engine and controller simulation and the results are presented in Fig.7. As shown in this figure, the optimized controller tracks the input PLA in a reasonable response time without any steady state error.

Finally, it is worthwhile to mention that the IWO implementation is easier as the number of parameters is less for IWO in comparison with relatively old well-established evolutionary population-based methods like GA. Although the IWO method is slower than the GA method, it has higher convergence rate than GA. Therefore, the IWO is proposed as an appropriate candidate for gain tuning of GTE Min-Max fuel controller which is a nonlinear switching control system.

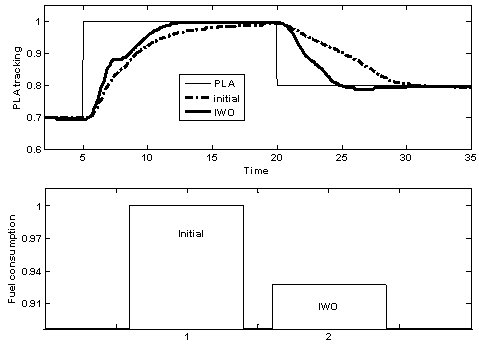Figure 5. Comparison of objective function terms in IWO and initial controller

Figure 6. Physical limitation satisfaction using IWO

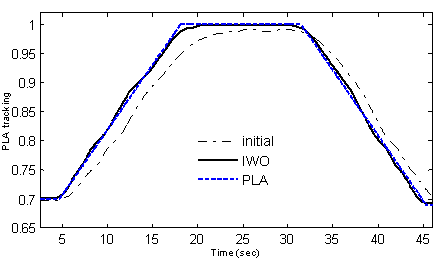Figure 7. Comparison of IWO optimized and initial controller for slope input PLA

5. Conclusions

In this paper, application of IWO technique for the GTE fuel controller gain tuning is presented. IWO as a newly developed method is applied to optimize a cost function consists of a long term objective i.e. fuel consumption, a short term objective i.e. response time and penalty functions in order to achieve an acceptable performance for the GTE and to protect the engine against physical limitations. The results illustrate that the IWO solution is reasonably close to the global optimum obtained from DP method. In addition, the simulation of GTE and optimized controller show that the IWO controller outperforms the initial controller in all objective function terms. The results confirm that in comparison with GA, the IWO runs slower but converges faster. Consequently, IWO can be successfully used for the optimization of the GTE Min-Max fuel controller parameters, resulting in an improved engine performance as well as the protection of the engine against physical limitations.

Nomenclature