1. Introduction

Sliding mode control (SMC) is a form of Variable Struc- ture Control (VSC). SMC is a nonlinear control method that alters the dynamics of a nonlinear system by the application of a high-frequency switching control. The state-feedback control law is not a continuous function of time. In fact, it switches from one continuous struc- ture to another based on the current position in the state space. VSC systems are defined by a feedback control law and a decision rule [1]. The decision rule generates the feedback controller according to the assumed switching function and to the current state of the system. In sliding mode control the controller is designed to force the system state trajectories to move towards a region of the state space (sliding surface). When the sliding sur- face is reached, the resulting motion (sliding motion) is constrained to remain in a neighborhood of this region. The system slides along it until it achieves the desired equilibrium point. As the control law is a discontinu- ous function, the sliding motion can be reached in finite time. When the sliding motion occurs, the system becomes insensitive to matched internal and external dis- turbances.

VSC and SMC theory is based on the work developed in the 1960s by Soviet scientists Emelyanov [2] [3] and Barbashin [4] [5] [6]. The contribution of Aizerman [7] [8], Itkis [9] and in particular Utkin (for instance [10] [11] [12] [13] [14]) helped the diffusion of this technique. Ap- plications of sliding mode control include robotics [15] [16], power systems [17] [18] [19], aircraft control [20] [21] and many others. Sliding mode method solves many of the disadvantages of designing a nonlinear control sys- tem. In fact, as well described by [22], commonly the nonlinear design procedure consists in applying a lin- ear control law to a system linearized about an operat- ing point. Such a controller does not guarantee optimal performance, in particular when the system state is far from the design condition. SMC, instead, allows syn- thesis of high order MIMO nonlinear systems (a good tutorial is represented [23]). Other advantages include robustness against matched uncertainties and external disturbances and the possibility to design a switching function tailored to the desired behavior. On the con- trary, the chattering phenomenon, an oscillatory motion about the sliding surface, is a considerable drawback. It can cause low control accuracy, energy loss, high wear of moving mechanical parts, plant damage and excitation of unmodeled dynamics [18] [24].

In this paper a sliding mode controller is designed to suppress the wing rock, a flight mechanics phenomenon. Wing rock is an oscillatory rolling motion of an aircraft which occurs at high angles of attack. The main aerody- namic parameters of wing rock are: (i) angle of attack (ii) angle of sweep (iii) leading edge extensions (iv) slen- der forebody. Therefore, the aircraft that are susceptible to the wing rock phenomenon are those containing these parameters; such as aircraft with highly swept wings operating with leading edge extensions. The motion is characterized by an increase in amplitude up to a limit cycle; the final state is usually stable and defined by large roll oscillations. The onset of wing rock is related with a nonlinear variation of roll damping with angles of attack and sideslip, oscillation frequency and amplitude. The control of wing rock is a relevant issue as high-speed civil transport and combat aircraft can encounter it in their flight envelope, seriously compromising handling qualities and maneuvering capabilities.

Different controllers have been proposed to suppress wing rock oscillations. Cao [25] used an adaptive con- troller, while Liu (for instance [26][27][28]) adopted dif- ferent approaches applied to the same analytical model. Another reference ([29]) dealing with nonlinear syner- getic optimal controllers applies this technique for the suppression of wing rock. An interesting paper by Lin and Hsu [30] compares Supervisory Recurrent Fuzzy Neural Network Control (SRFNNC) with SMC for wing rock control. The authors demonstrate the superiority of trained SRFNNC in tracking a reference signal, while untrained SRFNNC compared to SMC shows larger transient responses and control effort. A more com- plex controller is proposed by the same authors in [31]. Equipped with a Robust Adaptive Fuzzy Sliding Mode Control (RAFSMC) feature, robustness and automatic adjustment of fuzzy rules are guaranteed.

The choice of SMC for the design of a wing rock sup- pression system is motivated by several considerations. The wing rock model is nonlinear with quite large parametric changes in the angle of attack range: amplitude and frequency of the oscillatory limit cycle, and the related coefficients of the parametric model, change quite significantly. SMC exhibits low sensitivity to plant pa- rameter uncertainty and, generally, it requires greatly reduced-order modeling of plant dynamics. Further- more, robustness is a prerequisite to withstand model uncertainties. As a matter of fact, wing rock dynamics is dominated by wing-body vortical patterns, aerodynamic asymmetries and other sources of couplings, such as unsteady interaction between primary forebody vor- tices and lifting surfaces (wing and stabilizers). The forebody-induced wing rock may be suppressed either by changing forebody cross-section and slenderness or by the adoption of forebody vortex control techniques such as movable forebody strakes (see Figure 1) or bound- ary layer suction-blowing [34]. This type of control devices differ from conventional trailing edge control, such as ailerons, and operate in a way that is more compatible with the features of SMC controllers (high-frequency switching control). Finally, SMC provides convergence within a finite time horizon, a vital feature during some aircraft maneuvers.

In this paper a simple SMC controller for wing rock suppression is designed on a plain wing analytical model. The parameters of the model reflect the result of extensive wind tunnel experimental tests. The controller is designed so that a cost function with roll angle error and control input is minimized. The resulting controller is applied to a complete wing-fuselage analytical model under a large set of angles of attack and parametric uncertainties. Similar simulations are performed with a conventional roll damper optimized to minimize both the roll angle error and the aileron deflection. The authors seek to demonstrate that such a controller is able to cancel wing rock oscillations in all conditions with satisfactory results.

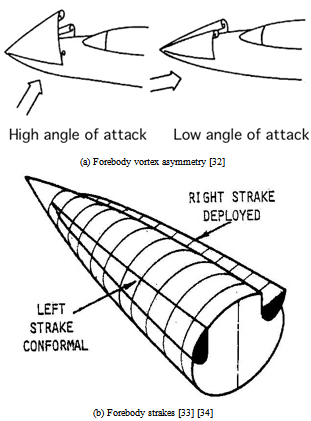Figure 1. An example of forebody vortex control device.

2. Wing Rock Model

The considered analytical model was derived and exper- imentally validated in [35] and [36]. The experimental tests were carried out in the D3M low speed wind tunnel at Politecnico di Torino. The nondimensional differential equation (single degree of freedom roll dynamics) which describes the free motion of the roll angle φ is

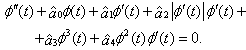(1)

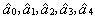where are the parameters relative to the xperiment conditions (i.e. angle of attack, Reynolds number and wing characteristics). The time derivatives are nondimensional.

The restoring moment 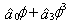exhibits a typical trend with softening of linear stiffness 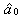(Duffing equation). As a consequence, the system is statically divergent for 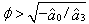. The damping coefficient 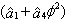is nonlinear and negative for 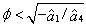(Van der Pol equation). The system is dynamically unstable for lower roll angles and becomes stable as ∅ increases up to the inversion point. The coordinate for this dynamic stability crossover is not coincident with limit cycle amplitude, as the stability of final state occurs when

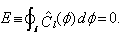(2)

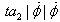This condition is required for the balance between dissipation and generation of energy E and for a stable oscillatory limit cycle. Dynamic stability and limit cycle characteristics are also influenced by the additional damping produced by the term (hydraulic damping).

Two experimental models were tested in the wind tun- nel, see Figure 2. Model A has span b = 0.169 m, root chord cr = 0.479 m and sweep Λ = 80° . Model C is 0.568 meters long with other wing characteristics remaining unchanged. Tests included free to roll conditions with airspeed V = 30 m/s (Re = 950000) and angle of attack α ranging from 25° to 45° .

Figure 2. Conguration models A (left) and C (right) tested in the wind tunnel.

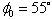Model A reaches the limit cycle regardless of the initial conditions (see the phase plane representation based on experimental data in Figure 3a.) up to a release roll angle of i.e. even for initial conditions external to the final limit cycle. The phenomenon is dominated by nonlinear damping. A simulation of the roll angle time history for model A, based on the analytical model developed in [35] and [36], is presented in Figure 4 for an angle of attack 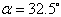. Small initial disturbances (and ) are able to trigger the wing rock motion and after a few seconds the final oscillatory behavior is achieved.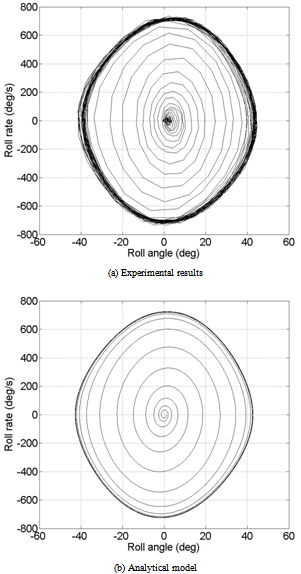

Figure 3. Phase plane free motion for model A; α=32.5°;∅0=1°;∅0=0°/s

Result for model C appear in Figure 5. In this case more complex wing rock dynamics appear because of an unsteady interaction between forebody vortices and the lifting surfaces. The apex of the fuselage generates a pair of vortices which separates from the body along its leeward fore part. These vortices tend to become asymmet- ric when the angle of attack α exceeds the fuselage apex angle due to ogive surface micro-asymmetries. Unbal- anced interference with lifting surfaces determines the typical wing rock oscillatory motion. Model C needs a longer transient than model A to convergence to a limit cycle. Aerodynamic damping is increased by the fuse- lage and limit cycle oscillation amplitudes are smaller. When the angle of attack has the value α = 27.5° wing rock is not triggered. The model settles to a nonoscillatory steady state caused by the interference be- tween the forebody and wing vortices that cancels out the hysteresis of the wing vortex normal displacement. For angles of attack greater than 37.5° the starting of wing vortices breakdown causes the oscillations amplitude to fluctuate or the motion to disappear. 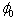Occasionally the initial release roll angle prevents the build up of oscillations; in all other cases when these are trig- gered the limit cycle is unaffected. Forebody vortices asymmetry can result in a steady state roll angle offset up to ∆∅=20° . Differently, steady state roll angle offset for model A was nonexistent. A detailed and compre- hensive analysis of the behavior of the two models can be found in [37].

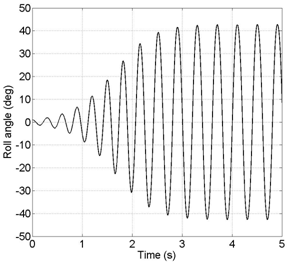Figure 4. Roll angle free motion for model A; α=32.5°;∅0=1°;∅0=0°/s

3. Controller Synthesis

Introducing the reference time ts = b/2V , Equation (1) becomes

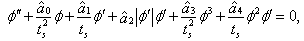including 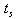in the 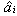coefficients it is possible to rewrite the wing rock model equation with dimensional derivatives

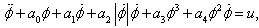(3)

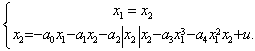(4)

A more compact form useful for further calculations is

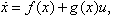(5)

where f (x) and g(x) are vector fields

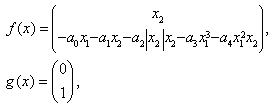and 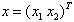is the state vector.

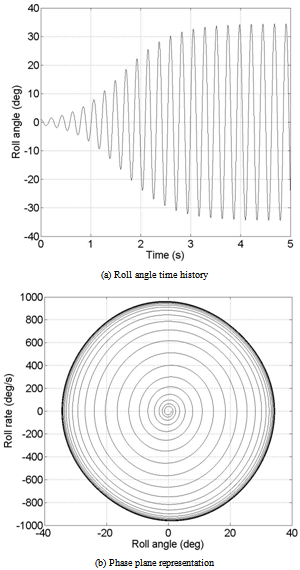Figure 5. Roll angle free motion for model C; α=32.5°;∅0=1°;∅0=0°/s

The synthesis of the controller follows the procedure described in [38]. The first step consists in an exact linearization of the model through an input/state feedback linearization. Differently from Jacobian linearization, feedback linearization is an exact representation of the original nonlinear model over a large set of operating conditions and not just an operating point. 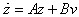This process applies a transformation z = T (x) to the system of Equation (5) so that it is reshaped into a canonical linear equivalent system with state z and controller .

Table 1. Aerodynamic Coefficients for Model A and C

The verification of the compliance of the feedback linear condition and the transformation procedure are per- formed following [24]. The resulting equivalent linear system is

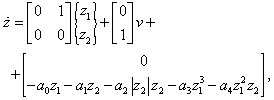which in a more compact form can be expressed as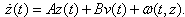

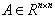and 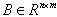are controllable matrices, the vector ω(t, z) represents the uncertainties of the equiva- lent system. The integral sliding surface for the equiva- lent linear system is chosen as

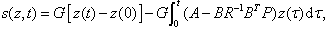(6)

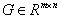where satisfies that GB is nonsingular, z(0) is the initial condition vector, 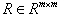is a positive definite matrix, 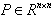is the solution of the matrix Riccati equation

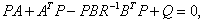(7)

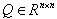where is a symmetric positive definite ma- trix. The sliding surface s(x, t) for the original nonlinear system is obtained substituting the transformation z = T (x) in Equation (6). Its derivative in time is ex- pressed in general terms as

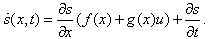The controller u of the nonlinear system is composed of two terms, a continuous term 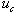and a discontinuous one 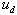so that 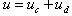. The continuous part is obtained imposing 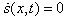, the result is

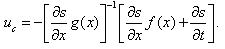(8)

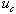The control stabilizes the system and drives its trajectories parallel to the sliding surface 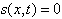. In order to force them towards the sliding surface and to eliminate the effect of uncertainties the discontinuous control law is selected

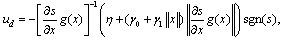(9)

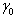where η, and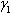 are positive constants.

The behavior of the SMC is compared with that of a much simpler controller, a proportional roll damper, commonly used in aircraft Stability Augmentation Sys- tems (SAS). Hence, a controlling torque T is included in Equation (3) so that

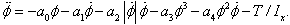(10)

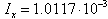kg m² is the inertia of the model,which can be considered constant between model A and model C. The torque is modeled as 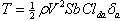where ρ = 1.225 kg/m³ is the air density, S = 0.0405 m² is the wing surface and Cl_da=-0.1 is the derivative of the roll moment coefficient with respect to the aileron deflection angle δ_a . The aileron deflection angle is con- sidered proportional to the roll rate, δ_a=kt_s∅ , where ts is introduced for dimensional reasons.

4. Implementation and Simulation Results

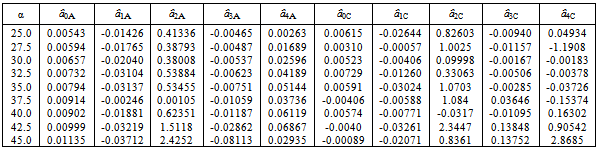
The aerodynamic parameters 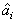of Equation (1) are found with least-squares approximation of wind tunnel experimental results (refer to Table 1.

The matrices G∈R^m×n and R∈R^m×n of Equation (6) are chosen as

G=[0,1],R=[1]

P∈R^m×n is the solution of the Riccati equation (7)

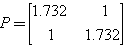where Q∈R^n×n is assumed to be an identity matrix. The parameters η, γ0 and γ1 of Equation (9) are chosen unitary.

An optimization procedure is performed in order to identify an optimal parameter for the SMC controller. A cost function considering the roll angle error and the control input is used, fSM C = τ φ2 + (1 − τ )u2 . A similar design is carried out for the roll damper, here the cho- sen function is fk = τ φ2 + (1 − τ )δa 2 where the aileron deflection angle is considered. The value of τ is set for both models to 0.8 in order to give more importance to the tracking capability of the controller. The opti- mized parameters are a gain kQ multiplying the identity matrix Q of Equation (7) for SMC and the constant k which defines δa for the roll damper. All optimizations are performed on model A which is generally available as it represents the standard configuration employed for wing rock modeling. The obtained parameters are then applied to model C.

Simulations are performed integrating Equation (4) with a fourth order Runge-Kutta method (integration stepsize ∆t = 0.001 s), with the controller acting at each time step. They include variations in angle of attack α for both models and controllers.

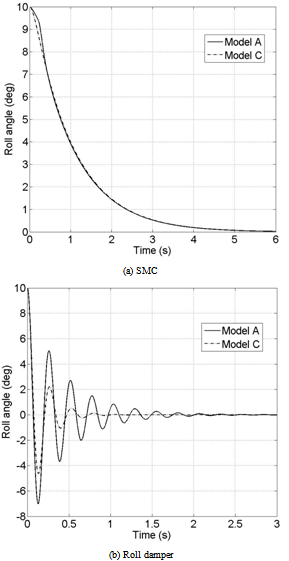Figure 6. Controlled roll angle; α=32.5°;∅0=1°;∅0=0°/s

Figure 6 shows the action on the controllers for an angle of attack α = 32.5° and initial conditions ∅₀ = 10° , ∅₀= 0° /s. The SMC controller cancels out oscillations in about 6 seconds with a smooth action. No remarkable difference is observable between model A and model C responses. On the contrary, when the roll damper is acting, model C roll angle converges to zero faster than for model A. In fact, the gain k designed on model A has a stronger effect on model C which already benefits from a larger damping effect given by the fuselage. Roll damper response is faster compared to SMC, but it still presents some oscillations.

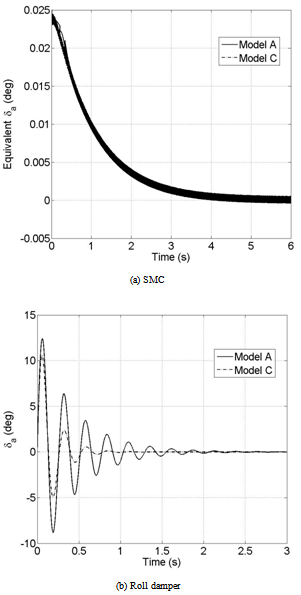Figure 7. Control action; α=32.5°;∅0=1°;∅0=0°/s

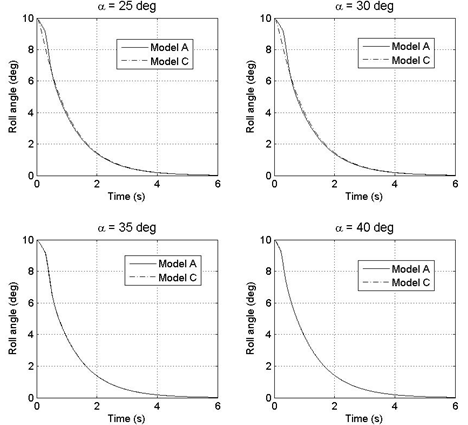Figure 8. SMC controlled roll angle for model A and C; ∅0=10°;∅0=0°/s

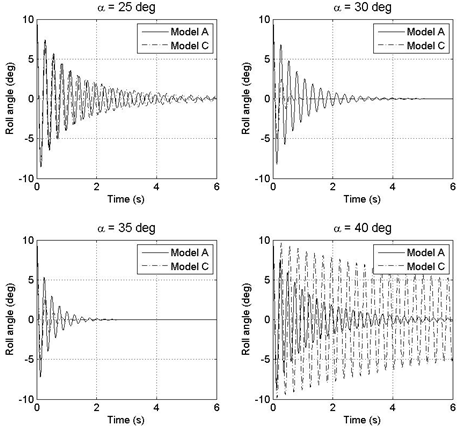Figure 9. Roll damper controlled roll angle for model A and C; ∅0=10°;∅0=0°/s

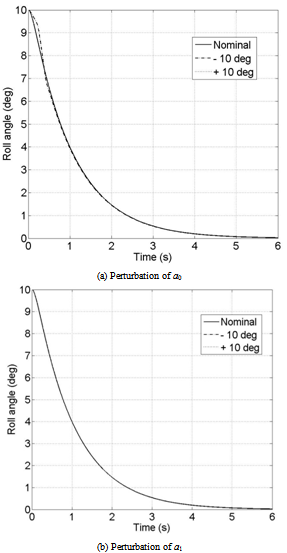Figure 10. SMC controlled roll angle with perturbations; α=32.5°; ∅0=10°;∅0=0°/s

In order to evaluate the benefit of the SMC with respect to the roll damper it would be interesting to compare the control action. Figure 7 illustrates the actual aileron deflection required by the roll damper and the equivalent deflection of a movable surface required by the SMC. Because of the different nature of the controllers, a more meaningful figure is the ratio between the total energy required to suppress the wing rock motion. This can be obtained integrating the control input along the acting time. Results show that SMC is more efficient as it employs 22.4 times less energy than the roll damper.

Figures 8 and 9 represent the responses for different angles of attack of both controllers. In all cases SMC action is unaffected by the angle of attack, and no substantial difference is observable between model A and C, in particular for large values of α.

5. Robust Assessment

One of the characteristics which makes SMC popular is its robustness to uncertainties. In the considered application this feature is important because of the difficulty in modeling accurately the wing rock motion and the response to controls. In fact, the real phenomenon is subject to the effect of aerodynamic asymmetries, couplings and wing-body vortex interactions which can hardly be modeled, even fitting experimental data. The parameters ai of Equation (3) are estimated from experimental tests. They contain a certain level of uncertainty and variability (∆∅ = ±10° ) which can alter the performance of the controller. A robust assessment of the SMC is carried out testing the controller designed on the nominal values of ai on a model where the param- eters are arbitrarily modified. In particular a₀ and a₁ are separately perturbed so that the steady state angular value of the limit cycle in the free motion reaches a ±10° offset from the nominal case. In Equation (3) the parameter a0 has the meaning of linear stiffness in the restoring moment a0 ∅ + a3 ∅3 and a1 represents a constant damping parameter of the overall damping coefficient a₁ + a₄∅² . The same analysis is performed for the roll damper and the obtained results are compared.

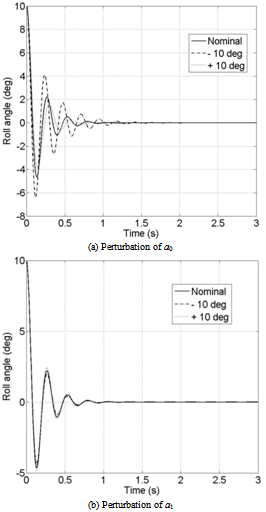Figure 11. Roll damper controlled roll angle with perturbations; α=32.5°; ∅0=10°;∅0=0°/s

6. Conclusions

In the present paper, a method to suppress wing rock through sliding mode control is proposed. Sliding mode control is chosen for its robustness with respect to model uncertainties and for its finite time convergence.

Simulations, based on an experimental parametric nonlinear model, prove the method to be effective in eliminating the unwanted rolling motion in all conditions and for different model configurations.

The results for SMC are compared with the behavior obtained with a conventional roll damper. Such controller is able to suppress the oscillatory motion, but with larger oscillations. Results suggest that an ad hoc optimization procedure for the roll damper should be implemented.

The question of compatibility of SMC with conventional servo-actuators, normally used for vehicle steering such as ailerons, still remains. The use of impulsive or discontinuous actuators (for instance movable forebody strakes or pneumatic suction-blowing devices) may over- come these limitations.

Robustness is assessed testing the controller with a simulation model altered by parametric disturbances. SMC shows excellent insensitivity to disturbances. The roll damper offers satisfying responses, but is affected by parametric changes.

As a final comment, the availability of a realistic non- linear simulation model is an attractive opportunity to validate and test, at least off line, a control design methodology developed for nonlinear mechanical systems.