-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Aerospace Sciences
p-ISSN: 2169-8872 e-ISSN: 2169-8899
2012; 1(5): 116-127
doi:10.5923/j.aerospace.20120105.04
Robust Active Vibration Control of Smart Structures; a Comparison between Two Approaches: µ-Synthesis & LMI-Based Design
Atta Oveisi1, Mohammad Gudarzi2
1Department of Mechanical Engineering, Iran University of Science and Technology, Tehran, 1684613114, Iran
2Department of Mechanical Engineering, Damavand Branch, Islamic Azad University, Damavand, Tehran, Iran
Correspondence to: Mohammad Gudarzi, Department of Mechanical Engineering, Damavand Branch, Islamic Azad University, Damavand, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The purpose of this paper is comparing the performance of two robust control designing approaches in smart structures. First, an accurate model of a homogeneous plate with special boundary conditions is derived by using of modal analysis. Then, some primitive plate’s modes are considered as nominal system and the remaining modes are left as a multiplicative unstructured modelling uncertainty. Next, two robustcontroller are designed using µ-Synthesis & LMI-Based Design approaches based on the augmented plant composed of the nominal model and its accompanied uncertainty. Finally, the robustness of two uncertain closed-loop models and the difference between two controller performances has been investigated. Obtained results show the higher performance of LMI-Based Design approach in rejection of random disturbances.
Keywords: Robust Control, Vibration Control, µ-Synthesis, LMI, A Comparison
Cite this paper: Atta Oveisi, Mohammad Gudarzi, Robust Active Vibration Control of Smart Structures; a Comparison between Two Approaches: µ-Synthesis & LMI-Based Design, International Journal of Aerospace Sciences, Vol. 1 No. 5, 2012, pp. 116-127. doi: 10.5923/j.aerospace.20120105.04.
Article Outline
1. Introduction
- The turn of mechanical, aeronautical and civil design requires structures to become lighter, more flexible and stronger, so in recent years, the light plates have been widely used in various engineering applications, such as precision machinery, aircrafts, and vehicles[1]. These requirements cause the structure to be more easily influenced by unwanted disturbances, which may lead to vibration and some problems such as fatigue, instability, performance reduction, and may even cause damage to highly stressed structures. Therefore, it has attracted many researchers in fields of structural vibration analysis, damage detection, vibration and noise control[2-4].From different kinds of control strategies consist of a purely passive control, a purely active control and a hybrid control[5],the use of active control techniques for the suppression of vibrations of very light structures is a very important target in many applications, where the additional masses of stiffeners or dampers should be avoided. Active techniques are also more suitable in cases where the disturbance to be cancelled or the properties of the controlled system vary with time[6].In practice, any structure that deforms under some loading can be regarded as flexible structure and is a distributed parameter systems. This implies that vibration at one point is related to vibration at the rest of the points over the structure. Thus, it is desirable to use appropriate sensors and actuators. Piezoelectric sensors and actuators are extensively employed in many practical applications such as smart structures due to their lightness and their capability of coupling strain and electric fields. In order to control structural vibrations, piezoelectric sensors and actuators can be easily bonded on the vibrating structure[7]. In terms of the dynamic performance and active vibration control of plates, the high-efficient dynamic modelling and appropriate control law design are the two key points. So, in recent years researchers have used different kinds of modelling methods such as finite element methods[8, 9], finite difference methods[10, 11], modal analysis[12, 13], exact mathematical modelling[14, 15], experimental analysis [16, 17], and system identification[18, 19]. Also, various types of controller design methods such as velocity feedback control[20], high gain feedback regulator[21], linear quadratic regulator (LQR) approach[22],
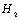 control[23],
control[23], 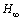 control[24], neural network control[25], fuzzy logic control[26], and intelligent algorithms[27] have been studied by former scientists. In additions, some others evaluate the performance of control algorithms in vibration suppression of flexible structure experimentally[28].In this work, an accurate model of a homogeneous plate with special boundary conditions is derived by using of modal analysis. The derived formulation can calculate transfer function from actuators voltages to sensors voltages for all plate’s modes. The obtained model has infinite number of modes, so some first modes are considered as nominal system and remaining high frequency modes are left as a multiplicative unstructured modelling uncertainty. After modelling multiplicative uncertainty, the augmented uncertain plant is obtained an optimal robust controller is designed using µ-synthesis with DK-iteration. Then, a multi-objective robust controller is designed based on the augmented plant composed of the nominal model and its accompanied uncertainty. Finally, using an algorithm for µ-analysis, robust and nominal performances of designed controllers are achieved for perturbed plants and results were compared.
control[24], neural network control[25], fuzzy logic control[26], and intelligent algorithms[27] have been studied by former scientists. In additions, some others evaluate the performance of control algorithms in vibration suppression of flexible structure experimentally[28].In this work, an accurate model of a homogeneous plate with special boundary conditions is derived by using of modal analysis. The derived formulation can calculate transfer function from actuators voltages to sensors voltages for all plate’s modes. The obtained model has infinite number of modes, so some first modes are considered as nominal system and remaining high frequency modes are left as a multiplicative unstructured modelling uncertainty. After modelling multiplicative uncertainty, the augmented uncertain plant is obtained an optimal robust controller is designed using µ-synthesis with DK-iteration. Then, a multi-objective robust controller is designed based on the augmented plant composed of the nominal model and its accompanied uncertainty. Finally, using an algorithm for µ-analysis, robust and nominal performances of designed controllers are achieved for perturbed plants and results were compared.2. Dynamic Modelling of Structure
- To design a controller that suppresses the structural vibration, one should implement an accurate model that shows the dynamic response of the flexible structure in different environmental conditions and disturbances. There are many methods, as mentioned before, to obtain dynamic model of structures. However, in homogeneous structures with special boundary conditions such as simply supported one we can use modal analysis to attain accurate models[26]. Using the modal analysis procedure, the plate transverse deflection at any point with respect to time position function
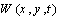 can be modelled. This function can be expanded as an infinite series, as[29]
can be modelled. This function can be expanded as an infinite series, as[29]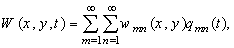 | (1) |
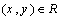 ,
, 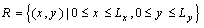 ,
, 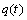 is referred to as the modal displacement or generalized coordinate and
is referred to as the modal displacement or generalized coordinate and 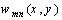 is the plate displacement modal amplitude. The mode numbers in the directions of
is the plate displacement modal amplitude. The mode numbers in the directions of 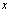 and
and 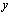 are represented by
are represented by 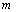 and
and 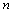 , i.e. for our case
, i.e. for our case 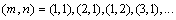 .Because of wide applications of plates in aerospace and other applied area, here a smart plate is considered to modelling.
.Because of wide applications of plates in aerospace and other applied area, here a smart plate is considered to modelling.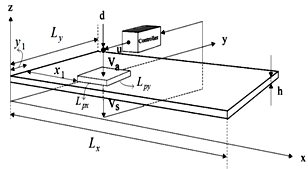 | Figure 1. A thin simply supported plate with actuator, sensor and control unit |
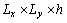 as shown in Figure 1. Piezoelectric actuator and sensor layers of dimensions
as shown in Figure 1. Piezoelectric actuator and sensor layers of dimensions 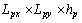 are bonded to the surface of the plate on both sides. The partial differential equation that governs the dynamics of the thin plate is[30]
are bonded to the surface of the plate on both sides. The partial differential equation that governs the dynamics of the thin plate is[30]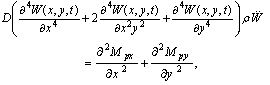 | (2) |
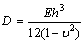 is the flexural rigidity of the plate, and
is the flexural rigidity of the plate, and 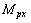 and
and 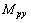 are defined as the moments generated by the piezoelectric actuating layer per unit length along
are defined as the moments generated by the piezoelectric actuating layer per unit length along 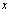 and
and 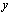 directions. For the plate,
directions. For the plate, 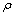 represents the mass per unit area,
represents the mass per unit area, 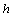 is the thickness, while
is the thickness, while 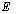 and
and 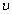 are the Young’s modulus and the Poisson’s ratio, respectively.For a simply supported plate, the following boundary conditions hold:
are the Young’s modulus and the Poisson’s ratio, respectively.For a simply supported plate, the following boundary conditions hold: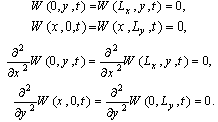 | (3) |
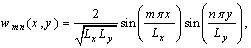 | (4) |
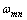 of the thin plate with the above boundary conditions satisfy[30]
of the thin plate with the above boundary conditions satisfy[30]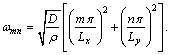 | (5) |
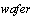 configuration [30]. This configuration assumes that the piezoelectric elements are larger in the
configuration [30]. This configuration assumes that the piezoelectric elements are larger in the 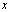 and
and 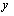 directions compared to the
directions compared to the 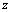 direction, i.e.
direction, i.e. 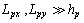 . Since the piezoelectric layers are symmetrical when a voltage is applied across the electrodes of the actuating element, it induces equal surface strains to the plate in the x and y directions, i.e.
. Since the piezoelectric layers are symmetrical when a voltage is applied across the electrodes of the actuating element, it induces equal surface strains to the plate in the x and y directions, i.e. 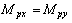 .From the modal analysis solution, the transfer function from the applied disturbance voltage
.From the modal analysis solution, the transfer function from the applied disturbance voltage 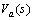 to the plate deflection
to the plate deflection 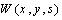 can be written as
can be written as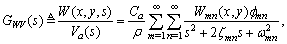 | (6) |
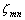 is the damping coefficient, which is normally determined experimentally, but generally is obtained by[31]
is the damping coefficient, which is normally determined experimentally, but generally is obtained by[31]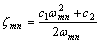 | (7) |
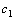 and
and 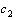 are two positive constant.
are two positive constant. 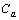 is based on the properties of the plate and the piezoelectric actuating layer:
is based on the properties of the plate and the piezoelectric actuating layer: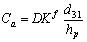 | (8) |
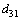 is the strain constant and
is the strain constant and 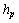 is the thickness of the piezoelectric layer.
is the thickness of the piezoelectric layer. 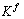 is a geometric constant which depends on the properties of the actuating layer and the plate[30]:
is a geometric constant which depends on the properties of the actuating layer and the plate[30]: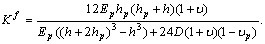 | (9) |
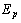 and
and 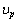 are the Young’s modulus and the Poisson’s ratio of the piezoelectric layer. Furthermore, the function term
are the Young’s modulus and the Poisson’s ratio of the piezoelectric layer. Furthermore, the function term 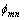 depends on the location of the actuator layer on the plate surface, such that[32]
depends on the location of the actuator layer on the plate surface, such that[32]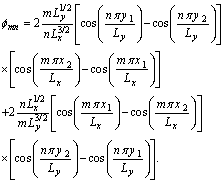 | (10) |
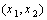 and
and 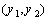 are the coordinates of a corner of the actuating layer, as shown in figure 2, such that
are the coordinates of a corner of the actuating layer, as shown in figure 2, such that 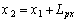 and
and 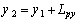 .The transfer function between the applied voltage
.The transfer function between the applied voltage 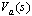 and the shunting layer output voltage
and the shunting layer output voltage 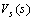 , can also be found as
, can also be found as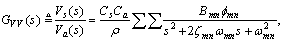 | (11) |
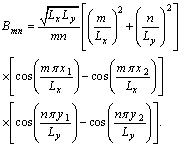 | (12) |
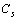 can be determined as
can be determined as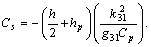 | (13) |
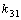 is the electromechanical coupling factor,
is the electromechanical coupling factor, 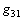 is the stress voltage coefficient, and
is the stress voltage coefficient, and 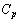 is the capacitance of the sensor piezoelectric layer.
is the capacitance of the sensor piezoelectric layer.3. Controller Design
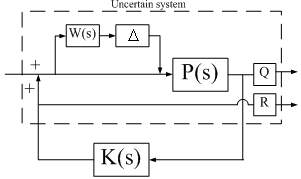
- Suppose that control input and disturbance enter through the same channel. Therefore, the closed-loop system by considering multiplicative uncertainty will be as Figure 2.
 | Figure 2. Closed-loop system with multiplicative uncertainty |
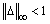 and W(s) is the weighting function for multiplicative uncertainty, that is satisfies following equation:
and W(s) is the weighting function for multiplicative uncertainty, that is satisfies following equation: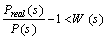 | (14) |
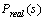 is the transfer function of the real system, by considering all or some of higher modes.
is the transfer function of the real system, by considering all or some of higher modes.3.1. µ-Synthesis
- In order to apply the general structured singular value theory to control system design, the control problem should be recast into the linear fractional transformation (LFT) setting as in Figure 3.
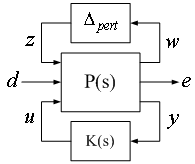 | Figure 3. LFT description of control problem |
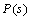 is the open-loop interconnection and contains all of the known elements including the nominal plant model, performance and uncertainty weighting functions. The
is the open-loop interconnection and contains all of the known elements including the nominal plant model, performance and uncertainty weighting functions. The 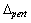 block is the uncertain element from the set
block is the uncertain element from the set 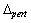 , which parameterizes all of the assumed model uncertainty in the problem.
, which parameterizes all of the assumed model uncertainty in the problem. 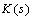 is the controller. Three sets of inputs consist of perturbation
is the controller. Three sets of inputs consist of perturbation 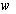 , disturbances
, disturbances 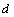 , and controls
, and controls 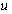 enter
enter 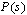 . And three sets of outputs consist of perturbation outputs
. And three sets of outputs consist of perturbation outputs 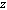 , errors
, errors 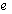 , and measurements
, and measurements 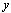 are generated. The set of systems to be controlled is described by the LFT as
are generated. The set of systems to be controlled is described by the LFT as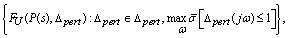 | (15) |
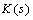 , such that for all such perturbations
, such that for all such perturbations 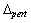 , the closed-loop system is stable and satisfies
, the closed-loop system is stable and satisfies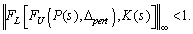 | (16) |
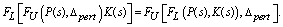 | (17) |
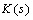 , such that for all
, such that for all 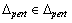 ,
, 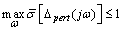 , the closed-loop system is stable and satisfies
, the closed-loop system is stable and satisfies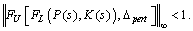 | (18) |
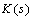 , this performance objective can be checked utilizing a robust performance test on the linear fractional transformation
, this performance objective can be checked utilizing a robust performance test on the linear fractional transformation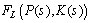 . The robust performance test should be computed with respect to an augmented uncertainty structure. The structured singular value provides the correct test for robust performance.
. The robust performance test should be computed with respect to an augmented uncertainty structure. The structured singular value provides the correct test for robust performance. 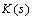 achieves robust performance if and only if
achieves robust performance if and only if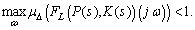 | (19) |
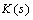 , the peak value of
, the peak value of 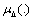 of the closed-loop transfer function
of the closed-loop transfer function 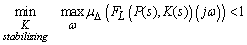 . More formally,
. More formally,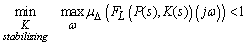 | (20) |
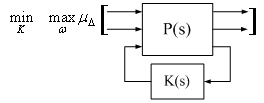 | Figure 4. µ-Synthesis concept |
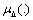 with the upper bound.For a constant matrix M and an uncertainty structure
with the upper bound.For a constant matrix M and an uncertainty structure  , an upper bound for
, an upper bound for 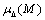 is an optimally scaled maximum singular value,
is an optimally scaled maximum singular value,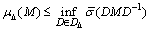 | (21) |
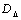 is the set of matrices with the property that
is the set of matrices with the property that 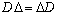 for every
for every 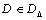 ,
, 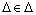 . Using this upper bound, the optimization in equation is reformulated as
. Using this upper bound, the optimization in equation is reformulated as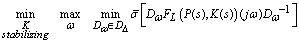 | (22) |
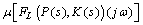 .
. 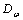 is chosen from the set of scalings,
is chosen from the set of scalings, 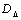 , independently at every
, independently at every  . So,
. So,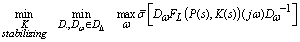 | (23) |
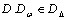 , means a frequency-dependent function D that satisfies
, means a frequency-dependent function D that satisfies 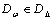 for each . The general expression
for each . The general expression 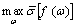 is noted as
is noted as  , giving
, giving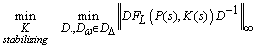 | (24) |
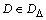 , and a complex matrix M. Suppose that U is a complex matrix with the same structure as D, but satisfying
, and a complex matrix M. Suppose that U is a complex matrix with the same structure as D, but satisfying 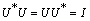 . Each block of U is a unitary (orthogonal) matrix. Matrix multiplication by an orthogonal matrix does not affect the maximum singular value, hence
. Each block of U is a unitary (orthogonal) matrix. Matrix multiplication by an orthogonal matrix does not affect the maximum singular value, hence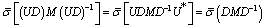 | (25) |
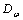 can be restricted to be a real-rational, stable, minimum-phase transfer function,
can be restricted to be a real-rational, stable, minimum-phase transfer function, 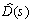 , and not affect the value of the minimum. Hence the new optimization is
, and not affect the value of the minimum. Hence the new optimization is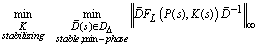 | (26) |
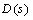 fixed at a given, stable, minimum phase, real-rational
fixed at a given, stable, minimum phase, real-rational 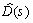 . Then, solve the optimization
. Then, solve the optimization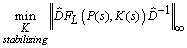 | (27) |
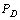 to be the system shown in Figure 6.So, the optimization is equivalent to
to be the system shown in Figure 6.So, the optimization is equivalent to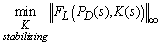 | (28) |
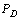 is known at this step, this optimization is precisely an
is known at this step, this optimization is precisely an 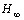 optimization control problem. The solution to the
optimization control problem. The solution to the 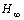 problem is well known and involves solving algebraic Riccati equations in terms of a state-space model for
problem is well known and involves solving algebraic Riccati equations in terms of a state-space model for 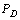 .In the second stage with K held fixed, the optimization over D is carried out in a two-step procedure:-Finding the optimal frequency-dependent scaling matrix D at a large, but finite set of frequencies (this is the upper bound calculation for µ).-Fitting this optimal frequency-dependent scaling with a stable, minimum-phase, real-rational transfer function
.In the second stage with K held fixed, the optimization over D is carried out in a two-step procedure:-Finding the optimal frequency-dependent scaling matrix D at a large, but finite set of frequencies (this is the upper bound calculation for µ).-Fitting this optimal frequency-dependent scaling with a stable, minimum-phase, real-rational transfer function 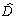 .The two-step procedure is a viable and reliable approach. The primary reason for its success is the efficiency with which both of the individual steps are carried out.
.The two-step procedure is a viable and reliable approach. The primary reason for its success is the efficiency with which both of the individual steps are carried out.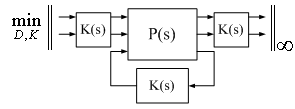 | Figure 5. Replacing µ with upper bound |
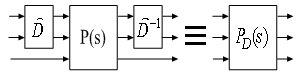 | Figure 6. Replacing rational D scaling |
3.2. LMI-Based Design
- For robust stability, we should have
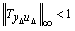 , where
, where 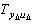 is transfer function from
is transfer function from 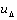 to
to 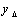 when ∆ is removed. Therefore, the
when ∆ is removed. Therefore, the 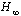 performance is appropriate for applying robustness in order to model uncertainty. However, to handle stochastic aspects such as measurement noise and random disturbance, the
performance is appropriate for applying robustness in order to model uncertainty. However, to handle stochastic aspects such as measurement noise and random disturbance, the 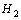 performance is functional. For appropriate disturbance rejection and control effort
performance is functional. For appropriate disturbance rejection and control effort 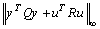 should be minimized, where Q and R are two weighting function that indicate relative importance of disturbance rejection and control effort. For minimizing performance index
should be minimized, where Q and R are two weighting function that indicate relative importance of disturbance rejection and control effort. For minimizing performance index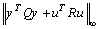 , we should minimize
, we should minimize 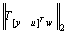 , where
, where 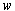 is a bounded
is a bounded 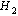 norm exogenous disturbance. The transient response of a linear system is well known to be related to the locations of its closed-loop poles. So, closed-loop system poles should be located in a appropriate region of left half plane.
norm exogenous disturbance. The transient response of a linear system is well known to be related to the locations of its closed-loop poles. So, closed-loop system poles should be located in a appropriate region of left half plane.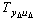 is equivalent to
is equivalent to 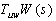 [24], so the above system can be shown as Figure 7.Now assume that a state space representation of the open-loop system in Figure 7 (by ignoring K(s)) is
[24], so the above system can be shown as Figure 7.Now assume that a state space representation of the open-loop system in Figure 7 (by ignoring K(s)) is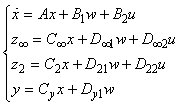 | (29) |
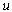 and
and 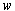 are control input and disturbance, respectively.
are control input and disturbance, respectively.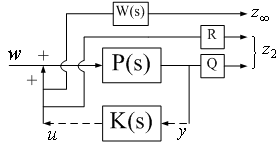 | Figure 7. Desired input and outputs of augmented plant |
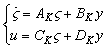 | (30) |
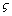 is the state variable of the controller.Therefore, the closed-loop corresponding system state-space equations containing performance and robustness channels will be as bellow
is the state variable of the controller.Therefore, the closed-loop corresponding system state-space equations containing performance and robustness channels will be as bellow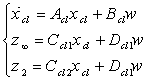 | (31) |
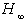 Performance: the closed-loop RMS gain from
Performance: the closed-loop RMS gain from 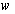 to
to  does not exceed
does not exceed 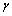 if and only if there exists a symmetric matrix
if and only if there exists a symmetric matrix 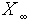 such that
such that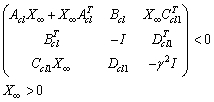 | (32) |
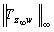 (closed-loop
(closed-loop 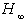 gain from disturbance to
gain from disturbance to 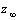 output channel)
output channel)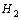 Performance: the
Performance: the 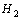 norm of the closed-loop transfer function from
norm of the closed-loop transfer function from 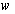 to
to 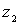 does not exceed
does not exceed 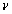 if and only if
if and only if 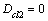 and there exist two symmetric matrices
and there exist two symmetric matrices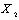 and
and 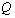 such that
such that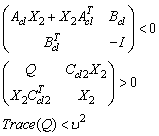 | (33) |
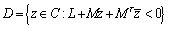 | (34) |
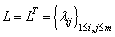 and
and 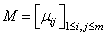 if and only if there exists a symmetric matrix
if and only if there exists a symmetric matrix 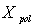 satisfying
satisfying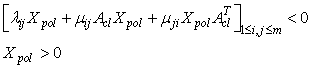 | (35) |
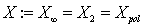 | (36) |
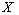 as
as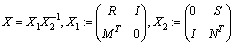 | (37) |
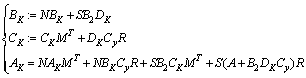 | (38) |
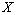 are readily turned into LMI constraints in the variables
are readily turned into LMI constraints in the variables 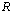 ,
,  ,
, 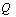 ,
, 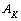 ,
, 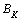 ,
, 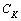 and
and 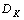 [34, 35]. This leads to the suboptimal LMI formulation of our multi-objective synthesis problem, which is defined as:Minimize
[34, 35]. This leads to the suboptimal LMI formulation of our multi-objective synthesis problem, which is defined as:Minimize 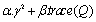 over variables
over variables 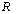 ,
,  ,
, 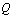 ,
, 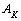 ,
, 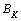 ,
, 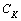 ,
, 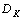 and
and 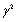 satisfying:
satisfying: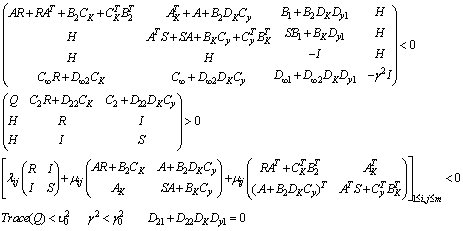 | (39) |
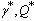 of this LMI problem, the closed-loop
of this LMI problem, the closed-loop 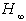 and
and 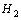 performances are bounded by
performances are bounded by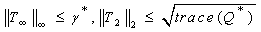 | (40) |
4. Simulation, Results and Discussion
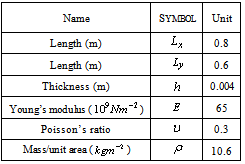
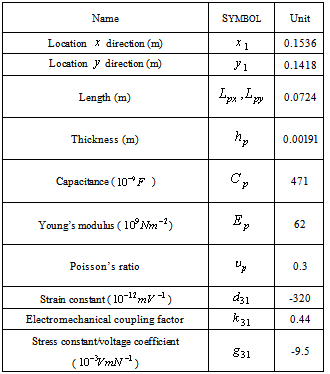
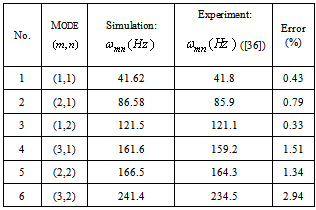
- For designing a controller, a structure consists of aluminium plate simply supported at all edges with two identical piezoelectric patches are used as an actuator and a sensor, respectively. The patches are attached symmetrically to either side of the plate, thus collocating the actuator and sensor. The plate model is shown in Figure 1. A model of the structure is obtained via modal analysis technique. Dimensions and physical properties of the plate and the piezoelectric layers are summarized in Tables 1 and 2.For verifying the obtained model, Table 3 shows the comparison of the six lowest resonant frequencies from the simulation and experiment results that is represented in[36] for two similar piezoelectric laminate plates. It is observed that the errors of the model in predicting the actual resonant frequencies vary around a few percent but the differences between the simulation and the experiment increase at higher-frequency modes. So, considering high frequencies as uncertainties eliminates this increasing error.
|
|
|
 ,
,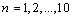 ) is shown in Figure 8.First two shape numbers (
) is shown in Figure 8.First two shape numbers (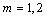 ,
,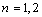 ) of this plate are considered as nominal model and other eight numbers (
) of this plate are considered as nominal model and other eight numbers (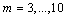 ,
,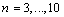 ) remain as unstructured uncertainty. So, bode diagram of the nominal model will be as figure 9.In addition, a weighting function for multiplicative unstructured uncertainty that satisfies
) remain as unstructured uncertainty. So, bode diagram of the nominal model will be as figure 9.In addition, a weighting function for multiplicative unstructured uncertainty that satisfies 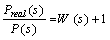 is considered. Figure 10 shows the weighting function relation to real system.
is considered. Figure 10 shows the weighting function relation to real system.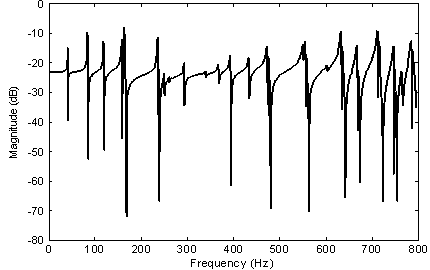 | Figure 8. Frequency response of modeled plate |
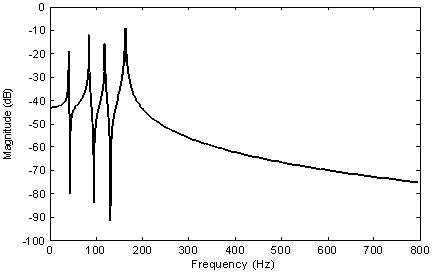 | Figure 9. Bode diagram of the nominal model |
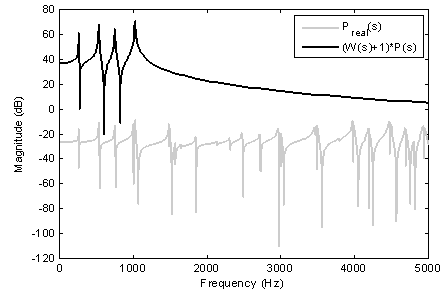 | Figure 10. The relation of weighting function to real system |
4.1. µ-Synthesis
- For designing a robust controller for mentioned smart structure using µ-Synthesis, uncertain system by multiplicative uncertainty is considered as figure 11. Two outputs consist of sensor voltage and actuator voltage by appropriate weights is considered.
 | Figure 11. Desired uncertain system used in µ-Synthesis |
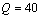 and
and 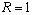 , using D-K iteration desired robust controller is obtained. This controller is of order 21. Comparison of frequency responses of closed-loop system and open-loop system is shown in Figure 12. This figure shows that the amplitude is reduced in the nominal model natural frequencies.
, using D-K iteration desired robust controller is obtained. This controller is of order 21. Comparison of frequency responses of closed-loop system and open-loop system is shown in Figure 12. This figure shows that the amplitude is reduced in the nominal model natural frequencies.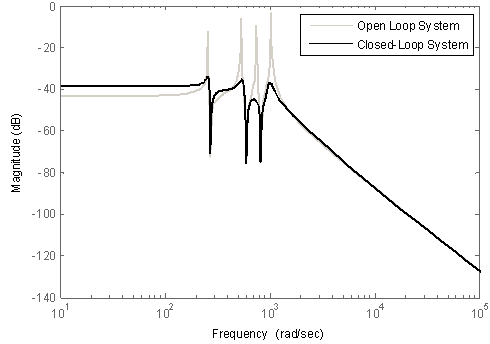 | Figure 12. Bode diagram of closed-loop system and open-loop system |
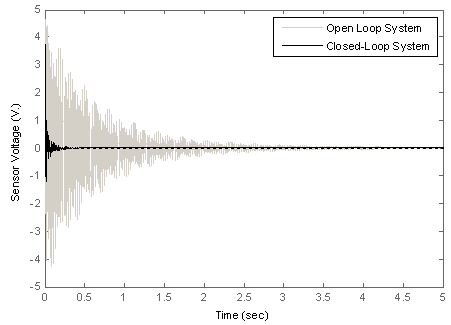 | Figure 13. Impulse response of the open-loop and closed-loop system |
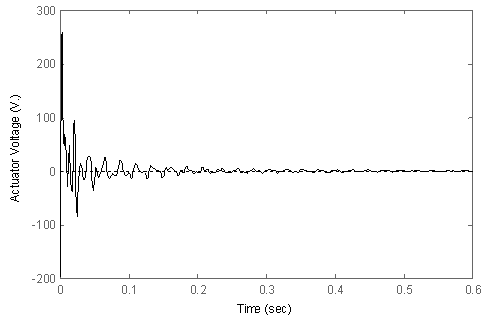 | Figure 14. Input control for impulse response of the closed-loop system |
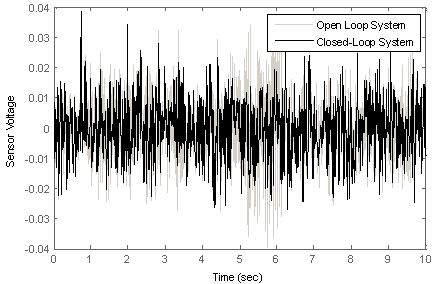 | Figure 15. Closed-loop system and open-loop system responses to a random disturbance |
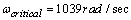 . In addition, the system can tolerate up to 140% of the modelled uncertainty without losing of desired performance. Note that robust performance guarantees robust stability of the uncertain system.
. In addition, the system can tolerate up to 140% of the modelled uncertainty without losing of desired performance. Note that robust performance guarantees robust stability of the uncertain system.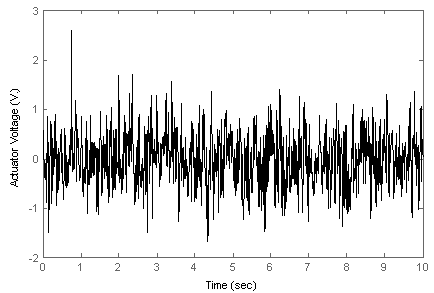 | Figure 16. Control input of closed-loop system in duration of a random disturbance |
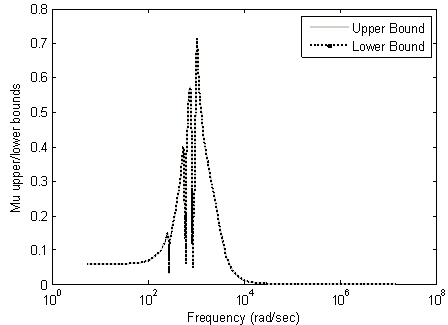 | Figure 17. µ bounds of uncertain closed-loop system |
4.2. LMI-Based Design
- Now we can design desired controller by solving convex optimization problem that was formulated in (39). For obtaining an appropriate
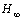 performance (robust stability) the magnitude of
performance (robust stability) the magnitude of 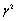 should be under unit, however it is not necessary to minimize it. But, for good performance we should minimize
should be under unit, however it is not necessary to minimize it. But, for good performance we should minimize 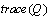 or
or 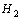 norm from exogenous disturbance to performance index, and the relative magnitudes of Q and R determine the relative importance of disturbance rejection (vibration suppression) to control effort (actuator saturation). Then, the magnitude of the constants
norm from exogenous disturbance to performance index, and the relative magnitudes of Q and R determine the relative importance of disturbance rejection (vibration suppression) to control effort (actuator saturation). Then, the magnitude of the constants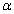 ,
,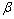 ,
, 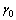 ,
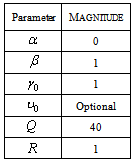
, 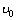 , Q and R that imply to constrains and performance index will be set as Table 4.
, Q and R that imply to constrains and performance index will be set as Table 4.
|
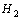 stability is the conic sector centred at the origin and with inner angle
stability is the conic sector centred at the origin and with inner angle 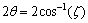 [37]. In this work, we shall take the closed-loop damping coefficient to be
[37]. In this work, we shall take the closed-loop damping coefficient to be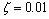 .Finally, we can obtain the desired controller by solving the convex optimization problem (39) in the MATLAB environment. Comparison of frequency responses of closed-loop system and open-loop system is shown in Figure 18. This figure shows that the amplitude is reduced in the nominal model natural frequencies.
.Finally, we can obtain the desired controller by solving the convex optimization problem (39) in the MATLAB environment. Comparison of frequency responses of closed-loop system and open-loop system is shown in Figure 18. This figure shows that the amplitude is reduced in the nominal model natural frequencies.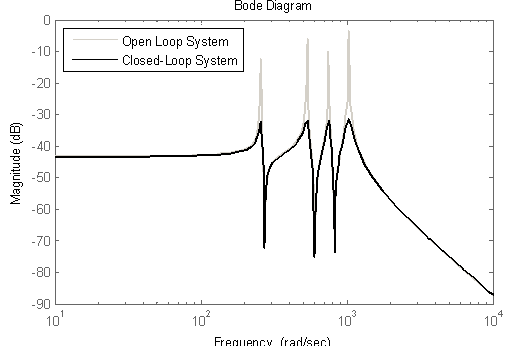 | Figure 18. Bode diagram of closed-loop system and open-loop system |
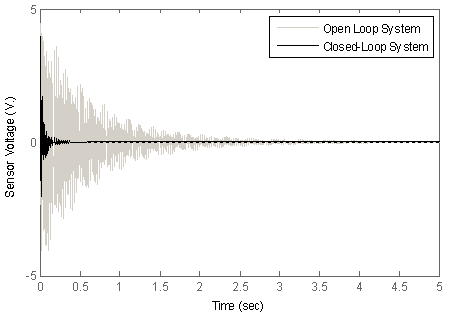 | Figure 19. Impulse response of the open-loop and closed-loop system |
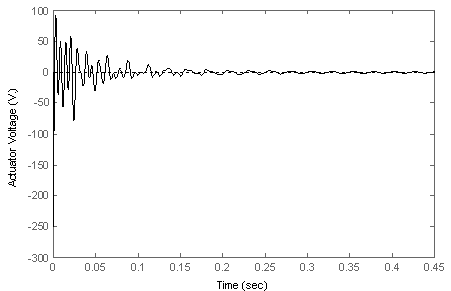 | Figure 20. Input control for impulse response of the closed-loop system |
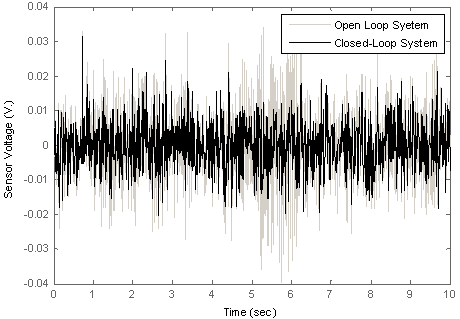 | Figure 21. Closed-loop system and open-loop system responses to a random disturbance |
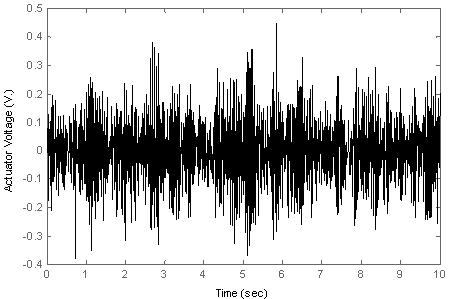 | Figure 22. Control input of closed-loop system in duration of a random disturbance |
 | Figure 23. µ bounds of uncertain closed-loop system |
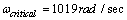 . In addition, the system can tolerate up to 146% of the modelled uncertainty without losing of desired performance. Note that robust performance guarantees robust stability of the uncertain system.
. In addition, the system can tolerate up to 146% of the modelled uncertainty without losing of desired performance. Note that robust performance guarantees robust stability of the uncertain system.4.3. A Comparison between Two Approaches
- Consider again step response of each designed controller. As one can see, designed controller using µ synthesis suppresses the structure vibration in a less time than one designed by LMI approach. Instead, actuator voltage in the first one is more than the second, so more powerful actuator is needed in the controller that designed by µ synthesis approach. Comparison of bode diagram of these two controller confirms this claim. µ bounds of two closed-loop systems are nearly similar. Therefore, two closed-loop systems can tolerate equal modelled uncertainty without losing of desired performance.However, most different between two closed-loop systems is in their response to equal random disturbances. As one can see in Figure 15 and figure 21, the performance of the LMI-based designed controller in suppression of a Gaussian random disturbance is better than one obtained by µ synthesis. Figure 24 shows this fact more clear.
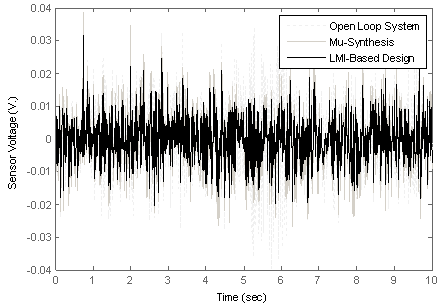 | Figure 24. Closed-loop with µ-synthesis and LMI-based design systems and open-loop system responses to a random disturbance |
- The most attractive phenomena are resulted by comparison of the actuator voltage of two systems during random disturbance applying. As one can see in Figure 16 and Figure 22, the actuator voltage of LMI-based controller is less than another one.Obtained results shows that the controller designed using LMI approach is more convenient two suppress the random vibration of a smart structure. And this because of minimizing the closed-loop
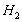 norm from disturbance to system output in LMI approach while in µ synthesis approach the closed-loop
norm from disturbance to system output in LMI approach while in µ synthesis approach the closed-loop 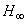 norm from disturbance to system output is minimized.
norm from disturbance to system output is minimized.5. Conclusions
- Vibration control of a simply supported, thin plate with collocated piezoelectric actuator and sensor as a general smart structure has been achieved using two different approaches of robust controller designing. In the first designing, µ synthesis approach was used. In this method an optimal robust
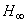 is obtained to minimize
is obtained to minimize 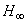 norm from disturbance input to desired output (sensor voltage and actuator voltage). LMI-based controller design is used as second method. In this approach
norm from disturbance input to desired output (sensor voltage and actuator voltage). LMI-based controller design is used as second method. In this approach 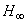 norm is used for obtaining appropriate robustness against truncated modes, whereas
norm is used for obtaining appropriate robustness against truncated modes, whereas 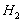 norm responsible is to obtain a good performance.Obtained results show that performance and robustness of two designed controllers are the same in the frequency domain and impulse response. However, obtained performances of two designed controllers are different under a random Gaussian disturbance. Moreover, the LMI-based controller response is obviously better than that designed by µ synthesis approach. These results show the ability of the
norm responsible is to obtain a good performance.Obtained results show that performance and robustness of two designed controllers are the same in the frequency domain and impulse response. However, obtained performances of two designed controllers are different under a random Gaussian disturbance. Moreover, the LMI-based controller response is obviously better than that designed by µ synthesis approach. These results show the ability of the 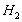 norm designing in rejection of random disturbances.Future works will be focused on two branches, first implementing these control approaches on real smart structures, experimentally. Next, by using other control approaches vibration suppression and structural acoustic active control can be investigated.
norm designing in rejection of random disturbances.Future works will be focused on two branches, first implementing these control approaches on real smart structures, experimentally. Next, by using other control approaches vibration suppression and structural acoustic active control can be investigated. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML