J. E. Jam , S. Maleki , A. Andakhshideh
Composite Materials and Technology Center, MUT, Tehran, Iran
Correspondence to: J. E. Jam , Composite Materials and Technology Center, MUT, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Linear and non-linear bending analysis of moderately thick functionally graded (FG) rectangular plates with different boundary conditions are presented using generalized differential quadrature (GDQ) method. The modulus of elasticity of plates is assumed to vary according to a power law distribution in terms of the volume fractions of the constituents. Based on the first-order shear deformation theory and Von Karman type non-linearity, the governing system of equations include a system of thirteen partial differential equations (PDEs) in terms of unknown displacements, forces and moments. To derive linear system of equations, non-linear terms are omitted in former equations. Presence of all plate variables in the governing equations provides a simple procedure to satisfy different boundary conditions. Successive application of the GDQ technique to the governing equations resulted in a system of non-linear algebraic equations. The Newton–Raphson iterative scheme is then employed to solve the resulting system of non-linear equations. Illustrative examples are presented to demonstrate accuracy and rapid convergence of the presented GDQ technique. Accuracy of the results for both displacement and stress components are verified with comparing the present results with those of analytical and finite element methods. It is found that the theory can predict accurately the displacement and stress components even for small number of grid points.
Keywords:
Non-linear, Functionally Graded, Generalized Differential Quadrature
1. Introduction
To avoid the material mismatch, a special material named ‘‘functionally graded material’’ (FGM) was proposed by a group of material scientists in Japan in[1], in which the material properties are varied smoothly and continuously from one surface to the other. The gradation of the material properties through the thickness eliminates jumps or abrupt changes in the stress and displacement distributions. The FGM is suitable for various applications, such as thermal coatings of barrier for space structures, ceramic engines, optical thin layers, biomaterial electronics, nuclear fusions, gas turbines, etc. In reality, many plate structures are subjected to high load levels that may undergo large deflections. The effect of this large deflection is to stretch the middle plane of the plate inducing membrane stresses. By this membrane action, the load carrying capacity of the plate is increased to a large extent. For plates of this kind, the governing differential equations are non-linear. The non-linearity of the governing equations may be duo to either material non-linearity or geometric non-linearity. In this paper only geometric non-linearity will be considered. This non-linearity is due to the fact that the strain displacement relations are non-linear. A considerable amount of literature exists on the non-linear analysis of rectangular plates. Zenkour[2] used generalized shear deformation theory for bending analysis of functionally graded plates. Woo and Meguid[3] provided an analytical solution for the large deflections of functionally graded plates and shallow shells under transverse mechanical loads and a temperature field using Fourier series. Yang and Shen[4] studied nonlinear bending analysis of shear deformable functionally graded plates subjected to thermo-mechanical loads. They also investigated the large deflection and postbuckling of functionally graded rectangular plates under transverse and in-plane loads by using a semi-analytical approach[5]. Tsung and Shukla[6] provided an explicit solution for the nonlinear static and dynamic responses of the functionally graded rectangular plate using the quadratic extrapolation technique for linearization, finite double Chebyshev series for spatial discretization of the variables and Houbolt time marching scheme for temporal discretization. Reddy[7] developed Navier's solutions for rectangular plates and finite element models to study the nonlinear dynamic response of FG plates using the higher-order shear deformation plate theory. Based on Reddy's higher-order shear deformation plate theory, Shen[8] also studied the nonlinear bending of a simply -supported functionally graded rectangular plate subjected to mechanical and thermal loads. Navazi et al[9] developed an analytical solution for nonlinear cylindrical bending of a functionally graded plate. In this paper it is shown that the linear plate theory is inadequate for analysis of functionally graded plate even in the small deflection range. Ghannad Pour and Alinia[10] obtained an analytical solution for large deflection of rectangular functionally graded plates under pressure loads by minimization of the total potential energy of the plate. Navazi and Haddadpour[11] presented an exact solution for nonlinear cylindrical bending of shear deformable functionally graded plates. Zhao and Liew[12] investigated the nonlinear response of functionally graded plates under mechanical and thermal loads using the mesh-free method. Barbosa and Ferriera[13] used finite element method for nonlinear analysis of functionally graded plates. Hoa et al.[14] presented an analysis on nonlinear dynamic characteristics of a simply supported functionally graded rectangular plate subjected to the transversal and in-plane excitations in time dependent thermal environment.It is well-known that analytical methods are only applicable to particular problems such as non-linear bending of FG plates with at least two opposite sides simply supported. Thus, numerical techniques, as alternatives to analytical approaches, have been developed to obtain solutions for FG plates subjected to different types of boundary conditions. Among these numerical studies, one can refer to differential quadrature (DQ)[15] and generalized differential quadrature (GDQ)[16-17]. The DQ and GDQ techniques were presented by Bellman et al[15] and Shu[16] as efficient procedures to obtain solutions of partial differential equations with relatively small number of grid points and less computational effort. The main advantage of the GDQ over DQ is its ease of the computation of weighting coefficients without any restriction on the choice of grid points. In this paper, generalized differential quadrature method is employed to obtain solutions for linear and non-linear bending analysis of moderately thick FG plates. For the assessment of the accuracy and convergence of the method, the present results are compared with those of other investigators. It is found that the GDQ method predicts accurately both the displacement and stress components.
2. Governing Equation
Consider a rectangular plate of side A,B and thickness h, shown in Fig. 1. According to the first-order shear deformation theory, the displacement field is expressed as[18]: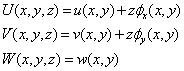 | (1) |
where u,v and w denote the displacements in x,y and z directions and 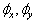 are rotations of xz and yz planes of mid-plane, respectively. The strain–displacement relations due to von Kármán-type non-linearity, can be expressed as follows[18]:
are rotations of xz and yz planes of mid-plane, respectively. The strain–displacement relations due to von Kármán-type non-linearity, can be expressed as follows[18]: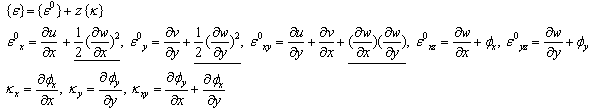 | (2) |
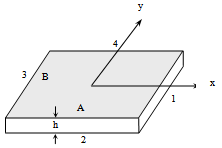 | Figure 1. Geometry of plate |
Integrating the relevant stress components through the thickness of the plate, in-plane stress resultants (Nx, Ny, Nxy), couple resultants (Mx, My, Mxy), and the transverse shear stress resultants (Qx, Qy), are obtained. Consequently constitutive equations are stated as follows[18]: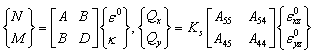 | (3a) |
where Ks is shear correction factor and in all presented results (Ks=5/6) and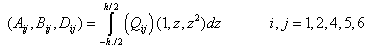 | (3b) |
For FGMs we have: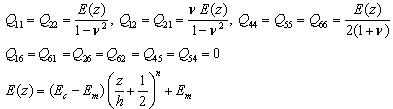 | (4) |
where c, m denote ceramic and metal, respectively.Finally, the constitutive equations for FG plates in terms of displacement and rotation components can be derived as[18]:
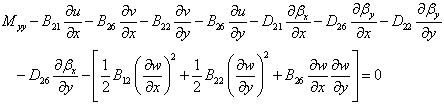 | (5) |
Using the principle of minimum total potential energy, the nonlinear equilibrium equations can be shown to be[18]: 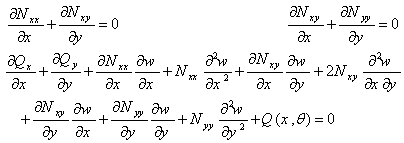
 | (6) |
Eight constitutive equations (5) and five equations of equilibrium (6) are the thirteen partial differential equations governing the nonlinear bending of FG plates. Underlined terms in equations (2) are non-linear terms which are omitted for linear analysis.
2.1. Boundary Conditions
Two different boundary conditions are considered at each edge of the plate as[18]: 1-Clamped (C):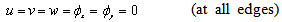 | (7) |
2-Simply supported (S): 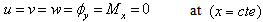 | (8a) |
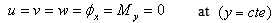 | (8b) |
3. Application of GDQ
In order to use GDQ technique the plate is divided into nx× ny grid points where (x,y) of grid points is zeros of the well-known Chebyshev polynomials[16].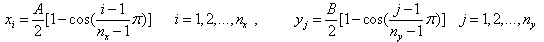 | (9) |
According to the GDQ method, the partial derivative of an unknown function with respect to a variable is approximated by a weighted sum of function values at all discrete points in that direction. Considering a function f(x) with n discrete grid points, we have[16]: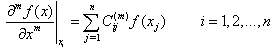 | (10) |
where xj is the discrete point in the variable domain, and f(xj) and 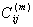 are the function values at these points and related weighting coefficients, respectively. In order to determine the weighting coefficients
are the function values at these points and related weighting coefficients, respectively. In order to determine the weighting coefficients 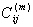 , the Lagrange interpolation basic functions are used as the test functions and explicit formulas for computing these weighting coefficients are given by[16]
, the Lagrange interpolation basic functions are used as the test functions and explicit formulas for computing these weighting coefficients are given by[16]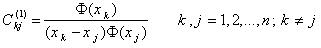 | (11) |
where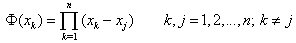 | (12) |
For the first-order derivative (i.e., m=1) and also for higher-order derivatives, one can use the following relations iteratively: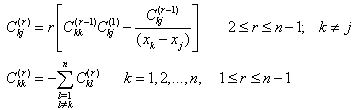 | (13) |
The next step is to discretize the governing equations based on the definitions given in (10). For example, the first equation in (5) at a sample grid point (xi, yj) can be written as: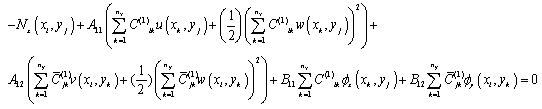 | (14) |
where (xi,yj) is a grid point inside the plate with i = 1,2,..., nx and j = 1,2,..., ny. 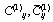 are weighting coefficients for first order partial derivatives[16]. Following the procedure explained above leads to a system of 13(nx× ny) nonlinear algebraic equations with the same number of unknowns. It should be noted that applying boundary conditions (7, 8) to the obtained algebraic equations, five of the thirteen unknown parameters at each boundary node will vanish. At last an incremental-iterative method should be used to solve the resulting nonlinear system of equations. In the present analysis, the solution algorithms are based on the Newton–Raphson method. This method yields the following linearized system of equations for the incremental solution at (r+1)th iteration[18]:
are weighting coefficients for first order partial derivatives[16]. Following the procedure explained above leads to a system of 13(nx× ny) nonlinear algebraic equations with the same number of unknowns. It should be noted that applying boundary conditions (7, 8) to the obtained algebraic equations, five of the thirteen unknown parameters at each boundary node will vanish. At last an incremental-iterative method should be used to solve the resulting nonlinear system of equations. In the present analysis, the solution algorithms are based on the Newton–Raphson method. This method yields the following linearized system of equations for the incremental solution at (r+1)th iteration[18]: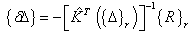 | (15) |
where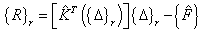 | (16) |
In Equations (15) and (16) 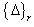 is the vector of unknowns at the rth iteration,
is the vector of unknowns at the rth iteration, 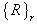 is the residual and
is the residual and 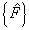 is the force vector of system of equations. The tangent stiffness matrix is defined as:
is the force vector of system of equations. The tangent stiffness matrix is defined as: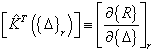 | (17) |
The total solution in (r+1)th iteration is obtained from: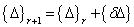 | (18) |
At the beginning of the iteration (i.e., r=0), the unknown vector is assumed to be zero (i.e., 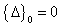 ). Due to this assumption, the solution at the first iteration is the linear solution, since the nonlinear stiffness matrix reduces to the linear one. The iteration process is continued until the difference between
). Due to this assumption, the solution at the first iteration is the linear solution, since the nonlinear stiffness matrix reduces to the linear one. The iteration process is continued until the difference between 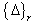 and
and 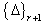 reduces to a preselected error tolerance[18]. In this study the error criterion is assumed to be:
reduces to a preselected error tolerance[18]. In this study the error criterion is assumed to be: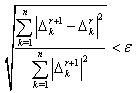 | (19) |
where n is the total number of unknowns in any GDQ nodal point and 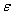 is the error tolerance.
is the error tolerance.
4. Result and Discussion
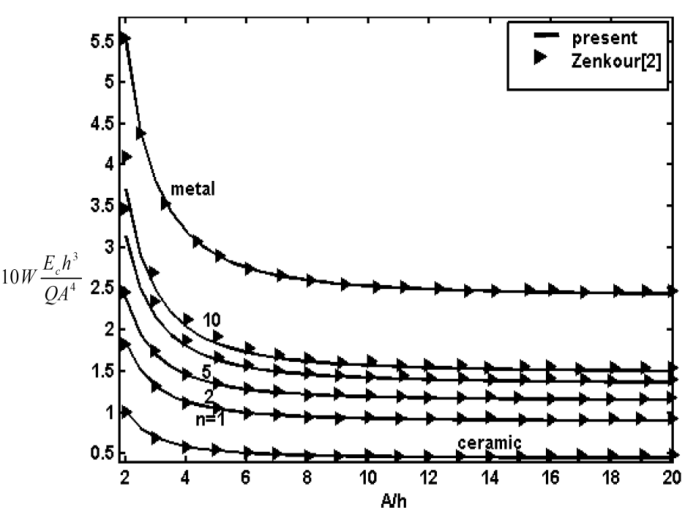
To demonstrate the efficiency and accuracy of the present method, GDQ results for both linear and non-linear bending of FG rectangular plates are validated with those of other numerical and analytical methods. In all examples the plate is considered to be constructed from Aluminum-Alumina FGM and load (Q) is considered to be uniform.First example is linear bending of fully simply FG plate. Fig. 2 shows normalized deflection of SSSS rectangular FG plate versus aspect ratio A/B in comparison with analytical results of Zenkour[2]. As well can be seen in the figure the deflection is maximum for the metallic plate and minimum for the ceramic plate. Deflection of FG plates is intermediate to that of the metallic and ceramic plates. Normalized deflection of SSSS square FG plate versus side to thickness ratio A/h is also shown in Fig. 3. It can be concluded from the figure, for thin plates the effect of thickness on non-dimensional deflection is negligible and results of first order theory is the same as classical theory.The system of equations which is used here guarantees the same order of accuracy for predictions of various stress and displacement components. In order to prove the idea variation of normalized stress in x,y direction of SSSS FG plate through the thickness is demonstrated in Figs 4, 5, respectively. The in-plane stresses are compressive throughout the lower half and tensile throughout the upper half of plate. It is illustrated that minimum value of zero for all in-plane stresses occurs at z/h=0.153 and it is independent of aspect ratio and side to thickness ratio.Second example regards to non-linear analysis for FG plates. Fig. 6 shows variation of normalized central stress of fully simply supported FG square plate of side A=200mm and thickness h=10mm through the thickness. Normalized central deflection of this plate versus load is also shown in Fig. 7. Included in these figures are also analytical results of Ghannad Pour and Alinia[10]. It is seen that the GDQ results are in good agreement with those obtained by analytical solution.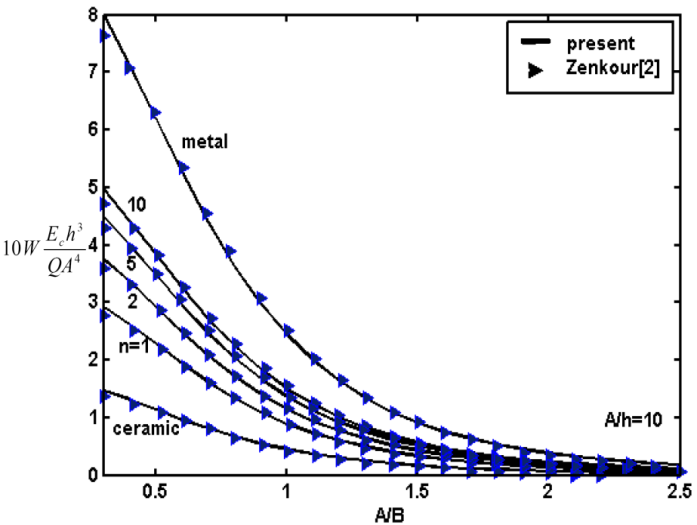 | Figure 2. Normalized deflection of SSSS FG rectangular plate versus A/B (linear analysis) |
 | Figure 3. Normalized deflection of SSSS FG square plate versus A/h (linear analysis) |
 | Figure 4. Variation of normalized stress in x direction of SSSS FG square plate (linear analysis) |
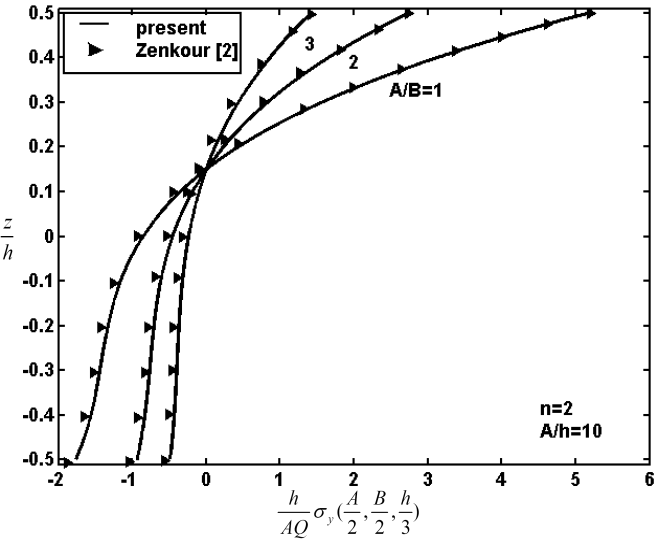 | Figure 5. Variation of normalized stress in y direction of SSSS FG rectangular plate through the thickness (linear analysis) |
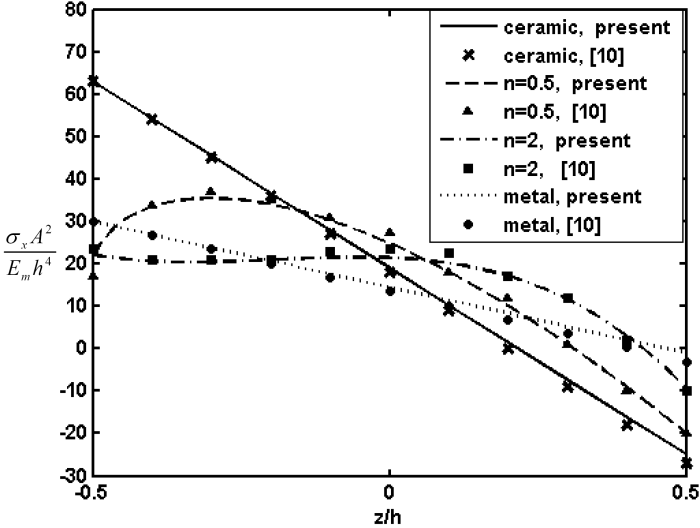 | Figure 6. Variation of normalized central stress of SSSS FG square plate through the thickness(non-linear analysis) |
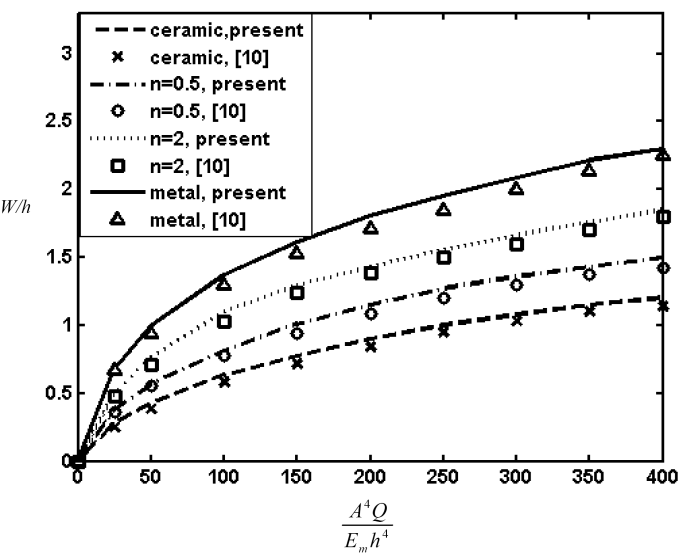 | Figure 7. Normalized central deflection of SSSS FG square plate versus load (non-linear analysis) |
As noticed before presence of all variables in system of equations provides a simple procedure to apply different boundary conditions. To define different boundary conditions the edges of the plate are numbered from 1 to 4 as shown in Fig. 1. Last examples of this study regards to non-linear analysis of SSCS and CCSS plates. Variation of normalized deflection of SSCS and CCSS square FG plate at 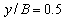 are shown in Fig. 8, 9 respectively. In this figures
are shown in Fig. 8, 9 respectively. In this figures 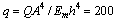 and results are validated with ABAQUS finite element results. Fig. 8 illustrate the convergence rate of method with various number of grid points. As well can be seen the method is fast convergence and the predicted results with 9×9 grid points are very good. Good accuracy of GDQ method is a noticeable point of all examples.
and results are validated with ABAQUS finite element results. Fig. 8 illustrate the convergence rate of method with various number of grid points. As well can be seen the method is fast convergence and the predicted results with 9×9 grid points are very good. Good accuracy of GDQ method is a noticeable point of all examples.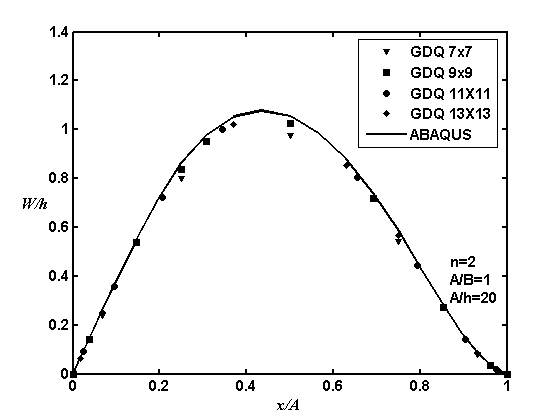 | Figure 8. Variation of normalized deflection of SSCS FG square plate at  (non-linear analysis) (non-linear analysis) |
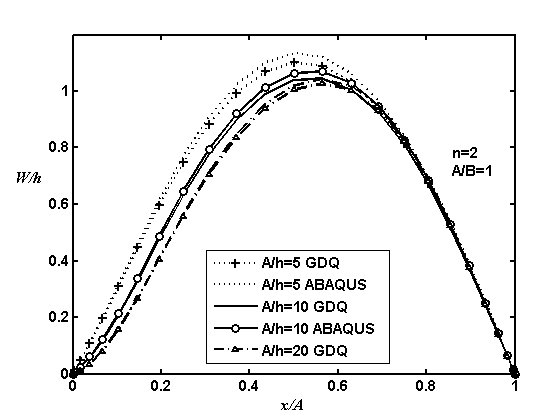 | Figure 9. Variation of normalized deflection of CCSS FG square plate at 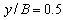 (non-linear analysis) (non-linear analysis) |
5. Conclusions
The Differential Quadrature (DQ) method is used to obtain numerical solution for linear/non-linear bending of FG plates subjected to uniformly distributed load and different boundary conditions. Comparisons of the results with those available in the literature show good agreement for both displacements and stress components. It is shown that the system equation which is used in this study provides a simple procedure to apply different boundary conditions. Results also revealed that the method is efficient and accurate and therefore, could be used for more complicated problems.
References
| [1] | Koizumi M. FGM activities in Japan. Composites 1994:28,1–4. |
| [2] | Zenkour A M. Generalized shear deformation theory for bending analysis of functionally graded plates. Applied Mathematical Modelling 2006:30,67–84. |
| [3] | Woo J and Meguid S A. Nonlinear analysis of functionally graded plates and shallow shells. International Journal of Solids and structures 2001:38,7409–7421. |
| [4] | Yang J and Shen H S. Nonlinear bending analysis of shear deformable functionally graded plates subjected to thermo-mechanical loads under various boundary conditions. Composites: Part B 2003:34,103–115. |
| [5] | Yang J and Shen H S. Non-linear analysis of functionally graded plates under transverse and in-plane loads. International Journal of Non-Linear Mechanics2003:38,467–482. |
| [6] | Tsung-Lin W U, Shukla K K and Hung J H. Nonlinear static and dynamic analysis of functionally graded plates. International Journal of Applied Mechanics and Engineering 2006:11(3),679–698. |
| [7] | Reddy J N. Analysis of functionally graded plates. International Journal for Numerical Methods in Engineering 2000:47,663-684. |
| [8] | Shen H S. Nonlinear bending response of functionally graded plates subjected to transverse loads and in thermal environments. International Journal of Mechanical Sciences 2002:44,561-584. |
| [9] | Navazi H M, Haddadpour H and Rasekh M. An analytical solution for nonlinear cylindrical bending of functionally graded plates. Thin-Walled Structures 2006:44,1129–1137. |
| [10] | GhannadPour S A M and Alinia M M. Large deflection behavior of functionally graded plates under pressure loads. Composite Structures 2006:75,67–71. |
| [11] | Navazi H.M, Haddadpour H. Nonlinear cylindrical bending analysis of shear deformable functionally graded plates under different loadings using analytical methods. International Journal of Mechanical Sciences 2008: 50,1650–1657. |
| [12] | Zhao X, Liew K.M. Geometrically nonlinear analysis of functionally graded plates using the element-free kp-Ritz method. Computer Methods in Applied Mechanics and Engineering 2009: 198,2796–2811. |
| [13] | Barbosa J A T, Ferreira A J M. Geometrically nonlinear analysis of functionally graded plates and shells. Mechanics of Advanced Materials and Structures 2010: 17,40–48. |
| [14] | Hao Y X, Zhang W, Yang J and Li S. Y. Nonlinear dynamic response of a simply supported rectangular functionally graded material plate under the time-dependent thermal mechanical loads, Journal of Mechanical Science and Technology 2011: 25 (7),1637-1646. |
| [15] | Bellman R E and Casti J. Differential quadrature and long term integration. Journal of Mathematical Analysis and Applications 1971:34, 235-38. |
| [16] | Shu C and Du H. Implementation of clamped and simply supported boundary conditions in the GDQ free vibration analysis of beams and plates. International Journal of Solids and Structures 1997:34(7),819-35. |
| [17] | Aghdam M M, Farahani R N, Dashty M and Rezaei Niya S M. Application of generalized differential quadrature method to the bending of thick laminated plates with various boundary conditions. Applied Mechanics and Materials 2006:5-6,407-414. |
| [18] | Reddy J N. Mechanics of laminated component plates and shells theory and analysis, Second edition, CRC Press, 2004. |

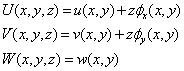
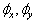 are rotations of xz and yz planes of mid-plane, respectively. The strain–displacement relations due to von Kármán-type non-linearity, can be expressed as follows[18]:
are rotations of xz and yz planes of mid-plane, respectively. The strain–displacement relations due to von Kármán-type non-linearity, can be expressed as follows[18]: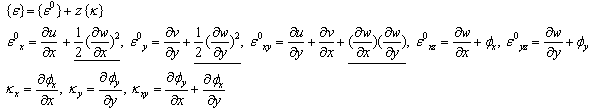

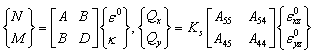
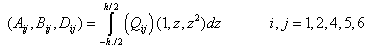
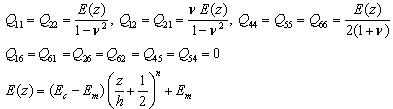

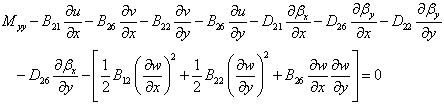
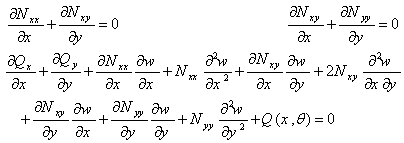

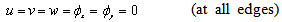
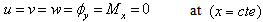
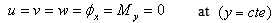
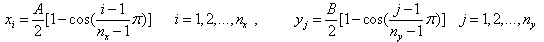
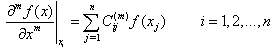
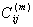 are the function values at these points and related weighting coefficients, respectively. In order to determine the weighting coefficients
are the function values at these points and related weighting coefficients, respectively. In order to determine the weighting coefficients  , the Lagrange interpolation basic functions are used as the test functions and explicit formulas for computing these weighting coefficients are given by[16]
, the Lagrange interpolation basic functions are used as the test functions and explicit formulas for computing these weighting coefficients are given by[16]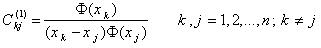
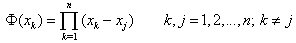
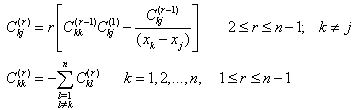
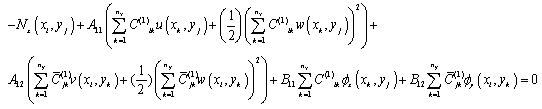
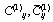 are weighting coefficients for first order partial derivatives[16]. Following the procedure explained above leads to a system of 13(nx× ny) nonlinear algebraic equations with the same number of unknowns. It should be noted that applying boundary conditions (7, 8) to the obtained algebraic equations, five of the thirteen unknown parameters at each boundary node will vanish. At last an incremental-iterative method should be used to solve the resulting nonlinear system of equations. In the present analysis, the solution algorithms are based on the Newton–Raphson method. This method yields the following linearized system of equations for the incremental solution at (r+1)th iteration[18]:
are weighting coefficients for first order partial derivatives[16]. Following the procedure explained above leads to a system of 13(nx× ny) nonlinear algebraic equations with the same number of unknowns. It should be noted that applying boundary conditions (7, 8) to the obtained algebraic equations, five of the thirteen unknown parameters at each boundary node will vanish. At last an incremental-iterative method should be used to solve the resulting nonlinear system of equations. In the present analysis, the solution algorithms are based on the Newton–Raphson method. This method yields the following linearized system of equations for the incremental solution at (r+1)th iteration[18]: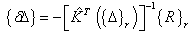
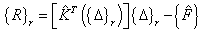
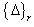 is the vector of unknowns at the rth iteration,
is the vector of unknowns at the rth iteration, 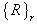 is the residual and
is the residual and 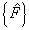 is the force vector of system of equations. The tangent stiffness matrix is defined as:
is the force vector of system of equations. The tangent stiffness matrix is defined as: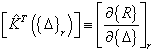
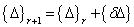
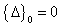 ). Due to this assumption, the solution at the first iteration is the linear solution, since the nonlinear stiffness matrix reduces to the linear one. The iteration process is continued until the difference between
). Due to this assumption, the solution at the first iteration is the linear solution, since the nonlinear stiffness matrix reduces to the linear one. The iteration process is continued until the difference between 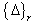 and
and 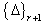 reduces to a preselected error tolerance[18]. In this study the error criterion is assumed to be:
reduces to a preselected error tolerance[18]. In this study the error criterion is assumed to be: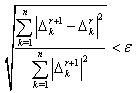
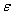 is the error tolerance.
is the error tolerance.





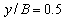 are shown in Fig. 8, 9 respectively. In this figures
are shown in Fig. 8, 9 respectively. In this figures 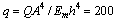 and results are validated with ABAQUS finite element results. Fig. 8 illustrate the convergence rate of method with various number of grid points. As well can be seen the method is fast convergence and the predicted results with 9×9 grid points are very good. Good accuracy of GDQ method is a noticeable point of all examples.
and results are validated with ABAQUS finite element results. Fig. 8 illustrate the convergence rate of method with various number of grid points. As well can be seen the method is fast convergence and the predicted results with 9×9 grid points are very good. Good accuracy of GDQ method is a noticeable point of all examples.
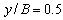 (non-linear analysis)
(non-linear analysis)
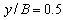 (non-linear analysis)
(non-linear analysis) Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML