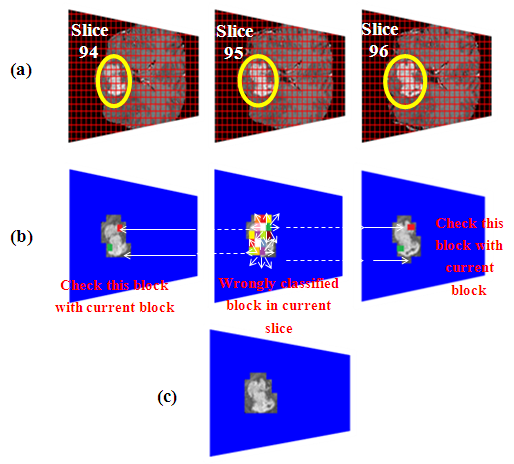
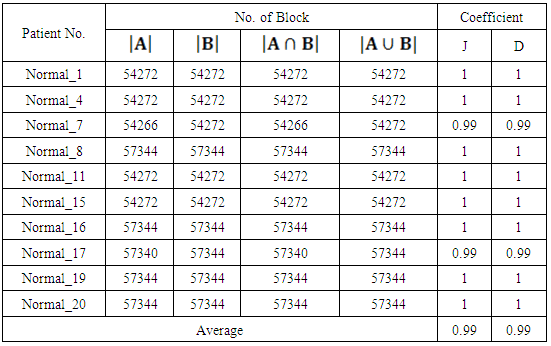
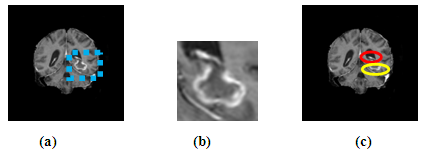
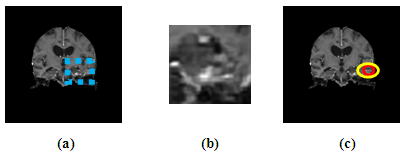
| [1] | K. Sinha and G. R. Sinha, 2014. “Efficient Segmentation Methods for Tumor Detection in MRI Images,” in Electrical, Electronics and Computer Science (SCEECS), 2014 IEEE Students’ Conference on. IEEE, pp. 1–6. |
| [2] | M. S. H. Al-Tamimi and G. Sulong, 2014. “Tumor Brain Detection Through MR Images: A Review of Literature,” J. Theor. Appl. Inf. Technol., vol. 62, no. 2, pp. 387–403. |
| [3] | M. S. H. Al-Tamimi and G. Sulong, 2014. “A Review of Snake Models in Medical MR Image Segmentation,” J. Teknol., vol. 2, no. 1, pp. 101–106. |
| [4] | J. Ferlay, H. R. Shin, F. Bray, D. Forman, C. Mathers, and D. M. Parkin, 2010. “GLOBOCAN 2008, Cancer Incidence and Mortality Worldwide: IARC Cancer Base,” Lyon, Fr. Int. Agency Res. Cancer, vol. 29, no. 10. |
| [5] | M. S. H. Al-Tamimi and G. Sulong, 2015. “A New Method for Detecting Cerebral Tissues Abnormality in Magnetic Resonance Images,” Mod. Appl. Sci., vol. 9, no. 8, pp. 363–379. |
| [6] | K. Sikka, N. Sinha, P. K. Singh, and A. K. Mishra, 2009. “A Fully Automated Algorithm under Modified FCM Framework for Improved Brain MR Image Segmentation,” Magn. Reson. Imaging, vol. 27, no. 7, pp. 994–1004. |
| [7] | S. Bourouis and K. Hamrouni, 2010. “3D Segmentation of MRI Brain Using Level Set and Unsupervised Classification,” Int. J. Image Graph., vol. 10, no. 1, pp. 135–154. |
| [8] | J. E. Iglesias, C. Liu, P. M. Thompson, and Z. Tu, 2011. “Robust Brain Extraction Across Datasets and Comparison With Publicly Available Methods,” Med. Imaging, IEEE Trans., vol. 30, no. 9, pp. 1617–1634. |
| [9] | J. Hwang, Y. Han, and H. Park, 2011. “Skull-Stripping Method for Brain MRI Using a 3D Level Set with a Speedup Operator,” J. Magn. Reson. IMAGING, vol. 34, no. 2, pp. 445–456. |
| [10] | M. A. Balafar, A. Ramli, and S. Mashohor, 2011. “Brain Magnetic Resonance Image Segmentation Using Novel Improvement for Expectation Maximizing,” Neurosciences, vol. 16, no. 3, pp. 242–247. |
| [11] | F. Rousseau, P. A. Habas, and C. Studholme, 2011. “Human Brain Labeling Using Image Similarities,” in Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference, pp. 1081–1088. |
| [12] | K. Somasundaram and T. Kalaiselvi, 2011. “Automatic Brain Extraction Methods for T1 Magnetic Resonance Images Using Region Labeling and Morphological Operations,” Comput. Biol. Med., vol. 41, no. 8, pp. 716–725. |
| [13] | O. M. Alia, R. Mandava, and M. E. Aziz, 2011. “A Hybrid Harmony Search Algorithm for MRI Brain Segmentation,” Evol. Intell., vol. 4, no. 1, pp. 31–49. |
| [14] | A. Ortiz, J. M. Górriz, J. Ramírez, and D. Salas-Gonzalez, 2011. “MR Brain Image Segmentation By Growing Hierarchical SOM and Probability Clustering,” Electron. Lett., vol. 47, no. 10, pp. 585–586. |
| [15] | G. Tian, Y. Xia, Y. Zhang, and D. Feng, 2011. “Hybrid Genetic and Variational Expectation-Maximization Algorithm for Gaussian-Mixture-Model-Based Brain MR Image Segmentation,” Inf. Technol. Biomed. IEEE Trans., vol. 15, no. 3, pp. 373–380. |
| [16] | J. Zhao, F. Q. Shao, X. D. Zhang, and C. Feng, 2012. “An Improved Integrated Active Contour Model without Re-Initialization for Vector-Valued Images Segmentation,” Adv. Mater. Res., vol. 429, pp. 271–276. |
| [17] | M. A. Balafar, 2012. “Gaussian Mixture Model Based Segmentation Methods for Brain MRI Images,” Artif. Intell. Rev., pp. 429–439. |
| [18] | L. D. Eggert, J. Sommer, A. Jansen, T. Kircher, and C. Konrad, 2012. “Accuracy and Reliability of Automated Gray Matter Segmentation Pathways on Real and Simulated Structural Magnetic Resonance Images of the Human Brain,” PLoS One, vol. 7, no. 9, pp. 1–9. |
| [19] | S. Yousefi, N. Kehtarnavaz, and A. Gholipour, 2012. “Improved Labeling of Subcortical Brain Structures in Atlas-Based Segmentation of Magnetic,” Biomed. Eng. IEEE Trans., vol. 59, no. 7, pp. 1808–1817. |
| [20] | T. Zhang, Y. Xia, and D. D. Feng, 2012. “Clonal Selection Algorithm for Gaussian Mixture Model Based Segmentation of 3D Brain MR Images,” Intell. Sci. Intell. Data Eng. pringer Berlin Heidelberg., pp. 295–302. |
| [21] | Z. Gang, Z. Dan, H. Ying, H. Xiaobo, Z. Yong, L. Weishi, and Z. Yang, 2013. “An Unsupervised Method for Brain MRI Segmentation,” Int. J. Emerg. Technol. Adv. Eng., vol. 3, no. 10, pp. 8–13. |
| [22] | M. S. H. Al-Tamimi, G. Sulong, and I. Lut, 2015. “Alpha Shape Theory for 3D Visualization and Volumetric Measurement of Brain Tumor Progression Using Magnetic Resonance Images,” Magn. Reson. Imaging, vol. 33, pp. 787–803. |
| [23] | A. Hamamci, N. Kucuk, K. Karaman, K. Engin, and G. Unal, 2012. “Tumor-Cut: Segmentation of Brain Tumors on Contrast Enhanced MR Images for Radiosurgery Applications,” IEEE Trans. Med. Imaging, vol. 31, no. 3, pp. 790–804. |
| [24] | E. D. Angelini, J. Delon, A. B. Bah, L. Capelle, and E. Mandonnet, 2012. “Differential MRI Analysis for Quantification of Low Grade Glioma Growth,” Med. Image Anal., vol. 16, no. 1, pp. 114–126. |
| [25] | Y. Megersa, 2012. “Brain Tumor Detection and Segmentation Using Hybrid Intelligent Algorithms: Design and Implementation,” Addis Ababa University, Addis Ababa Institute of Technology. |
| [26] | Rousseau, François, P. A. Habas, and C. Studholme, 2012. “A Supervised Patch-Based Approach for Human Brain Labeling,” Med. Imaging, IEEE Trans., vol. 30, no. 10, pp. 1852–1862. |
| [27] | L. Weizman, L. Ben Sira, L. Joskowicz, S. Constantini, R. Precel, B. Shofty, and D. Ben Bashat, 2012. “Automatic Segmentation, Internal Classification, and Follow-Up of Optic Pathway Gliomas in MRI,” Med. Image Anal., vol. 16, no. 1, pp. 177–188. |
| [28] | F. C. Ghesu, M. Wels, A. Jerebko, S. Michael, J. Hornegger, and B. M. Kelm, 2014. “Integrated Spatio-Temporal Segmentation of Longitudinal Brain Tumor Imaging Studies,” Med. Comput. Vision. Large Data Med. Imaging, Springer Int. Publ., pp. 74–83. |
| [29] | L. Weizman, L. Ben Sira, L. Joskowicz, D. L. Rubin, K. W. Yeom, S. Constantini, B. Shofty, and D. Ben Bashat, 2014. “Semiautomatic Segmentation and Follow-Up of Multicomponent Low-Grade Tumors in Longitudinal Brain MRI Studies,” Med. Phys., vol. 41, no. 5, p. 052303. |
| [30] | D. Zikic, B. Glocker, E. Konukoglu, and J. Shotton, 2012. “Context-Sensitive Classification Forests for Segmentation of Brain Tumor Tissues,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 1–9. |
| [31] | S. Bauer, T. Fejes, J. Slotboom, R. Wiest, L.-P. Nolte, and M. Reyes, 2012. “Segmentation of Brain Tumor Images Based on Integrated Hierarchical Classification and Regularization,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 10–13. |
| [32] | E. Geremia, B. H. Menze, and N. Ayache, 2012. “Spatial Decision Forests for Glioma Segmentation in Multi-Channel MR Images,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 14–18. |
| [33] | A. Hamamci and G. Unal, 2012. “Multimodal Brain Tumor Segmentation Using The ‘Tumor-Cut’ Method on The BraTS Dataset,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 19–23. |
| [34] | L. Zhao, W. Wu, and J. J. Corso, 2012. “Brain Tumor Segmentation Based on GMM and Active Contour Method with a Model-Aware Edge Map,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 24–27. |
| [35] | N. K. Subbanna and T. Arbel, 2012. “Probabilistic Gabor and Markov Random Fields Segmentation of Brain Tumours in MRI Volumes,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 28–31. |
| [36] | H. Shin, 2012. “Hybrid Clustering and Logistic Regression for Multi-Modal Brain Tumor Segmentation,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 32–35. |
| [37] | Y. Xiao and J. Hu, 2012. “Hierarchical Random Walker for Multimodal Brain Tumor Segmentation,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 36–40. |
| [38] | X. Tomas-Fernandez and S. K. Warfiel, 2012. “Automatic Brain Tumor Segmentation Based on a Coupled Global-Local Intensity Bayesian Model,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 41–48. |
| [39] | B. Menze and K. Van Leemput, 2012. “Segmenting Glioma in Multi-Modal Images using a Generative Model for Brain Lesion Segmentation,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 49–55. |
| [40] | B. H. Menze, E. Geremia, N. Ayache, and G. Szekely, 2012. “Segmenting Glioma in Multi-Modal Images Using a Generative-Discriminative Model for Brain Lesion Segmentation,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 56–63. |
| [41] | T. R. Raviv, K. Van Leemput, and B. H. Menze, 2012. “Multi-Modal Brain Tumor Segmentation via Latent Atlases,” Proc MICCAI-BRATS (Multimodal Brain Tumor Segmentation Challenge), pp. 64–73. |
| [42] | S. Klein, M. Loog, F. van der Lijn, T. den Heijer, A. Hammers, M. de Bruijne, A. van der Lugt, R. P. W. Duin, M. M. B. Breteler, and W. J. Niessen, 2010. “Early Diagnosis of Dementia Based On Inter subject Whole-Brain Dissimilarities,” in Biomedical Imaging: From Nano to Macro, 2010 IEEE International Symposium. IEEE., pp. 249–252. |
| [43] | E.-S. A. El-Dahshan, T. Hosny, and A.-B. M. Salem, 2010. “Hybrid Intelligent Techniques for MRI Brain Images Classification,” Digit. Signal Process., vol. 20, no. 2, pp. 433–441. |
| [44] | S. Chaplot, L. M. Patnaik, and N. R. Jagannathan, 2006. “Classification of Magnetic Resonance Brain Images Using Wavelets as Input to Support Vector Machine and Neural Network,” Biomed. Signal Process. Control, vol. 1, no. 1, pp. 86–92. |
| [45] | M. Ariffanan and M. Basri, 2008. “Medical Image Classification and Symptoms Detection Using Neuro Fuzzy,” PhD diss., Univ. Teknol. Malaysia, Fac. Electr. Eng. |
| [46] | R. Von Mises, 1964. Mathematical Theory of Probability and Statistics, Second Edi. Academic Press, Inc (London) LTD. |
| [47] | S. S. Venkatesh, 2000. The Theory of Probability: Explorations and Applications, First Edit. United Kingdom, Cambridge: Cambridge University Press, 2013. |
| [48] | V. Kuperman, Magnetic Resonance Imaging: Physical Principles and Applications, vol. 23, no. 2. Academic Press, Inc. |
| [49] | R. B. Buxton, 2009. Introdcutin to Functional Magnetic Resonance Imaging: Principles and Techniques, Second Edi. New York - USA: Cambridge University Press. |
| [50] | P. Jaccard, 1912. “The Distribution of the Flora in the Alphine Zone,” New Phytol., vol. XI, no. 2, pp. 37–50. |
| [51] | L. R.. Dice, 1945. “Measures of the Amount of Ecologic Association between Species,” Ecology, vol. 26, no. 3, pp. 297–302. |
| [52] | H. Hricak, C. G. Lacey, L. G. Sandles, Y. C. Chang, M. L. Winkler, and J. L. Stern, 1988. “Invasive Cervical Carcinoma: Comparison of MR Imaging and Surgical Findings,” Radiology, vol. 166, no. 3, pp. 623–631. |
| [53] | K. Hatano, Y. Sekiya, H. Araki, M. Sakai, T. Togawa, Y. Narita, Y. Akiyama, S. Kimura, and H. Ito, 1999. “Evaluation of the Therapeutic Effect of Radiotherapy on Cervical Cancer Using Magnetic Resonance Imaging,” Int. J. Radiat. Oncol. Biol. Phys., vol. 45, no. 3, pp. 639–644. |
| [54] | D. G. Altman and J. M. Bland, 1994. “Diagnostic Tests 1 Sensitivity and Specificity,” BMJ Br. Med. J., vol. 308, pp. 1552–1553. |
| [55] | G. Lalkhen and A. McCluskey, 2008. “Clinical Tests: Sensitivity and Specificity,” Contin. Educ. Anaesthesia, Crit. Care Pain, vol. 8, no. 6, pp. 221–223. |
| [56] | C. J. Smith, 2012. “Diagnostic Tests (1) - Sensitivity and Specificity,” Phlebology, vol. 27, no. 5, pp. 250–251. |
| [57] | and M. T. Okuda, Tomoko, Yukunori Korogi, Yoshinori Shigematsu, Takeshi Sugahara, Toshinori Hirai, Ichiro Ikushima, Luxia Liang, 1999. “Brain Lesions: When Should Recovery Sequences Be Used in MR Evaluation?,” Radiology, vol. 212, no. 3, pp. 793-798. |











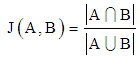
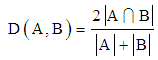
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML