1. Introduction

Parallel machines provide a wonderful opportunity for applications with large computational requirements. Effective use of these machines, though, requires a keen understanding of how they work. A major source of speedup is the parallelizing of operations. Parallel operations can be either within-processor, such as with pipelining or having several ALUs within a processor, or between processor, in which many processors work on different parts of a problem in parallel. Our focus here is on between-processor operations. Execution speed is the reason that comes to most people's minds when the subject of parallel processing comes up. But in many applications, an equally important consideration is memory capacity. Parallel processing application often tend to use huge amounts of memory, and in many cases the amount of memory needed is more than can _t on one machine. If we have many machines working together, especially in the message-passing settings described below, we can accommodate the large memory needs. Here many CPUs share the same physical memory. This kind of architecture is sometimes called MIMD, standing for Multiple Instruction (different CPUs are working independently, and thus typically are executing different instructions at any given instant), Multiple Data (different CPUs are generally accessing different memory locations at any given time)[1]. Until recently, shared- memory systems cost hundreds of thousands of dollars and were accordable only by large companies, such as in the insurance and banking industries, the high-end machines are indeed still quite expensive, but now dual-core machines, in which two CPUs share a commonplace at home. Numerous programming languages and libraries have been developed for explicit parallel programming. These differ in their view of the address space that they make available to the programmer, the degree of synchronization imposed on concurrent activities, and the multiplicity of programs. The message-passing programming paradigm is one of the oldest and most widely used approaches for programming parallel computers. Its roots can be traced back in the early days of parallel processing and its wide-spread adoption can be attributed to the fact that it imposes minimal requirements on the underlying hardware[2-4]. We first describe some of the basic concepts of the message-passing programming paradigm and then explore various message-passing programming techniques using the standard and widely-used Message Passing Interface. There are two key attributes that characterize the message-passing programming paradigm. The first is that it assumes a partitioned address space and the second is that it supports only explicit parallelization. Here we have a number of independent CPUs, each with its own independent memory. The various processors communicate with each other via networks of some kind. Large shared-memory multiprocessor systems are still very expensive. A major alternative today is networks of workstations (NOWs)[5]. Let’s investigate an example contained vector-matrix multiplication: Suppose we wish to multiply an (n*1) vector X by a (n*n) matrix A, putting the product in an (n*1) vector Y, and we have p processors to share the work. In all the forms of parallelism, each node would be assigned some of the rows of A, and would multiply X by them, thus forming part of Y. Note that in typical applications, the matrix A would be very large, say thousands of rows and thousands of columns. Otherwise the computation could be done quite satisfactorily in a sequential, i.e. nonparallel manner, making parallel processing unnecessary. In implementing the matrix-vector multiply example in the shared-memory paradigm, the arrays for A, X and Y would be held in common by all nodes. Computation of the matrix-vector product AX would then involve the nodes somehow deciding which nodes will handle which rows of A. Each node would then multiply its assigned rows of A times X, and place the result directly in the proper section of Y. Today, programming on shared-memory multiprocessors is typically done via threading. A thread is similar to a process in an operating system (OS), but with much less overhead. Threaded applications have become quite popular in even uni processor systems, and Unix, Windows, Python, Java and Perl all support threaded programming. Important note: Effective use of threads requires a basic understanding of how processes take turns executing[6]. The logical view of a machine supporting the message-passing paradigm consists of p processes, each with its own exclusive address space. Instances of such a view come naturally from clustered workstations and non-shared address space multi computers. There are two immediate implications of a partitioned address space. First, each data element must belong to one of the partitions of the space; hence, data must be explicitly partitioned and placed. This adds complexity to programming, but encourages locality of access that is critical for achieving high performance on non-UMA architecture, since a processor can access its local data much faster than non-local data on such architectures. The second implication is that all interactions (read-only or read/write) require cooperation of two processes – the process that has the data and the process that wants to access the data. In particular, for dynamic and/or unstructured interactions the complexity of the code written for this type of paradigm can be very high for this reason. However, a primary advantage of explicit two-way interactions is that the programmer is fully aware of all the costs of non-local interactions, and is more likely to think about algorithms (and mappings) that minimize interactions. Another major advantage of this type of programming paradigm is that it can be efficiently implemented on a wide variety of architectures. The message-passing programming paradigm requires that the parallelism is coded explicitly by the programmer. That is, the programmer is responsible for analyzing the underlying serial algorithm/application and identifying ways by which he or she can decompose the computations and extract concurrency. As a result, programming using the message-passing paradigm tends to be hard and intellectually demanding. However, on the other hand, properly written message passing programs can often achieve very high performance and scale to a very large number of processes.

2. Structure of Message-Passing

Message-passing programs are often written using the asynchronous or loosely synchronous paradigms. In the asynchronous paradigm, all concurrent tasks execute asynchronously. This makes it possible to implement any parallel algorithm. However, such programs can be harder to reason about, and can have nondeterministic behavior due to race conditions. Loosely synchronous programs are a good compromise between these two extremes. In such programs, tasks or subsets of tasks synchronize to perform interactions. However, between these interactions, tasks execute completely asynchronously. Since the interaction happens synchronously, it is still quite easy to reason about the program. Many of the known parallel algorithms can be naturally implemented using loosely synchronous programs. In its most general form, the message-passing paradigm supports execution of a different program on each of the p processes. This provides the ultimate flexibility in parallel programming, but makes the job of writing parallel programs effectively unscalable. For this reason, most message - passing programs are written using the single program multiple data (SPMD) approach. In SPMD programs the code executed by different processes is identical except for a small number of processes (e.g., the "root" process). This does not mean that the processes work in lock-step. In an extreme case, even in an SPMD program, each process could execute a different code (the program contains a large case statement with code for each process). But except for this degenerate case, most processes execute the same code. SPMD programs can be loosely synchronous or completely asynchronous[7].

3. Classification of Shared Memory and Message Passing

Any computer, whether sequential or parallel, operates by executing instructions on data. A stream of instructions (the algorithm) tells the computer what to do at each step. A stream of data (the input to the algorithm) is affected by these instructions. Depending on whether there is one or several of these streams, we can distinguish among four classes of computers: Single Instruction stream, Single Data stream (SISD), Multiple Instruction stream, Single Data stream (MISD), Single Instruction stream, Multiple Data stream (SIMD), Multiple Instruction stream, Multiple Data stream (MIMD)[8]. We now don’t want to examine each of these classes in some detail. But it is necessary investigate the details of shared memory structure that is the base of message passing programming method. In third class, a parallel computer consists of N identical processors, as shown in Fig.1. Each of the N processors possesses its own local memory where it can store both programs and data. All processors operate under the control of a single instruction stream issued by a central control unit. Equivalently, the N processors may be assumed to hold identical copies of a single program, each processor's copy being stored in its local memory. There are N data streams, one per processor. The processors operate synchronously: At each step, all processors execute the same instruction, each on a different datum. The instruction could be a simple one (such as adding or comparing two numbers) or a complex one (such as merging two lists of numbers). Similarly, the datum may be simple (one number) or complex (several numbers). Sometimes, it may be necessary to have only a subset of the processors which execute an instruction. This information can be encoded in the instruction itself, thereby telling a processor whether it should be active (and execute the instruction) or inactive (and wait for the next instruction). There is a mechanism, such as a global clock, that ensures lock-step operation. Thus processors that are inactive during an instruction or those that complete execution of the instruction before others may stay idle until the next instruction is issued. The time interval between two instructions may be fixed or may depend on the instruction being executed. In most interesting problems that we wish to solve on an SIMD computer, it is desirable for the processors to be able to communicate among themselves during the computation in order to exchange data or intermediate results. This can be achieved in two ways, giving rise to two subclasses: SIMD computers where communication is through a shared memory and those where it is done via an interconnection network. An example of a SIMD computer shown below in figure 1:

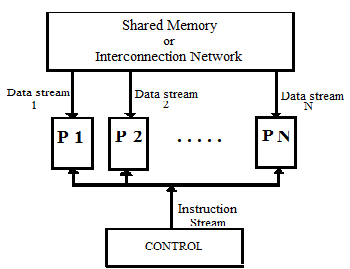Figure 1. A SIMD computer

Shared-Memory (SM) SIMD Computers: This class is also known in the literature as the Parallel Random-Access Machine (PRAM) model. Here, the N processors share a common memory that they use in the same way a group of people may use a bulletin board. When two processors wish to communicate, they do so through the shared memory. Say processor “i” wishes to pass a number to processor “j”. This is done in two steps. First, processor “i” writes the number in the shared memory at a given location known to processor “j”. Then, processor “j” reads the number from that location. During the execution of a parallel algorithm, the N processors gain access to the shared memory for reading input data, for reading or writing intermediate results, and for writing final results. The basic model allows all processors to gain access to the shared memory simultaneously if the memory locations they are trying to read from or write into are different. However, the class of shared-memory SIMD computers can be further divided into four subclasses, according to whether two or more processors can gain access to the same memory location simultaneously:

(i) Exclusive-Read, Exclusive-Write (EREW) SM SIMD Computers. Access to memory locations is exclusive. In other words, no two processors are allowed simultaneously to read from or write into the same memory location.

(ii) Concurrent-Read, Exclusive-Write (CREW) SM SIMD Computers. Multiple processors are allowed to read from the same memory location but the right to write is still exclusive: No two processors are allowed to write into the same location simultaneously.

(iii) Exclusive-Read, Concurrent-Write (ERCW) SM SIMD Computers. Multiple processors are allowed to write into the same memory location but read accesses remain exclusive.

(iv) Concurrent-Read, Concurrent-Write (CRCW) SM SIMD Computers. Both multiple-read and multiple-write privileges are granted. Allowing multiple-read accesses to the same address in memory should in principle pose no problems (except perhaps some technological ones not to be discussed here). Conceptually, each of the several processors reading from that location makes a copy of the location's contents and stores it in its own local memory. With multiple-write accesses, however, difficulties arise. If several processors are attempting simultaneously to store (potentially different) data at a given address, which of them should succeed? In other words, there should be a deterministic way of specifying the contents of that address after the write operation. Several policies have been proposed to resolve such write conflicts, thus further subdividing classes (iii) and (iv). Some of these policies are:

(a) the smallest-numbered processor is allowed to write, and access is denied to all other processors;

(b) all processors are allowed to write provided that the quantities they are attempting to store are equal, otherwise access is denied to all processors;

(c) the sum of all quantities that the processors are attempting to write is stored[9].

Here, there is a very important moment that we should not disregard it. A fundamental problem in distributed computing is performing N tasks in a distributed system consisting of P processors, and despite the presence of failures and delays. The abstract problem is called Do-All when processors communicate by exchanging messages and the tasks are similar in size and independent. Examples of such tasks include searching a collection of data, applying a function to the elements of a matrix, copying a large array, or solving a partial differential equation by applying shifting method. This problem has been studied in different settings [10, 11], including some notable work in message-passing models[12-14], partitionable networks[15-17], and shared-memory models[18-21], where the problem is called Write-All. Depending on the model of computation, algorithmic efficiency is evaluated in terms of time, work, and message complexity. Work is defined as either the total number of steps taken by the available processors[22], or the total number of tasks performed[23]. Message complexity is expressed as the total number of point-to-point messages.

4. Feasibility of the Shared Memory Model

The SM SIMD computer is a fairly powerful model of computation, even in its weakest manifestation, the EREW subclass. Indeed, the model allows all available processors to gain access to the shared memory simultaneously. It is sometimes said that the model is unrealistic and no parallel computer based on that model can be built. The argument goes as follows. When one processor needs to gain access to a datum in memory, some circuitry is needed to create a path from that processor to the location in memory holding that datum. The cost of such circuitry is usually expressed as the number of logical gates required to decode the address provided by the processor. If the memory consists of M locations, then the cost of the decoding circuitry may be expressed as f(M) for some cost function f If N processors share that memory as in the SM SIMD model, then the cost of the decoding circuitry climbs to N x f(M). For large N and M this may lead to prohibitively large and expensive decoding circuitry between the processors and the memory. There are many ways to mitigate this difficulty. All approaches inevitably lead to models weaker than the SM SIMD computer. Of course, any algorithm for the latter may be simulated on a weaker model at the cost of more space and/or computational steps. By contrast, any algorithm for a weaker model runs on the SM SIMD machine at no additional cost. One way to reduce the cost of the decoding circuitry is to divide the shared memory into R blocks, say, of MIR locations each. There are N + R two-way lines that allow any processor to gain access to any memory block at any time. However, no more than one processor can read from or write into a block simultaneously. the i-th processor wishes to gain access to the j-th memory block, it sends its request along the i-th horizontal line to the j-th switch, which then routes it down the j-th vertical line to the j-th memory block. Each memory block possesses one decoder circuit to determine which of the M/R locations is needed. Therefore, the total cost of decoding circuitry is R x f(M/R). To this we must add of course the cost of the N x R switches.

5. Conclusions

This paper presents an introduction to the shared memory architecture of parallel computers and especially the method of message passing that based on this architecture. Here we investigated details of this type and analyzed characteristics and superiorities of this method. Shared-memory model and the message-passing model are the major aspects of distributed computing problem. In the first model, we typically assume that the processes are connected through reliable communication channels, which do not lose, create or alter messages. Processes communicate using send and receive primitives, which encapsulate TCP-like communication protocols provided in modern networks. But the second model abstracts a hardware shared memory made of registers. The processes exchange information using read and write operations exported by the registers and processors communicate by writing and reading to share registers. In the message-passing model, n processors are located at the nodes of a network and communicate by sending messages over communication links. This task is somewhat easier in shared-memory systems, where processors enjoy a more global view of the system. There are many applied and computational problems in every field of sciences such as mathematics and engineering which can be resolve by parallel algorithms and especially by the techniques containing message passing programming methods, of course according to their characteristics. Such emulation is very appealing because it is usually considered more convenient to write distributed programs using a shared memory model than using message passing, and many algorithms have been devised assuming a hardware shared memory[24]. Our approach is to study emulation of shared-memory algorithms for performing tasks in asynchronous message-passing systems. Our goal is to resolve different and actual applied and computational problems in various fields to improve their complexity compared with their non parallel algorithms. At the next researches we want to focus on the applying of parallel algorithms and specially using message passing structure for the computational problems related optimization of mathematical difficulties[25-27]. We will investigate applying mentioned parallel algorithm at the field of oil extraction problem to save the large amount of time spending for solving them[27-29].

ACKNOWLEDGEMENTS

We are heartily thankful to our supervisor, prof. F. Aliev and whose encouragement, guidance and support from the initial to the final level enabled us to develop an understanding of the subject. Special appreciation to our parents for supporting us in different levels of life and education. Many thanks to Baku State University and deeply specially to Islamic Azad University of Ahar branch for inseparable supports.