Advances in Computing

p-ISSN: 2163-2944    e-ISSN: 2163-2979

2012;  2(4): 54-59

doi: 10.5923/j.ac.20120204.02

Using Maekawa’s Algorithm to Perform Distributed Mutual Exclusion in Quorums

Ousmane Thiare 1, Papa Alioune Fall 2

1Department of Computer science, Gaston Berger University, BP 234 Saint-Louis, Senegal

2Department of Applied Physics, Gaston Berger University, BP 234 Saint-Louis, Senegal

Correspondence to: Ousmane Thiare , Department of Computer science, Gaston Berger University, BP 234 Saint-Louis, Senegal.

Email:

Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.

Abstract

In distributed systems,cooperating process essh are both local and remoter sources. Chance is very high that multiple processes makesimultaneous requests to the same resource. If the resourcerequires mutually exclusive access (critical section - CS), then some regulation is needed to access it for ensuring synchronizedaccess of the resources thatonly one process could use the resource at a given time. This is the distributed mutual exclusion problem. The problem of coordinating the execution of critical sections by eachprocessissolved by providing mutually exclusive access to the CS. Mutual exclusion ensures that concurrent processes make a serialized access to shared resources.Quorum-based algorithms offer the advantage of protocol symmetry, spreading effort and responsibility uniformly across the distributed systems. In thispaper, we have proposed a permission baseddistributedmutual exclusion algorithmwhichis an improvement of Maekawa’s algorithm. The number of messages required by the improvisedalgorithmis in the range 3Mto 5Mper critical section invocation whereMis the number of intersection nodes1 in the system. A reduction in number of message by restricting the communication of anynodewith the intersection nodes of the quorums, withoutany modification of the basic structure of the algorithm.

Keywords: Mutual Exclusion, Communication, Quorum

Article Outline

1. Introduction
2. Related Work
3. Distributed System Model
    3.1. Notion of Quorum
4. Maekawa’s Algorithm
    4.1. The Computational Model
    4.2. The Algorithm
5. The Proposed Algorithm
6. Proof of Correctness
    6.1. Mutual Exclusion
    6.2. Deadlock and Starvation
7. Performance Analysis
8. Conclusions

1. Introduction

Distributed mutual exclusion problem arise when concurrent access to protected resource (termed as Critical Section (CS)) by several sites is involved. In distributed mutual exclusion, the requirement is to serialize the access to CS in the absence of shared memory, which further complicates the problem.
Mutual exclusion (MUTEX) is a fundamental problem in distributed systems, where a group of hosts intermittently require entering the Critical Section in order to exclusively perform some critical operations, e.g. accessing the shared resource. A solution to the MUTEX problem must satisfy the following three correctness properties:
• Mutual Exclusion (safety): At most one host can be in the CS at any time;
• Deadlock Free (liveness): If any host is waiting for the CS, then in a finite time some host enters the CS;
• Starvation Free (fairness): If a host is waiting for the CS, then in a finite time the host enters the CS.Many MUTEX algorithms have been proposed for traditional distributed systems[2] which can be categorized into two classes: token-based algorithms and permission-based algorithm. In token-based algorithms, a token is passed among all the hosts. A host is allowed to enter the CS only if it possesses the token. In a permission-based algorithms, the host requesting for the CS must first obtain the permissions from other hosts by exchanging messages.
Distributed mutual exclusion algorithms can be classified as token-based and non-token-based as suggested by[2], or as token-based and permission-based as suggested by[3]. In this paper, we proposed a permission based distributed mutual exclusion algorithm, which is an improvement of Maekawa’s algorithm[1].
In Suzuki-Kasami’s broadcast[14], when a node wants to enter the critical section, it broadcasts a message to all other nodes. Whoever holds the token sends the token directly to the node tat wants to enter the CS. The algorithm requires N messages for handling each request. The simplest of token-based algorithms is the Agrawal-Elabbaei’s token ring approach[13]. In this algorithm, the nodes in the system form a logical ring. A token always passes around the ring clockwise or anticlockwise. A node can enter the critical section if it holds the token. On an average N/2 messages are required to handle one request in an N nodes system.
Niealsen and Mizuno extended by passing the token directly to the requesting node instead of through intermediate node[15]. Naimi-Trehel’s algorithm[16] maintains a dynamic logical tree, such that the root of the tree is always the last node that will get the token among the current requesting ones. Chang, Singhal and Liu[17] improved this algorithm, aimed to reduce the number of messages to find the last requesting host in the logical tree. Mueller[18] also proposed an extension to Naimi-Trehel’s algorithm, introducing the concept of priority and the algorithm satisfies the request with higher priority.
Garcia-Molina and Barbara[4] first introduced the concept of coterie which could be mainly used to devise permission based distributed mutual exclusion algorithms. A coterie consists of collection of sets of sites in the system and these sets are called quorums. In general, when a node wants to execute its CS, it has to obtain permission from processes of any quorum in the coterie. Maekawa’s algorithm[1] was the first coterie-based algorithm where the nodes of the system are logically arranged into groups. Any node intending to execute its CS has to obtain permission from all the nodes in its respective group and these groups were created such that any two groups had at least one node in common (referred to as intersection nodes) which act as arbitrators. In this paper, we further restrict the communication of the processes, which want to execute its CS to their intersection nodes and achieve distributed mutual exclusion in lesser number of messages.
Maekawa’s algorithm[1] uses cK messages to create mutual exclusion in the distributed system, whereas our proposed algorithm takes cM (M) messages per CS invocation where M, K and c are integers and 3 ≤ c ≤ 5. However, our proposed algorithm preserves all the advantages of Maekawa’s algorithm[1] and remains similar to it. The algorithm proposed in this paper is not fair, the synchronization delay is 2 and the algorithm is starvation-free.
The problem of resolving conflicting access to resources also arise in replicated databases, where the emphasis is on resolving read and write conflicts efficiently. Many methods[5-8,10,12] have been used to address this issue.
Document structure: The rest of the paper is organized as follows. Section 2. is designated for related work. Section 3. Talk about our distributed system model. Section4. reviews Maekawa’s algorithm[1]. In section5, we present our proposed algorithm. Section6. presents the proof of correctness. In section 6, we present the analysis of the proposed algorithm. Finally, we conclude in section 8.

2. Related Work

Quorum systems are used to solve many coordination problems in distributed systems such as mutual exclusion, data replication, distributed consensus, and commits protocols.
A quorum system is a collection of sets quorums, which mutually intersect. A replicated database is a distributed database in which multiple copies of some data items are stored at multiple servers. One of the advantages of data replication is to increase data availability so that the system can remain operational even though some servers have failed. Another advantage of data replication is to improve performance. With many copies of each data item being available, a user transaction is more likely to find the data is needed nearby. However, these benefits are offset by the cost of maintaining data consistency.
The load of a quorum system measures the share that processors have handling request to quorum. Given a probability distribution on quorum accesses, the load of an element is equal to the sum of the access probability of all quorums it belong to. For a given probability distribution, the quorum system load is the maximum of the load of all elements. The load of a quorum system is the minimum over all access probability distributions.The availability of a quorum system measures the probability that the system is usable when failures occur. A quorum system is available given that processors fail according to some probability distribution. The failure probability of a quorum system is the probability that the quorum is not available.
The cost failure is used to measure the overhead message complexity due to failures. If a quorum set has some faulty servers, then it is not usable because it is not guaranteed to share a correct server with every other quorum. In this case, a server attempting to access the quorum with failed servers must find another quorum with no failed servers. Informally, the cost of failures is the additional number of servers that need to be contacted when failure occurs.
Kumar introduced quorum system based on a hierarchical construction Maekawa showed that for a fixed integer k, the maximum possible value of N in which all the properties can be satisfied is equal to k(k+1)+1, where k is a power prime, by assuming that any two quorums have only one intersection. Hence, the theoretical lower bound of the quorum is approximately equal to √N. Furthermore, he also mentioned that finding the possible solution for N=k(k+1)+1 is equivalent to find a finite projective plane of order k. Nevertheless, not all finite projective planes exist and we only know how to construct those with power order k=pi where p is a prime number and i an integer.
For the others values of k, one way to create the sets is relaxing some of the conditions imposed on the quorums, or by creating sets for a larger N and the discarding some sets. In theory, we can solve the optimal quorum problem by generating all the combinations and see which one satisfies all properties. However, the time complexity of this exhaustive search algorithm is exponential.
To solve this problem, several methods have been proposed to generate the near-optimal solution.

3. Distributed System Model

The distributed system consists of n distinct servers, which communicate with each other by message passing over connected network. The messages take finite but arbitrary time to reach at the receiving servers. In this paper, we share in their design to following assumptions and conditions for the distributed system environment. All processes in the distributed system are assigned unique identification numbers.

3.1. Notion of Quorum

Definition 3.1:A finite projective plane is a collection of k2+k+1 points and k2+k+1 lines such that the following fours axioms hold:
(ⅰ) Every line contains k+1 points.
(ⅱ) Every point lies on k+1 lines.
(ⅲ) Any two distinct lines intersect in exactly one point.
(ⅳ) Any two distinct points lie exactly one line.
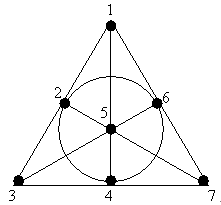Figure 1. The finite projective plane of order 2 (Fano plane)
From the Figure 1., we can determine the following sets of 7 lines. Any two lines intersect in one point, and any two points lie one line.
S1={1, 2, 3}, S2={2, 5, 7}, S3={3, 4, 7}, S4={4, 1, 5}, S5={5, 3, 6}, S6={6, 2, 4}, S7={7, 1, 6}.
Definition 3.2:A quorum systems Q over a set S, is a set of subsets of S such that any two distinct subsets intersect.
Definition 3.3:Give a set S={1, 2, 3, …, n} representing the servers of network, find n=S subsets Si⊆S such that the following properties are satisfied:
(ⅰ) Intersection property:
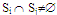(ⅱ) Minimality:
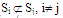(ⅲ) Equal size:Si=k+1
(ⅳ) Equal effort: every server i appears in (k+1) Sj
The subsets Sis are called quorum. Quorum that satisfy the minimality, the mutual intersection and non-emptiness properties from a coterie. The equal size and equal effort properties define the additional notion of symmetry in the coterie. Equal size quorum ensures that each server or client sends the same number of message to request the shared resource. The equal effort property requires that each server be included in the same number of quorums, ensuring that all sites expend the same effort in enforcing distributed mutual exclusion.
The selection of Sis is not unique. There exists a number of ways to select a set Si that satisfies the above properties.The problem of finding a set of Q is that satisfies these conditions are equivalent to finding a finite projective plane of N points. It is known that there exists a finite projective plane of order k if k is a power of a prime number p. This finite projective plane has (k+1) lines and k points per line.

4. Maekawa’s Algorithm

In this section, we present the computational model for the proposed algorithm and a review of Maekawa’s algorithm.

4.1. The Computational Model

In this paper, we assume that a distributed system, which is common to Maekawa’s algorithm and to the proposed algorithm, consists of N sites {1, 2, 3, …, j, …, N}. A distributed system is asynchronous, i.e., there is no common global clock. Information exchanged between processes is done by asynchronous message passing. Each communication channel is FIFO and each message sent is delivered within finite time, but there is no upper bound on message delivery time. We assume that the system is error free.
The different type of messages used is REQUEST, LOCKED, INQUIRY, FAILED, RELINQUISH and RELEASE. Timestamps (TS) at any site i (where 1≤ i ≤ N), TSi are ordered by (Li, i), containing the Lamport’s logical clock[10] value Li and the site id i.
An ordering, “<” on timestamps is defined as:
TSijiff (Li j) or (Li=Lj and i < j).

4.2. The Algorithm

In Maekawa’s algorithm, a site does not request permission from all the sites, but only from a subset of sites. The sites of the system are divided into groups called quorums (Si,,1≤ i ≤ N). The quorums are constructed such as to satisfy the following conditions:
(ⅰ) ∀i, ∀j, Si ∩ 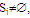i ≠ j, 1≤i,j≤N
(ⅱ) ∀i, node i ∈Sj, 1≤ i ≤N
(ⅲ) ∀i, Si=K, 1≤ i ≤ N
(ⅳ) ∀j, node j is with in KSis, 1≤i,j≤N
Condition (i) (non null intersection property) is a necessary condition for the Si’s so that mutual exclusion requests can be resolved. Condition (ii) reduces the number of messages to be sent and received by a node. Condition (iii) means that each node needs to send and receive the same number of messages to obtain mutual exclusion (equal work). Finally condition (iv) signifies that each node is equally responsible for mutual exclusion (equal responsibility).
For example, the finite projective plane of order 2 seen in Section 3. workswell in the case of Maekawa's algorithmwith the properties of quorums definedabove.
Maekawa establishes the following relationship between N and K: N=K(K-1)+1. Hence K can be found approximated to √N.
For any node i, who intends to execute its CS, the algorithm works as follows.
Entry section:Process i multicasts the REQUEST to all the nodes in its Si including itself. The intersection nodes can send the REQUEST messages to any one of the districts to which theybelong. When a process j receives the REQUEST message, it sends LOCKED message to site i if it has not yet sent it to any other site from the time it received RELEASE message. Or else it queues the REQUEST.
CS execution: Process i executes its CS after receiving LOCKED message from all the nodes of its Si.
Exit section: After executing its CS, site i sends RELEASE message to all nodes of its Si which restores node’s right to send LOCKED message to any other pending requests in the queue.
This basic algorithm is prone to deadlock which is handled as follow: Assume that a site j has LOCKED message to some site k and it later receives a REQUEST message from any other site i (i≠ k). Then, node j sends FAILED message to site i if TSki, otherwise it sends INQUIRY message to site k. When such a process k receives INQUIRY message, it sends RELINQUISH message to site j if site k has received FAILED message from at least one site in Sk, and has not received new LOCKED message from it(after receipt of FAILED message).

5. The Proposed Algorithm

Our proposed algorithm presents an improvement to the Maekawa’s distributed mutual exclusion algorithm. From Maekawa’s algorithm[1] it is clear that the role of the arbitrator is to resolve the conflicting requests to enter CS. Every node has the responsibility to become an arbitrator to handle the conflicting requests coming from the quorum to which it belongs. Nodes that belong to more than one quorum (referred to as intersection nodes), act as inter-quorum arbitrators, resolving conflicting requests arising from nodes of different quorums. Because of the role played by these intra and inter-quorum arbitrator, the mutual exclusion condition is maintained throughout the entire network.
Intersection nodes can also act as intra-quorum arbitrators since they are also the members of the quorum. Here we see that, since the intersection nodes can act as both inter-quorum and intra-quorum arbitrators, and since every quorum should have at least one intersection node, all conflicting requests can be resolved by communicating with intersection nodes of the system. This way, we can achieve per CS invocation with respect to Maekawa’s algorithm[1], as all the messages required to communicate with non-intersection nodes can be eliminated.
Hence our proposition is: Maekawa’s distributed mutual exclusion algorithm can perform better (in terms of number of messages required) by restricting the entire algorithm related communication to be carried out with only the intersection node in the quorum.
In Maekawa’s algorithm[1], all nodes in the quorum are intersection nodes (from condition (iv) for construction of quorums which is outlined in section 4.) and hence all nodes work as inter-quorum arbitrators. To ensure that number of nodes in the quorum, we propose to liberalize the conditions for construction of quorums in Maekawa’s algorithm[1].
The quorums in our algorithm are constructed using the following conditions:
(i) ∀i, ∀j, Si ∩ 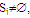i ≠ j, 1≤i,j≤ y, where y is the number of quorums, y ≤ N
(ii) Node i belongs to at least one of the quorums
(iii) The number of nodes in the quorum needs to be equal.
Here, we presented the conditions in the same way as done by Maekawa’s algorithm in the previous section so that the reader may note the difference. Conditions (i) and (ii) are required to ensure correctness of the algorithm. In Maekawa’s algorithm[1], it was required to have k number of nodes in the entire quorum to ensure that all nodes perform an equal amount of work for each CS invocation, which is a desirable feature of a truly distributed system. The system using our algorithm would be a pseudo-distributed system as the non-intersection nodes do not participate in CS invocation of other nodes and hence condition (iii) follows.
The basic working of the algorithm and the required types of messages need not to be modified. This improvisation would shift the responsibility to maintain the mutual exclusion condition to the intersection nodes.

6. Proof of Correctness

6.1. Mutual Exclusion

Mutual exclusion is achieved when no pair of processes is ever simultaneously in its critical section. For any pair of processes, one must leave its CS before the other may enter.
Theorem 6.1: The proposed algorithm ensures the mutual exclusion property.
Proof: By contradiction. Let us assume that, any two nodes i and j are executing the CS simultaneously. Let Si and Sj be the quorums of i and j respectively. Let Si’ and Sj’ be sets of intersection nodes of Si and Sj respectively. Let k be a node that belongs to the intersection of Si and Sj.
Consider the case when Si=Sj (i.e. i and j belongs to the same quorums), then, we choose k from Si’. Since Si=Sj, we have Si’=Sj’. Thus k belong to Sj’, hence k belongs to both Si’ and Sj’. If Si≠Sj, since k belongs to both Si and Sj, k is an intersection node, k belongs to both Si’ and Sj’.
Since i is executing the CS, i has captured the LOCKED message from the entire node belonging to Si’ including k. Since j is also executing the CS, j also should have captured the LOCKED messages from all the nodes belonging to Sj’ including k. Thus k has been locked by 2 requests simultaneously. However, according to the algorithm only one request can lock a node at a time. Thus maximum of only one process can execute the CS at any time.
This proof holds well when i and j belong to same quorum as well as different quorums. Thus, we see that the proposed improvement does not affect the correctness of the algorithm.

6.2. Deadlock and Starvation

The system of nodes is said to be deadlocked when no process is in its CS and no requesting process can ever proceed to its CS.
Starvation occurs when one process must wait indefinitely to enter its CS even though other processes are entering and exiting their own critical section.
Theorem 6.2: The proposed algorithm is deadlock and starvation free.
Proof: Since no two requests carry same timestamp (priority), total ordering is achieved among requests. If the total ordering condition is followed strictly “circular wait” condition is not satisfied, and hence deadlock cannot occurs[11].
If an arbitrator (here an intersection node) finds out that it has actually violated the total ordering condition by sending LOCKED message to a request with higher priority when there is a request with lower priority waiting in the request queue, it sends an INQUIRY message to the recipient of the LOCKED message. Then if the recipient node has already started executing the CS, it will not reply. If the recipient node has not yet entered the CS and if it receives a FAILED message from at least one of the intersection process, then it would send the RELINQUISH message to the arbitrator and release the lock on that node. Then the arbitrator can get locked to the request with lesser timestamp. Here the “No pre-emption” condition is not satisfied. Thus, in any case a deadlock situation cannot occur in the system.
Since no modification has been done to the way the timestamp of a node is used or updated, even the improvised algorithm is starvation free, similar to the original Maekawa’s algorithm[1].

7. Performance Analysis

Let M be the number of intersection nodes in the quorum. In the best case where there is no relinquishment happening, we have M REQUEST messages being sent by the requesting node for every CS invocation. The node receives M LOCKED messages. After executing its CS, node sends M RELEASE messages. Thus 3M number of message is required. In the worst case, where every LOCKED message is relinquished, we have additional k number of INQUIRY and RELINQUISH messages each. Thus 5M (3M+2M) number of messages is required. Hence, the number of messages required for every CS execution after modification is cM, where 3≤ c≤5.
The value of M depends on the way the have the nodes have been distributed into various quorums. When M=1, then the system is similar to a centralized system. When M = N, for all the nodes, then the algorithms performs similar to that of Ricart-Agrawala’s algorithm[12]. WhenM=√N, the algorithm performs similar to original Maekawa’s algorithm. Also, it can be noted that, in any case, the number of intersection processes in a quorum is lesser than or equal to the number of messages required by the original algorithm. The system can be designated is such a way that M <√N for all the quorums of the system, in which case the improvised algorithm would require lesser number of messages than the original Maekawa’s algorithm.

8. Conclusions

In this paper, we have proposed a permission-based distributed mutual exclusion algorithm, which is an improvement of Maekawa’s algorithm. The proposed algorithm is a modification of Maekawa’s distributed mutual exclusion algorithm and signification reduction in the number of messages is being achieved by restricting the communication of any node of the quorums. The proposed algorithm does not introduce any additional overheads over the existing Maekawa’s algorithm, which requires 3K to 5Knumbers of messages per CS invocation, where K is the number of nodes in the quorum (M < K).

References

[1]  M. Maekawa, “A √Nalgorithm for mutual exclusion in decentralized systems”, ACM Transactions in Computer Systems, vol. 3., no. 2., pp. 145-159, 1985.
[2]  M. Singhal, “A taxonomy of distributed mutual exclusion”, Journal of Parallel and Distributed Computing, vol. 18., pp. 145-159, 1993.
[3]  M. Raynal, “ A simple taxonomy for distributed mutual exclusion algorithms”, ACM Operating Systems Review, vol. 23., no. 2., pp. 47-51, 1991.
[4]  H. Garcia-Molina, D. Barbara, “How to assign votes in a distributed system”, Journal for the Association for Computing Machinery”, vol. 32., no. 4, pp. 841-860, 1985.
[5]  M. Wiesmann, F. Pedone, A. Schiper, B. Kemme, G. Alonso, “Understanding replication in databases and distributed sytems” ICDCS Proceedings, pp. 464-474, 2000.
[6]  V.S. Ananthanarayana, K. Vidyasankar, “Dynamic primary copy with piggy-backing mechanism for replicated UDDI registry”, ICDIT, LNCS, vol. 4317, Springer, pp. 389-402, 2006.
[7]  A.R. Bharath Kumar, B.U Pradhan, V.S. Ananthanarayana, “An efficient Lazy dynamic primary copy algorithm for replicated UDDI registry”, Proceedings of ICCNS, pp. 161-166, 2008.
[8]  B.U. Pradhan, A.R. Bharath Kumar, V.S. Ananthanarayana, “An efficient eager dynamic primary copy algorithm for distributed databases”, ICDCN, LNCS, 2009.
[9]  B.U. Pradhan, A.R. Bharath Kumar, V.S. Ananthanarayana, “A tree based dynamic primary copy algorithm for distributed databases” proceedings of ICIP, pp. 564-571, 2008.
[10]  L. Lamport, “Time, clock and the ordering of events in a distributed system”, Communications of the ACM, pp. 558-565, 1978.
[11]  E.G. Cuffman, J.M. Elphick, A. Shoshani, “System deadlocks”, ACM Computing Surveys, pp. 66-78, 1971.
[12]  G.Ricart, “An optimal algorithm for mutual exclusion in computer networks”, Communications of the ACM, vol. 24., no. 1, pp. 9-17, 1981.
[13]  D. Agrawal, A. Elabbaei, “An efficient fault-tolerant solution for distributed mutual exclusion”, ACM Transactions on Computer Systems, vol. 9, no. 1, pp. 1-20, 1991.
[14]  I. Suzuki, T. Kasami, “A distributed mutual exclusion”, ACM Transactions on Computer Systems, vol. 3, no. 4, pp. 344-349, 1985.
[15]  M. Naimi, M. Trehel, A. Arnold, “A log(N) distributed mutual exclusion algorithm based on path reversal”, Journal of Parallel and Distributed Computing, vol. 34, no. 1, pp. 1-13, 1996.
[16]  I. Chang, M. Singhal, M.T. Liu, “An improved log(N) mutual exclusion algorithm for distributed systems”, Proc. of the International Conference on Parallel and Distributed Processing, pp. 295-302, 1990.
[17]  F. Mueller, “Prioritized token-based mutual exclusion for distributed systems”, Proc. of the 12th Symposium of Parallel and Distributed Processing, pp. 791-795, 1998.
[18]  F. Kawsar, H.S. Shariful, M.A. Razzaque, M.A. Mottalib, “An efficient token based algorithm for mutual exclusion in distributed system, Journal of Engineering and technology, vol. 2, no. 2, pp. 39-44, 2003.