1. Introduction

Watermarking[1, 16] is a very essential solution for copyright protection of different multimedia contents. This method wisely hides some useful information in the efficient part of the original content. Unlike to cryptography, the digital watermarking technique is able to protect digital works (assets) after the transmission phase and the legal access. Watermarking algorithms are classified into non-blind and blind watermarking schemes depending on whether or not the original digital work is needed at extraction phase.

Watermark robustness is the ability to recover the watermark even if the watermarked 3D model has been manipulated. Usually, one hopes to construct a robust watermark which is able to go through common malicious attacks for copyright protection purposes. However, sometimes the watermark is intentionally designed to be fragile, even to very slight modifications, in order to be used in authentication applications.

According to the insertion area watermarking algorithms are divided into two categories, spatial domain method or transform domain method. Spatial domain method embeds the watermark by directly modifying the original image data (pixel value), while in the frequency domain method; a watermark is embedded into coefficients by modifying it after taking the transform such as Discrete Cosine Transform(DCT), Fourier transforms (FFT) and wavelet transforms (WT). Spatial domain methods as described in the papers[2, 3] works fast but are not robust to attacks. Paper[4] also presented different spatial and spectral domain algorithms for 3d model watermarking. In other hand transform domain methods[5] are robust and widely used methods due to various characteristics (for ex. MRR etc.) available in it. Papers[6, 7] presented a blind watermarking multi-resolution decomposition and reconstruction algorithms for 3D irregular meshes. Paper[8] represented a novel blind watermarking algorithm based on a joint DWT-DCT for 2d digital image. He exploited strength of two common frequency domain methods; DCT and DWT, to obtain imperceptibility and robustness. The idea of inserting watermark in the combined transform was based on the fact that, the jointed transform can eliminate the drawback of each other and then, an effective watermark is embedded in the most robust and imperceptible parts of the image. Watermarking is done with embedding the watermark in the special middle frequency coefficient sets of 3-levels DWT transformed of a host image, followed by computing 4×4 block-based DCT on the selected DWT coefficient sets.

Newly certain watermarking algorithms have been developed which makes use of neural networks. Paper[9] presented a robust and novel idea to insert a watermark into a digital video based on 3D DWT and Artificial Neural Network (ANN). Watermark is inserted into the selected wavelet coefficients based on the association between the coefficient and its neighbours’ std. deviation. Paper[10] also uses Artificial Neural Network concept to develop image watermarking algorithm. Paper[11] inserts watermark in digital media to find the owner of the content using ANN. A watermark is embedded in the coordinates of vertices without perceptible distortion. ANN classifier is used to select the vertices for watermark insertion. Paper[12] presented a novel watermarking algorithm for 3D triangular meshes using neural networks. A watermark is embedded in the vertices having different valences. A feed-forward back-propagation neural network is used for selecting the vertices for watermark insertion. Paper[16] provides a fragile watermarking technique to watermark 3D surface models into other 3D surface models using wavelets and DCT. The watermark is extracted using blind method.

The algorithm proposed in this paper embeds the watermark by modifying the wavelet (medium frequency) coefficients of the 3D model at third level based on ANFIS, Adaptive Neuro fuzzy inference system. Hybrid method is used to train the ANFIS model. Watermark can be extracted in the presence of original 3D model and watermarked model. Thus enhancing the robustness and making it more imperceptible as compared with other existing algorithms. More attention would be paid to ensure that the embedding algorithm preserves the visual integrity of the models.

2. Background

Wavelets: Wavelets[13] has time as well as scale aspects. These aspects are useful for various applications like: image simplification, in oceanography, in earth studies, fingerprinting, medicine etc. Some of the important characteristics of the wavelets are:

● It provides local analysis of a signal.

● It provides windowing techniques with different sizes.

● It permits variable time intervals (longer or smaller) for low and high frequency information.

● It also provides new aspects which are not available with other signal analysis techniques, for ex. breakdown points, discontinuities in higher derivatives and self-similarity.

● It can even compress or de-noise a signal without disturbing visual quality of a signal.

Wavelet analysis[13] process divides the signal into two components: approximation and detail. Approximation and detail components are also called as low frequency and high frequency components resp. The decomposition of a signal into low and high frequency components is also called as analysis. The reconstruction of these components back into the original signal without loss of information is called synthesis. In Matlab decomposition process is performed by DWT function and the reconstruction process is performed by IDWT function.

Multi-resolution analysis[14] is a useful tool to reach an acceptable trade-off between the mesh complexity and the capacity of the available resources. Such an analysis produces a coarse mesh which represents the basic shape (low frequencies) and a set of details information at different resolution levels (median and high frequencies). These methods also allow realizing a synthesis process during which multiple representations with different complexities can be created.

The most interesting point of multi-resolution analysis for watermarking is its flexibility. There are different available locations allowing meeting different application demands. For example, insertion in the coarsest mesh ensures a good robustness, while embedding in the details parts provides an excellent capacity. The insertion in low resolution can be both more robust and more imperceptible thanks to a dilution effect. The insertion in high resolution level may permit to construct some effective fragile watermarks with a precise localization ability of the attacks.

Wavelets are a common tool for such a multi-resolution analysis. The watermark can be inserted either in the coarsest mesh, or in the wavelet coefficients at different levels. In fact, these wavelet coefficients are 3D vectors associated with each edge of the corresponding coarser mesh.

ANFIS: Previously[13] the basic configuration of the Fuzzy Inference System (FIS) converts the input values into the input membership functions (MFs), input MFs to rules, rules to a set of output values, output values to output MFs and the output MFs to a particular output value or some decision parameter. Dissimilarities between the input values can be described by using the neuro-adaptive learning techniques of the ANFIS function provided by MATLAB fuzzy logic toolbox. Working of ANFIS function is equivalent to the working of neural networks. ANFIS have following characteristics:

● Creation, training and testing facilities for a model.

● A method to learn information about a data set.

● Calculation of the MFs parameters that is suitable for input/output data, either by using back propagation or in combination with a least squares type method called as hybrid method.

● Training to the FIS model by changing the MFs parameters in accordance with the error value.

● Testing of model against training as well as testing data.

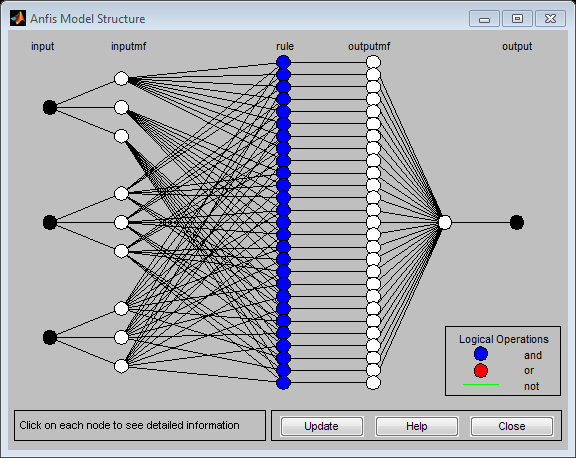Figure 1. ANFIS Model Structure[13] for Hybrid Method

Epoch or error values are used to discontinue the training to ANFIS. That is the training is stopped if the epoch value reaches to its maximum value or if the training error objective is accomplished. After the successful completion of training of FIS model it can be authenticated by testing it against training or testing data. ANFIS only supports Sugeno Type Systems () with following characteristics:

● STS used should be either zeroth order or first order.

● Has single output.

● Have no rule sharing.

● All rules should have same weight value.

ANFIS model for 3 inputs and 1 output value is shown in the figure1. It has 3 MFs for each input and 27 rules & MFs for output.

3. Watermark Insertion Algorithm

Following assumptions are made before applying the actual algorithm:

● Trndata is a file used to store the training data which contains desired input and output values. This file is arranged as an array of four column vectors. First three column vectors are used to store input values and last column vector is used to store output values. Here input contains information about features of 3D models. And output contains corresponding Weight factor.

● Testdata is a file used to store testing data values. Structure of the file is same as training data file.

● N = number of 3D models for training.

● M = number of 3D models for testing.

● Number of membership functions for each input=3.

● Number of membership functions for output=27.

● Number of training epochs at initial level = 10. (We can increase this number to reduce error value in training).

● Error tolerance=0.

● Number of rules=27.

● Training method=Hybrid

Step 1: Preparation of 3D models for training, testing and for watermark.

Step 2: Extraction of features of 3D models for training.

For i = 1 to N

a) Apply Haar wavelet transform to the i^th model prepared for training and generate four coefficient sets as approximation coefficients matrix CA and details coefficients matrices as CH, CV and CD.

b) Apply Haar wavelet transform again on CA approximation coefficient matrix to generate level 2 approximation and detail coefficient matrices. Total 4 matrices are generated in this step.

c) Apply Haar wavelet transform again on CA approximation coefficient of level 2 matrix to generate level 3 approximations and detail coefficients. Total 4 matrices are generated in this step.

d) Extract features from i^th training model and give this as an input to Mamdani type fuzzy inference system (FIS). This FIS will compute weight: FIS output, depending upon rules provided in the FIS for each input values. Working of Mamdani type FIS[13] and calculation of weight factor is explained in detail in paper[14].

e) Append i^th training data set to trndata file.

End for

Step 3: Extract features of 3D models for testing.

For j = 1 to M

a) Repeat sub steps a)-d) of step 2 for j^th testing model.

b) Create separate testdata file for j^th model.

End for

Step 4: Apply training and testing data set as an input to ANFIS model and set following parameters:

● Number and type of MFs for input as well as output.

● Number of training epochs.

● Error tolerance.

● Network type (hybrid / back propagation).

Step 5: To generate the rules.

Step 6: To train the model.

Step 7: To test the model against training data and Testing data.

Step 8: If the error difference between testing of training data and testing of testing data is very less then store ANFIS output set.

Repeat following steps for different testing models.

Step 9: Application of wavelet transform on testing model.

Apply Haar wavelet transform on the testing 3d model and generate four coefficient sets as approximation coefficients matrix CA and details coefficients matrices as CH, CV and CD.

Apply Haar wavelet transform again on CH and CV of detail coefficient matrices to generate level 2 approximation and detail coefficient matrices. Total 8 matrices are generated in this step.

Apply Haar wavelet transform again on CH and CV coefficients of level 2 matrices to generate level 3 approximations and detail coefficients. Total 16 matrices are generated in this step.

Step 10: Embedding watermark sequence

● Watermark is embedded in the middle frequency coefficient of the haar transform at 3^rd level.

● If ANFIS output value is in between 0.6 and 0.9 then the watermark is inserted into the corresponding wavelet coefficient by adding the multiplication of ANFIS output and watermark data with the wavelet coefficient vector.

Watermarked coefficient = Middle frequency coefficient + Anfis output * watermark

Step 11: Reconstruction of 3D model

Generate watermarked model by applying inverse DWT on the modified coefficients set up to level 3.

4. Watermark Extraction Algorithm

System has used a non-blind watermarking scheme in which, original model and watermarked model are needed to extract the watermark from the attacked model.

Step 1: Perform step 9 of insertion process on 3D watermarked model.

Step 2: Referring ANFIS output, the difference between original 3D model coefficient and watermarked 3D model coefficient can be calculated to extract the 3D model watermark.

3d Watermark coefficient = watermarked 3d model coefficient - original 3d model coefficient.

Analysis of extracted watermark is done by calculating the correlation and peak signal to noise ratio (PSNR).

Correlation coefficient is used to evaluate the class of the extracted watermark by computing the similarity of the original watermark (W) and the extracted watermark (W’).

PSNR is the most important technique to verify the quality of watermarked model.

5. Attacks

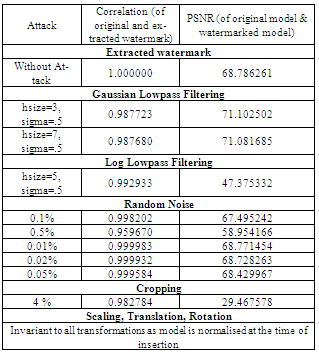
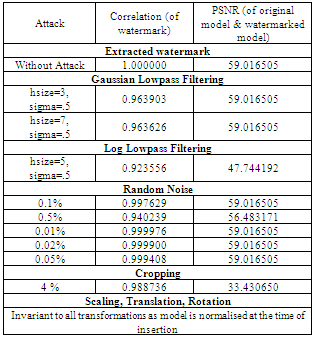
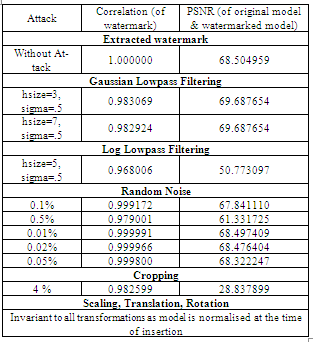
Robustness of the system is verified by applying following attacks on the watermarked model.

Similarity Transformations: This is a very common attack applied on the 3D watermarked model. This includes rotation, translation and scaling operations. As the rotation and translation transformations only change the location of the model not the actual contents, the watermarked model is safe so system is invariant to rotation and translation transformations. After applying scaling transformation on the watermarked model, magnitude of wavelet coefficients is changed, but due to normalization of model during insertion and extraction process the watermark is unaffected.

Noise analysis: Random Noise (of 0.1 %, 0.5 %, 0.01 %, 0.02 % and 0.05 %) is added to the watermarked model but still the correlation is above 0.95. Table shows the result of noise attack on watermarked models.

Smoothing attack: Gaussian and Log smoothing filters from MATLAB are applied on the watermarked models with following parameters.

● Gaussian Smoothing

hsize=3, sigma=0.5

hsize=7, sigma=0.5

● Log Smoothing

hsize=5, sigma=0.5

These filters may reduce the quality of the Watermarked model, but the extracted watermark can still represent the correct watermark.

Table 1. 3D Models

Cropping: Cropping of 4% is applied on the watermarked model but it has not destroyed the watermark fully because the watermark is spread uniformly in the original model at insertion process.

6. Results

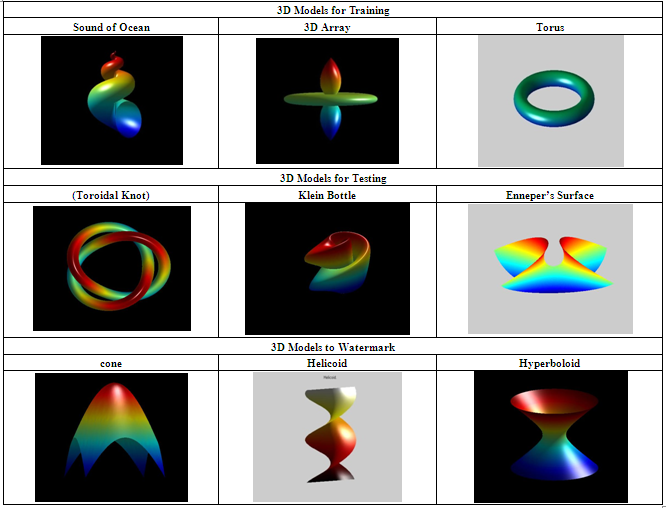
Following Tables 1, 2, 3 and 4 shows the training, testing and watermark 3d models along with the results of testing models for correlation and PSNR values.

Table 2. Test Model: Toroidal Knot, Watermark Model: Cone

Table 3. Test Model: Klein Bottle, Watermark Model: Helicoid

5. Conclusions

Use of ANFIS neural network to insert 3D model is proved to be robust. We can provide large number of 3D models for training having different features to the ANFIS model to make it more effective. Capacity of insertion of watermark is increased by increasing the size of training and testing models. Results show that the nonblind system is robust against similar transformations, noise, smoothing, and cropping attacks.

Future watermark embedding algorithms can be developed which should be invariant to all types of attacks.

Table 4. Test Model: Enneper’s Surface, Watermark Model: Hyperboloid

ACKNOWLEDGEMENTS

We would like to thank to the authors David Arnold and Bruce Wagnerfor of the Matlab Programming Textbook[15], for permitting us to use their 3D surface models for our implementation.