Naiyi Hu , Christopher J. Martinez
Department of Electrical and Computer Engineering,University of New Haven
Correspondence to: Christopher J. Martinez , Department of Electrical and Computer Engineering,University of New Haven.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The workloads in a modern CPU are becoming more diversified but a common aspect is beginning to form around the need for cryptographic algorithms.There are a number of different cryptographic algorithms for hashing, block ciphers and stream ciphers.Block ciphers have recently been linked to the DES and AES standards and are the most widely used algorithms.Stream ciphers have not been dominated by a single standard.The EU ECRYPT network has developed a set of stream cipher as part of their eSTREAM portfolio. This paper examines the eSTREAM portfolio and analysis the microarchitecture performance on the Intel Core2 Duo.Using hardware performance counters analysis is done in the areas of CPI, cache, branch prediction, and instruction-level parallelism (ILP).Our results show that the Salsa20 algorithm has the best CPI, sosemanuk is able to achieve more ILP, and branch prediction is highly accurate for HC-120, Rabbit and Salsa20. The results show the correlation between CPI with L1 cache, L2 cache, branch prediction, and ILP.
Keywords:
Performance Evaluation, Hardware Counters, Workload Characterization, eSTREAM
1. Introduction
Cryptography encryption algorithms can be divided into block ciphers and stream ciphers.The block ciphers have always been more mature in cryptanalysis and development.One of the main driving forces into the development of block ciphers have been competitions to form standards.The most popular competition was done by the NIST to create the advanced encryption standard (AES)[1].The success of AES encouraged the EU ECRYPT network to create a competition for streaming ciphers entitled eSTREAM[2,3].The program began in November 2004 and ended in April 2008.The finalist of the eSTREAM was divided into two categories Profile 1 for software applications and Profile 2 for hardware applications[2, 3].The eSTREAM project did not select only one finalist to be the best cipher algorithm but presented four software focus algorithms that meet the high requirements for crypto-integrity and high speed processing. The performance benchmark was that the eSTREAM algorithms have performance that significantly outruns the AES in a stream cipher mode. Each eSTREAM cipher is aimed to have high encryption stream that can encrypt large amounts of data with only a single initialization. Since 2008 the cipher algorithms have not undergone any additional research on the software performance of the eSTREAM finalist.All the algorithms did have performance studies done during the competition period. All the candidates were tested on a Pentium 4 computer or older CPU generation. CPU microarchitecture has rapidly developed since the Pentium 4 and have seen a number of new generations of CPUs.B. Bernstein[4] presented a paper that asked the question which eSTREAM cipher provides the best software speed.The paper explored the processing speed of the algorithms on a wide set of CPUs. The paper used Intel Core2, IBM Cell, Athlon 64 X2, Pentium M, Pentium 4, PowerPC G5, PowerPC G4 and UltraSPARC III.[4] only gives performance in terms of cycle counts per encrypted byte. The results show which algorithm is the fastest but does not give any insight into why one CPU performs better than other CPUs. The purpose of this project is to explore the microarchitecture utilization on a modern CPU.Using the Core2 Duo, we are able to give all the details on how each component of the CPU (branch predictor, cache, etc) is used in the operation of the cipher.This paper presents a detailed performance analysis ofthe four stream ciphers from the eSTREAM PortfolioProfile 1. The test was conductedon aIntel Core2 Duo CPU computer. By analyzing the raw performance data, which were collected with theIntel VTune Amplifier XE 2011, important information on cache, branch prediction and exploited instruction-level parallelism (ILP)were obtained.The information presented in this paper can be used to optimize software stream ciphers implementation and to give guidance to researchers working on future stream ciphers to know how to best use the features found in the Intel CPU.Similar studies have done on other cryptography algorithms that examined the hardware counters on AES, DES, Blowfish, etc. in[12-15]. The work on eSTREAM is important since the other papers have not investigated streaming algorithms.The rest of the paper is organized as follows. In section 2, we give a brief explanationon the background of each cipher. Theconfiguration of the testing environment isdescribed in section 3. Section 4 analyzes the data collected from all workloads. And section 5 gives the conclusion.
2. Background on eSTREAM Cipher
The stream ciphers used in this paper were chosen from the eSTREAMPortfolio Profile 1. They are HC-128, Rabbit, Salsa20 and SOSEMANUK. All the four ciphers aresynchronous stream ciphers, and each cipher is implemented with two functions: an internal functionto generatethe keystream and an output function that encrypts the plaintext by combining it with the keystream using exclusive-or operation (XOR), as shown in Fig. 1.The decryption for the four ciphers is the same as encryption.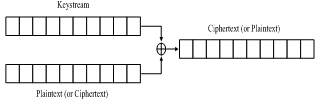 | Figure 1. Stream cipher encryption (or decryption) |
2.1. HC-128
HC-128 is a stream cipher designed for 128-bit security that is a variant of HC-256, proposed by HongjunWu[5]. HC-128 is considered the best algorithm that meets the intended goals of the eSTREAMprogram[2]. HC-128 uses two S-boxesin its keystream generation algorithm. Each S-box has 512 32-bit elements andis updated every 1024 steps. At each step, one element of the S-boxes is updated and one 32-bit output is generated. Since HC-128 is table-driven which leads to more time in order to initialize the cipher.Fig. 2 shows an overview of HC-128. S-box P is in use when i(mod 1024) is less than 512; S-box Q is in use when i(mod 1024) is greater than 512.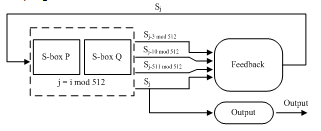 | Figure 2. HC-128 stream cipher |
2.2. Rabbit
The stream cipher Rabbit was designed by Martin Boesgaard, MetteVesterager, Thomas Christensen and Erik Zenner[6]. It uses a key of 128-bit length like HC-128. Rabbit does not have an S-box. Instead, it has an internal state that consists of eight 32-bit state variables, eight 32-bit counters and one counter carry bit.The eight counters are updated every time before iterating to the internal system, defined as the diagram in Fig. 3.Cj,i denotes the counter variable j at iteration i, and Coi denotes the carry bit. The aj are eight constants.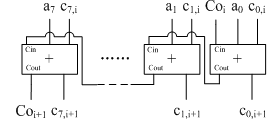 | Figure 3. The counter of the Rabbit stream cipher |
The eight state variables are updated in the iteration by eight couplednon-linear functions. All state variables only depend on their corresponding counters and the previous state variables, so they can be updated simultaneously.With each iteration, Rabbit generates a block of keystream of 128-bit using the internal state variables. Fig. 4 shows an overview of Rabbit.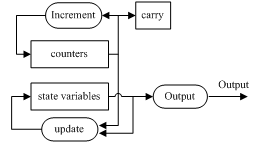 | Figure 4. Rabbit stream cipher |
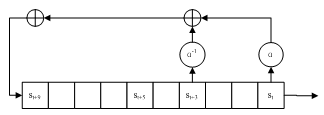 | Figure 5. The LFSR of SOSEMANUK cipher |
2.3. SOSEMANUK
The stream cipher SOSEMANUK was designed by C. Berbain and et. al.[7].SOSEMANUK uses an LFSR of ten 32-bit elements and a finite state machine (FSM) to hold its internal state.The design of the LFSR is influenced by the stream cipher SNOW 2.0[8]. See Fig. 5 for the diagram of theLFSR. For any time t ≥ 1, st to st+9 denotes the ten elements in the LFSR. At every step, a new value, denoted as st+10, is computed with the following equation:st+10 =st+9⊕ɑ-1st+3⊕ɑstand the LFSR is shifted. The multiplication and division operation in the LFSR corresponds to a shift operation followed by an XOR operation with a 32-bit mask.The finite state machine consists of two 32-bit registers. At each step, it takes three elements (st+1, st+8, st+9) from the LFST to produce a 32-bit output, denoted as ft, and update the two registers.For every four output values from the FSM, denoted as ft, ft+1,ft+2 andft+3, an S-box application is applied to produce a four 32-bit output, denoted as zt, zt+1,zt+2, zt+2. The output transformationis derived from Serpent1[9]. SOSEMANUK generates a 128-bit block of keystream by combining the output zt, zt+1,zt+2,zt+2 with the first four elements in the LFSR using XOR operation. Fig. 6 shows an overview of the SOSEMANUK stream cipher.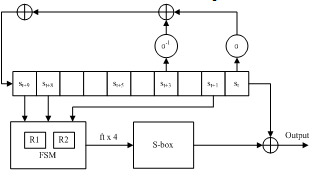 | Figure 6. SOSEMANUK stream cipher |
2.4. Salsa20
Salsa20 was designed by Daniel J. Bernstein[c10]. The core of Salsa20 cipher is a hash function. Unlike the three ciphers introduced about above, Salsa20 does not use the portion of the previous states to update its internal state. Instead, a 64-bit counter is used to create sequential blocks of keystream. Salsa20 takes a 128-bit (or 256-bit) secret key, a 64-bit nonce and the 64-bitcounter to generate a 64-byte block of keystream at each step and increase the counter by 1 after that.Fig. 7 shows the overview of Salsa20. Because each state does not depend on the previous ones, this greatly increases the parallelism in Salsa20.Modern computer architecture can exploit such parallelism to improve the performance. In order to eliminate the correlation between the output and the key, the hash function uses a lot of rotation operations.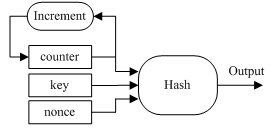 | Figure 7. Salsa20 stream cipher |
3. Testing Environment
The test is performed on anIntel Core2 Duo CPU computer system. The detailed characteristics of the testing environment are described inTable 1. The Intel Core2 Duo is a 32-bit superscalar CPU that contains 2 logical CPU cores, an L1 cache that is split for instructions and memory, and L2 cache. The CPU can handle instructions 5 wide for decoding, 4 wide for renaming, 5 wide for retiring, 6 instructions per cycle, and 32 micro-ops scheduler[11].| Table 1. Testing platform configuration |
| | Processor | Intel Core2 Duo CPU E7500 | | Clock Frequency | 2.93GHz | | Number of cores | 2 | | Instructions sets | MMX, SSE, SSE2, SSE3, SSSE3, SSE4.1, EM64T, VT-x | | L1 Data cache | 2 x 32 KBytes, 8-way set associative, 64-byte line size | | L1 Instruction cache | 2 x 32 KBytes, 8-way set associative, 64-byte line size | | L2 cache | 3072 KBytes, 12-way set associative, 64-byte line size | | Memory Type | DDR2 | | Memory Size | 2048 MBytes | | Memory Frequency | 399.0 MHz (2:3) | | Operating System | Microsoft Windows XP ProfessionalVersion 2002SP3 |
|
|
The four stream ciphers were compiled withMicrosoft C/C++ compiler version 15 using optimization level O2 (maximum speed).Each cipher took a 128-bit secret key and was fed with a message of 600 Mbytes. The bench mark only contained the encryption process of the ciphers. The key and IV setup benchmark were not run.| Table 2. Testing platform configuration |
| | Name of the Counter | Definition | | BR_INST_RETIRED.ANY | Retired branch instructions. | | BR_INST_RETIRED.MISPRED | Retired mispredicted branch instructions (precise event) | | CPU_CLK_UNHALTED.CORE | Core cycles when core is not halted. | | INST_RETIRED.ANY | Instructions retired. | | L1D_REPL | Cache lines allocated in the L1 data cache. | | L1I_MISSES | Instruction Fetch Unit misses. | | L2_LINES_IN.BOTH_CORES.ANY | L2 cache misses. | | RESOURCE_STALLS.BR_MISS_CLEAR | Cycles stalled due to branch misprediction. | | RS_UOPS_DISPATCHED | Micro-ops dispatched for execution. | | UOPS_RETIRED.ANY | Micro-ops retired. | | UOPS_RETIRED.FUSED | Fused micro-ops retired. |
|
|
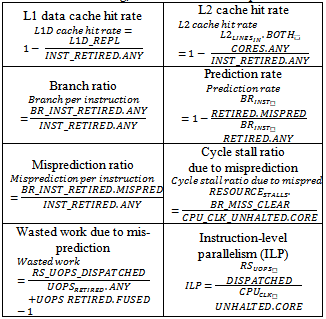
We used IntelVTune Amplifier XE2011 to collect performance data in the test.The VTuneAmplifier XE collects performance data using event-driven sampling technique.It can work with very low overhead and impacts little on the programs being tested.Each program was run several times and we used the average value to improve the accuracy of the collected data.Table 2 lists all the Intel Core2 Duo CPUperformance counters that are used in this paper.Using the performance measurements in Table 2 the following equations were used to calculate performance measurements for branching, cache and instruction parallelism.
4. Performance Results and Analysis
Each of the eSTREAM algorithms were examined to see the performance of the microarchitecture on the instructions executed, CPI, cache, ILP, and branching.The performance measurements give details on how the cipher algorithm is executing and can lead to optimization in performance.
4.1. Overview of the Performance Result
The overall performance of the cipher algorithm can be viewed by the clock cycles per instruction (CPI).The CPI is not the best or only measurement that can be used but it is the one single measurement that can give a complete overview of CPU performance.To find the CPI measurement the number of retired instructions are needed for each cipher algorithm. The retired instructions refer to those instructions that are executed completely and update the machine state. This does not include instructions that are partially executed and discarded due to branch misprediction (see section 4.3). Fig. 8 shows the number of retired instructions of the four stream ciphers.This value reflects the complexity of the stream cipher in some extend. It was observed thatSalsa20 ran the most number of instructions of the four ciphers.This wasbecause that Salsa20 used a huge hash function which involved lots of rotation operations.HC-128 ran with the least number of instructions, because it used two large S-boxes instead of complicated operations to achieve the security requirement. Every instruction that is executed is composed of a number of micro-operations (micro-ops).The micro-ops allow for additional out-of-order execution. The total number of micro-ops that can be executed is shown in Fig. 9.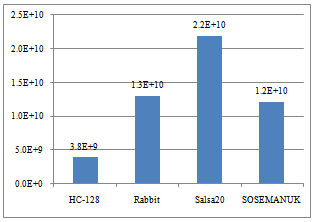 | Figure 8. Number of retired instructions of the workloads |
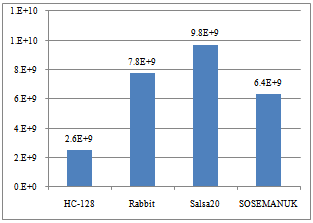 | Figure 9. Number of retired micro-ops of the workloads |
The average CPI is one of the most important metrics that reflect overall software performance. Fig. 10 shows the CPI values of the workloads.It was observed that all the four ciphers havea CPI from 0.4 to 0.7, with Salsa20 yielding the lowest CPI value of 0.445 and HC-128 yielding the highest CPI value of 0.673. This disparity could be attributed to their cache performance, branch misprediction rate and exploited program parallelism. These factors will be discussed in detail in the following of section 4.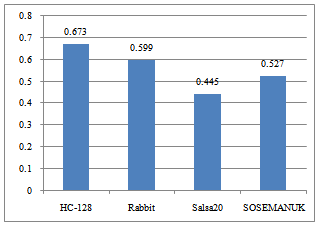 | Figure 10. CPI values of the workloads |
The CPI values are the indication of how effective the CPU hardware is running and does not factor in the execution time. The execution time of the algorithms was as follows: HC-128 required 5.04s, Rabbit required 8.568s, Salsa20 required 9.872s and Sosemanuk required 7.518s. The execution time is a result of the cipher algorithm not the microarchitecture of the CPU [2]. The results in the following section can provide insight on to how the execution time could be reduced by better utilizing the microarchitecture.
4.2. Cache Performance
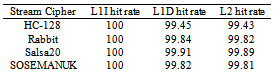
A contributor to poor CPI performance is related to the cache performance. A miss in cache can result in long latency operations in the pipeline. Especially when there are other operations depending on the results of such operations, significant stalls could occur. Table 3 shows the cache hit-rate of the four ciphers. It was observed that there werevery few misses in L1 instruction (L1I) cache for all workloads. This was because the code sizes of the four cipherswere allrelatively small (less than 32k bytes) and could fit into the L1I cache. When calculating the hit-rate the compulsory misses were few resulting in not being able to accurately calculate any miss-rate with precession with the sampling done by VTune.The hit-rate was shown as 100% for this reason. It was also observed that both cache hit rates were very good for all the four ciphers. The cache hit rate for HC-128 wasrelatively low, but could still be considered good. This indicated that the four stream cipher all had a small working set and they all benefitedgreatly from caches. Hence, the cache hit rate was not the main reason that caused the disparity in CPI values.The hit rate for the L1 data cache and L2 cache were very similar across all four ciphers. The main reason was that each cipher used the same data set. Since the stream operation required each set of data to be access in the same order the only reason for additional data misses are in the internal variables of the algorithm. To further reduce the data miss rate the programmer must examine how to better align internal variables to fit in the same blocks of cache. Table 3. L1 and L2 cache hit rate
 |
| |
|
4.3. Branch Misprediction
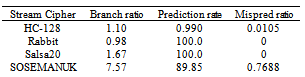
Branch prediction could significantly lower the run time performance of software. Table 4 shows the prediction rate for the four ciphers.VTune Amplifier failed to detect any branch mispredictions for Rabbit and Salsa20, so it was considered a hundred percent correct prediction for them. It was observed that the SOSEMANUK stream cipher had the highest branch ratio and the highest misprediction ratio.Table 4. Branch misprediction rate of the workloads
 |
| |
|
The penalty of misprediction can be decomposed into two parts: cycle stalls and wasted work.The stall happens from the time when misprediction is detected till the branch and all older micro-ops are retired.Fig. 11shows the cycle stalls ratio due to misprediction.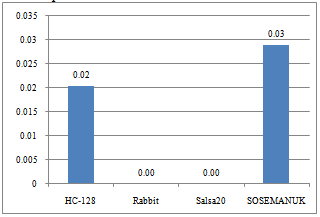 | Figure 11. Cycle stalls ratio due to branch misprediction |
The wasted work refers to those cycles wasted in executing a wrong branch path.Fig. 12 shows an estimate for the waste work.The wasted work ratio for SOSEMANUK was as high as 18% due to its high misprediction, while the other three ciphers were considered havingno wasted work.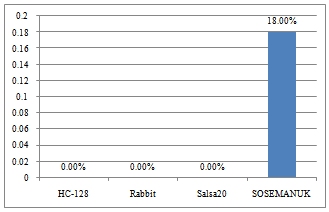 | Figure 12. Wasted work due to branch misprediction |
The data indicates that even low misprediction rate can cause great penalty. SOSEMANUK had a cycle stall ratio of 3% and did approximate 18% wasted work due to 0.8% branch misprediction. HC-128 had a cycle stall ratio of 2% due to 0.01% branch misprediction.
4.4. Instruction-level parallelism (ILP)
The software performance can be greatly improved on a superscalar CPU by exploiting the parallelism within it. In this study, the ILP is defined as the average number of micro-op being dispatched for execution per cycle.The processor used in this study has 6 dispatch ports [10], so theoretically it can reach an ILP of 6. However, in practical, the amount of exploited parallelism depends greatly on the structure of the software. Data dependency could significantly limit the ILP. For the ILP we defined above, control dependency does not lower the ILP, but the work done in thewrong path will be counted as wasted work if the branch is mispredicted. Fig. 13 shows the ILP calculated for the four stream ciphers in this study.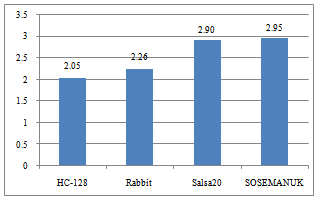 | Figure 13. The exploited ILP in the workloads |
It was observed that the exploited ILP in Salsa20 and SOSEMANUK was higher. This indicates that less data dependencies were involved in those two ciphers. In fact, the high parallelism in Salsa20 is obvious. The Salsa20 cipher uses integer counter mode (see section 2.4) to generate keystream instead of using output feedback mode (OFB). So each internal stage does not depend on previous stages and can be computed independently. The other three ciphers all use OFB mode.
4.5. Analysis of the Correlation with CPI
By looking at each factor separately, we cannot conclude their correlation with the CPI. In this section, we put them together to find out the correlation coefficient (see Table 5).The table shows that there is a high correlation between CPI and ILP.This is due to the fact that more parallelism should allow more instructions to be completed each cycle.In the eSTREAM ciphers the branch prediction rate has no strong correlation with the CPI.Only one algorithm SOSEMANUK had a large amount of wasted work due to branching in the wrong direction.Both the L1 and L2 cache has the same impact on CPI. Table 5. Correlation between CPI and other metrics
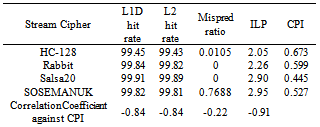 |
| |
|
It was observed that SOSEMANUK and Salsa20 were similar in cache hit rate and ILP. However, they had a difference of as large as 0.082 in CPI and it was most likely attributed to the disparity (0.8%) in branch misprediction rate. This again proved the conclusion we had in section 4.3: even little branch misprediction can cause great penalty. So we can conclude thatthe misprediction rate in SOSEMANUK lead to the increase in CPI.The amount of exploited ILP also showed high negative correlation with CPI. It was observed that the exploited ILP in Salsa20 and SOSEMANUK reached as high as 2.90. This could be the major reason why they yielded a lower CPI of the four ciphers. Similarly, HC-128 and Rabbit yielded a higher CPI due to their low exploited parallelism.The cache hit rate for the four ciphers are close enough to not make noticeable disparity in their CPI.
5. Conclusions
In this paper, we analyzed a set of stream ciphers from the eSTREAM project on an Intel Core2 Duo CPU computer. All stream ciphers have a small working set so they all have a similar high cache hit rate. Effectively exploiting the capability of parallel execution in modern computer systemsis one of the key factors for low CPI. However, even a very small number of branch mispredictions can create a large amount of wasted work, and hence significantly undermine the overall performance of stream ciphers. This suggests stream cipher designers need to reduce the number of branches in cipher algorithm and utilize the new features of parallel execution of the computer architecture to achieve better performance.
References
| [1] | AES, the Advance Encryption Standard, NIST, FIPS-197. |
| [2] | S. Babbage, et.al., “The eSTREAM Portfolio,” eSTREAM ECRYPT Stream Cipher Project, Final Report 2008/, 2008, http://www.ecrypt.eu.org/stream. |
| [3] | A. Billet, New Stream Cipher Designs: The eSTREAM Finalists, Lecture Notes in Computer Science, Vol 4986, Springer, 2008. |
| [4] | Daniel J. Bernstein, “Which phase-3 eSTERAM ciphers provide the best software speeds?”,eSTREAM ECRYPT Stream Cipher Project, Report 2008/013, 2008,http://www.ecrypt.eu.org/stream. |
| [5] | H.Wu, A New Stream Cipher HC-256. In B. Roy and W. Meier, editors, Proceedings of FSE 2004, Lecture Notes in Computer Science, Volume 3017, pages 226-244, Spring 2004. |
| [6] | M. Boesgaard, M. Vesterager, T. Pedersen and O. Scavenius. Rabbit: A new High-Performance Stream Cipher. In T. Uohansson, editor, Proceedings of FSE 2003. |
| [7] | C. Berbainet. al., “SOSEMANUK, a fast software-oriented stream cipher,” eSTREAM, the ECRYPT Stream Cipher Project, Report 2005/027, 2005. |
| [8] | P.Ekdahl and T. Johansson.,“A new version of the stream cipher SNOW”, in Selected Areas in Cryptography – SAC 2002, volume 2295 of Lecture Notes in Computer Science, pages 47-61. Springer-Verlag, 2002 |
| [9] | E.Biham, R. Anderson, and L. Knudsen. SERPENT, “A new block cipher proposal”, in Fast Software Encryption – FSE’98, volume 1372 of Lecture Notes in Computer Science, pages 222-238. Springer-Verlag, 1998. |
| [10] | Daniel J. Bernstein, “The Salso20 family of stream ciphers,” New stream cipher designs: the eStream finalists, edited by M. Robshaw and O. Billet, Lecture Notes in Computer Science, vol. 4986, pg. 84-97, Springer, 2008. |
| [11] | Jack Doweck, “Inside Intel Core Microarchitecture,” Proceedings of Hot Chips 18 A Symposium on High Performance Chips, 2006. |
| [12] | Jason Poovey, Thomas Conte, Markus Levy, and Shay Gai-On, “A Benchmark Characterization of the EEMBC Benchmark Suite,” IEEE Micro, p. 18 – 29, Sept 2009. |
| [13] | K. Hoste and L. Eeeckhout, “Comparing Benchmarks using Key Microarchitecture-Independent Characteristics,” IEEE Workload Characterization Symposium, 2006. |
| [14] | Aniruddha Desai and Jugdutt Singh, “Architecture Independent Characterization of Embedded Java Workloads,” IEEE Computer Architecture Letters, 2009. |
| [15] | A. Fiskiran and R. Lee, “Performance Impact of Addressing Modes on Encryption Algorithms,” International Conference on Computer Design, 2001. |














 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML