-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Advances in Computing
p-ISSN: 2163-2944 e-ISSN: 2163-2979
2012; 2(1): 6-11
doi:10.5923/j.ac.20120201.02
Multi Scale Spin Glass Based Portfolio Selection
Majid Vafaei Jahan
Department of Software Engineering, Mashhad Branch - Islamic Azad University, Mashhad, Iran
Correspondence to: Majid Vafaei Jahan, Department of Software Engineering, Mashhad Branch - Islamic Azad University, Mashhad, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
One of the techniques to resolve the problem more quickly is using the multi-scale spatial dimension reduction. In classical theory, system analysis based on multi-scaling is extremely difficult, because it is dependent on the behavior of every component analysis and understanding the relationship between them. The new achievements in this field show that most systems cannot be scaled at any condition. Regardless to this property of the system, Kadanoff's theory shows a necessary condition of scaling. Based on this theory, the best condition of scaling occurs in the phase transition condition at the critical temperatures of material. In this condition, upper-scale system behavior is approximately similar to the main-scale system behavior. This article is benefited from this theory and is presented the new algorithm that is named Simulated Annealing Multi-Scaling (SAMS). This algorithm is based on the spin glass paradigm to solve the NP-complete portfolio selection problem as a case study. Due to many relationships between stocks, the problem scaling, is equivalent to loss of part of the data, hence the possibility to achieve the ground state decline so much. By using this theory, it is shown that the best time to change the scale of the problem with minimum error occurs during its phase transition. Tests on five major stock exchange data show, this algorithm, in addition to confirming Kadanoff's theory in application, has more convergence speed than traditional methods such as SA and also, provides the possibility of using parallel processing in optimization problems.
Keywords: Ising Spin Glass Model, Portfolio Selection Problem, Multi-Scaling, Kadanoff's Scaling Picture Theory, Parallel Processing
Cite this paper: Majid Vafaei Jahan, Multi Scale Spin Glass Based Portfolio Selection, Advances in Computing, Vol. 2 No. 1, 2012, pp. 6-11. doi: 10.5923/j.ac.20120201.02.
Article Outline
1. Introduction
- Most systems around us have superiority complex nature[1]. For adequate understanding of these systems, only recognition of its principal components is not enough. Because of identifying the relationship between them is more difficult than recognizing its individual components[1] and specially, it is more complicated for systems with emergent behavior[2,3]. In this case, heuristic algorithms such as genetic algorithm or simulation techniques such as Monte- Carlo methods usually help to find the optimal system's state. Because of the inherent low speed specification (with regards to accuracy) of these algorithms, scientists are encouraged to representing new methods to reach both accuracy and speed[4,5]. One of these techniques considered in this direction uses a physical property of materials such as multi-scaling property[6]. Since, scaling cannot be done at any condition and depend on recognizing individual system's components[7,8]; Kadafnoff's theory can help us to find the best time and conditions of scaling. Based on Kadanoff's theory, the best scaling condition of system is in phase transition at the critical temperatures[8]. In other words, the best time to build up the upper-scale of a system (to reduce the dimensionality of system's space) is during its phase transition. Despite, the number of variables in upper scale is less and relationships between them are weaker, and require less processing time[9] to find optimal state of the problem in upper scale; both systems (main scale and upper scale) have the same functional behavior, and the energy equations are used without significantly changes. Hence it is enough to provide the phase transition condition for the problem and rescale the problem into upper-scale to find the optimal state faster.In this paper, a new optimization algorithm that is named SAMS based on spin glass scaling and Kadanoff's theory is presented and as a case study, the portfolio selection problem is solved. So first, the portfolio selection problem is mapped into long range spin glass as mentioned in paper[10], and then the glass is placed in phase transition situation. In this condition, the scale of the glass is changed into a upper scale glass and some smaller main scale glass. For each generated glasses, ground state is found with one of the heuristic methods such as simulated annealing (SA) and finally renormalized again to show the found ground state of the problem.The experiments show, the speed of finding ground state has increased about fifty percent regardless having computation overhead.So first, in Section 2, concepts of renormalization and multi-scaling are described, in Section 3, the proposed SAMS algorithm based on the kadanoff's theory and multi- scaling is explained. In Section 4, the portfolio selection problem and Markowitz model are defined and in Section 5, the portfolio selection solution by using long range spin glass, which is described in paper[10], is expressed again. Finally, in Section 6, experimental results and conclusions are presented.
2. Renormalization Group and Multi-Scaling
- Renormalization group transformation is a process that all algorithms and formulas of a system in scale
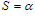 become represented into the algorithms and formulas in scale
become represented into the algorithms and formulas in scale 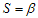 [8].
[8]. 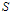 shows the scale factor and its numerical value is smaller than or equal to 1 and is greater than zero. Value 1, represents the main glass and, smaller than 1, indicates the glass in upper-scale. In renormalization group theory, first, the glass is clustered. It is assumed that each cluster of spins is a new spin in upper-scale glass. In new glass, with less spins, it is assumed the energy equations remain constant during the scaling and it can be used for upper-scale without any changes. It should be mentioned that there are various clustering algorithms and can be studied as sample in[9,11]. This article, dose not talks about the glass clustering; the desired clustering is more like making mesh. In other words, kind of division and regional position on the glass is performed. After clustering, for each smaller glass and upper- scale glass, ground state is calculated using heuristic algorithm. This operation can be performed in several stages as much as scaling allows.
shows the scale factor and its numerical value is smaller than or equal to 1 and is greater than zero. Value 1, represents the main glass and, smaller than 1, indicates the glass in upper-scale. In renormalization group theory, first, the glass is clustered. It is assumed that each cluster of spins is a new spin in upper-scale glass. In new glass, with less spins, it is assumed the energy equations remain constant during the scaling and it can be used for upper-scale without any changes. It should be mentioned that there are various clustering algorithms and can be studied as sample in[9,11]. This article, dose not talks about the glass clustering; the desired clustering is more like making mesh. In other words, kind of division and regional position on the glass is performed. After clustering, for each smaller glass and upper- scale glass, ground state is calculated using heuristic algorithm. This operation can be performed in several stages as much as scaling allows.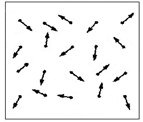 | Figure 1. Glass with scale factor, in this glass, there are twenty spin |
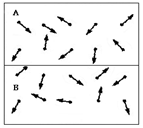 | Figure 2. Glass with scale factor, a glass with twenty spin renormalized to a glass with 2 spin that each one has ten spin |
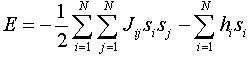 | (1) |
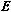 is the energy of the glass and
is the energy of the glass and 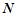 is total number of spins in the glass. The sum
is total number of spins in the glass. The sum 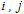 runs over all pairs of nearest neighbors (in this paper, glass is long range spin glass, and each spin is nearest neighbor of all other spins),
runs over all pairs of nearest neighbors (in this paper, glass is long range spin glass, and each spin is nearest neighbor of all other spins), 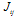 denotes the strength of the bond connecting spins
denotes the strength of the bond connecting spins 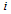 and
and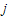 .
. 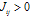 describes a ferromagnetic interaction, while
describes a ferromagnetic interaction, while 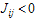 describes an anti-ferromagnetic interaction. The quantity
describes an anti-ferromagnetic interaction. The quantity 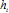 is the external field acting on spin
is the external field acting on spin 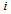 and describes the energy due to the spin's orientation. Also, the factor
and describes the energy due to the spin's orientation. Also, the factor 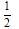 corrects for double counting of the interaction between every two neighboring spins. Here the task is to find a spin configuration
corrects for double counting of the interaction between every two neighboring spins. Here the task is to find a spin configuration 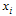 that minimizes the energy of the spin glass, given
that minimizes the energy of the spin glass, given 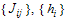 For calculating the energy of upper-scale glass, the strength of the bond between spins
For calculating the energy of upper-scale glass, the strength of the bond between spins 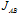 and external field
and external field 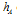 energy must first be calculated. For this purpose, formula (2) is used for calculating the energy between spins and formula (3) is used for calculating the external field energy per spin[9].
energy must first be calculated. For this purpose, formula (2) is used for calculating the energy between spins and formula (3) is used for calculating the external field energy per spin[9].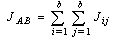 | (2) |
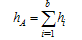 | (3) |
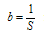 is the total spin of each cluster and
is the total spin of each cluster and 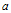 is the total spin in glass in upper-scale. So, the total number of spins of main scale glass is equal to
is the total spin in glass in upper-scale. So, the total number of spins of main scale glass is equal to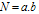 .Considering the above definitions and regarding to the renormalization theory the energy per glass in upper-scale is calculated as follows:
.Considering the above definitions and regarding to the renormalization theory the energy per glass in upper-scale is calculated as follows: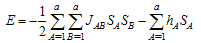 | (4) |
3. SAMS Algorithm
- In Fig. (1), a summery of SAMS algorithm is shown. This algorithm is a combination of SA and multi-scale techniques regards to the renormalization process and used for solving optimization problems. SA is used for finding optimal state of each glass and scaling is used for creating glasses with different scale.As shown in Fig. (3), first, glass is placed in phase transition condition and renormalized. In this condition, an upper-scale glass along with several smaller glasses is produced. For all produced glass, SA algorithm is applied. The results are glasses that are locally optimal. Now, the result of upper-scale glass is applied on main-scale glass, (by multiplying the amount of each spin in upper-scale glass), to demonstrate the glass's ground state.Experiments show, the optimal glass's state, in regards to SAMS algorithm, is closer to ground state; but it is not ground state yet. The reason is clear: the renormalization formulas are approximate and accuracy is reduced from main-scale to upper-scale. Even, these conditions are worse for more scaling levels that cause glass can not specify the ground state clearly.
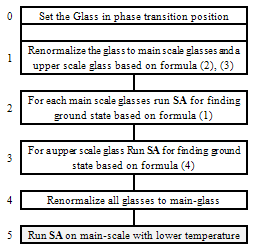 | Figure 3. Algorithm SAMS, based on Kadanoff's theory. Row 5, can be executed after renormalization for finding glass ground state; it is not part of SAMS algorithm |
4. Portfolio Selection Problem
- Let us consider the Markowitz mean-variance model[13, 14] for the portfolio selection problem as stated below,
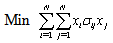 | (2) |
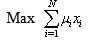 | (3) |
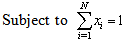 | (4) |
 | (5) |
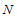 is the number of different assets,
is the number of different assets, 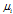 is the mean return of asset
is the mean return of asset 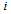 , and
, and 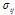 is the covariance between returns of assets
is the covariance between returns of assets 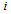 and
and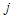 . The decision variable
. The decision variable 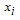 represents the fraction of capital to be invested in asset
represents the fraction of capital to be invested in asset  . Eqs. (2)-(3) are two cost functions that should be solved with constraints (4) and (5).
. Eqs. (2)-(3) are two cost functions that should be solved with constraints (4) and (5). 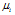 is the mean return of asset
is the mean return of asset 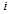 in
in 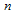 intervals of time, i.e.
intervals of time, i.e. 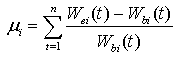 , where
, where 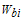 is the
is the 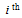 asset value at the beginning and
asset value at the beginning and 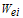 is the
is the 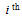 asset value at the end of each interval.In this paper we change the multiobjective problem into a multimodal problem with single objective function as follows,
asset value at the end of each interval.In this paper we change the multiobjective problem into a multimodal problem with single objective function as follows,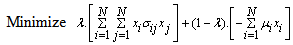 | (6) |
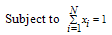 | (7) |
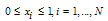 | (8) |
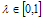 be the risk aversion parameter. If
be the risk aversion parameter. If 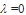 then Eq. (6) represents maximum portfolio mean return (without considering the variance) and the optimal solution will be formed only by the asset with the greatest mean return. The case with
then Eq. (6) represents maximum portfolio mean return (without considering the variance) and the optimal solution will be formed only by the asset with the greatest mean return. The case with 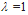 represents minimizing the total variance associated with the portfolio (regardless of the mean returns) and the optimal solution will typically consist of several assets. Any value of
represents minimizing the total variance associated with the portfolio (regardless of the mean returns) and the optimal solution will typically consist of several assets. Any value of 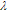 inside the interval (0,1) represents a tradeoff between mean return and variance, generating a solution between the two extremes,
inside the interval (0,1) represents a tradeoff between mean return and variance, generating a solution between the two extremes, 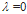 and 1.
and 1.5. Solving Portfolio Selection Problem Using Spin Glass Paradigm
- To present our method, we initially map the portfolio selection problem into a spin glass computational model and then find its ground state by looking at the objective function, Eq. (6), of the portfolio selection problem and comparing it with the spins energy function Eq. (1) of the spin glass model. We obtain the values for the interaction strength as follows [10]:
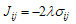 | (9) |
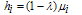 | (10) |
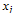 represents the proportion of capital to be invested in asset i; and in spin glass, we can define
represents the proportion of capital to be invested in asset i; and in spin glass, we can define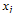 to be the state of spin i. So the problem of portfolio selection can be solved by minimizing the mapped function as in Eq. (6).For finding the minimum of optimization function Eq. (6) with regard to constraints (7)-(8), we first randomly place the possible assets into a long range glass (Full connection glass). All of the spins in this structure are initialized to random values. Therefore, we can use some heuristic algorithm or methods such as SA to select the best assets by finding the ground state or minimum energy of the glass.According to the SA algorithm, a spin is chosen randomly at every flip and the value of the selected spin is increased by
to be the state of spin i. So the problem of portfolio selection can be solved by minimizing the mapped function as in Eq. (6).For finding the minimum of optimization function Eq. (6) with regard to constraints (7)-(8), we first randomly place the possible assets into a long range glass (Full connection glass). All of the spins in this structure are initialized to random values. Therefore, we can use some heuristic algorithm or methods such as SA to select the best assets by finding the ground state or minimum energy of the glass.According to the SA algorithm, a spin is chosen randomly at every flip and the value of the selected spin is increased by  . Accordingly, the value of neighboring spins changes to meet the constraints (7) and (8).For the heating and cooling schedule, procedures related to SA are used, as in[15,16]. To do so, the temperature of the network is considered to be initially set to
. Accordingly, the value of neighboring spins changes to meet the constraints (7) and (8).For the heating and cooling schedule, procedures related to SA are used, as in[15,16]. To do so, the temperature of the network is considered to be initially set to 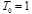 (at high temperatures all states can occur). Each time the changes are applied the temperature gradually decreases until it reaches near zero. Temperature variations can be governed by the following formula,
(at high temperatures all states can occur). Each time the changes are applied the temperature gradually decreases until it reaches near zero. Temperature variations can be governed by the following formula, 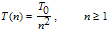 | (11) |
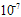 .
.6. Experimental Results
- Experiments on the benchmark data were originally performed in[17]. These benchmark data are presented in text file format as follows:Number of assets (N); and for each asset i (i=1,...,N): mean return as well as standard deviation of return; for all possible pairs of assets: i, j, correlation between asset i and asset j. The above data were taken from five major stock exchange markets, during the time period extending from March 1992 to September 1997. These five stock exchange markets include Hang Seng in Hong Kong (31 assets), Deutscher Aktien Index (DAX100) in Germany (85 assets), Financial Times London Stock Exchange (FTSE100) in Britain (89 assets), Standard & Poor's (S&P100) in USA (98 assets), and Nikkei in Japan (225 assets). Probability density function (pdf) of covariance P(J) of each stock market for the given data has been shown in Fig. (4).As can be observed, the P(J) of the five given stock markets have small mean and variance.All of the experiments were performed using Borland Delphi 6.0 running on a Pentium 2.4 GHz PC, under Windows XP operating system.
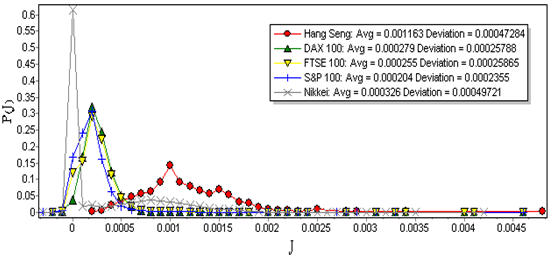 | Figure 4. Probability density functions for covariances between assets in 5 major stock markets from 1992 to 1997 from data in [17] |
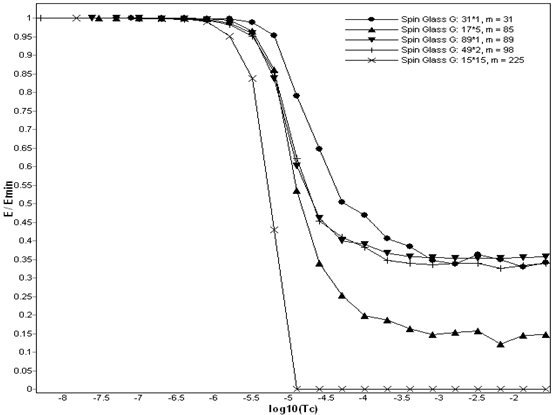 | Figure 5. Phase Transition Temperature for five stock markets [17], this temperature is the same for all stocks |
6.1. Phase Transition for Portfolio Selection Problem
- A phase transition typically refers to a transformation of a thermodynamic system from one state to another. This transformation is typically marked by a sudden change in some physical property that is the result of some small change in what is called an order parameter (e.g., temperature)[18,19]. Phase transition temperature in spin glasses is a sudden change that occurs in a state of glass. In other words, at this temperature, the probability of finding the ground state of the glass decreases significantly and glasses' states are unlikely to be a ground state. Fig. (8) illustrates phase transition temperature of spin glasses applied to the portfolio selection problems. As shown in this figure, the probability of reaching ground state (
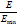 ) is equal to 1 in low temperatures, where E is the amount of glass energy and
) is equal to 1 in low temperatures, where E is the amount of glass energy and 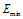 is the actual minimum of the energy function. As temperature rises, glass energy also changes and the probability of reaching ground state is expected to gradually decrease. However, this drop is delayed until phase transition, where a sudden drop occurs. After phase transition temperature (critical temperature), the probability of reaching ground state decreases significantly. As shown in Fig. (8), this temperature is approximately 5.8* 10-5 for all of the five mentioned stocks. At this temperature, system is not in ground state and selecting any state as answer of the problem is unlikely to be a ground state.After the spin glass was placed in phase transition condition, renormalization process is performed. In this case, the glass is divided into several smaller glasses. Also according to formulas (2) and (3), a upper-glass scale is produced. Now, SA algorithm applies for upper-scale glass and all main-scale glasses. The results show that the time to reach to optimal state reduced effectively. So that, if the starting temperature without using renormalization process is
is the actual minimum of the energy function. As temperature rises, glass energy also changes and the probability of reaching ground state is expected to gradually decrease. However, this drop is delayed until phase transition, where a sudden drop occurs. After phase transition temperature (critical temperature), the probability of reaching ground state decreases significantly. As shown in Fig. (8), this temperature is approximately 5.8* 10-5 for all of the five mentioned stocks. At this temperature, system is not in ground state and selecting any state as answer of the problem is unlikely to be a ground state.After the spin glass was placed in phase transition condition, renormalization process is performed. In this case, the glass is divided into several smaller glasses. Also according to formulas (2) and (3), a upper-glass scale is produced. Now, SA algorithm applies for upper-scale glass and all main-scale glasses. The results show that the time to reach to optimal state reduced effectively. So that, if the starting temperature without using renormalization process is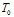 , then temperature, for the case with using renormalization process is approximately
, then temperature, for the case with using renormalization process is approximately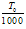 .This means, the SA algorithm needs lower temperature for initializing and is caused increasing convergence speed of the algorithm.Table (1), shows the time of convergence speed to finding spin glass ground state for two SA and SAMS algorithm. As shown, productivity (the ratio of the time of finding ground state that initialize with applying SAMS algorithm to the time of finding ground state with random initializing) is significant. For example, in Hang Seng stock market, productivity is 0.81 percent.In this experiment, the scale factor is 0.5 and glass is divided into two separated glasses.This experiment shows that dividing glasses into two separated glass cause higher convergence speed in finding its ground state but it may not find the ground state of the main glass respectively. However, the upper-scale glass ground state help to provide better initialization condition.Advantages in using this algorithm can be expressed as follows: 1) Initializing glass with one thousandth of original temperature means higher convergence speed and savings in time and energy. 2) Many of inappropriate states that were searched by SA, was not explored by SAMS; because of exploiting in the range of optimal state. 3) Provides possibility of using parallel processing for each glass separately. 4) If the bond energy between spins is weak then the SAMS algorithm gives better response. This is because, loosely interaction between spins, as expressed in [7], increase the local behavior of each spin and causes the local search methods, have greater accuracy to find the optimal states.
.This means, the SA algorithm needs lower temperature for initializing and is caused increasing convergence speed of the algorithm.Table (1), shows the time of convergence speed to finding spin glass ground state for two SA and SAMS algorithm. As shown, productivity (the ratio of the time of finding ground state that initialize with applying SAMS algorithm to the time of finding ground state with random initializing) is significant. For example, in Hang Seng stock market, productivity is 0.81 percent.In this experiment, the scale factor is 0.5 and glass is divided into two separated glasses.This experiment shows that dividing glasses into two separated glass cause higher convergence speed in finding its ground state but it may not find the ground state of the main glass respectively. However, the upper-scale glass ground state help to provide better initialization condition.Advantages in using this algorithm can be expressed as follows: 1) Initializing glass with one thousandth of original temperature means higher convergence speed and savings in time and energy. 2) Many of inappropriate states that were searched by SA, was not explored by SAMS; because of exploiting in the range of optimal state. 3) Provides possibility of using parallel processing for each glass separately. 4) If the bond energy between spins is weak then the SAMS algorithm gives better response. This is because, loosely interaction between spins, as expressed in [7], increase the local behavior of each spin and causes the local search methods, have greater accuracy to find the optimal states.7. Summary and Conclusions
- In this article, a new optimization algorithm (SAMS) for solving problems based on spin glasses is presented. This algorithm, by using multi-scaling property of material, tries to break problem into smaller problems. Since scaling can not be done at any condition, Kadanoff's theory has been used to show the best conditions of scaling. Based on Kadanoff's theory, the best condition of scaling is in phase transition condition at critical temperature of material. So, this algorithm uses these two properties and solves the portfolio selection problem as case study. The experiments show, this algorithm, in addition to confirm Kadanoff's theory in application, has more convergence speed than traditional methods such as SA and also, provides possibility of using parallel processing in optimization problems.
References
| [1] | Y. Bar-Yam, "About Enginerring Complex Systems: Multiscale Analysis and Evolutionary Engineering," Spiringer Verlag Berlin Heidelberg, pp: 16-31, (2005). |
| [2] | Y. Bar-Yam, Yaneer, "Dynamics of Complex Systems," Addison Wesley Longman, Inc., pp: 146-180, (1997). |
| [3] | D. Braha, Y. Bar-Yam "Topology of large-scale engineering problem-solving networks," Physical Review E, Vol. 69, 016113 (2004). |
| [4] | D.P. Landau, K. Binder, "A Guide to Monte Carlo Simulations in Statistical Physics," Second Edition, Cambridge University Press, pp: 1-45 (2000). |
| [5] | A. K. Hartmann, H. Rieger, "Optimization Algorithms in Physics," Wiley-VCH Verlag Co, pp: 46-121, (2002). |
| [6] | J.Z. Justin, "Phase Transitions and Renormalization Group," Oxford University Press, pp: 79-92, (2007). |
| [7] | J,Hasty, K. Wiesenfeld, "Renormalization of self-organized critical models," Annals of the New York Academy of Sciences, Issue Long-range correlations in Astrophysical Systems,Vol. 848, pp:9–17, (1998). |
| [8] | M.E. Fisher, "Renormalization group theory: its basis and formulation in statistical physics," Reviews of Modern Physics, Vol. 70, No. 2, (1988). |
| [9] | J. Houdayer and O.C. Martin, "Hierarchical approach for computing spin glass ground states," Physical Review E, Vol. 64, 056704, (2001). |
| [10] | M.Vafaei Jahan, M.R. Akabazadeh-T, "From Local Search to Global Conclusions: Migrating Spin Glass-based Distributed Portfolio Selection," IEEE transaction on Evolutionary Computation, No. 14, Issue 4, pp:591-601, (2010). |
| [11] | N. Kawashima, "Optimizataion Algorithms based on Renormalization Group," Progress of Theoretical Physics Supplement, Vol. 138; pp. 448-453(2000). |
| [12] | E.Bolthausen, A.Bovier, "Spin Glasses," Springer-Verlag Berlin Heidelberg, pp: 17-49, (2007). |
| [13] | H. Markowitz, "Portfolio Selection," Journal of Finance, No 7:77-91, (1952). |
| [14] | Ran El-Yaniv, "Competitive Solutions for Online Financial Problems," ACM computing Surveys, Vol. 30, No. 1, March (1998). |
| [15] | L. Ingber, "Simulated Annealing: Practice versus Theory," Mathematical Computer Modeling, Vol. 18, No. 11, Dec (1993). |
| [16] | Y. Crama, M. Schyns, "Simulated Annealing for Complex Portfolio Selection Problems," European Journal of Operational Research 150, pp: 546-571, (2003). |
| [17] | Portfolio selection benchmark data at "http://people.brunel.ac.uk/~mastjjb/jeb/orlib/portinfo.html" |
| [18] | A. K. Hartmann, M. Weigt, "Phase Transitions in Combinatorial Optimization Problems, Basics, Algorithms and Statistical Mechanics," Wiley-VCH Verlag Co, pp: 1-91 (2005). |
| [19] | D.Coppersmith, D.Gamarnik, M.Hajiaghayi, G.B. Sorkin, "Random max sat, Random max cut, and Their Phase Transitions," Journal of Random Structures and Algorithms, Vol. 24, Issue 4,pp:502-545, (2003). |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML