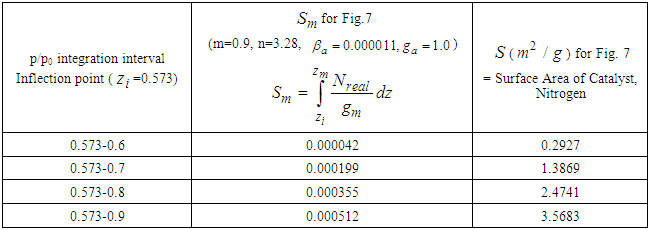Daekyoum Kim
Kwongmyoung-si Neobudae-ro, 32 Beon-kil, South Korea
Correspondence to: Daekyoum Kim, Kwongmyoung-si Neobudae-ro, 32 Beon-kil, South Korea.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
During studying the heat capacity of metals and brightening more than the original Lena’s image, we realize that the temperature increasing term obtained binomial expansion is used in the adsorption increasing term 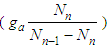 and we could derive the total adsorption isotherm equation with it. In the first layer the quantization does not occur and from
and we could derive the total adsorption isotherm equation with it. In the first layer the quantization does not occur and from  to
to  layer the quantization occurs. So as to get the total adsorption isotherm equation we add the quantized terms of the second to
layer the quantization occurs. So as to get the total adsorption isotherm equation we add the quantized terms of the second to 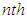 layers to the non-quantized term of the first layer. All terms are based on the unit surface sites. Hence the adsorption equations are derived much better than BET equation. The surface area is calculated through the integration of the adsorption isotherm equation from the inflection point to the wanted relative pressure.
layers to the non-quantized term of the first layer. All terms are based on the unit surface sites. Hence the adsorption equations are derived much better than BET equation. The surface area is calculated through the integration of the adsorption isotherm equation from the inflection point to the wanted relative pressure.
Keywords:
Refined BET, Binomial, Transforming, Adsorption Increasing Term, Surface Area, Inflection Point
Cite this paper: Daekyoum Kim, Better Refined Adsorption Isotherm than BET Equation, Advances in Analytical Chemistry, Vol. 7 No. 1, 2017, pp. 13-21. doi: 10.5923/j.aac.20170701.03.
1. Introduction
We derived the heat capacity equations of metals and then used consistent step multiplication of the appropriate binomial equations [1]. They are fitted to experimental data well [2]. The heat capacity equation (type V) and the adsorption equation (type II) draw sigmoid (S character) lines all together. And they are symmetry each other. The measurement gas of heat capacity is hydrogen or helium. The adsorption gases are water or nitrogen. The movements of their measurement gases are different. The former is expansion and the later contraction. The most important term in the derivation of heat capacity equation was the temperature increasing term, 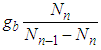 . In case of adsorption it becomes
. In case of adsorption it becomes 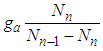 of the same form. Here
of the same form. Here 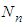 and
and 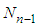 are the total molecules at the layers of
are the total molecules at the layers of 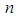 and
and 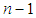 . Let us put
. Let us put 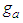 which is unit
which is unit 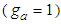 in data fitting as the constant. It is a testing constant. If
in data fitting as the constant. It is a testing constant. If 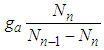 is transformed into
is transformed into 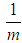 power of
power of 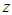 in every derivation of adsorption such as
in every derivation of adsorption such as 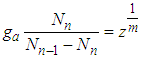 [3], the more advanced adsorption equation than BET eq. comes out.
[3], the more advanced adsorption equation than BET eq. comes out.
2. Statistical Modeling of Adsorption Isotherm
Suppose each level has one binomial equation for excitation and non-excitation. And suppose 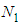 molecules are excited on
molecules are excited on 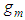 localized sites of the unit surface layer and
localized sites of the unit surface layer and 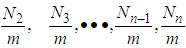 molecules on
molecules on 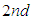 to
to  sites of the layers in sequence. Here m means quantization. The first adsorption layer has
sites of the layers in sequence. Here m means quantization. The first adsorption layer has 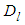 adsorption energy and. the second to
adsorption energy and. the second to 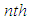 layer
layer 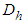 . Hence the adsorption probability over the first layer is
. Hence the adsorption probability over the first layer is 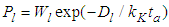 and the non-adsorption probability
and the non-adsorption probability 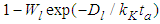 . In the above
. In the above 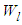 is the adsorption constant of the first adsorption layer.
is the adsorption constant of the first adsorption layer. 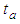 is similar to
is similar to 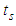 in heat capacity equation. The adsorption constant,
in heat capacity equation. The adsorption constant, 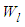 is calculable quantity. It is the expression to combine the rotation and vibration energy of the adsorbed molecules in the first layer.
is calculable quantity. It is the expression to combine the rotation and vibration energy of the adsorbed molecules in the first layer. 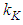 [2] is similar to
[2] is similar to 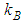 (Boltzmann’s constant). In the combination calculation of the first layer
(Boltzmann’s constant). In the combination calculation of the first layer 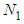 can take the values of from 0 to
can take the values of from 0 to 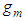 as variables in sequence. Then the binomial equation of the first layer becomes [1]
as variables in sequence. Then the binomial equation of the first layer becomes [1]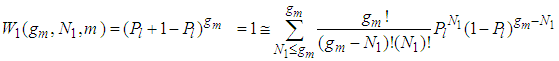 | (1) |
Next the adsorption probability of 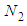 to
to 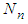 layers is
layers is 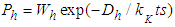 and then the non-adsorption probability
and then the non-adsorption probability 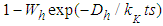 . The constants of these are the same as those of
. The constants of these are the same as those of 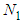 layer in the above. The binomial expansion equations for
layer in the above. The binomial expansion equations for 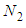 to
to 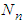 layers are
layers are 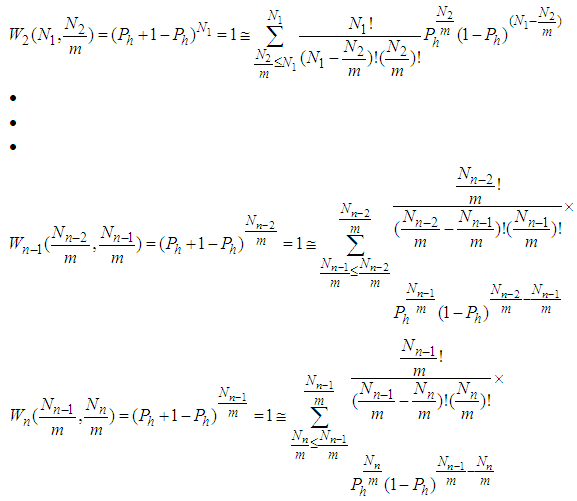 | (2) |
Let us multiply (1) and (2) side by side. Then for 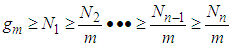
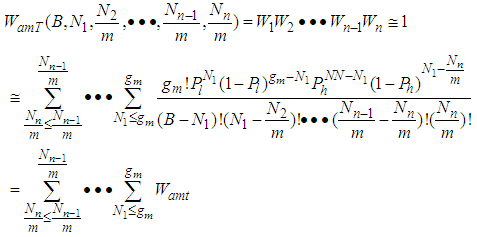 | (3) |
In the above 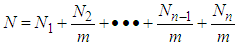 | (3.1) |
In Eq. (3) the largest term dominates the equation. So the total differential of Eq. (3) becomes the zero which requires that the coefficients of all terms should be zero. Hence by using Stirling’s approximation we solve the equation, 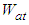 . The first differential equation of Eq (3) becomes
. The first differential equation of Eq (3) becomes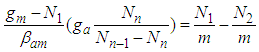 | (4) |
In the above equations m is quantization constant. In the reference [4] m value should be corrected as those in the present figure [Fig. 1]. The constants have three parts of 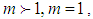
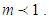 As we see in Fig. 1, bonding constant mean quantization. If
As we see in Fig. 1, bonding constant mean quantization. If 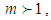 bonding occurs in many directions. If
bonding occurs in many directions. If 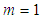 no quantization occur and if
no quantization occur and if  the adsorptions are interrupted in many directions. In Eq. (4)
the adsorptions are interrupted in many directions. In Eq. (4)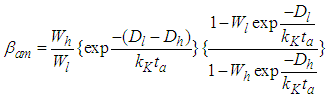 | (4.1) |
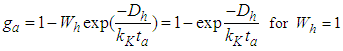 | (4.2) |
It is possible that  is put as unit.The next equations are
is put as unit.The next equations are 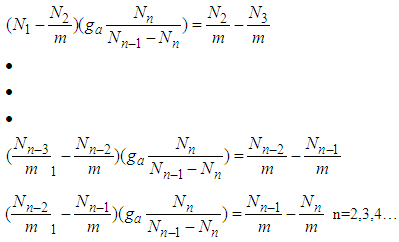 | (5) |
In Eqs (4) and (5) let us put 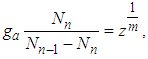 then
then 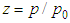 which is same as Eq. (9) of the reference [5] solved by using the chemical potential
which is same as Eq. (9) of the reference [5] solved by using the chemical potential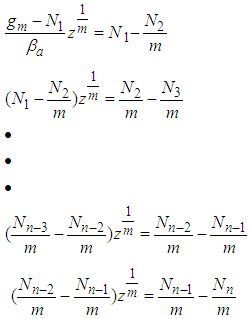 | (6) |
In Eq. (6) add side by side and rearrange 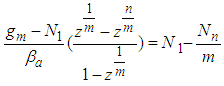 | (7) |
In Eq. (6) multiple side by side and rearrange 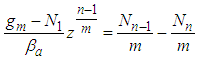 | (8) |
We solve Eq. (8) with 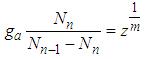 in order to eliminate
in order to eliminate 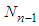
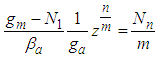 | (9) |
We solve Eq. (7) with Eq. (9) in order to eliminate 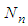
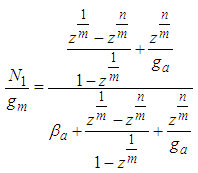 | (10) |
Eq. (10) represents the adsorption amount of the first layer. It is Langmuir equation. The quantization values (m) and the numbers of the adsorption layer (n) are influential on the determination of 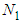 . All values of the parameters
. All values of the parameters 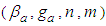 directly participate in the determination of
directly participate in the determination of 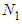 and following
and following 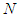 . The value of
. The value of 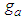 is much influential on the determination of the last term (
is much influential on the determination of the last term (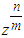 ). But it does not much increase or decrease of
). But it does not much increase or decrease of 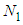 since it exists in the denominator and nominator. At
since it exists in the denominator and nominator. At 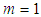 it becomes
it becomes 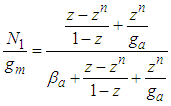 | (11) |
Therefore the total adsorption amount per unit surface  that is, the adsorption isotherm for from first layer to the last (n) layer becomes by using Eqs (6) and (10) as follows
that is, the adsorption isotherm for from first layer to the last (n) layer becomes by using Eqs (6) and (10) as follows 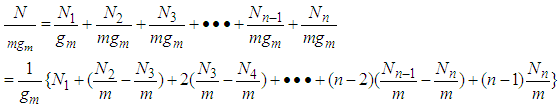 | (12) |
If 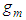 is eliminated in Eq (12)
is eliminated in Eq (12) 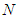 becomes as follows
becomes as follows 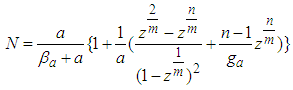 | (12.1) |
If 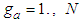 is a linear function of four variables. In the above
is a linear function of four variables. In the above 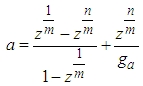 | (12.2) |
And the total adsorption rate is a linear function of z made of four constants 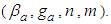 The equation draws BET-like lines and fits BET type experimental data well. At
The equation draws BET-like lines and fits BET type experimental data well. At  it becomes
it becomes 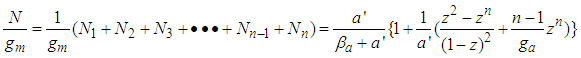 | (13) |
In the above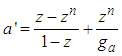 | (13.1) |
If the measurement gas is nitrogen, the general empirical formulae, 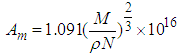 is introduced into.
is introduced into. 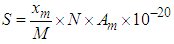 to get the specific surface area of the adsorbent,
to get the specific surface area of the adsorbent, 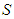 [6]. Then
[6]. Then 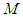 is the molecular weight of nitrogen and
is the molecular weight of nitrogen and 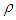 density of nitrogen and
density of nitrogen and 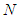 Avogadro number, Hence from empirical formulae
Avogadro number, Hence from empirical formulae 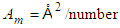 is used. The monolayer capacity,
is used. The monolayer capacity, 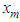 should also be substituted by the value of the integration of Eq. (12) subtracted by the surface adsorption isotherm
should also be substituted by the value of the integration of Eq. (12) subtracted by the surface adsorption isotherm 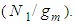
3. Result and Discussion
The base of Eq. (10) and Eq. (12) is 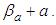 So we may use the word, the rate without the dimensionless analysis. It affects the equation totally. Fig. 2 shows the total adsorption rate according to the values of
So we may use the word, the rate without the dimensionless analysis. It affects the equation totally. Fig. 2 shows the total adsorption rate according to the values of 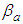 . In accordance with the values of z approaching units, the total adsorption rates approach closely with one another. This seems to mean that the adsorption heat of the first layer is same as those of
. In accordance with the values of z approaching units, the total adsorption rates approach closely with one another. This seems to mean that the adsorption heat of the first layer is same as those of 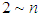 layers. We call m the quantization values. It seems to have same notion as the quantization appears in quantum mechanism. We are dealing statistical quantization which should exist in statistics. We can differentiate them, three cases.
layers. We call m the quantization values. It seems to have same notion as the quantization appears in quantum mechanism. We are dealing statistical quantization which should exist in statistics. We can differentiate them, three cases. 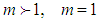 and
and 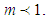 The cases of
The cases of 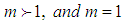 explain bonding and
explain bonding and 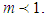 explains existence of the interruptions for bonding. Fig 3 explains the increase of the adsorption rate according to m values. Less m than unit seem to interrupt the bonding. Fig. 4 represents the total adsorption rates according to n values. At less z than 0.5 the isotherms show the same adsorption rates. The constant
explains existence of the interruptions for bonding. Fig 3 explains the increase of the adsorption rate according to m values. Less m than unit seem to interrupt the bonding. Fig. 4 represents the total adsorption rates according to n values. At less z than 0.5 the isotherms show the same adsorption rates. The constant 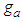 showed in Fig 5 should be positive. When
showed in Fig 5 should be positive. When 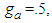 the constants draw the type II isotherm. At
the constants draw the type II isotherm. At 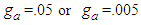 the same types of the isotherm appear.
the same types of the isotherm appear. 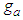 can include greater values than or equal unit.
can include greater values than or equal unit. 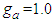 seems to be best. Fig. 6 shows
seems to be best. Fig. 6 shows 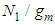 with respect to the relative pressure like Langmuir’s lines which can’t become unit even if a is very large or
with respect to the relative pressure like Langmuir’s lines which can’t become unit even if a is very large or 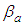 much smaller. The parameter values of Fig. 2 come from the following Fig. 7 and Fig. 8. According to the above variations we optimized two kinds of the experimental adsorption data showed in Figs. 7 [6] and 8 [7] using trial and error method. The experimental data of Fig. 7 are obtained from the Figure 2-10 of the reference [6]. The experimental data are fitted to Eq. (12) well. As we see in Figs 7 and 8, BET isotherm can’t imitate the experimental data except for beginning. What is the catalyst? As we see Fig. 9 in the above, 1, 2, 3, 4, 5, 6 and 7 molecules can function as the catalyst. That is, the molecules of the surface adsorption layer can’t function like the catalyst. Because they use much energy in order to hold the surface. So they are not active. The molecules which lie on the surface layer adsorption molecules which hold the surface, can function as the real catalyst. Therefore in Eq. (12),
much smaller. The parameter values of Fig. 2 come from the following Fig. 7 and Fig. 8. According to the above variations we optimized two kinds of the experimental adsorption data showed in Figs. 7 [6] and 8 [7] using trial and error method. The experimental data of Fig. 7 are obtained from the Figure 2-10 of the reference [6]. The experimental data are fitted to Eq. (12) well. As we see in Figs 7 and 8, BET isotherm can’t imitate the experimental data except for beginning. What is the catalyst? As we see Fig. 9 in the above, 1, 2, 3, 4, 5, 6 and 7 molecules can function as the catalyst. That is, the molecules of the surface adsorption layer can’t function like the catalyst. Because they use much energy in order to hold the surface. So they are not active. The molecules which lie on the surface layer adsorption molecules which hold the surface, can function as the real catalyst. Therefore in Eq. (12), 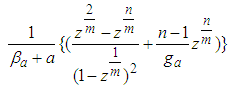 part must work in the catalytic reaction. Hence the real adsorption equation becomes
part must work in the catalytic reaction. Hence the real adsorption equation becomes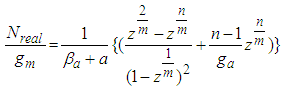 | (14) |
If this equation is integrated from the inflection point 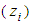 to each optional relative pressure
to each optional relative pressure 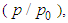 we get the mono-area capacity
we get the mono-area capacity 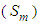 with respect to the relative pressure (p/p0). Tables 1 and 2 include those. Then the surface area for the catalyst obtained from the equation becomes
with respect to the relative pressure (p/p0). Tables 1 and 2 include those. Then the surface area for the catalyst obtained from the equation becomes 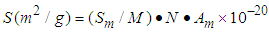 with
with 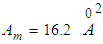 per number for nitrogen and
per number for nitrogen and  per number for water (Table 2) [6] by substituting
per number for water (Table 2) [6] by substituting 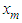 . in the equation of (2.60) of the reference [6] by
. in the equation of (2.60) of the reference [6] by 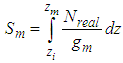 in which
in which 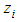 =inflection point and
=inflection point and 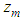 =optional z value after the inflection point. In the above equation
=optional z value after the inflection point. In the above equation 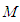 is the molecular weight (g) per g-mole and
is the molecular weight (g) per g-mole and 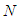 Avogadro number per g-mole.
Avogadro number per g-mole.Table 1. Sm (mono-area capacity) and S (surface area) for Fig. 7
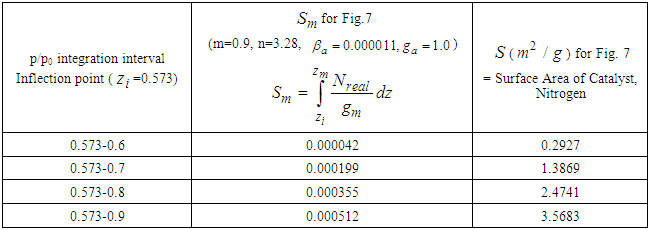 |
| |
|
Table 2. Sm (mono-area capacity) and S (surface area) for Fig. 8
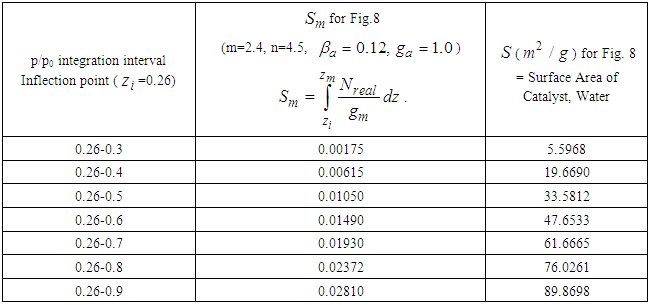 |
| |
|
Then the inflection points are obtained by Secant method [8] through the program showed in Appendix 1. Specific surface areas are changed according to the optional relative pressures. These are showed in Tables 1 and 2 precisely. The integrations with respect to z surface values give the total adsorption site numbers of the adsorbate. Before the inflection point the specific surface area of the adsorbent is not counted as a catalyst since it makes the strong surface film [9]. The adsorption rate increases consistently after the inflection point. The values of n of Fig. 7 and Fig. 8 match the range of the reference of BET [10]. The completion of 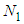 to unit goes with the completion of N to the end as we see in Fig. 6 and its equation. But from the inflection point the pilling up of
to unit goes with the completion of N to the end as we see in Fig. 6 and its equation. But from the inflection point the pilling up of 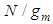 may begin characteristically. Eq. (13) can be used in the data fitting with
may begin characteristically. Eq. (13) can be used in the data fitting with 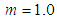 and
and 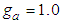 . Its quality is poor.Our study have realized the saying that “After considerable work on the theory, Hill (1946) formed the opinion that any future improvement on it must be in the form of refinement rather than a modification on the basic theory” [11, 12].
. Its quality is poor.Our study have realized the saying that “After considerable work on the theory, Hill (1946) formed the opinion that any future improvement on it must be in the form of refinement rather than a modification on the basic theory” [11, 12].
4. Conclusions
The total adsorption rate equations closely related with the past references are derived correctly and the figures according to four constants 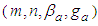 are also considered to describe BET-like figures (II) well. The quantization constants are useful in deriving the adsorption equations. In order to calculate the surface area of the catalysts the total adsorption equations excluding the first layer adsorption equation and their inflection points obtained are used appropriately. They fit the experimental data well.
are also considered to describe BET-like figures (II) well. The quantization constants are useful in deriving the adsorption equations. In order to calculate the surface area of the catalysts the total adsorption equations excluding the first layer adsorption equation and their inflection points obtained are used appropriately. They fit the experimental data well.
ACKNOWLEDGEMENTS
The author thanks for the challenging encouragements of Yongduk Kim, an emeritus professor of Sogang University. And the author thanks for helping the manuscript arrangement of Jones Cathy (http://www.sapub.org/), USA.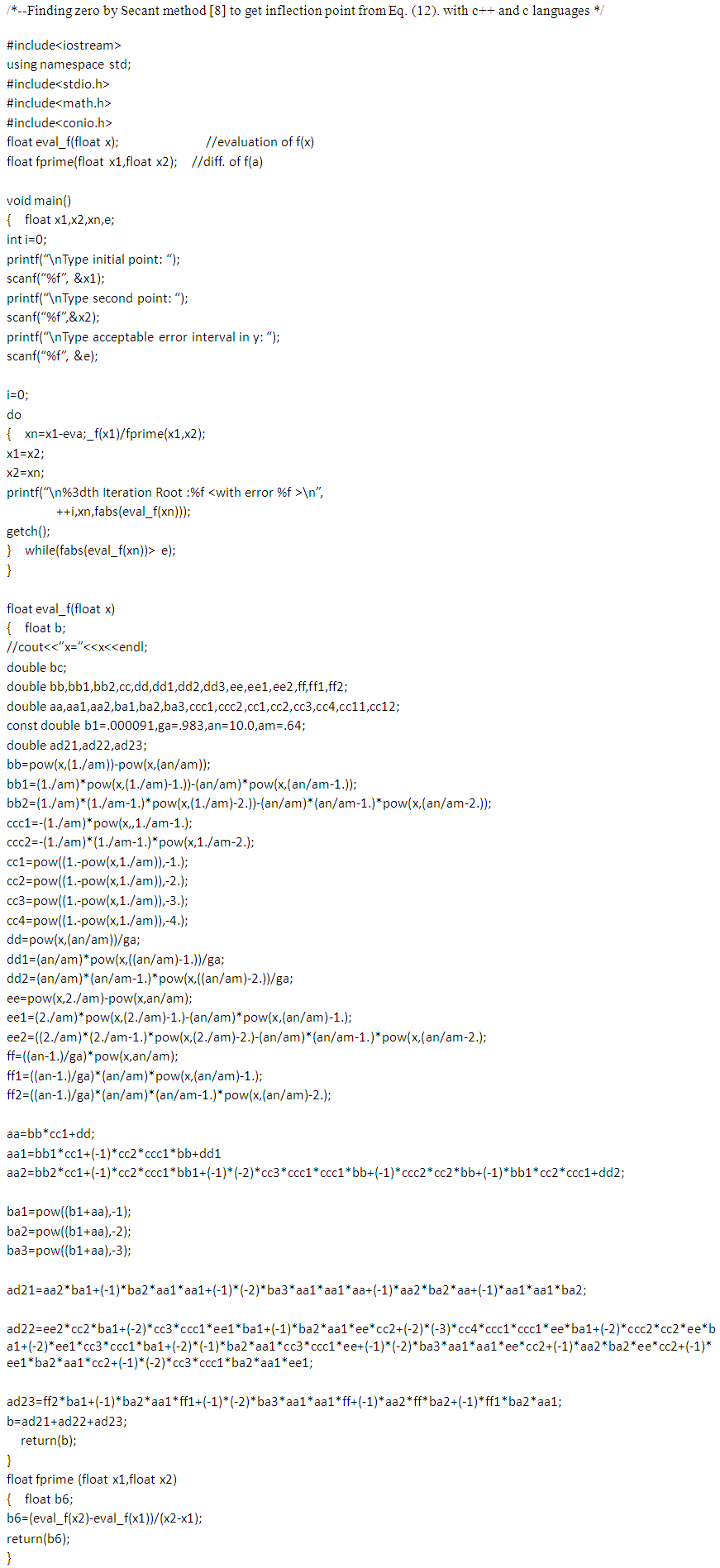 | Appendix 1 |
References
| [1] | F. Reif, Fundamentals of statistical and thermal physics, (McGraw-Hill Inc Ed. 1965), Chapter 1. pp. 10-46 (2015). |
| [2] | Kim D. et. al, New Physics: Sae Mulli (The Korean Physical Society), Volume 60, Number 7, pp 729(2010). |
| [3] | John H. Mathews and Russell W. Howell, Complex Analysis for Mathematics and Engineering, 4th ed., Jones and Bartlett Publishers, Inc., pp 62 (2001). |
| [4] | Kim D., Korean J. of Chem. Eng. 17(5), pp 600 (2000). |
| [5] | Kim D. and Choi Y. S. New Physics: Sae Mulli (The Korean Physical Society), Volume 61, Number 3, pp 248 (2011). |
| [6] | Gregg, S. J. and Sing, K. S. W., Adorption, Surface area and Porosity, Academic Press Inc.(Ltd.), Chapter 2, pp 53 (1969). |
| [7] | Benson R. Sundheim, M onroe H. Waxman and Harry P. Gregor, J Phys Chem. Vol. 57, pp 974 (1953). |
| [8] | C-ro- guhyouhan Numerical Analysis(Korean Language), Ji, Youngjun, Kim, Hoajun, and Heo Jeongguin, Nopi-gipi publishing Company pp. 24 (2002). |
| [9] | George Jura and William D. Harkins, J. Amer. Chem. Soc. 67, 1356(1944). |
| [10] | Stephen Brunauer, P. H. Emmett and Edward Teller, J. of Amer. Chem. Soc., Vol > 90, pp. 309 (1938). |
| [11] | Caurie, M., J. Food Sci (The Year after 1979). |
| [12] | Caurie, M., J. Food Sci. (the year after 1979), 63. |



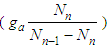 and we could derive the total adsorption isotherm equation with it. In the first layer the quantization does not occur and from
and we could derive the total adsorption isotherm equation with it. In the first layer the quantization does not occur and from 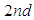 to
to 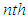 layer the quantization occurs. So as to get the total adsorption isotherm equation we add the quantized terms of the second to
layer the quantization occurs. So as to get the total adsorption isotherm equation we add the quantized terms of the second to 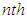 layers to the non-quantized term of the first layer. All terms are based on the unit surface sites. Hence the adsorption equations are derived much better than BET equation. The surface area is calculated through the integration of the adsorption isotherm equation from the inflection point to the wanted relative pressure.
layers to the non-quantized term of the first layer. All terms are based on the unit surface sites. Hence the adsorption equations are derived much better than BET equation. The surface area is calculated through the integration of the adsorption isotherm equation from the inflection point to the wanted relative pressure.
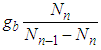 . In case of adsorption it becomes
. In case of adsorption it becomes 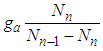 of the same form. Here
of the same form. Here 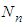 and
and 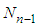 are the total molecules at the layers of
are the total molecules at the layers of 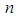 and
and 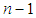 . Let us put
. Let us put 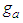 which is unit
which is unit 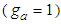 in data fitting as the constant. It is a testing constant. If
in data fitting as the constant. It is a testing constant. If 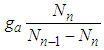 is transformed into
is transformed into 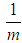 power of
power of 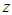 in every derivation of adsorption such as
in every derivation of adsorption such as 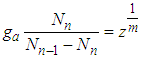 [3], the more advanced adsorption equation than BET eq. comes out.
[3], the more advanced adsorption equation than BET eq. comes out. 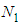 molecules are excited on
molecules are excited on 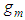 localized sites of the unit surface layer and
localized sites of the unit surface layer and 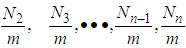 molecules on
molecules on 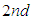 to
to  sites of the layers in sequence. Here m means quantization. The first adsorption layer has
sites of the layers in sequence. Here m means quantization. The first adsorption layer has 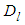 adsorption energy and. the second to
adsorption energy and. the second to 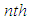 layer
layer 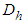 . Hence the adsorption probability over the first layer is
. Hence the adsorption probability over the first layer is 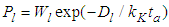 and the non-adsorption probability
and the non-adsorption probability 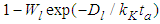 . In the above
. In the above 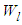 is the adsorption constant of the first adsorption layer.
is the adsorption constant of the first adsorption layer. 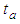 is similar to
is similar to 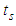 in heat capacity equation. The adsorption constant,
in heat capacity equation. The adsorption constant, 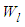 is calculable quantity. It is the expression to combine the rotation and vibration energy of the adsorbed molecules in the first layer.
is calculable quantity. It is the expression to combine the rotation and vibration energy of the adsorbed molecules in the first layer. 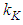 [2] is similar to
[2] is similar to 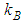 (Boltzmann’s constant). In the combination calculation of the first layer
(Boltzmann’s constant). In the combination calculation of the first layer 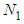 can take the values of from 0 to
can take the values of from 0 to 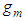 as variables in sequence. Then the binomial equation of the first layer becomes [1]
as variables in sequence. Then the binomial equation of the first layer becomes [1]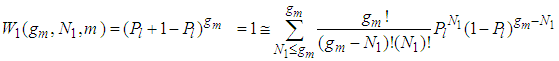
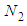 to
to 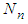 layers is
layers is 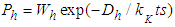 and then the non-adsorption probability
and then the non-adsorption probability 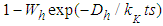 . The constants of these are the same as those of
. The constants of these are the same as those of  layer in the above. The binomial expansion equations for
layer in the above. The binomial expansion equations for  to
to 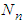 layers are
layers are 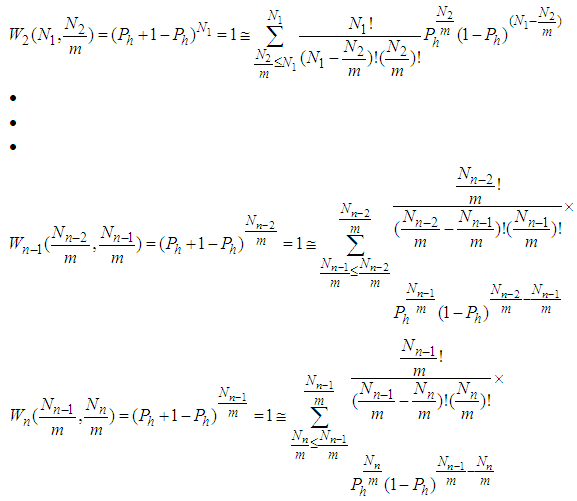
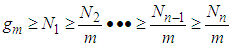
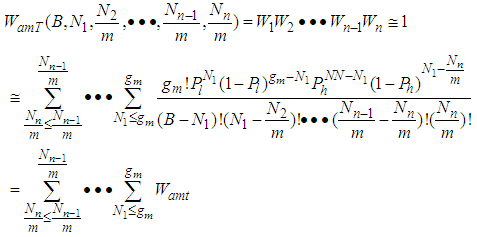
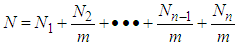
 . The first differential equation of Eq (3) becomes
. The first differential equation of Eq (3) becomes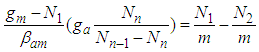
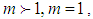
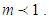 As we see in Fig. 1, bonding constant mean quantization. If
As we see in Fig. 1, bonding constant mean quantization. If 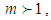 bonding occurs in many directions. If
bonding occurs in many directions. If 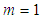 no quantization occur and if
no quantization occur and if  the adsorptions are interrupted in many directions. In Eq. (4)
the adsorptions are interrupted in many directions. In Eq. (4)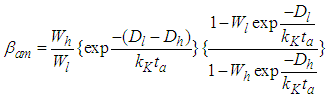
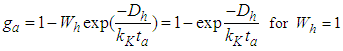
 is put as unit.The next equations are
is put as unit.The next equations are 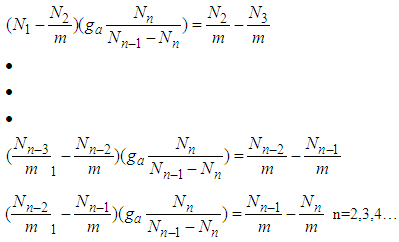
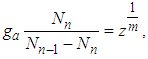 then
then 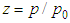 which is same as Eq. (9) of the reference [5] solved by using the chemical potential
which is same as Eq. (9) of the reference [5] solved by using the chemical potential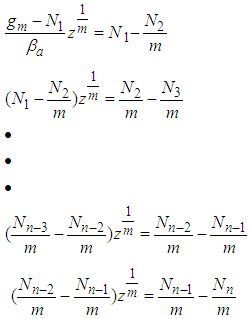
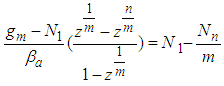
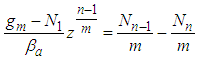
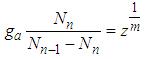 in order to eliminate
in order to eliminate 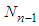
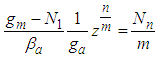
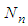
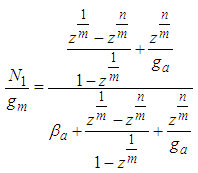
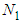 . All values of the parameters
. All values of the parameters 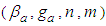 directly participate in the determination of
directly participate in the determination of 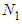 and following
and following 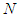 . The value of
. The value of 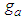 is much influential on the determination of the last term (
is much influential on the determination of the last term (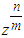 ). But it does not much increase or decrease of
). But it does not much increase or decrease of 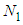 since it exists in the denominator and nominator. At
since it exists in the denominator and nominator. At 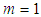 it becomes
it becomes 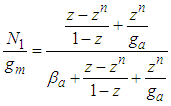
 that is, the adsorption isotherm for from first layer to the last (n) layer becomes by using Eqs (6) and (10) as follows
that is, the adsorption isotherm for from first layer to the last (n) layer becomes by using Eqs (6) and (10) as follows 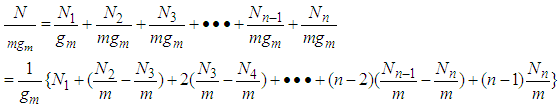
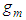 is eliminated in Eq (12)
is eliminated in Eq (12) 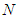 becomes as follows
becomes as follows 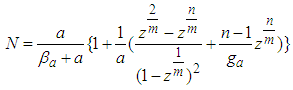
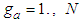 is a linear function of four variables. In the above
is a linear function of four variables. In the above 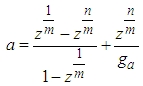
 The equation draws BET-like lines and fits BET type experimental data well. At
The equation draws BET-like lines and fits BET type experimental data well. At 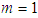 it becomes
it becomes 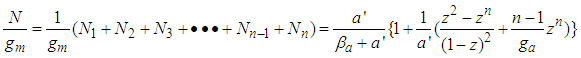
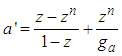
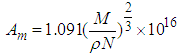 is introduced into.
is introduced into. 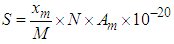 to get the specific surface area of the adsorbent,
to get the specific surface area of the adsorbent, 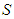 [6]. Then
[6]. Then 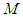 is the molecular weight of nitrogen and
is the molecular weight of nitrogen and 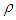 density of nitrogen and
density of nitrogen and 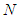 Avogadro number, Hence from empirical formulae
Avogadro number, Hence from empirical formulae 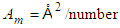 is used. The monolayer capacity,
is used. The monolayer capacity, 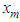 should also be substituted by the value of the integration of Eq. (12) subtracted by the surface adsorption isotherm
should also be substituted by the value of the integration of Eq. (12) subtracted by the surface adsorption isotherm 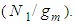
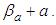 So we may use the word, the rate without the dimensionless analysis. It affects the equation totally. Fig. 2 shows the total adsorption rate according to the values of
So we may use the word, the rate without the dimensionless analysis. It affects the equation totally. Fig. 2 shows the total adsorption rate according to the values of 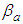 . In accordance with the values of z approaching units, the total adsorption rates approach closely with one another. This seems to mean that the adsorption heat of the first layer is same as those of
. In accordance with the values of z approaching units, the total adsorption rates approach closely with one another. This seems to mean that the adsorption heat of the first layer is same as those of 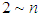 layers. We call m the quantization values. It seems to have same notion as the quantization appears in quantum mechanism. We are dealing statistical quantization which should exist in statistics. We can differentiate them, three cases.
layers. We call m the quantization values. It seems to have same notion as the quantization appears in quantum mechanism. We are dealing statistical quantization which should exist in statistics. We can differentiate them, three cases. 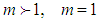 and
and 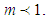 The cases of
The cases of 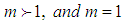 explain bonding and
explain bonding and 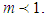 explains existence of the interruptions for bonding. Fig 3 explains the increase of the adsorption rate according to m values. Less m than unit seem to interrupt the bonding. Fig. 4 represents the total adsorption rates according to n values. At less z than 0.5 the isotherms show the same adsorption rates. The constant
explains existence of the interruptions for bonding. Fig 3 explains the increase of the adsorption rate according to m values. Less m than unit seem to interrupt the bonding. Fig. 4 represents the total adsorption rates according to n values. At less z than 0.5 the isotherms show the same adsorption rates. The constant 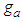 showed in Fig 5 should be positive. When
showed in Fig 5 should be positive. When 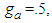 the constants draw the type II isotherm. At
the constants draw the type II isotherm. At 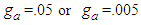 the same types of the isotherm appear.
the same types of the isotherm appear. 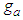 can include greater values than or equal unit.
can include greater values than or equal unit. 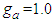 seems to be best. Fig. 6 shows
seems to be best. Fig. 6 shows 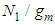 with respect to the relative pressure like Langmuir’s lines which can’t become unit even if a is very large or
with respect to the relative pressure like Langmuir’s lines which can’t become unit even if a is very large or 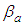 much smaller. The parameter values of Fig. 2 come from the following Fig. 7 and Fig. 8. According to the above variations we optimized two kinds of the experimental adsorption data showed in Figs. 7 [6] and 8 [7] using trial and error method. The experimental data of Fig. 7 are obtained from the Figure 2-10 of the reference [6]. The experimental data are fitted to Eq. (12) well. As we see in Figs 7 and 8, BET isotherm can’t imitate the experimental data except for beginning. What is the catalyst? As we see Fig. 9 in the above, 1, 2, 3, 4, 5, 6 and 7 molecules can function as the catalyst. That is, the molecules of the surface adsorption layer can’t function like the catalyst. Because they use much energy in order to hold the surface. So they are not active. The molecules which lie on the surface layer adsorption molecules which hold the surface, can function as the real catalyst. Therefore in Eq. (12),
much smaller. The parameter values of Fig. 2 come from the following Fig. 7 and Fig. 8. According to the above variations we optimized two kinds of the experimental adsorption data showed in Figs. 7 [6] and 8 [7] using trial and error method. The experimental data of Fig. 7 are obtained from the Figure 2-10 of the reference [6]. The experimental data are fitted to Eq. (12) well. As we see in Figs 7 and 8, BET isotherm can’t imitate the experimental data except for beginning. What is the catalyst? As we see Fig. 9 in the above, 1, 2, 3, 4, 5, 6 and 7 molecules can function as the catalyst. That is, the molecules of the surface adsorption layer can’t function like the catalyst. Because they use much energy in order to hold the surface. So they are not active. The molecules which lie on the surface layer adsorption molecules which hold the surface, can function as the real catalyst. Therefore in Eq. (12), 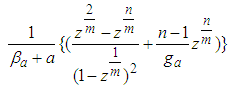 part must work in the catalytic reaction. Hence the real adsorption equation becomes
part must work in the catalytic reaction. Hence the real adsorption equation becomes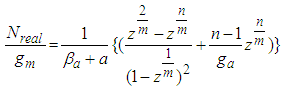
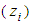 to each optional relative pressure
to each optional relative pressure 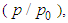 we get the mono-area capacity
we get the mono-area capacity 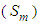 with respect to the relative pressure (p/p0). Tables 1 and 2 include those. Then the surface area for the catalyst obtained from the equation becomes
with respect to the relative pressure (p/p0). Tables 1 and 2 include those. Then the surface area for the catalyst obtained from the equation becomes 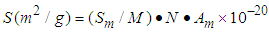 with
with 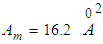 per number for nitrogen and
per number for nitrogen and  per number for water (Table 2) [6] by substituting
per number for water (Table 2) [6] by substituting 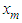 . in the equation of (2.60) of the reference [6] by
. in the equation of (2.60) of the reference [6] by 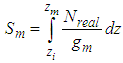 in which
in which 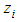 =inflection point and
=inflection point and 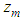 =optional z value after the inflection point. In the above equation
=optional z value after the inflection point. In the above equation 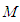 is the molecular weight (g) per g-mole and
is the molecular weight (g) per g-mole and 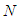 Avogadro number per g-mole.
Avogadro number per g-mole.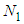 to unit goes with the completion of N to the end as we see in Fig. 6 and its equation. But from the inflection point the pilling up of
to unit goes with the completion of N to the end as we see in Fig. 6 and its equation. But from the inflection point the pilling up of 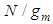 may begin characteristically. Eq. (13) can be used in the data fitting with
may begin characteristically. Eq. (13) can be used in the data fitting with 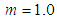 and
and 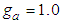 . Its quality is poor.Our study have realized the saying that “After considerable work on the theory, Hill (1946) formed the opinion that any future improvement on it must be in the form of refinement rather than a modification on the basic theory” [11, 12].
. Its quality is poor.Our study have realized the saying that “After considerable work on the theory, Hill (1946) formed the opinion that any future improvement on it must be in the form of refinement rather than a modification on the basic theory” [11, 12].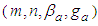 are also considered to describe BET-like figures (II) well. The quantization constants are useful in deriving the adsorption equations. In order to calculate the surface area of the catalysts the total adsorption equations excluding the first layer adsorption equation and their inflection points obtained are used appropriately. They fit the experimental data well.
are also considered to describe BET-like figures (II) well. The quantization constants are useful in deriving the adsorption equations. In order to calculate the surface area of the catalysts the total adsorption equations excluding the first layer adsorption equation and their inflection points obtained are used appropriately. They fit the experimental data well. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML