-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Advances in Analytical Chemistry
p-ISSN: 2163-2839 e-ISSN: 2163-2847
2013; 3(2): 9-14
doi:10.5923/j.aac.20130302.01
Estimation of Surface and Interface Roughness Using X-ray Reflectivity and TEM Observation
Yoshikazu Fujii
Kobe University, kobe 657-8501, Japan
Correspondence to: Yoshikazu Fujii, Kobe University, kobe 657-8501, Japan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Surface and interface roughness of multilayer surface are often estimated with using X-ray reflectivity (XRR). In the conventional XRR analysis, the reflectivity is calculated based on the Parratt formalism, accounting for the effect of roughness by the theory of Nevot-Croce. However, the calculated result showed a strange phenomenon. The strange result had its origin in a currently used an equation due to serious mistake in which the Fresnel transmission coefficient in the reflectivity equation was increased at a rough interface because of a lack of consideration of diffuse scattering. Then we have developed a new improved formalism that corrects this mistake. In this study, we present the applying of the new improved formalism with the use of TEM observation results. The new improved formalism derives a more accurate analysis of the x-ray reflectivity from a multilayer surface of thin film material.
Keywords: Surface , Interface Roughness, Multilayered Thin Film Materials, X-Ray Reflectivity
Cite this paper: Yoshikazu Fujii, Estimation of Surface and Interface Roughness Using X-ray Reflectivity and TEM Observation, Advances in Analytical Chemistry, Vol. 3 No. 2, 2013, pp. 9-14. doi: 10.5923/j.aac.20130302.01.
Article Outline
1. Introduction
- X-ray reflectivity (XRR) is a powerful tool for investigations on rough surface and interface structures of material surfaces as multilayered thin film[1-11]. In many previous XRR analysis, the X-ray reflectivity was calculated based on the Parratt formalism[1], coupled with the use of the theory of Nevot and Croce to include roughness[2]. However, the calculated results of the X-ray reflectivity done in this way often showed strange results where the amplitude of the oscillation due to the interference effects would increase for a rougher surface. And the estimation results of surface and interfacial roughness by x-ray reflectivity measurements did not correspond to those from transmission electron microscope (TEM) observation[6]. The origin of the strange behavior was attributed to the fact that the diffuse scattering at the rough interface was not correctly taken into account by Nevot and Croce[2]. Then we have developed a new formalism in which the effects of the surface and interface roughness are included correctly. The new improved formalism derives an accurate analysis of the x-ray reflectivity from a multilayer surface of thin film materials, taking into account the effect of roughness-induced diffuse scattering. In the new improved formulae for the x-ray reflectivity, the well known reduced Fresnel coefficients for reflection is applied to the Fresnel coefficients for reflection at rough interface. While an accurate analytical formula for the Fresnel coefficients for refraction at rough interface is not available. There are several approximations proposed so far and all these results can be written by including any parameters depend on the proposed approximations. In the present work, we tried to determine these parameters experimentally by comparing the results of the TEM observation and x-ray reflectivity.
2. Comparison between X-ray Reflectivity Measurement and TEM Observation
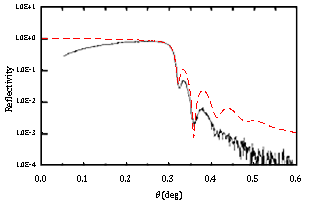
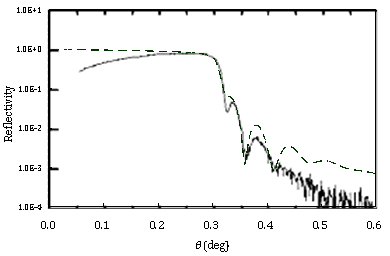
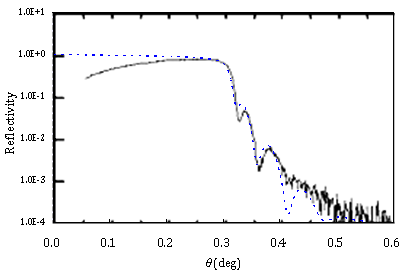
- The surface sample for examination was prepared as follows; a GaAs layer was grown on Si(110) by molecular beam epitaxy (MBE). From the TEM observations, the thickness of the GaAs layer was 48 nm, the root-mean-square (rms) roughness σ1 of the GaAs surface was about 4.3 nm, the rms roughness of the interface between GaAs and Si was about 0.7 nm. (We estimated σ1=2.8nm in the previous study, now we revise the σ1 in 4.3nm.) Figure 1 shows a cross section image of this GaAs / Si(110) sample observed by TEM.X-ray reflectivity measurements were performed using a Cu-Kα x-ray beam from an 18 kW rotating-anode source. In Figure 2, the solid line shows the measured x-ray reflectivity from the surface sample of the GaAs layer on the silicon wafer. The oscillations in decrease signal for angles larger than the total reflection critical angle are caused by interference between x-rays that reflect from the surface of GaAs layer and those that reflect from the interface of the GaAs layer and Si substrate. The characteristics of these oscillations reflect the surface roughness and the interface roughness.
 | Figure 1. Cross section image of GaAs / Si(110) by TEM observation |
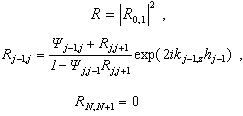 | (1) |
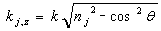 | (2) |
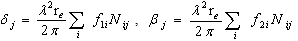 | (3) |
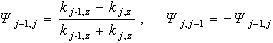 | (4) |
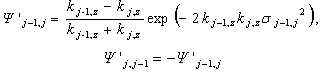 | (5) |
3. Improved Formalism of X-ray Reflectivity
- We have developed a new formula in which the effects of the surface and interface roughness are correctly treated. In the following, we show in detail the process of obtaining Parratt's expression and, further, show that this expression requires conservation of energy at the interface. We go on to show that the dispersion of the energy by interface roughness cannot be correctly accounted for Parratt's expression.In the first, we consider the reflection from a flat surface of a multilayer with flat interfaces. We take the vertical direction to the surface as the z axis, with the positive direction pointing towards the bulk. The scattering plane is made the x-z plane. Following that approach, let nj be the refractive index of the j-th layer. The electric field of x-ray radiation at a glancing angle of incidence θ is expressed as
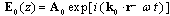 | (6) |
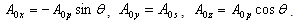 | (7) |
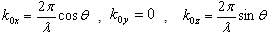 | (8) |
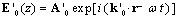 | (9) |
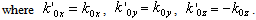 | (10) |
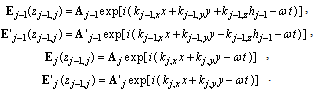 | (11) |
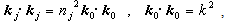 | (12) |
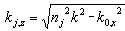 | (13) |
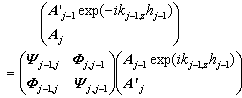 | (14) |
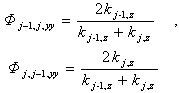 | (15) |
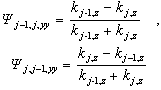 | (16) |
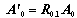 | (17) |
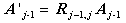 | (18) |
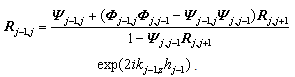 | (19) |
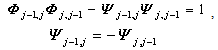 | (20) |
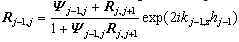 | (21) |
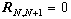 | (22) |
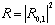 | (23) |
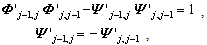 | (24) |
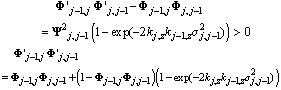 | (25) |
 | (26) |
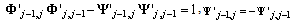 | (27) |
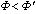 .The penetration of x-rays should decrease at a rough interface because of diffuse scattering. Therefore, the identity equation for the Fresnel coefficients should become,
.The penetration of x-rays should decrease at a rough interface because of diffuse scattering. Therefore, the identity equation for the Fresnel coefficients should become,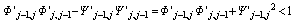 | (28) |
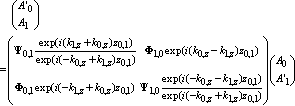 | (29) |
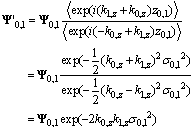 | (30) |
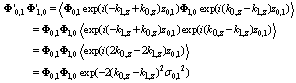 | (31) |
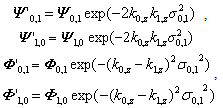 | (32) |
4. Conclusions
- We have developed a new improved formalism of x-ray reflectivity. In this study, we present the applying of the new improved formalism with the use of TEM observation results. In the new improved formulae for the x-ray reflectivity, an accurate analytical formula for the Fresnel coefficients for refraction at rough interface was not available. In this study, we show to be able to determine these parameters in the Fresnel coefficients for refraction experimentally by comparing the measurements of TEM observation results and x-ray reflectivity. It is thought that the value of these parameters depend on the structure of a parallel direction on the surface in the surface roughness and the interface roughness. Therefore, the investigation about many samples will be necessary in future so that we can use these parameters for the calculation of the x-rays reflectivity in the structure analysis of the similar surface layer and enable structure analysis of good precision.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML