-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Nanoscience and Nanotechnology
p-ISSN: 2163-257X e-ISSN: 2163-2588
2016; 6(1A): 122-131
doi:10.5923/c.nn.201601.24

Numerical Simulation into the Convective Heat Transfer of Al2O3 and Cuo Nanofluids Flowing through a Straight Tube Using the Two Phase Modeling
M. Marzougui , M. Hammami , R. Ben Maad
Laboratory of Energetic and the Thermal and Mass Transfer (LETTM), Faculty of Sciences of Tunis, University Tunis El-Manar, Tunisia
Correspondence to: M. Marzougui , Laboratory of Energetic and the Thermal and Mass Transfer (LETTM), Faculty of Sciences of Tunis, University Tunis El-Manar, Tunisia.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The main purpose of this study is focused on numerical investigation of thermal behavior of Copper oxide-water nanofluids and Aluminum oxide-water nanofluids inside a horizontal heated tube. The model has been solved by using the two-phase models with four correlations of thermal conductivity. The discretization of equations of continuity, momentum, and energy has been done using the Finite Volume Method. A uniform and constant heat flux has been applied at the wall boundary conditions. The results show that the heat transfer coefficient predicted by the two phase model is enhanced by increasing the volume fraction of nanoparticles for all Peclet numbers; when the Peclet number is low, increasing the volume fraction of nanoparticles will enhance the convective heat transfer in the entrances region of the pipe and gradually decrease along the axial distance of the channel. Also, it is found that the enhanced heat transfer is greater for use the models of thermal conductivity which depend on the temperature than in the constant models. Comparison between predicted results and experimental data from literature is carried out which indicates the two phase is more precise.
Keywords: Nanofluids, Heat transfet enhancement, Two phase, Thermal conductivity
Cite this paper: M. Marzougui , M. Hammami , R. Ben Maad , Numerical Simulation into the Convective Heat Transfer of Al2O3 and Cuo Nanofluids Flowing through a Straight Tube Using the Two Phase Modeling, Nanoscience and Nanotechnology, Vol. 6 No. 1A, 2016, pp. 122-131. doi: 10.5923/c.nn.201601.24.
Article Outline
1. Introduction
- In the last decades, the tendency to greater miniaturization of modern equipments and process intensification driven by recent technological development are facing the technological challenge of the efficient cooling of these devices. Indeed, it is required to develop cooling or heat transfer enhancements methods in different process that are able to provide very high heat fluxes [1]. Liquid cooling, also known cooling with liquid, is a very effective way to remove high heat loads from components. However, heat transfer in traditional fluids such as water, ethylene glycol and oil inherently has low thermal conductivity relative to metals and even metal oxides. Therefore, fluids with suspended solid particles are expected to have better heat transfer properties compared to conventional heat transfer working fluids. “Maxwell [2-3]” was the first one who initiated the use of small-sized solid particles inside fluids to increase the thermal properties of fluids by dispersing the particles in the millimeter and micrometers scales. This issue has been carried major problems such as surface abrasion, clogging micro-channels of devices, faster settling time and high pressure drop. Along with the new world of nanotechnology and production of nano-sized particles, a new class of fluids has been introduced as nanofluids to replace conventional thermal working fluid.For first time, “Choi et al. [4]” at American Argonne Institue coined the term nanofluid for fluids with suspended nanoparticles inside. Nanofluids refer to fluids containing nanoscale particles that nanoparticles are usually 1 to 100 nm. Due to the more efficient heat transfer performance than the traditional working fluid, nanofluids present a promising alternative to traditional heat transfer fluids in a wide range of applications in next few years.In the literature, there are many experimental and numerical investigations governing the nanofluid heat transfer and pressure drop. “Anoop et al [5]” had an experimental investigation on the convective heat transfer characteristics in the developing region of tube flow with constant heat flux with alumina–water nanofluids. The results showed that nanofluid with 45 nm particles shows higher heat transfer coefficient than that with 150 nm particles, the enhancement of heat transfer coefficient was around 25% whereas for the 150 nm particle based nanofluids it was found to be around 11%.“Heris et al [6]” did an experimental study on laminar flow forced convection heat transfer of Al2O3 /water nanofluid inside a circular tube with constant wall temperature and reported a significant increase in heat transfer coefficient by increasing the concentration of nanoparticles in nanofluid. They concluded that thermal conductivity increase is not the sole reason for heat transfer enhancement in nanofluids. Other factors such as chaotic movement of nanoparticles, dispersion, Brownian motion and particle migration may play role in heat transfer augmentation due to nanoparticles.From numerical and analytical aspect, the nanofluids studies can be divided to unique single phase and two-phase models. Most of the numerical solutions have been done using a single phase model. “Maiga et al [7]” studied the ethylene glycol- γAl2O3 and water- γAl2O3 nanofluid heat transfer inside a circular minichannel and reported better enhancements of heat transfer for ethylene glycol based nanofluids.“Bajestan et al [8]” carried out another numerical simulation for nanofluid flow through a straight circular pipe in a laminar flow regime and constant heat flux boundary condition and showed that particle volume fraction, Brownian motion and aspect ratio of nanoparticles increase the heat transfer performance.“Kheram [9]” studied the heat transfer and friction factor characteristics of Al2O3 nanofluid in circular tube, he reported that the heat transfer coefficient increases by 8% than that the base fluid and at the same Reynolds number of 700 Nusselt number for 0.4% Al2O3 nanofluids increases by 1.24 times over the base fluid.“Bayat and Nikseresht [10]” considered a single phase containing alumina nanoparticles dispersed in three different base liquids. The numerical results showed that ethylene-glycol based nanofluids shows higher heat transfer performance compared to the water based ones. “Moraveji et al. [11]” investigated the nanofluid flow of water- Al2O3 through a tube under a constant heat flux. The results data showed that the heat transfer coefficient increases by increasing the nanoparticle volume fraction and Reynolds number. Furthermore, the heat transfer coefficient increases by particle diameter reduction.“Ebrahimnia-Bajestan et al [12]” performed a numerical investigation on heat transfer performance and pressure drop of nanofluids. They used a single phase approach to study nanofluids flows through a straight circular pipe in a laminar flow regime and constant heat flux boundary condition. They used Water and ethylene glycol/water as working fluids with particle concentrations ranging between 0 and 6 vol.% for simulating the heat transfer and flow behaviours of nanofluids. They reported that increase of the heat transfer coefficient of nanofluid is caused by the particle volume concentration, Brownian motion and aspect ratio of nanoparticles, while the particle diameter has an opposite effect. Moreover, the heat transfer characteristics of nanofluids are strongly influenced by the type of both base fluid and nanoparticle.“Amir and Seyf [13]” considered a tangential micro heat sink analysis on nanofluid convective flow with alumina nanoparticles dispersed in water. For the results data of the simulations done by them, it was found that using nanofluids as working fluids can cause lower heat transfer entropy generation due to their high thermal properties. With increasing Reynolds number, volume fraction and as well as decreasing particle size the overall entropy generation rate decreases.In contrast to single phase approach, due to the complexity involved in two-phase flow, using the two phase modeling approach for nanofluid has been limited. The two-phase approach seems a better model to describe the nanofluid flow. Some researcher have employed two phase Mixture theory to predict the behavior of nanofluids [14, 15].Based in literature, some important parameters influence on heat transfer enhancements of nanofluids such as diameter of nanoparticles, concentration, temperature, motion, thermal conductivity of working fluid and thermal conductivity of nanoparticles. The aim of this paper is to investigate the heat transfer characteristics numerically for Al2O3/water and CuO/water flow through two-dimensional tube via applying four models (constant and variable models) of thermal conductivity, evaluating its performance and assessment of the results with the proposed correlations. To do this, a two phase numerical method is considered in this study. The required thermophysical properties of the nanofluid were measured and used in the CFD model through UDF (User Defined Function) CFD software ANSYS/FLUENT.
2. Mathematical Modeling
2.1. Thermophysical Properties
- Thermal conductivity is the most high as possible while maintaining a practical, long term heat transfer capability and to test the most appropriate empirical models of thermal conductivity in order to obtain more precise results.In this study, different types of correlations selected from the literature were employed. “Hamilton & Crosser” [16], “Yu & Choi [17]”, “Koo & Kleinstreuer [18]”, and “Corcione [19]” thermal conductivity models. These are used in the current study in the forced convective heat transfer analyses separately.For constant thermophysical properties, the following equations are used for, density and specific heat respectively: [20]
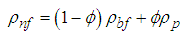 | (1) |
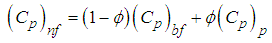 | (2) |
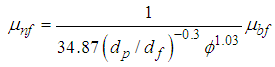 | (3) |
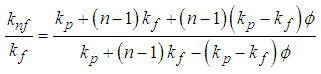 | (4) |
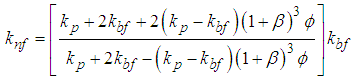 | (5) |
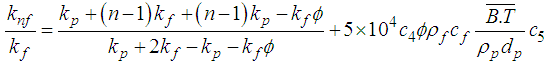 | (6) |
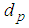 is particle diameter, T is temperature of the fluid, B is the Boltzman constant, and
is particle diameter, T is temperature of the fluid, B is the Boltzman constant, and 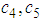 are experimentally determined coefficients that contribute the effects of interaction between particles and temperature, respectively.“Corcione [19]” developed an empirical thermal conductivity correlation. The nanoparticle size, thermal conductivity, volumetric fraction and the base fluid freezing temperature are the key parameters affecting thermal conductivity of the nanofluid. In addition, it is emphasized that the temperature of the nanofluid is important because relative thermal conductivity of nanofluids increases with temperature.
are experimentally determined coefficients that contribute the effects of interaction between particles and temperature, respectively.“Corcione [19]” developed an empirical thermal conductivity correlation. The nanoparticle size, thermal conductivity, volumetric fraction and the base fluid freezing temperature are the key parameters affecting thermal conductivity of the nanofluid. In addition, it is emphasized that the temperature of the nanofluid is important because relative thermal conductivity of nanofluids increases with temperature.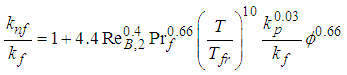 | (7) |
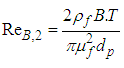 | (8) |
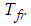 is the freezing temperature of the base fluid and is another definition for the Brownian velocity based Reynolds number.
is the freezing temperature of the base fluid and is another definition for the Brownian velocity based Reynolds number.2.2. Governing Equations
- Mathematical modeling for single- phase (homogeneous) is available in literature, in this model nanofluids can be treated as a pure fluid. Also, the single phase approach is simpler and requires less computational time, which assumes that the phase fluid and ultrafine particles are in thermal equilibrium and move with the same velocity. In this case, all of the classical equations can be adopted for them just using effective thermophysical properties instead of base liquids’ properties.For two phase models, it is assumed that nanofluid was considered as a two phase approach with different temperature and velocity fields. The coupling between phases is strong, and there was a volume fraction of primary phase and also a volume fraction of the secondary phase. Generally, this approach is based on the underlying assumption that each phase can be mathematically described as a continuum, and the governing equations are expressed by the following equations [22]:Continuity:
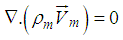 | (9) |
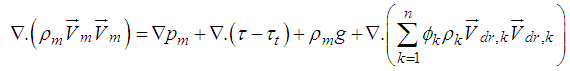 | (10) |
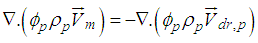 | (11) |
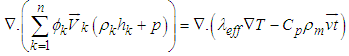 | (12) |
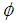 is the volume fraction of phase k, we have:
is the volume fraction of phase k, we have: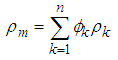 | (13) |
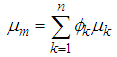 | (14) |
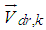 is the drift velocity of secondary phase k, i.e. nanoparticles is the present study and defined as:
is the drift velocity of secondary phase k, i.e. nanoparticles is the present study and defined as: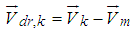 | (15) |
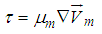 | (16) |
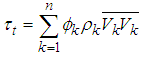 | (17) |
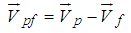 | (18) |
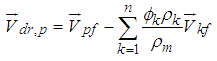 | (19) |
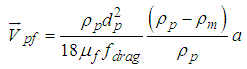 | (20) |
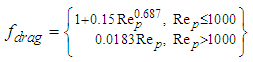 | (21) |
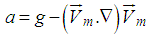 | (22) |
2.3. Topic Geometry and Boundary Condition
- Fig.1 illustrates the geometrical configuration under consideration for our simulation modeling which contains circular copper tube with length (L) of 1.0 m and circular cross section with diameter (D) of 0.007 m. The fluid enters with axial velocity of v0 and uniform temperature of T0 (T0 = 298 K), and considers as steady-state, laminar, incompressible and 2D- Symmetric.
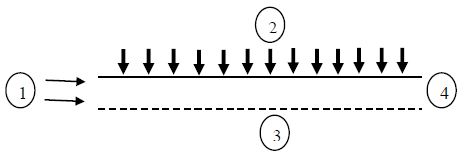 | Figure 1. Flow geometry |
2.4. Numerical Procedure
- To solve the numerical investigation, the CFD module in ANSYS/FLUENT software was employed. This software uses control volume approach to solve this set of nonlinear differential equations. The control volume approach converts the governing equations to set algebraic equations that are solved sequentially throughout the whole domain. The discretization of governing equations was performed using the Volume Finite Method (FVM). A second order upwind Method is used for the convective and diffusive terms. The SIMPLE scheme was adopted as the computational algorithm to couple pressure and velocity and the uniform boundary fitted grid which is finer near the wall because the variables gradient is higher than other positions.
2.5. Validations
- In this study, several grid sizes have been tested to ensure that the variation of number of grid have no affect on the computed results. The selected grids consists of 40
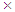 700 cells, in the radial and axial directions, respectively. In order to demonstrate the validity and also the precision of the computed results of the single-phase and the two-phase approaches with constant and variable properties, comparisons with the experimental data given by “Esmaeilzadeh et al. [25]” were made.As shown in Fig. 2a and b, fully developed values of computed heat transfer coefficient are compared with available experimental solutions for water and water- γAl2O3 1% under constant heat flux is about 9000 W/ m2 and Reynolds number equal to 1300. The calculated coefficient of heat transfer shows a significant agreement with experimental results reported in [25]. In addition, the two-phase models considering thermal dispersion and temperature dependent properties are capable to predict the heat transfer behavior more accurately than the single- phase models.
700 cells, in the radial and axial directions, respectively. In order to demonstrate the validity and also the precision of the computed results of the single-phase and the two-phase approaches with constant and variable properties, comparisons with the experimental data given by “Esmaeilzadeh et al. [25]” were made.As shown in Fig. 2a and b, fully developed values of computed heat transfer coefficient are compared with available experimental solutions for water and water- γAl2O3 1% under constant heat flux is about 9000 W/ m2 and Reynolds number equal to 1300. The calculated coefficient of heat transfer shows a significant agreement with experimental results reported in [25]. In addition, the two-phase models considering thermal dispersion and temperature dependent properties are capable to predict the heat transfer behavior more accurately than the single- phase models. | Figure 2. Experimental and predicted heat transfer coefficient for: (a) water and (b) water-γAl2O3 1% as a function axial distance at Re =1300 |
3. Results and Discussions
- The goal of this study is to assess effectiveness of two-phase model considering four models of thermal conductivity for predicting heat transfer enhancement of nanofluids. Therefore, Numerical simulations of two types of nanofluids (water-Al2O3 and water-CuO with
 ) have been done on a wide range of Peclet number for different values of nanoparticles volume fraction. The effects that significantly change heat transfer such as the solid nanoparticles concentration, particle material, Peclet number and thermal conductivity models are stated.
) have been done on a wide range of Peclet number for different values of nanoparticles volume fraction. The effects that significantly change heat transfer such as the solid nanoparticles concentration, particle material, Peclet number and thermal conductivity models are stated.3.1. The Impact of Thermal Conductivity Models on Local Heat Transfer Coefficient
- For a Peclet number of about 5000, the local heat transfer coefficient of the two kinds of nanofluids as a function of the axial distance from the tube inlet at different nanoparticle volume fractions is shown in Fig.3 and Fig.4. At a certain Peclet number and nanoparticle concentration, it is observed that the local heat transfer coefficient of all nanofluids increases with the rise of volume concentration and decreases considerably with an increase in the axial distance from the inlet tube. For the volumetric fraction 1%, the difference among the models and enhancements are relatively low. However, this figure clearly shows large differences among models in heat transfer enhancement for the two nanofluids at 4 vol%. For nanofluids water- Al2O3 Hamilton Crosser gives constant, 8%, enhancement while Yu and Choi gives constant, 13%, enhancement in heat transfer coefficient. Koo Kleinstreuer and Corcione models give the more high values, increasing from 19% to 21%. This is caused by temperature dependency of these models because temperature increases along the channel in heating application of pipes. The reverse of this behavior would be observed, if a cooling application was implemented. This phenomenon, increment of heat transfer enhancement with temperature, is especially important for high nanoparticle volumetric fraction and high temperature variation applications. We can clearly seen that water-CuO nanofluids give higher convective heat transfer coefficients than the water- Al2O3.
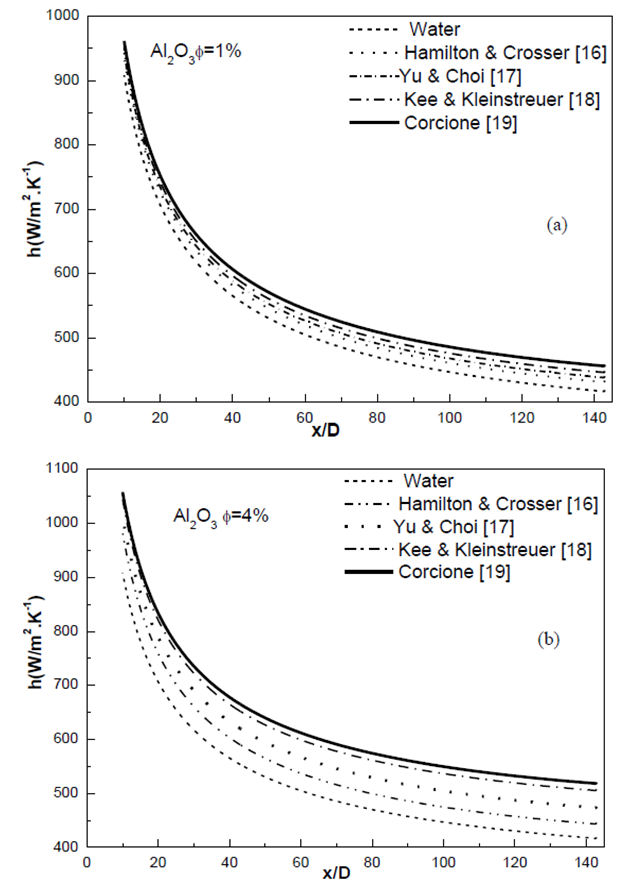 | Figure 3. Local heat transfer coefficient of water -Al2O3 nanofluid at Peclet number 5000 by using the four conductivity models: (a) ɸ=1% and (b) ɸ=4% |
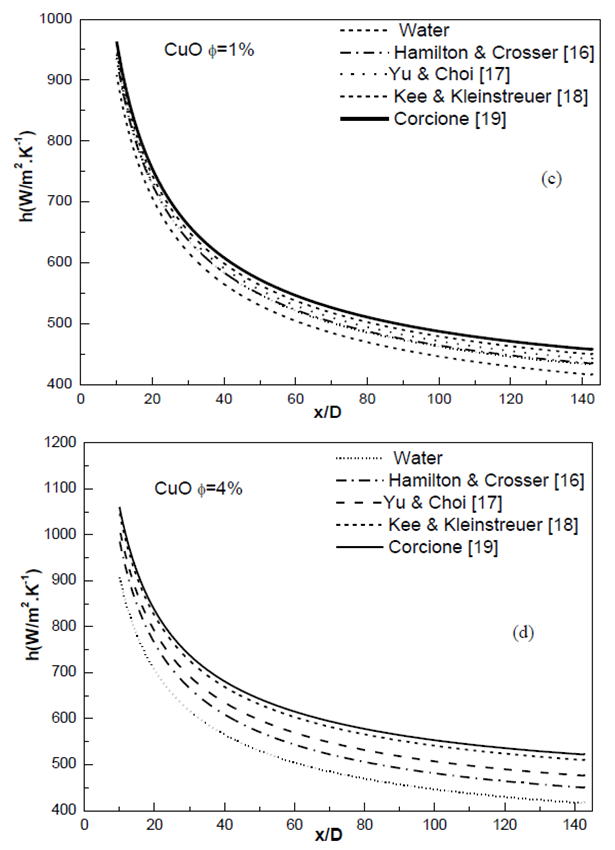 | Figure 4. Local heat transfer coefficient of water -CuO nanofluid at Peclet number 5000 by using the four conductivity models: (c) ɸ=1% and (d) ɸ=4% |
3.2. Peclet Number and Heat Transfer Coefficient
- In this section, the two-phase modeling results are shown in Fig.5 and there are two curves for each volume fraction, which describe the analyses of heat transfer with constant and variable conductivity using the model of Corcione [19] because the analyses with this model are the most reliable ones. As seen, for all the numerical results, the heat transfer coefficient of all nanofluids is highest than of the base liquid and increases linearly with an increase in Peclet number; e.g. when the Peclet number increases from 5000 to 12500, the heat transfer coefficient of Al2O3, CuO nanofluids with a volume concentration of 1% enhances by approximately 32 and 37%, respectively.
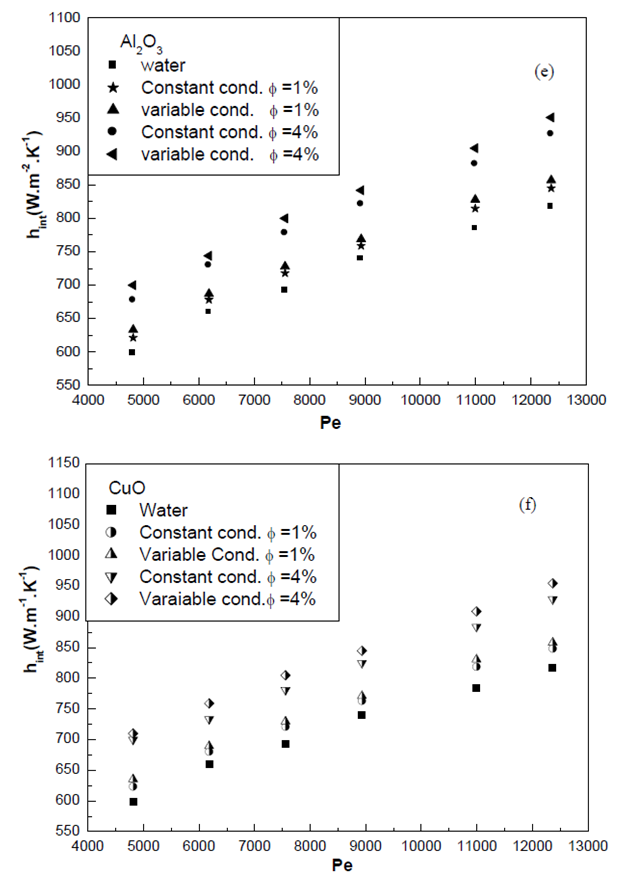 | Figure 5. Average heat transfer coefficient of the all nanofluids as a function of the Peclet number using the model of Corcione [19] |
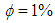 , as shown in Fig. 5e and 5f. It is also noted that with higher thermal conductivity of the mixture, the convective heat transfer between wall and fluid should consequently be more efficient.For example, at Peclet number of about 11000 the deviation from the computed results of average heat transfer coefficients of water- Al2O3 and water-CuO 4% with variable and constant properties is 3 and 2%, respectively.
, as shown in Fig. 5e and 5f. It is also noted that with higher thermal conductivity of the mixture, the convective heat transfer between wall and fluid should consequently be more efficient.For example, at Peclet number of about 11000 the deviation from the computed results of average heat transfer coefficients of water- Al2O3 and water-CuO 4% with variable and constant properties is 3 and 2%, respectively.3.3. Comparison between the Single Phase and Two Phase Models
- Fig.6 illustrates the enhancement of heat transfer coefficient of nanofluids with 4% by volume to that water at Peclet number 12400 for the two approaches. It is clear to see that the two-phase models provide more accurate prediction of heat transfer of nanofluids than the single phase. Similar trends in improvement were observed for other Peclet number. The two phase models are computationally more expensive than single-phase models due to the increased number of equations to be solved.
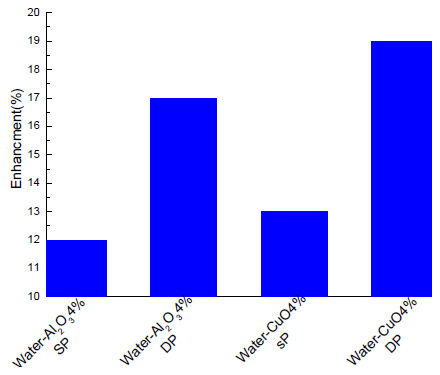 | Figure 6. The percentage of heat transfer enhancement for different types of nanofluids at 4vol% using single-phase (SP) and two-phase (DP) models |
3.4. Thermal Resistance
- In order to evaluate the heat transfer of nanofluids, the thermal performance is evaluated by the total thermal resistance which can be observed in Fig.7.Figure 7 shows the variation of total thermal resistance of the circular tube with volume fraction of different nanoparticles in base fluid. The contribution of the thermal resistance of the nanofluids decreases with increasing volume fraction. The effect of viscosity on the thermal resistance will dominate that of thermal conductivity with further increases in the volume fraction. The results also indicate that the thermal resistance depends on the type of nanofluid. The heat pipe has the lowest thermal resistance using water-base nanofluids containing CuO compared with that of Al2O3. The above points suggest that improvements in the thermal resistance are sensitive to the type of nanofluid and its particle volume fraction.
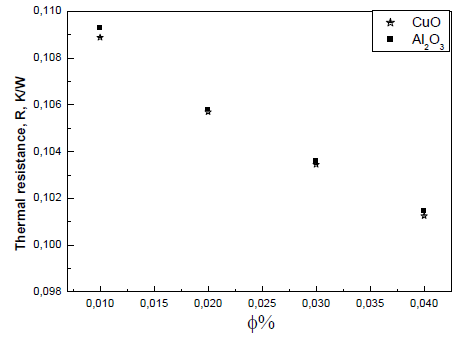 | Figure 7. Variation of thermal resistance with volume fraction of nanoparticles |
4. Conclusions
- In this paper, the Computational Fluid Dynamics models have been used to predict the convective heat transfer coefficient of water-base nanofluids containing Al2O3 and CuO inside circular tube with volume fraction ranging from 1% to 4% using four thermal conductivity models from the literature. The two-phase models have been used in this simulation. It was stated that traditional thermal conductivity correlations and analytical solutions are not capable of accurate estimation of heat transfer coefficient of nanofluids. This may be caused by thermal conductivity variation in nanofluid flow and any other mechanisms which are not considered in traditional models. And, by considering variable thermal conductivity (effect including Brownian motion), we can obtain reasonable results and more heat transfer enhancement of nanofluids. The model of Corcione is chosen the most suitable models for generalized nanofluid heat transfer cases. In other hand, the results showed that the enhancement of the heat transfer rate can be effected by some important parameters such as Peclet number, axial distance, particle volume fraction and the type of nanoparticle material. The thermal resistance is shown to be sensitive to the type of nanofluid and its particle volume fraction. A good agreement between the results obtained from the experimental data from literature and the simulation was observed in the smaller Pe numbers with the two- phase models with variable conductivity.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML