Maya Lakhdara , Saϊda Latreche
Laboratory Hyper frequencies & Semiconductors, Department of Electronics, University Frères Mentouri Constantine, Constantine, Algeria
Correspondence to: Maya Lakhdara , Laboratory Hyper frequencies & Semiconductors, Department of Electronics, University Frères Mentouri Constantine, Constantine, Algeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we present a numerical modelling of a SiGe heterojunction bipolar transistor (HBT) at high temperature, realized in an industrial BiCMOS0.35µm SiGe process, featuring high attractive performances in terms of microwave and low-frequency noise. Electrical modeling is investigated, using, a commercial device simulator SILVACO_TCAD (Silicon Valley Corporation) using macroscopic model Drift–Diffusion Model (DDM) coupled with the thermodynamics model. This method solves the continuity equations for electrons and holes and is coupled with the Poisson equation using a Scharfetter–Gummel approach.
Keywords:
SiGe HBT (Heterojunction Bipolar Transistor), High Temperature, Self-Heating, Numerical modeling, DDM Model, BiCMOS
Cite this paper: Maya Lakhdara , Saϊda Latreche , Modeling and Numerical Simulation of a very High Speed SiGe HBT at High Temperature, Nanoscience and Nanotechnology, Vol. 6 No. 1A, 2016, pp. 92-96. doi: 10.5923/c.nn.201601.18.
1. Introduction
The communication systems have become an important issue for our daily activities. This development would never have been possible without the constant development in new technological fields. To best meet the requirements of communication systems, much of these sectors have been oriented towards the improvement of operating frequencies and lower noise levels of semiconductor components and electronic circuits [1]. At present, the components heterojunction remain the best positioned candidate to fulfill this request operating frequency and low noise level, among these components, the heterojunction bipolar transistor Si/SiGe/Si. The development of bipolar transistors technologies heterojunction Si/SiGe displayed high potential in terms of cutoff frequency offers real possibilities of realization of very fast electronic circuitry [2].In addition, thermal instability is a phenomenon particular to bipolar transistors. Working at high power densities, results in heat generation, which limits the performance of the transistor [3].Any semiconductor component is subject to self-heating when subjected to electrical stress. Indeed, the increase in temperature reduces the carrier mobility and change the bandgap of making semiconductors and thermally dependent on the output current of the transistor.The use of HBT SiGe components in microwave applications that may be exposed to elevated temperatures and operating to high current densities of the component degrades electrical performance and may even cause destruction of the device. The consideration of the temperature and in particular of the self-heating effect in Si/SiGe HBT heterojunction bipolar transistors is a fundamental aspect to predict in a precise way these electric characteristics [4], [5]. The overall goal of this paper is to study the static(IC, IB, β) and dynamics performance of SiGe HBTs 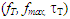 at high temperatures (300 to 450 K), and considering the response at different temperatures. The electrical modeling is investigated, using, a commercial device simulator SILVACO_TCAD (Silicon Valley Corporation) using macroscopic model Drift–Diffusion Model (DDM) coupled with the thermodynamics model. This method solves the continuity equations for electrons and holes and is coupled with the Poisson equation using a Scharfetter–Gummel approach. All important physical effects, such as band gap narrowing, generation-recombination, and mobility dependent for the temperature, are properly modeled and accounted in the numerical simulation of the HBT SiGe device [6].
at high temperatures (300 to 450 K), and considering the response at different temperatures. The electrical modeling is investigated, using, a commercial device simulator SILVACO_TCAD (Silicon Valley Corporation) using macroscopic model Drift–Diffusion Model (DDM) coupled with the thermodynamics model. This method solves the continuity equations for electrons and holes and is coupled with the Poisson equation using a Scharfetter–Gummel approach. All important physical effects, such as band gap narrowing, generation-recombination, and mobility dependent for the temperature, are properly modeled and accounted in the numerical simulation of the HBT SiGe device [6].
2. SiGe HBT Device Structure and DDM Model
The studied structure is a SiGe bipolar transistor integrated using a polysilicon emitter quasi self-aligned structure with selective epitaxial growth of the base, similar to the SiGe HBT investigated in ST-BiCMOS9 0.13-µm technology (figure 1).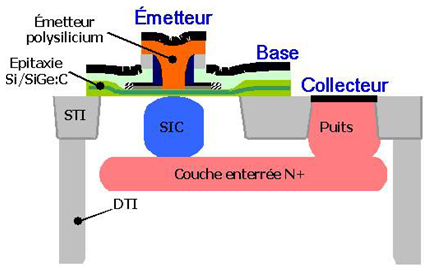 | Figure 1. Schematic cross section of the investigated SiGe Heterojunction Bipolar Transistor [7] |
This structure has a polysilicon emitter with a maximum doping concentration of 1.5 × 1020 cm-3 at the poly/ mono-silicon interface. The collector epilayer thickness is chosen to be 600 nm with doping level peaks at approximately 3. 1016 cm−3. The active base of the transistor is formed by low-energy implantation of the bore, leading to a maximum doping concentration of 2.5 × 1018 cm−3 (figure 2). The SiGe base layer with a thickness of 30 nm is integrated using selective epitaxial growth. The germanium concentration is graded, with Ge = 15-30%.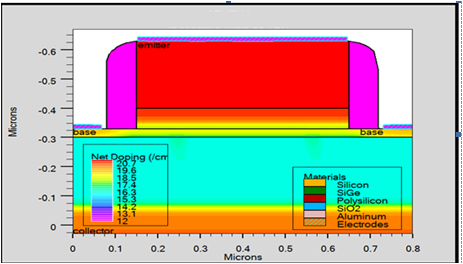 | Figure 2. Concentration of doping in the various regions |
We present the development of the fundamental equations for analyzing the electrical behavior of semiconductors. Our analysis is based on a macroscopic description of semiconductors with possible non-uniform compositions. Various semiconductors differ in their fundamental properties, such as band gap energy, carrier mobility, and effective masses of electrons and holes. In addition, the interfaces between different materials must be properly described.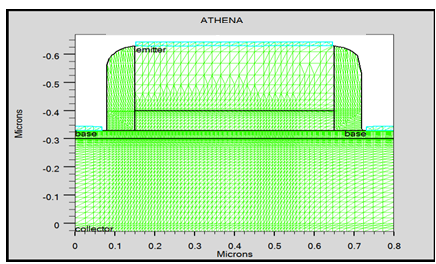 | Figure 3. Mesh structure for a SiGe HBT |
The numerical methods considered here were first applied to hetero-structures through the analysis of solar cells. The model used here is called the DDM (Drift Diffusion Model). The DDM links the ambipolar continuity equation for electrons and holes with the Poisson equation [8].Poisson equation: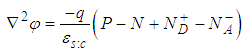 | (1) |
Continuity equations for electrons and holes: 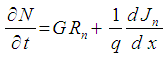 | (2) |
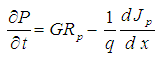 | (3) |
Current equations for electrons and holes: 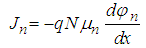 | (4) |
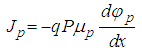 | (5) |
In the Poisson equation, N+D and N-A are the ionized impurity concentrations of donors and acceptors, respectively, ε is the permittivity of the material, and q is the magnitude of the charge associated with an electron or hole. The electron and hole current densities are functions of the concentrations, carrier motilities 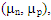 and the quasi Fermi potentials of the electrons and holes,
and the quasi Fermi potentials of the electrons and holes, 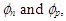 respectively.
respectively.
3. Electrical Characteristics
3.1. Static Characteristics
This paper investigates the temperature dependence from (300 to 450 K) of the DC and AC response of NPN SiGe heterojunction bipolar transistors. First, we describe the principal static characteristics (DC) of a SiGe HBT, particularly the characteristics of the Gummel plots and the current gain. Figure 4 presents the collector current for various temperatures (300 K to 450 K). The collector current increases with an augmentation of temperature. This increase in the collector current can be attributed to diminution of the mobility at the high temperatures. 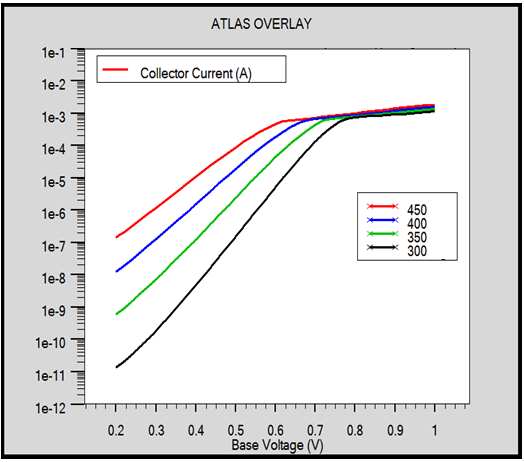 | Figure 4. Collector current as a function (VBE) for high temperature T = 300K, T = 350K, T = 400K, 450K of temperature |
The figure 5 shows the evolution of motilities in an SiGe HBT as a function of the temperature T = 300K, 350K, 400K, and 450K. We note that the carrier mobility decreases with increasing temperature.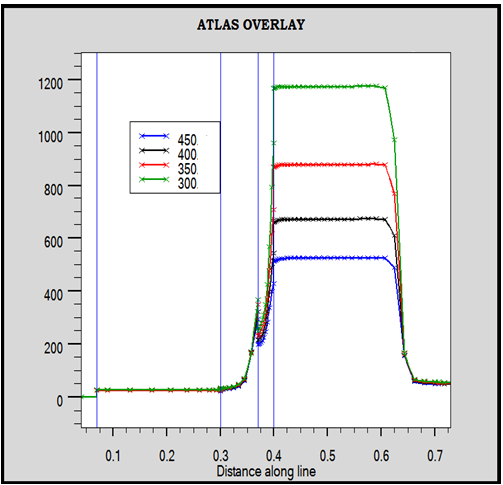 | Figure 5. Evolution of the mobility for SiGe HBT for = 300K, T = 350K, T = 400K, 450K |
Figure 6 represents the variation in the base current in the temperature range from room temperature (300 K) to (450 K). We observe a augmentation in the base current with an increase in the temperature; in addition, The base currents has an coefficient of idealities η is equal to 1.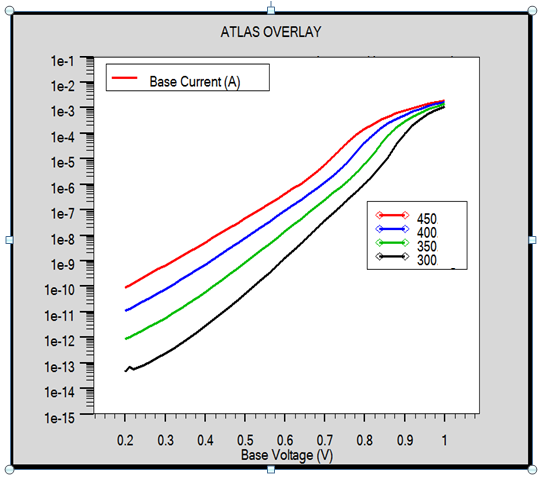 | Figure 6. Base current as a function (VBE) for high temperature T = 300K, T = 350K, T = 400K, 450K of temperature |
The increase of the temperature (300K to 450K) deteriorates the static gain of the transistor (β), this is caused by the increase in collector current (IC) and base current (IB), for high temperatures (over 300 K) the maximum current gain is decreased and shifted towards lower voltages (figure 7).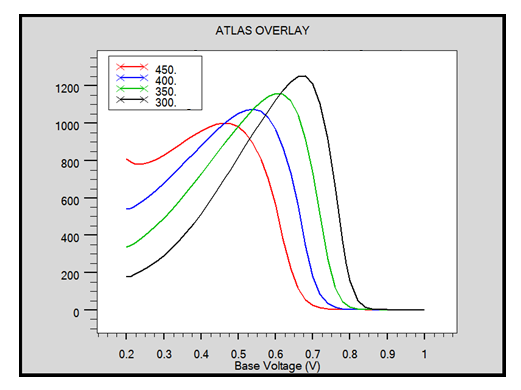 | Figure 7. Evolution of current Gain β(VBE) for SiGe HBT for = 300K, T = 350K, T = 400K , 450K |
The figure 8 shows the collector current IC (Vce) for different base currents and fixed for two temperatures: 300K and 400 K. We can note that the IC characteristics decrease when the temperature increased. 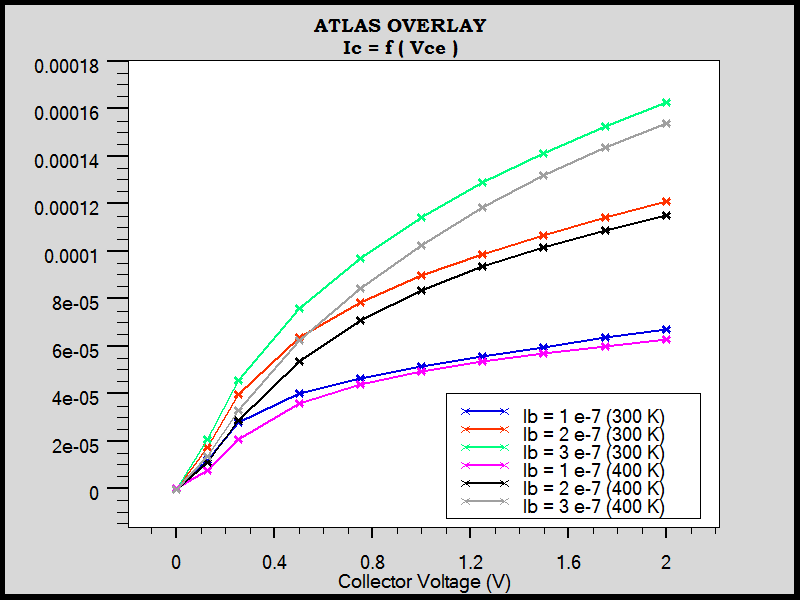 | Figure 8. Characteristics for different values of constants IB, 300K and 400K |
However, as the maximum collector current density decreases at high temperature, the self heating comportment of the SiGe HBT becomes very important.
3.2. Dynamics Characteristics
In most RF and microwave circuit applications, it is the transition frequency response fT that limits system performance. fT depends essentially on transconductance, intrinsic depletion capacitances and carrier transit times. The unity power-gain frequency or maximum oscillation frequency (fmax) is a more relevant figure of merit for practical and microwave applications, since it depends not only on the intrinsic transistor performance, as fT , but also on parasitic of the device, e.g. the total AC base resistance. These two fundamental cut-off frequencies, fT and f max, can be extracted from current and Mason gains, respectively, and h21 and GMU (at 0 dB), themselves, directly calculated from S-parameter-dependent formulae [9].On the other hand, we simulated the dynamic characteristics, the transition frequency fT and maximum oscillation frequency fmax to optimize the microwave performance of HBT.It is interesting to study the evolution of the current gain as a function of the frequency. This current gain in (dB) magnitude will determine the transition frequency fT of the device. For this reason, we set the intersection point at which the modulus of the current gain is equal to 1 at (0 dB) as the transition frequency.The transition frequency fT decreases for high temperatures, we observe that for T = 450 K, the minimum value (fT) is approximately fT = 86 GHz Figure 9.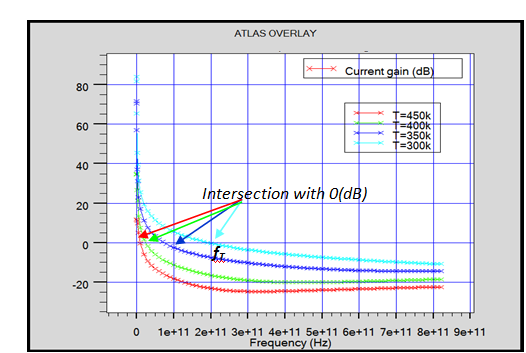 | Figure 9. Current Gain in (dB) as a function of the frequency T=300 K, 350K, 400K, and 450K |
To use a HBT as an amplifier at high frequencies, it is important to study the evolution of the power gain MUG (Mason Unilateral Gain) as a function of the frequency because this determines the maximum frequency of oscillation fmax. The maximum oscillation frequency is the frequency where the Unilateral Power Gain is equal to 1.In the figure 10 the maximum oscillation frequency fmax also decreases at high temperature, fmax decreases from 324GHz for T = 300 to 132 GHz for T = 450K.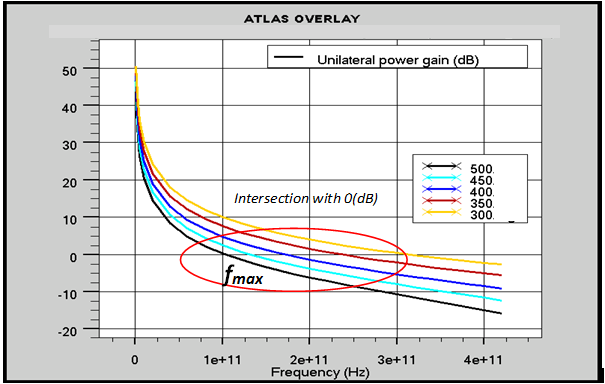 | Figure 10. Unilateral power gain(dB) as a function of the of the frequency T=300 K, 350K, 400K, 450 and 500K |
4. Conclusions
The electrical performances of high-speed SiGe HBTs based on a BiCMOS0.13-µm process were determined at high temperatures. We can conclude that the static and dynamic performances of the HBT are degraded in high temperature. This work allows validating the macroscopic model and thus provides a thermal tool for characterization of the TBH SiGe.We observed an increase in the base current and the collector current with an augmentation in the temperature. Similarly, the current gain (β) decreases at high temperatures; this improvement is appropriate for decreases the carrier mobility and band gap with increasing temperature.We also studied self-heating effect in Si/SiGe HBT at high temperatures on the dynamic characteristics of HBTs. The augmentation of the temperature to 450 K enabled decreases in the transition frequency fT and the maximum oscillation frequency fmax.
References
| [1] | B. Heinemann, R. Barth, D. Bolze, J. Drews, G. G. Fischer, A. Fox, O. Fursenko, T. Grabolla, U. Haak, D. Knoll, R. Kurps, M. Lisker, S. Marschmeyer, H. Rücker, D. Schmidt, J. Schmidt, M. A. Schubert, B. Tillack, C. Wipf, D. Wolansky, and Y. Yamamoto, “SiGe HBT technology with fT /fmax of 300 GHz/500 GHz and 2.0 ps CML gate delay,” in IEDM Tech. Dig., pp. 688–691, 2010. |
| [2] | Michael Schröter, Julia Krause, Niccolò Rinaldi, Gerald Wedel,Bernd Heinemann, Pascal Chevalier, and Alain Chantre, “Physical and Electrical Performance Limits of High-Speed SiGeC HBTs—Part II: Lateral Scaling”, IEEE Transaction on Electron Devices, Vol. 58, N°. 11, November 2012. |
| [3] | J. A. Higgins, « Thermal properties of power HBT’s », IEEE Trans. On Electron Devices, Vol. 40, pp. 2171-2177, 1993. |
| [4] | Z. Huszka, D. Céli, and E. Seebacher, “A Novel Low-Bias Charge Concept for HBT/BJT Models Including Heterobandgap and Temperature Effects—Part I: Theory,”, IEEE Transaction on Electron Devices, Vol. 58, N°. 2, Februry 2011. |
| [5] | A. E. Rafei, A. Saleh, R. Sommet, J. M. Nébus, and R. Quéré, , “Experimental Characterization and Modeling of the Thermal Behavior of SiGe HBTs”, IEEE Transaction On Electrons Devices, Vol. 59, N°. 7, July 2012. |
| [6] | M. Lakhdara, S. Latreche, C. Gontrand, “Mathematical approach and optimisation of nanometric base thickness for a SiGeC HBT dedicated to radiofrequency applications”, Journal of Computational and Applied Mathematics 259 pp. 925–936, 2014. |
| [7] | P. Chevalier, C. Fellous, B. Martinet, F. Leverd, F. Saguin, D. Dutartre et A. Chantre, “180 GHz f T and fMAX self-aligned SiGeC HBT using selective epitaxial growth of the base”, European Solid-State Device Research Conference, pp. 299–302, 2003. |
| [8] | J. C. N. Perez, M. Lakhdara, M. Bouhouche, J. Verdier, S. Latreche, and C. Gontrand “First- and second-order electrical modeling and experiment on very high speed SiGeC heterojunction bipolar transistors”, Semiconductor science and Technology, 24 045010, (2009). |
| [9] | A. de Souza, J.-C. Nallatamby, M. Prigent, and R. Quere, “Dynamic impact of self-heating on input impedance of bipolar transistors,” Electron. Lett., vol. 42, no. 13, pp. 777–778, Jun. 2006. |



 at high temperatures (300 to 450 K), and considering the response at different temperatures. The electrical modeling is investigated, using, a commercial device simulator SILVACO_TCAD (Silicon Valley Corporation) using macroscopic model Drift–Diffusion Model (DDM) coupled with the thermodynamics model. This method solves the continuity equations for electrons and holes and is coupled with the Poisson equation using a Scharfetter–Gummel approach. All important physical effects, such as band gap narrowing, generation-recombination, and mobility dependent for the temperature, are properly modeled and accounted in the numerical simulation of the HBT SiGe device [6].
at high temperatures (300 to 450 K), and considering the response at different temperatures. The electrical modeling is investigated, using, a commercial device simulator SILVACO_TCAD (Silicon Valley Corporation) using macroscopic model Drift–Diffusion Model (DDM) coupled with the thermodynamics model. This method solves the continuity equations for electrons and holes and is coupled with the Poisson equation using a Scharfetter–Gummel approach. All important physical effects, such as band gap narrowing, generation-recombination, and mobility dependent for the temperature, are properly modeled and accounted in the numerical simulation of the HBT SiGe device [6]. 


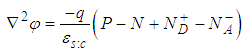
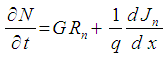
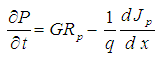
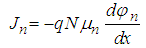
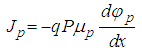
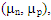 and the quasi Fermi potentials of the electrons and holes,
and the quasi Fermi potentials of the electrons and holes, 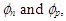 respectively.
respectively. 






 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML