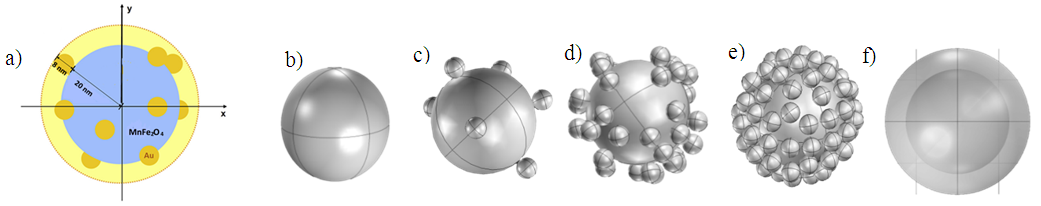Samir Taloub 1, Farida Hobar 1, Iordana Astefanoaei 2, Ioan Dumitru 2, Ovidiu Florin Caltun 2
1Laboratory of Microsystems and Instrumentations (LMI), Electronic Department, Faculty of Science Technology, Constantine 1 University, Constantine, Algeria
2Laboratory of Magnetic Materials for Technological Applications (LMAT), Faculty of Physics, AlexandruIoanCuza University, Iasi, Romania
Correspondence to: Samir Taloub , Laboratory of Microsystems and Instrumentations (LMI), Electronic Department, Faculty of Science Technology, Constantine 1 University, Constantine, Algeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Magnetic nanoparticles (MNPs) are of particular interest for biomedical application such as single molecule detection, drug release or magnetic hyperthermia treatment. The concept of hyperthermia is to use MNPs to heat a region of the body affected by cancer to temperatures between 42°C to 48°C. At these temperatures, the cancerous cells can be destroyed. In this paper, it was modeled the heating process of a single MNP inserted in a biological tissue under an external appliedmagnetic field. Using the finite element analysis in COMSOL Multiphysics software, it was analyzed the thermal response of MNPs with different shapes: sphere, cube, rod and core-shell structure materials and/or thickness. The results demonstrate the impact of nanoparticle shape and surface coating in temperature dissipation in and around the nanoparticle.
Keywords:
Magnetic nanoparticles, Surface coating, Hyperthermia, Core-shell structure, COMSOL Multiphysics
Cite this paper: Samir Taloub , Farida Hobar , Iordana Astefanoaei , Ioan Dumitru , Ovidiu Florin Caltun , FEM Investigation of Coated Magnetic Nanoparticles for Hyperthermia, Nanoscience and Nanotechnology, Vol. 6 No. 1A, 2016, pp. 55-61. doi: 10.5923/c.nn.201601.10.
1. Introduction
Magnetic hyperthermia is a novel method of cancer treatment. In the domain of oncology therapeutics, hyperthermia is a general term used for describing the increasing of the temperature of tissue above the normal physiologic level within targeted cancerous cells without damaging the surrounding healthy tissue [1-4]. Magnetic nanoparticles have been recognized for potential use in hyperthermia, and the treatment consists in the introduction of ferromagnetic or super-paramagnetic particles into the tumor tissue [5]. Depending on the size of MNP these can be found in the following magnetic states [6]: superparamagnetic, single-domain or multi-domains ferro or ferromagnetic. The alternating magnetic field produces the heating of MNP by three major mechanisms [6]: hysteresis loss, Neel and Brownian relaxation. The heating of multi-domain MNP in AC magnetic field occurs mainly due the hysteresis loss (magnetization lags in time behind the applied magnetic field). Superparamagnetic MNP with small size (less than 20 nm for Fe3O4) are the single-domain MNP that have not hysteretic behavior, so the power generates by relaxation process. Eddy current heating is assumed negligible due to the small size of the particles [7]. The heatingprocess depends on particle size, shape and nature, but also onthermal characteristic of tissue as well on magnitude and frequency of the applied magnetic field.In the design of MNPs, with the selection of a suitable magnetic core, fine tuning of surface coating materials for functionalization and biocompatibilization represents a major challenge for the practical use of MNPs in clinical applications. The coating can consist of long-chain organic ligands or inorganic/organic polymers, noble metals (gold, silver), etc. This surface coating is important for i) prohibiting agglomeration (clustering) of MNPs due to the interparticle interactions and eventually providing the colloidal stability of water/organic solvent based suspensions / solutions (ferrofluids) prepared with MNPs ii) providing biocompatibility of MNPs by preventing any toxic ion leakage from magnetic core into the biological environment iii) serving as a base for further anchoring of functional groups such as biomarkers, antibodies, peptides, etc. [8, 9].The researchers just recently are aware of the distinct properties of amorphous and /or crystalline core-shell structure and the related potential medical applications. The synthesis of gold nanoshells usually involves gradual deposition of small gold colloids onto the surfaces of cores grown by the Stöber method [10]. The gold particles then grow and coalesce, from isolated islands to incomplete irregular coating, finally form a continuous complete shell covering the core. In this paper, we report a comparative study of the heat generation of a single nanoparticle (MnFe2O4) with various shapes (sphere, cube and rod) and the same volume (Vsphere=Vcube=Vrod) encased in a spherical cell or tissue region. The proposed model describes the spatial-temporal temperature distribution and the thermal effects due to heat propagation in the tumor cell during the treatment. After that, we study effect of different coating materials; as polymer and gold, the shell thickness of the chosen materials play an essential role on the temperature response of the system (augmentation/diminution) through the influence of thethermal characteristics of the used materials. It was simulated the incomplete coating surface with different amount of the nanoparticles attached to the surface of the magnetic core with related hyperthermia behavior. Finite element simulations of the heating process of nanoparticles were carried out using COMSOL Multiphysics (heat transfer module). The simulations analyses the temperature profile (heat dissipation) in and around the nanoparticle.
2. Methods
It was considered an individual magnetic particle inside a spherical domain of tissue with the radius of 0.5 µm (Fig.1.). The spatio-temporal temperature distribution given by the MNP was analyzed in COMSOL Multiphysics [11].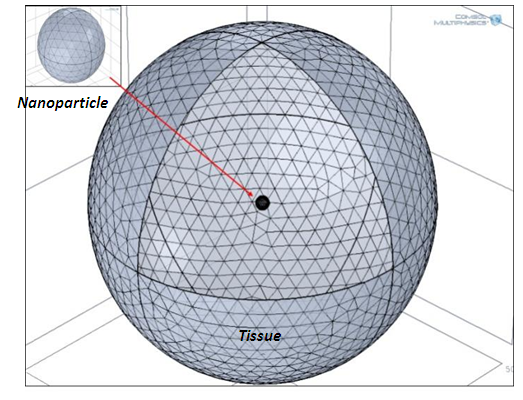 | Figure 1. The geometry discretization |
The main goal was to analyze the thermal response of the living tissue when a nanoparticle used as heating source has i) different shapes (sphere, cube and rod) and ii) complex core-shell structure. The temperature distribution T(x, y, z, and t) in the tumor cell is given by the solution of the Fourier heat transport equation: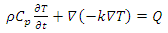 | (1) |
where ρ is cell density, CP is specific heat capacity at constant pressure, k is cell thermal conductivity and Q is the heat dissipated by nanoparticle in the volume of the cell. Volumetric power density was considered constant: Q = 1016(W/m3) as in the reference [12]. At the beginning of the heating process the temperature of the tissue is considered Ti = 37°C, normal temperature of human body. The geometry given by the MNP and tissue was discretized by free tetrahedral elements on all domains (Fig.1.), the complete mesh consists of 62070 domain elements. The boundary conditions are considered the following:1) the thermal flux from the particle is completely received by the tumor cell (the continuity of the thermal flux between domains)2) the temperature on the outer surface of tissue is maintained at body temperature T0 = 37°C.The following shapes: sphere, cube and rod were considered for the MP (Fig. 2). Firstly it was considered a spherical nanoparticle with radius of 20 nm. To obtain the same volume for the particles with different shapes - the dimensions for nanocube and nanorod were computed. i) The particle with nanocube shape has the side length of Lc = 32 nm and ii) the nanorod as a cylinder has the length Lsyl=73 nm and hemispherical caps with radius Rcyl = Rcap=11 nm.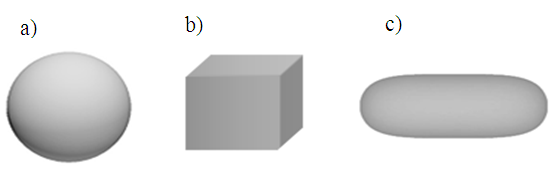 | Figure 2. The different shapes used in simulation: a) Sphere, b) Cube and c) Rod |
In order to further investigate the effect of thickness of coating surface, models of nanoshell with two different materials were studied. Au and PEG polymer shell with thicknesses of: 5, 10, 20, 30 and 40 nm covering the magnetic core of MnFe2O4 and 20 nm in radius was considered in order to determine the thermal evolution of the proposal structure. The irregular coating surface was simulated; a comparison of thermal response of spherical and ellipsoidal surface coating was established, it was chosen a gold spherical shell with 10 nm of thickness, and two ellipsoidal shell (ellipsoid1: 25-25-43.2 nm, ellipsoid2: 22-25-49 nm) the radius of magnetic core was taken 20 nm.On the other hand, it was modeled an incomplete nanoshell in which many gold nanoparticles 4 nm in radius, are attached on to the surface of a magnetic core with the radius of 20 nm as shown the Fig. 3. The heat dissipation of the incomplete shell with possible covering surface without collision between particles are investigated quantitatively.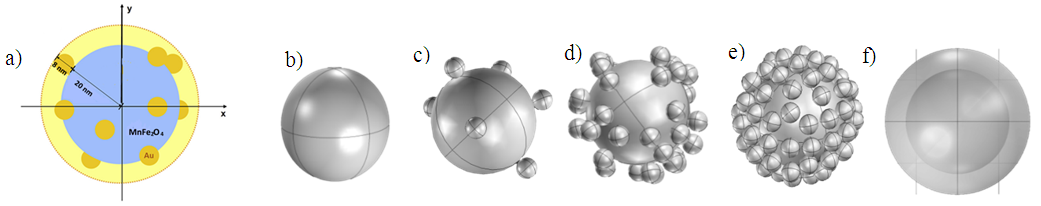 | Figure 3. Incomplete shell structure simulated in COMSOL: (a) the radius of naked magnetic core was chosen to be 20 nm, gold nanoparticles with 4 nm in radius was attached to the surface of the magnetic core (complete shell thickness 8 nm). (b) Magnetic core, (c) (d) (e) 10, 40, 80 gold nanoparticles attached on the surface respectively, f) complete shell |
Magnetite (Fe3O4) and ferrite MnFe2O4 nanoparticles are often selected for biomedical applications due to their chemical/magnetic stability and low cytotoxicity [13]. In all simulations MnFe2O4 was chosen as magnetic particle which is a heat source for cell. MnFe2O4 is good candidates since it offer high magnetization values which is important for hyperthermia applications. Thermal properties of different materials used in simulations are presented in Table 1:Table 1. Thermal properties of the materials used in simulations
 |
| |
|
3. Results and Discussion
3.1. The time evolution of temperature and thermal equilibrium of the tumoral cell determined by the heating of the MNP with different shapes is presented in the Figure 4.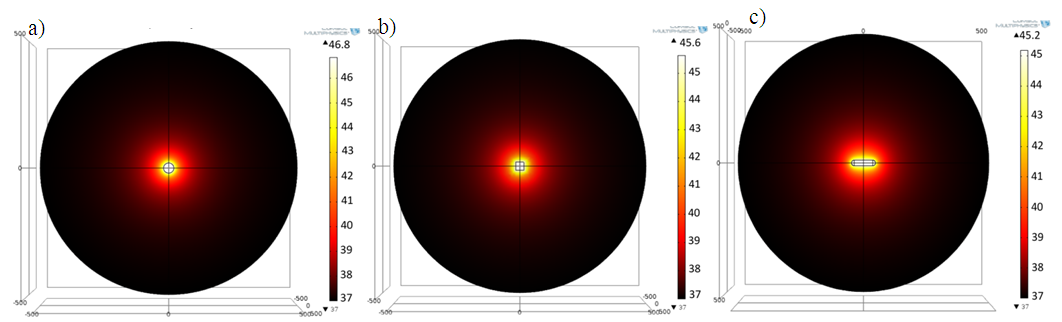 | Figure 4. The 2D spatial temperature distribution on z-y direction for 1μm tumoral cell of a) sphere, b) cube and c) rod, after 3μs from the beginning of heating process |
As shown in the scale of Figure 4.a difference in temperature achieved by the simulated shapes was observed, this difference in temperature can be explained by the difference of the proportional surface of etch shape, taking into account that the thermal response depend on the heat generation by unit of volume (general heat source) and unit of surface (boundary heat source). The maximum values of the temperatures were: for sphere Tmax = 46.8°C, for cube Tmax = 45.6°C and for rod Tmax = 45.2°C. These maximums are achieved in the center of the particles and disperse on the surrounding medium (Fig.5). The distribution of the thermal field in the therapeutic range achieved by rod shape is larger than sphere and cube.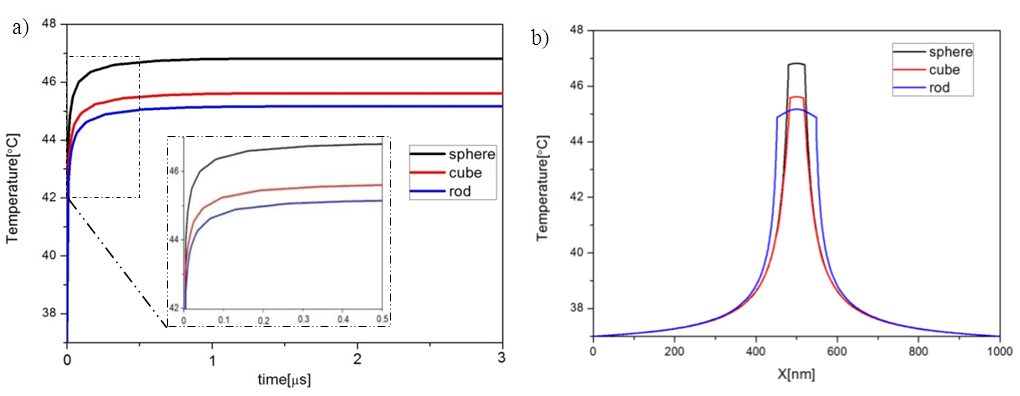 | Figure 5. The spatial and temporal evolution of the temperature for the three different NPs shapes (Sphere, Cube and Rod). (a) Temporal evolution in the point x=0 (center of the heat source); (b) the radial temperature distribution after 3μs from the beginning of heating process |
The success of a hyperthermia cancer treatment requires minimizing the applied power to improve the thermal performance in biomedical applications. Size and shape-dependent for therapeutic effects of MNP in 3.2. The MNPs covered by different materials are used in the hyperthermia applications to provide a functional surface or biocompatilization. On this part of simulations, the influence of the coating surface on temperature dissipation within the surrounding medium was studied. It was modeled a core-shell structure with magnetic core of MnFe2O4 used as heat source and gold or polymer like shell. An opposite aspect of heat dissipation was observed (decreased for gold and increased for polymer) proportional with shell thickness due to on the thermal conductivity coefficient for both simulated shell materials.To study a functional MNP (core-shell structure) and related hyperthermia process, it was selected a spherical shape to get the maximum temperature for designated nanoparticle volume (sphere with 20 nm in radius). In this case, it was simulated the temperature induced by the heating of the MnFe2O4 nanoparticle covered by a shell using two different materials: Au and PEG Polymer. The change in temperature distribution for different thickness of the shells can be observed in figure 6. The temperature decreases with the increase of the shell thickness for gold shell. Also, the temperature increases with the increase of the shell thickness for the polymer shell. Gold shell with a higher value of conductivity transfer more rapidly the heat generated by the magnetic core to the external medium, On the other hand within the polymer coating the heat generated was preserved inside the particle and ensure the temperature rise up to reach thermal equilibrium. The high thermal conductivity coefficient of the gold shell and the small coefficient of polymer influence significantly the temperature within cell. The select of the suitable material and shell thickness to achieve desired temperature for hyperthermia depend on the specific region of application in human body.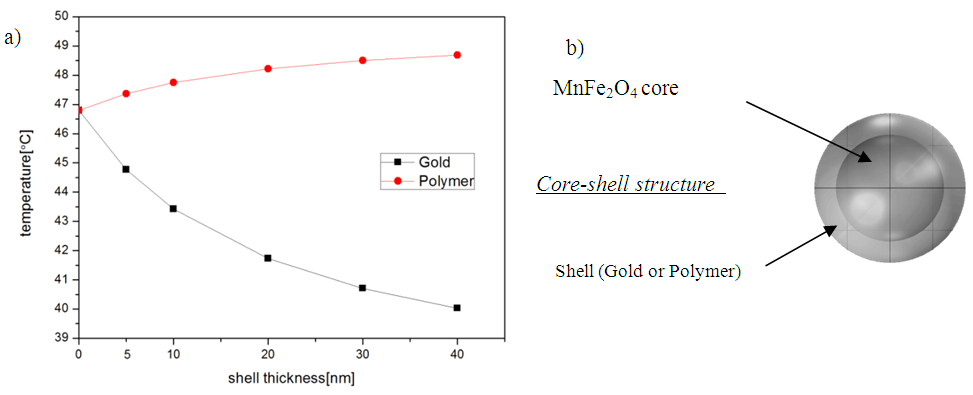 | Figure 6. a) The maximum temperature achieved by following surface coating thickness (5, 10, 20, 30 and 40 nm): gold (black line) and polymer (red line). b) simulated core-shell structure |
In order to investigate the effect of irregular coating surface, it was compared the temperature distribution for two different form of surface coating (Fig.7), spherical shell 30 nm in radius and two ellipsoid (elipsoid1: 25-25-43.2 nm, elipsoid2: 22-25-49 nm) with Vsphere=Velipsoid1=Velipsoid2,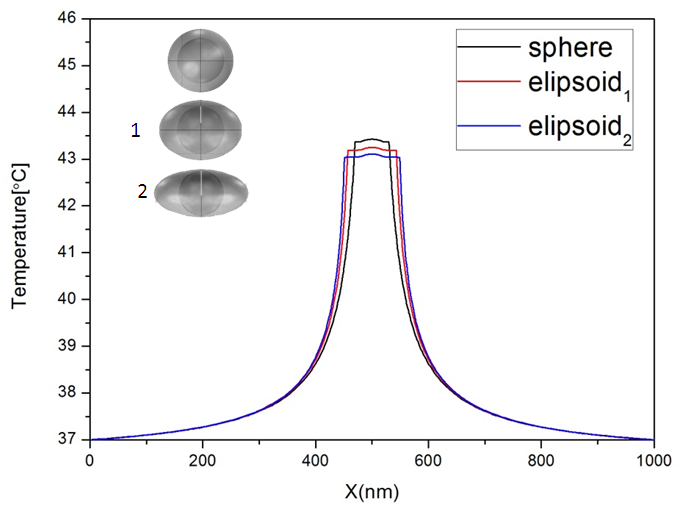 | Figure 7. a) The radial temperature distribution for different form of surface coating, sphere 20 nm in radius, elipsoid1: 25-25-43.2 nm, elipsoid2: 22-25-49 nm. Vsphere = Velipsoid1 = Velipsoid2 |
As shown in Figure 7 for ellipsoid the thermal field is inferior to spherical shell but without big differences in the maximum temperature achieved by the heat sources: 43.4, 43.2 and 43.1°C for sphere, ellipsoid1 and elipsoid2 respectively, the effect of the surface coating anisotropy in hyperthermia is not very important.3.3. The Au-MnFe2O4 NPs combine both magnetically active MnFe2O4 and optically active Au within one nanostructure which is a promising NP platform for multimodality imaging and therapeutics. In this case the understanding of the thermal profile of this structure is indispensable taking into account the surface coating growth within the synthesis process. It was simulated a single nanoshell embedded in spherical tissue 0.5µm in radius, when small gold nanoparticles (4 nm in radius) are attached on to the surface of the magnetic core (20 nm in radius). It was calculated the volume coverage ratio (%) from the volume occupied by gold nanoparticles relative to the volume of a complete shell, to define the temperature profile for the incomplete covered nanoparticle with different amount of the attached nanoparticles. as shown in Figure 7. An evolution of thermal response was observed. The maximum temperature on the nanoparticle surface Tmax=46.8°C was obtained for uncovered MNP, A continuous decrease of the temperature related with the volume/coverage ratio was observed and obtained a minimum value of the temperature Tmin=43.9°C for MNP with a complete shell.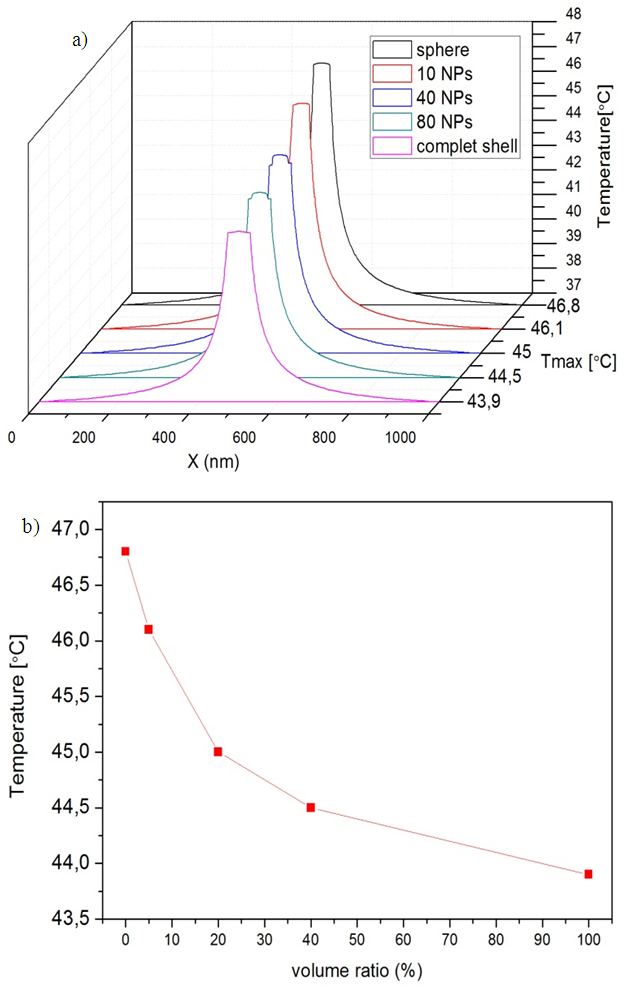 | Figure 8. a) The radial temperature distribution for different amount of surface coating after 3μs from the beginning of heating process. b) The temperature evolution relative with the volume ratio (%) |
4. Conclusions
In our simulations was used a magnetic nanoparticle consisting of only one magnetic domain of MnFe2O4 ferrite since it offer high magnetization values that are important for hyperthermia applications. The study can be extended to different kind of magnetic materials and type of shells. In a simple way we have demonstrated that the temperature achieved by same volume of magnetic materials is maximum for a spherical particle comparing with cubic or rod shaped nanoparticles. Because was used the same volume and specific absorption rate particle the thermal field covers more central volume in the case of rod shape particles while, the thermal equilibrium is reached at the same time of 1µs from the beginning of the heating process for all the three simulated shapes.Thickness and shape uniformity was studied and we note that the temperature profile related on the rapport material/thickness of surface coating, the thermal properties of shell defined the aspect of temperature evolution (increase/decrease). Shell thickness uniformity enables some change in maximum temperature achieved by the magnetic core but still insignificant (less than 0.5°C).The uncompleted surface coating effect was studied, it was simulated the thermal response of different covering volume ratio of gold shell, and was shown that the open surface left through the shell growth process influence significantly on the temperature profile evolution.The use of nanoparticles which are composed of a magnetic core surrounded by a functionalized biocompatible surface shell, depend on the selection of the suitable materials (core-shell), surface coating thickness and surface uniformity.
ACKNOWLEDGMENTS
Samir Taloub acknowledge the financial support of Constantine 1 University for his research stage at AlexandruIoanCuza University of Iasi.Ioan Dumitru acknowledge the support given by Romanian CNCS-UEFISCDI under project PN-II-RU-TE-2012-3-0449.
References
| [1] | M. Brzeska, M. Panhorst, P. B. Kamp, J. Schotter, G. Reiss, A. Pühler, A. Becker, H. Brückl .J. Biotech. 25 (2004) 112. |
| [2] | A. Ito, M. Shinkai, H. Honda, T. Kobayashi, J. Bio. Bioeng. 1 (2005) 100. |
| [3] | R. Heart and S. Dutz. J. Magn.Magn.Materials. 187 (2007) 311. |
| [4] | G.F. Goya, V. Grazu and M.R. Ibarra.Current Nanosci. 1 (2008) 4. |
| [5] | K.L. Ang, S. Venkatraman, and R.V. Ramanujan. J. Materials Science and Engineering C 27 (2007) 347. |
| [6] | S.N. Tabatabaei, J. Lapointe and S. Martel. J. IEEE. IROS. (2009) 546-551. |
| [7] | L. Roizin-Towle, J.P. Pirro.J. Radiat Oncol Biol Phys.20(4) (1991) 751-6. |
| [8] | D. J. L.ormann, R. Cherkaoui, L. Spinu, M. Nogues, F. Lucari, F. Orazio, D. Fiorani, J. Magn. Magn. Materials. 187 (1998) 139-144. |
| [9] | D. Fiorani, J. L Dormann, R. Cherkaoui, E. Tronc, F. Lucari.J. Magn.Magn.Materials. 196-197 (1999) 143-147. |
| [10] | W. Stöber, A. Fink, E. Bohn, J. Colloid Interface Sci. 26 (1968) 62. |
| [11] | COMSOL Multiphysics, Heat Transfer Module, Users’s guide, 2008. |
| [12] | J. Pearce, A. Giustini, R. Stigliano, P. Jack Hoopes . J. Nanotechnology in Engineering and Medicine. 4 (2014) 011007-1. |
| [13] | N. Lewinski, V. Colvin, R. Drezek. Cytotoxicity of nanoparticles. J.Small. 4(1) (2008)26–49. |
| [14] | D.H. Kim, D.E. Nikles, C.S. Brazel. J. Materials. 3 (2010) 4051-4065. |
| [15] | A.O. Govorov, W. Zhang, T. Skeini, H. Richardson, J. Lee, N.A.Kotov.J.NanoscaleResLett.1 (2006)84–90. |




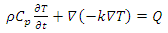




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML