1. Introduction

Photonic crystals (PCs) are defined as periodic structures having a refractive index that is modulated with a wavelength-scale periodicity in one, two or three dimensions. This periodicity results in a wavelength region called the photonic band gap (PBG), in which propagation of electromagnetic radiation is not allowed [1], [2]. By use of PBG we can control the behavior of light inside PCs in very small spaces that is the key for designing ultra-compact devices based on PCs which are suitable for optical integrated circuits.

Power splitters [3], channel drop filters [4], reflectors [5], and demultiplexers [6] are some examples of optical devices designed based on photonic crystals. Channel drop filters (CDFs) that access one channel of a wavelength division multiplexing (WDM) signal while leaving other channels undisturbed are essential components of photonic integrated circuits (PICs) and optical communication systems [7].

In the literature, several topologies have been proposed for designing photonic crystal CDFs: by utilizing the resonant coupling between micro-cavity modes produced by point defects and waveguide modes created by line defects [8], [9], or by the non resonant coupling between two parallel photonic crystal waveguides placed in proximity [10], [11]. Photonic crystal ring resonator (PCRR) is another popular device used for designing channel drop filters. The concept of PCRR was introduced for the first time by Kim et al. [12], where they proposed and demonstrated a two-dimensional photonic crystal (2D-PC) laser based on the hexagonal waveguide ring resonator. Later in the literature, several works based on PCRRs were presented for realizing switches [13], power splitters [14], and demultiplexers [15]. Compared to point-defect cavities, ring resonators offer scalability in size, adaptability in structure design because of vast design parameters and flexibility in mode design due to their multi-mode nature. Recently, several types of CDF based on 2D-PCRR have been proposed using square PCRR [16], hexagonal PCRR [17], circular PCRR [18], X-shaped PCRR [19], and elliptical PCRR [20].

In this study, we demonstrate a new design of T-shaped channel drop filter based on square photonic crystal ring resonator with circular inner rods configuration by using the finite difference time domain (FDTD) method. The structure consists of two photonic crystal waveguides and a single photonic crystal ring resonator between them. Afterward, the impact of varying different parameters on the filtering behavior of the proposed structure is investigated. In our design, 100% dropping efficiency with quality factor of 502 is achievable at wavelength λ=1.578487 μm, which is a satisfactory result in comparison with previous T-shaped channel drop filters based on photonic crystal ring resonators.

2. Design of the Channel Drop Filter

The considered photonic crystal structure is formed by a two dimensional square lattice of dielectric cylindrical rods of silicon (Si) embedded in an air background. Rods have a refractive index value of n=3.48, and a radius of r=0.105*a, a=685 nm being the lattice constant of the photonic crystal structure which is defined as the distance between centers of two adjacent rods. According to the band structure, obtained by plane wave expansion (PWE) method, there is a photonic band gap for TM (transverse magnetic) modes in the normalized frequency range of 0.406–0.493 (a/λ), as shown in Figure 1, where λ is the wavelength in free space, which corresponds to the wavelength range of 1.389–1.687 (μm). Light with TM polarization will not be allowed to propagate in the PC within the aforementioned range.

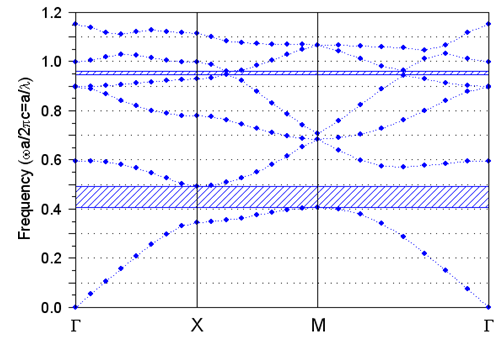Figure 1. Dispersions curves and band gaps for TM polarization for the photonic crystal structure without defects

Figure 2 shows the schematic structure of the proposed T-shaped channel drop filter. This structure is composed of a square photonic crystal ring resonator with circular inner rods configuration and two photonic crystal waveguides. The input waveguide (bus waveguide) is created by removing a complete row of dielectric rods in horizontal direction, whereas the output waveguide (drop waveguide) is created by removing a complete row of dielectric rods in vertical direction. The ring resonator is obtained by removing a ring shape of dielectric rods from the PC structure. The circular configuration of the inner rods is built by varying the position of eight inner rods, indicated with blue color in Figure 2, from their original positions. In order to improve the dropping efficiency, four green rods are placed at the corners of the square ring and one at the upper corner of the drop waveguide. All of these green rods are completely similar to the other rods in the structure. The incident port and exit ports are labeled as A, B, and C, respectively. Because of the coupling between the waveguide and the ring resonator at resonant wavelength, the electromagnetic energy propagating in the horizontal waveguide will be transferred to the vertical waveguide through the resonant ring and traveled toward port C. When the ring does not resonate, the electromagnetic energy remains in the horizontal waveguide and goes through port B.

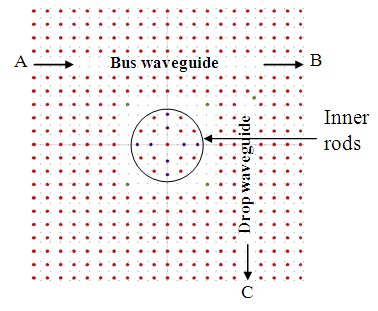Figure 2. Schematic structure of the proposed T-shaped channel drop filter

3. Simulation and Results

After designing the proposed channel drop filter, we simulated the structure and obtained the output spectrum of the filter. For this purpose, we employed the finite difference time domain (FDTD) method [21]. This method is used for obtaining the distribution patterns of optical waves and the transmission properties of PC-based devices. Perfectly matched layers (PML) are located around the whole structure as absorbing boundary conditions. A Gaussian input signal is launched into the input port A. Power monitor was placed at the output ports B and C to collect the transmitted spectral power density after Fourier-transformation.

The CDF response is shown in Figure 3. As shown, 100% coupling and 100% dropping efficiencies can be achieved for the proposed T-shaped channel drop filter. The resonant wavelength of this filter is observed at λ=1.578487 μm. The quality factor (Q) factor can be calculated with Q=λ/Δλ, where λ and Δλ are resonant wavelength and full width at half maximum (FWHM), respectively. The obtained value of Q for this structure is 502. Compared with previous T-shaped channel drop filters based on photonic crystal ring resonators, coupling and dropping efficiencies of our T-shaped channel drop filter are better than of the results reported in References [22-24]. The quality factor of our CDF is much better than the Q obtained in references [22-24]. Another advantage of our proposed channel drop filter is its small footprint 189.66 μm² compared with CDF proposed in reference [23]. Therefore, these characteristics make the proposed structure useful for application in optical communications systems.

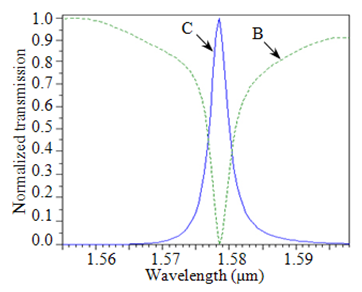Figure 3. Normalized transmission spectrum of the proposed filter

In order to demonstrate the filter performance, we simulate the field distribution of this filter for two different wavelengths. The result is depicted in Figure 4. As shown in the Figure 4, at resonant wavelength, the field of the bus waveguide is fully coupled with the ring and reached into the output port C. In this condition, there is no signal flow in port B. whereas at off-resonance it does not couple and continues to propagate through the bus waveguide.

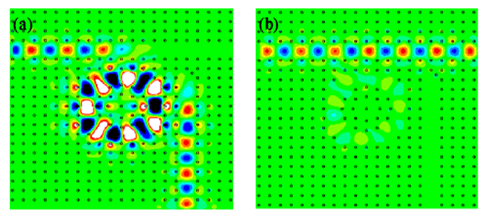Figure 4. Field distribution at a) λ=1.578487 μm (the resonant wavelength), b) λ=1.555 μm (the off-resonance)

4. Parameters Affecting Resonant Wavelength and Dropping Efficiency

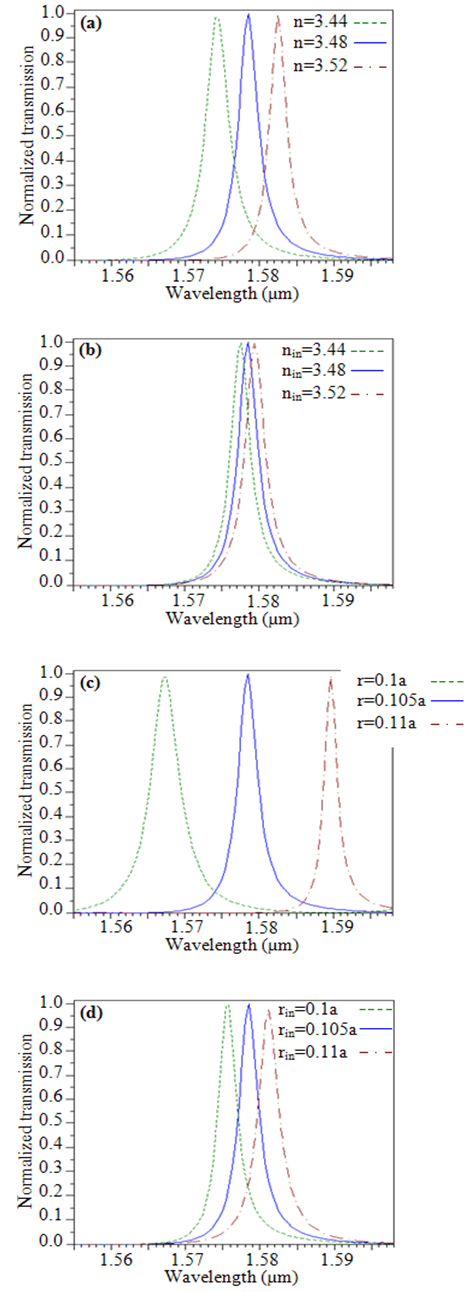
According to the results shown above, we can investigate parameters that affect resonant wavelength and dropping efficiency in photonic crystal CDFs. These parameters include refractive index, radius of inner and whole rods. The first parameter we are going to change is the refractive index of rods. Figure 5a illustrates the normalized transmission spectra at port C for different refractive indices of whole rods, n=3.44, n=3.48, and n=3.52, respectively. As can be seen, by increasing the refractive index of the whole rods, the resonant pick moves to higher wavelengths without significant change in the dropping efficiencies values. The obtained output wavelengths are λ=1.574059 μm, λ=1.578487 μm, and λ=1.582493 μm, respectively. In this structure, the channel spacing is about 4 nm.

Figure 5b shows the normalized transmission spectra at port C for different refractive indices of the inner rods, n_in=3.44, n_in=3.48, and n_in=3.52, respectively. As shown in Figure 5b, by increasing the refractive index of the inner rods, the resonant wavelength shifts toward higher wavelengths. The dropping efficiency is approximately constant for different values of refractive indices of the inner rods. With different refractive indices of the inner rods equal to n_in=3.44, n_in=3.48, and n_in=3.52, we obtained wavelengths of λ=1.577599 μm, λ=1.578487 μm, and λ=1.57937 μm, respectively. In this structure, the channel spacing is about 0.88nm.

Radius of rods is another important parameter which affects on characteristic of the filter. In this part, we investigate changing the radius of the whole rods on the resonance wavelength and drop signal. The normalized transmission spectra of the structure with three different radii of whole rods are shown in Figure 5c. Figure 5c shows that for, r=0.1a, r=0.105a, and r=0.11a, the resonant wavelengths at port C will be λ=1.567464 μm, λ=1.578487 μm, and λ=1.589666μm, respectively. So as we see, increasing the radius of the whole rods results in shifting the resonant wavelength toward higher wavelengths without significant change in the dropping efficiencies values and with channel spacing of 11 nm.

Figure 5. Normalized transmission spectra of the proposed T-shaped CDF at port C for different values of (a) refractive indices of the whole rods (n), (b) refractive indices of the inner rods (nin), (c) radii of the whole rods (r), (d) radii of the inner rods (rin)

Figure 5d shows the normalized transmission spectra at port C for different radii of the inner rods, r_in=0.1a, r_in=0.105a, and r_in=0.11a, respectively. As shown in Fig. 5d, it is obvious that when the radius of inner rods increases, the resonant wavelength shifts toward higher wavelengths without significant change in the dropping efficiencies values. The obtained output wavelengths are λ=1.575827 μm, λ=1.578487 μm, and λ=1.581155 μm, respectively, with channel spacing of 2.6 nm.

5. Conclusions

This paper attempted to present a novel structure for T-shaped channel drop filter using two dimensional photonic crystal ring resonator. The dropping and coupling efficiency of this structure was found to be 100%, with quality factor of 502. The total footprint of the filter is 189.66 μm², which makes it suitable for application in photonic integrated circuits. Afterward, we analyzed the effect of varying different parameters on the resonant wavelength and drop signal. Our numerical simulations reveal the dependence of the CDF’s transmission spectrum on different parameters such as refractive index, radius of inner and whole rods, which means that this structure is tunable for desired wavelengths.

ACKNOWLEDGEMENTS

This work was supported by the Ministry of Higher Education and Scientific Research of Algeria.