K. S. Shivakumar Aradhya 1, Mrityunjay R. Doddamani 2
1KCK Engg Consultancy & Services, A2-345 RMV Clusters, Phase I, Lottegolla Halli, RMV II Stage P.O., Bangalore, India
2Dept. of Industrial and Production Engineering, Gogte Institute of Tech., Belgaum, India
Correspondence to: K. S. Shivakumar Aradhya , KCK Engg Consultancy & Services, A2-345 RMV Clusters, Phase I, Lottegolla Halli, RMV II Stage P.O., Bangalore, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper presents the results of investigations carried out to evaluate the mechanical properties in particular the strain hardening behavior of SiC/Ti-6Al-4V MMC-System. An extensive parametric study was carried out considering the effects of fiber volume fraction, fiber orientations and operating temperature levels on the mechanical properties. Two-dimensional finite element modeling techniques were used in the study adopting the front-end commercial software ANSYS with its nonlinear analysis capabilities. The strain hardening behavior curves generated will form as a useful material database for design engineers engaged in the design of structures made of Metal Matrix Composites (MMCs). The results obtained agree closely with the published works.
Keywords:
Metal Matrix Composite, SiC/Ti-6Al-4V MMC-System, Mechanical Properties, Finite Element Method
Cite this paper: K. S. Shivakumar Aradhya , Mrityunjay R. Doddamani , Characterization of Mechanical Properties of SiC/Ti-6Al-4V Metal Matrix Composite (MMC) using Finite Element Method, American Journal of Materials Science, Vol. 5 No. 3C, 2015, pp. 7-11. doi: 10.5923/c.materials.201502.02.
1. Introduction
The word “composite” in composite material signifies that two or more materials that are combined on a macroscopic scale to form a useful material. A structural composite is a material system consisting of two or more phases on a macroscopic scale, whose mechanical properties are designed to be superior to those of the constituent materials acting independently. The constituents retain their identities in composites, i.e., they do not dissolve or otherwise merge completely into each other although they act in concert. The properties of a composite material mainly depend on properties of their constituents, their geometry & distribution of the phases. One of the most important parameters is the volume fraction of reinforcement, or fiber volume ratio. The distribution of reinforcement determines the homogeneity or uniformity of the material system. The geometry and orientation of reinforcement affect the anisotropy of the system.The mechanical behavior of Metal Matrix Composites (MMCs) has been considered to be the most important in structural design. The mechanical behavior can be divided approximately into two groups. They are the basic mechanical behavior at room temperature and that in the severe environments (e.g. high temperature) in which they operate. The understanding of mechanical behavior under operating environmental conditions is much more essential for a stable design of composite structures. The stress-strain curve of a typical continuous fiber MMC consists of three distinct stages, the first, second and third. In the first stage both the matrix and fiber deform elastically; in the second stage the matrix deforms plastically while the fiber remains elastic; and then both matrix and fiber deform plastically in the third stage of the stress-strain curve. The existence of the second and third stages of the stress-strain curve of MMC depends on the types of the matrix and fiber, and also on the environmental condition under which the mechanical tests to obtain the stress-strain curves are conducted. Most of MMC composite systems, however, appear to possess the first and second stages.In the case of short fiber MMCs, the stress-strain curves do not have three distinct stages. The stress-strain curves of these composites can be divided into two classes. In the first class there is a distinct linear region in the initial portion of the stress-strain curve corresponding to the first stage in the continuous fiber composites, followed by a parabolic stress-strain curve, corresponding to third stage in the continuous fiber composites. The second class of fiber metal matrix composites has stress-strain curves which have no detectable initial region; their stress-strain curves are parabolic in shape over entire stress-strain range.Following is a brief account of analytical and experimental investigations carried out by different investigators to study the influence of fiber volume fraction and temperature levels on the mechanical behavior of composite systems.Saigal and Berry [1] used finite element method to study the effect of volume fraction of silicon particles on localized yielding and crack initiation stress in Aluminum-silicon alloy. They found that increase in volume fraction decreases the stress required for localized yielding, reduces the individual stress concentration magnitude and hence in the stress required for crack initiation for given particle size and shape.Levy and Papazian [2] have investigated the tensile properties and composite stress-strain behavior of aluminum matrix composites containing SiC whiskers using finite element analysis. Two finite-element models were constructed and used for elastoplastic analysis. They observed the addition of SiC increases the elastic modulus, yield strength, ultimate tensile strength and work-hardening rate. In case of transverse-loading, effect of misalignment lowers the composite’s Young’s modulus and work-hardening rate.Aradhya and Surappa [3] predicted the tensile properties of 6061 Al-SiCp particle composites for different volume fractions of SiCp. The particle size was assumed to be 40 μm. They found that below a certain critical volume fraction of SiCp the matrix of the composite yields at slightly lower stresses compared to unreinforced material. The model developed by them predicts the increase in fracture stress of composite due to incorporation of SiCp.Vuorinen and Schwarz [4] used a resonant ultrasound spectroscopy technique to measure the elastic constants of transversely isotropic SiC/Ti-6Al-4V from 10° to 300°K. The composite had 50% volume of SiC fibers imbedded in a Ti-6Al-4V matrix. They used the Varshni equation to fit the temperature dependence of the elastic constants and the engineering moduli. They found that the temperature causes decrease in the Young and shear engineering moduli.Zeng, Peters and Tanaka [5] conducted push-out experiments in the temperature range from room temperature to 530C on SCS-6/Timetal 834. On the basis of the measured maximum load to break the fiber/matrix bond and the load to overcome frictional shear stresses, finite element analysis was performed to derive the strength for the different test temperatures. They found that the material properties decrease with increasing test temperatures.Sun, Chen, Sha and Koop [6], made an extensive work to predict the nonlinear stress-strain curves. Simple tension tests were performed on SCS-6/Ti-6-4 metal matrix composite. A one-parameter plasticity model was used to characterize the elastic-plastic properties i.e. the nonlinear stress-strain behavior. They found that the uniaxial stress-strain relations for specimens with small off-axis angles (less than about 15°) are basically linearly elastic. They also found that the strains of 90° -specimen are small and 45° -specimen yields the largest strain.Thus the experimental and analytical investigations carried out by different researchers have shown that the mechanical behavior of MMCs strongly depend on volume fraction, morphology of reinforcements, operating temperature levels etc. In the present investigation the strain hardening behavior of SiC/Ti-6Al-4V MMC-System is evaluated using Finite Element techniques. A parametric study is carried out considering the effects of fiber volume fraction, fiber orientations and operating temperature levels on the strain hardening behavior. The front-end commercial software ANSYS [7] with its nonlinear analysis capabilities is used in the present study. The results obtained agree closely with the published ones [6].
2. Details of Investigation
The different investigations carried out on SiC/Ti-6Al-4V MMC-system can be grouped under three cases:Case 1: Evaluation of strain hardening behavior at room temperature conditions by varying the fiber volume fraction (10% to 60% in steps of 10%) and loading along fiber direction.Case 2: Evaluation of strain hardening behaviour at elevated temperature (427°C) conditions by varying the fiber volume fraction (10% to 60% in steps of 10%) and loading along fiber direction.Case 3: Evaluation of strain hardening behaviour at a constant fiber volume fraction of 40% at room temperature conditions and by varying the fiber angle from 0° to 90° in steps of 15°.
3. Geometry and Dimensions of Test Coupons
The geometry and dimensions of the test coupon used for investigations under Cases 1 and 2 is depicted in Fig. 1. The coupon has a size of (1000 μm x 1000 μm) with unit thickness. The dimensions ‘a’ and ‘b’ correspond to matrix and fiber widths respectively which are suitably adjusted to get different volume fractions. The test coupon is loaded along fiber directions and investigated under plane stress conditions using nonlinear static analysis approach.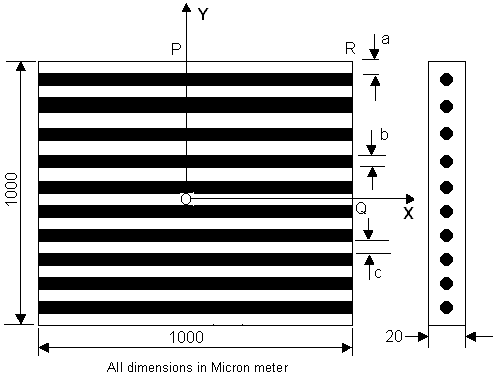 | Figure 1. Geometry and Dimensions of the test coupon used for investigations under Case 1 and Case 2 |
Figure 2 depicts the geometry and dimensions of the test coupon used for investigations under Case 3. The coupon has again a size of (1000 μm x 1000 μm) with unit thickness. The matrix and fiber widths are suitably adjusted to get the desired volume fraction of 40%. The angle θ corresponds to the angle between fiber and loading directions. The test coupon is loaded as shown in Fig. 2 and investigated under plane stress conditions using nonlinear static analysis approach at different fiber angles θ.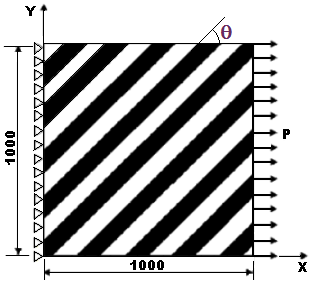 | Figure 2. Geometry and Dimensions of the test coupon used for investigations under Case 3 |
In all the three cases the applied stress levels were gradually increased from zero to the ultimate stress level taking it through the plastic yield point. The large deformation effects were activated and at lower applied stress levels smaller sub-steps (up to 20) were used and at higher applied stress level the sub-steps were increased up to 100 for convergence [7].
4. Material Properties
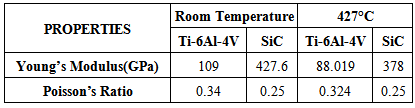
Table 1 gives the details of the material properties of the matrix (Ti-6Al-4V) and fiber (SiC) at room temperature and elevated temperature (427C) conditions respectively. The true stress-strain curves for the matrix and the fiber are shown in Fig. 3. Table 1. Material Properties of SiC\Ti-6Al-4V Composite System
 |
| |
|
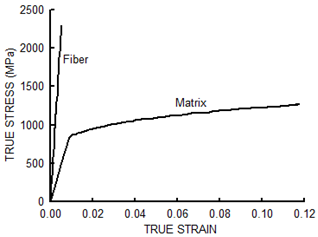 | Figure 3. True stress-strain curves for the matrix and fiber at room temperature conditions |
5. Finite Element Modeling and Analysis
Details of FEM modeling & analysis are as follows:
5.1. FEM Modeling
The model considered under Cases 1 & 2 has a special feature called “Quarter Symmetry Condition” in FEM analysis [7]. This allows the investigator to analyze only one quarter of the model and get the complete behavior of the entire model thus considerably reducing the computational time and efforts. Hence the Quarter Symmetry condition is used advantageously in the current investigation and the FEM modeling details with this condition applied is shown in Fig. 4. Figure 5 shows the FEM mesh for the Quarter Symmetry model with relevant loading and boundary conditions where σ is the applied stress. To improve the accuracy of the results a finer mesh density is used, which was arrived at through a convergence study. Following is the summary of the FEM mesh used:Type of Element: PLANE 42; No. of Elements: 10000;No. of Nodes: 10201; No. of degrees of freedom: 20402 | Figure 4. Quarter Symmetry Model used for analysis under Case 1 & 2 |
 | Figure 5. FEM Mesh for the Quarter Symmetry Model |
The model considered under Case 3 does not have any special feature (as in the previous cases) and hence the complete model is considered for analysis. The FEM modeling details for this case are shown in Fig. 6 with relevant loading and boundary conditions where σ is the applied stress. Following is the summary of the FEM mesh used: Type of Element: PLANE 42; No. of Elements: 448; No. of Nodes: 553; No. of degrees of freedom: 1106 | Figure 6. FEM Mesh for the Case 3 Model |
5.2. FEM Analysis
The FEM analyses were carried out as per the details provided under Sections 2 and 3 using the front-end commercial software ANSYS [7] using its static nonlinear analysis capabilities. The materials properties presented in Sec. 4 were employed in the investigations.
6. Results and Discussion
The results obtained are presented in Figures 7 to 10. Figure 7 shows the stress-strain behavior obtained at room temperature conditions (Case 1). The stress-strain behavior obtained at elevated temperature conditions (427C) is shown in Fig. 8 (Case 2). The stress-strain behavior obtained for 40% volume fraction (at room temperature conditions) for loading at different fiber angles is shown in Fig. 9 (Case 3). A comparison of present results with the published ones [6] is shown in Fig. 10. The comparison corresponds to part of results for Case 1 (Volume fraction: 40%; Room temperature conditions; and Strain varying from 0 to 0.01).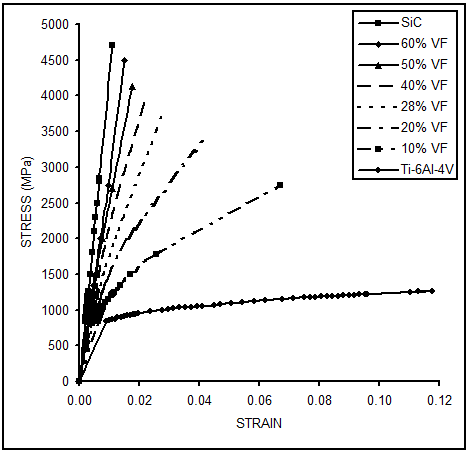 | Figure 7. Stress-strain behaviors for varying fiber volume fractions at Room Temperature |
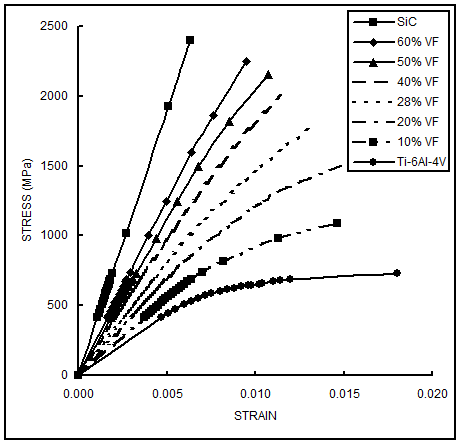 | Figure 8. Stress-strain behavior for varying fiber volume fractions at Elevated Temperature (427C) |
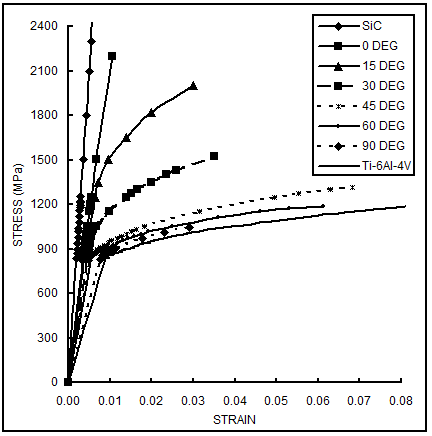 | Figure 9. 6 Stress-strain behaviors for 40% fiber volume fraction with Varying Fiber Angles at Room Temperature |
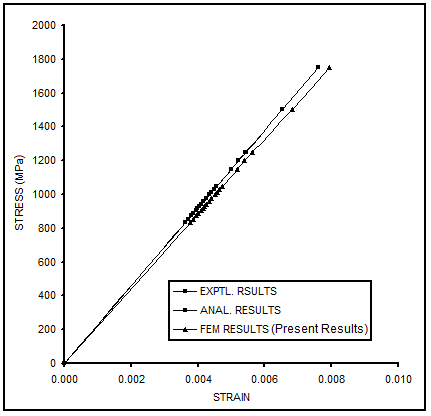 | Figure 10. Comparison of present results with Analytical and Experimental Solutions for 40% fiber volume fraction at room temperature |
7. Conclusions
The following important conclusions can be drawn from the results obtained.• From the stress-strain behavior at room temperature conditions, one can note that with the increase in fiber volume fraction, the stiffness of the composite system increases. The yield strength and ultimate tensile strengths also increase.• Above 40% fiber volume fraction the stress-strain behavior becomes almost linear.• The stress-strain behavior of the composite system at elevated temperature of 427°C exhibits a similar nature as that found at room temperature conditions. • From the stress-strain behavior for Case 3 one can note that at higher fiber angles, the stress-strain behavior tends to follow the characteristics of monolithic titanium, and, at lower fiber angles, the stress-strain behavior tends to follow the characteristics of monolithic silicon carbide. In other words as the fiber angle increases from 0° to 90° the stiffness, yield strength and ultimate tensile strength exhibit a decreasing trend.• Further, from Case 3 results one can see that loading at 45° fiber angle produces the largest strain (≈ 0.068) and loading at 90° fiber angle produces the smallest strain (≈ 0.01).• The FEM results obtained show a good agreement with the published experimental and analytical solutions.
References
| [1] | Saigal, A. and Berry J. T., 1985, “Study of the Effects of Volume Fraction, Size and Shape of Silicon Particles on Mechanical Properties in Al-Si Alloys Using Finite Element Method”, AFS Transactions, pp. 699-704, Vol. 94. |
| [2] | Levy, A., and Papazian, J.N., 1990, ‘Tensile Properties of Short Fiber Reinforced SiC/Al Composites: Finite-Element Analysis’, Metallurgical Transactions A, 21A, pp. 411-420. |
| [3] | Aradhya, K.S.S., and Surappa, M.K., 1991, ‘Estimation of Mechanical Properties of 6061 Al-SiCp Composites Using Finite Element Method’, Scripta METALLURGICA et MATERIALIA, Vol. 25, pp. 817-822. |
| [4] | Vourien, J.E., and Schwarz, R.B., 2000, ‘Elastic Constants of Ti-6Al-4V/SiC Unidirectional Continuous Fiber Composite between 10 & 300K’, Jl. of Composite Materials, Vol. 36 No. 02, pp. 173-182. |
| [5] | Zeng, W.D., Peters, P.W.M., and Tanaka, Y., 2002, ‘Interfacial bond strength and fracture energy at room and elevated temperature in titanium matrix composite (SCS-6/Timetal 834)’, Jl. of Composites, Part A, Vol. 33, pp. 1159-1170. |
| [6] | Sun, C.T., Chen, J.L., Sha, G.T., and Koop, W.E., 1990, ‘Mechanical Characterization of SCS6/Ti-6-4 Metal Matrix Composite’, Jl. of Composite Materials, Vol. 24, pp. 1029-1059. |
| [7] | ANSYS 5.4 – 1997 SAS IP (ANSYS, Inc) Microsoft windows help, ANSYS system help. |











 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML