1. Introduction

The autonomic nervous system (ANS) or autonomic function plays a major role in controlling and regulating the function of the human body. This identifies a crucial need for studies to reveal how it functions in order to understand its status. However, assessment of the ANS is challenging, because the autonomic structure is located far inside the body making it difficult to access directly [1]. In response to this difficulty, Heart Rate Variability (HRV) (i.e., the variation over time of the period between consecutive heartbeats) has been proposed as a promising assessment tool [2]. In order to investigate the relationship of the ANS and HRV, the Autonomic Function Test (AFT) was designed, so that observation could be performed [1, 3].

Like most biological signals, HRV is recognised as a non-stationary signal, where the frequency content of the signal varies over time. However, techniques previously designed for HRV during an AFT have been relatively inefficient, due to the assumption that HRV is a local stationary signal.

To overcome the problem raised by this misassumption, time-frequency approaches have been suggested. Time-Frequency (TF) analysis provides time-localised spectral information for a non-stationary signal, as a distribution function in terms of time and frequency [4]. This technique allows for the analysis and characterisation of different HRV changes in response to the AFT.

Time-Frequency Distribution (TFD) has been used in medical and clinical research to represent HRV [5-6] in time-frequency domain. For HRV during AFT, a few studies have been conducted that implemented TFD as their processing method. However, the use of TFD is different for every application; therefore, the best TFD that is able to characterise HRV needs to be selected. One study [7] compared four TFDs; Smoothed Pseudo Wigner-Ville Distribution (SPWVD), Short-Time Fourier Transform (STFT), Choi-Williams Distribution (CWD), and Discrete Wavelet Transform (DWT), to represent HRV, in response to both physical activities and an AFT [7]. From their visual observation, the SPWVD method is able to provide a high-resolution representation of the signal in both time and frequency. Another related study by [8] showed that the Choi-William Distribution (CWD) demonstrated the best graphical results and indexes during a Valsalva Manoeuvre; when compared with two other TFDs; Wigner Distribution (WD) and Spectrogram [8]. Recently, the Modified-B Distribution (MBD) was proven as a promising TFD to represent HRV, because it was able to produce high TF resolutions and was effective in cross-terms reduction for slowly varying frequency like HRV [9-10].

Since there is no TFD that can be accurately applied to all applications, the TFDs performance comparison needs to be carried out. As we can see, previous performance evaluations [7] and [8] are subjective, using visual comparison. This comparison method might be inaccurate because it is only based on visual observation and provides no quantitative data to be able to prove the reliability of the results. Therefore, in this study we will investigate and compare previously used TFD methods for AFT; i.e., SP, SPWVD, CWD, WD, and MBD, to identify the optimal TFD that characterises the changes of HRV during an AFT in terms of cross-terms reduction, TF resolution and number of TF components, by using a quantitative performance measure [11].

2. Method

2.1. Data Acquisition

Electrocardiography (ECG) was recorded from 32 healthy participants (21 females) with no history of cardiovascular or neurological diseases. Sampling frequency was set up to Fs = 600Hz. The participants were non-smokers and not receiving any medication. The recording session was setup between 8.00am and 12.00pm. Participants were instructed not to consume heavy meals for at least three hours before testing, and were asked to refrain from ingesting beverages containing caffeine and alcohol.

During the session, participant was first asked to lie down and relax for ten minutes. ECG was then recorded for five minutes in the supine position. Next, participant was instructed to stand upright and ECG was recorded for another five minutes in the standing position. Next, participant was asked to lie down again and relax for ten minutes. A further baseline ECG measurement was then taken for five minutes. Participants then immersed their left hand [12] into a 0-5°C water bath (to wrist level) for three minutes, followed by removal of the hand from the water, drying, and a continuation of the ECG recording for another five minutes [13].

The recorded ECG signals from each test were segmented into three minute periods in order to have a standard length of signal. The signals were then processed to quantify the HRV. The 50Hz power line interference was removed using a 2^nd order Butterworth notch filter. The QRS waves were then detected using Pan and Tompkin’s algorithm. This method was chosen, because it was previously proven to detect 99.3% of adult QRS using the MIT/BIH database [14]. The R-R interval was resampled at 4Hz. The resultant HRV is shown in Figure 1. More information on these processes can be found in [15].

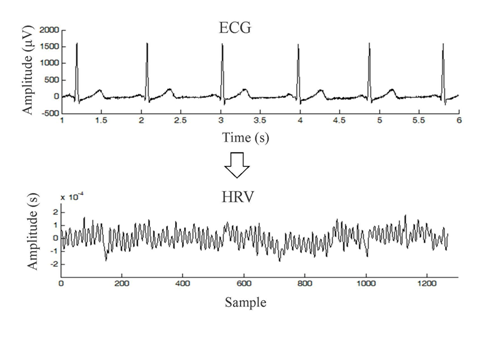Figure 1. The resultant HRV quantified from the ECG signal

2.2. Time-Frequency Distribution

In previous studies, several TFDs had been used to map the HRV from a time domain into a time-frequency domain. The choice of a suitable TFD depends on the application and signal characteristic of the studied signal. Quadratic TFD is one of the most popular classes of TFDs currently being used [4]. Quadratic TFD is based on estimating the instantaneous power spectrum of the signal, using a bilinear operator. The general equation for a quadratic TFD, is [4]:

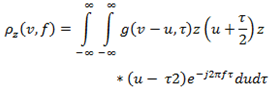(1)

Where, z(t) is the analytic associate of the real signal s(t). The function g(v,τ) is known as the time lag kernel, and determines the characteristics of the TFD. In this study, time-frequency analysis is focused on five generally used TFDs in AFT application. The investigated TFDs are explained below [4]:

2.2.1. Wigner Ville Distribution (WVD)

WVD is the fundamental quadratic TFD [4], whose kernel filter is:

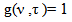(2)

2.2.2. Smoothed Pseudo Wigner Ville Distribution (SPWVD)

This TFD is improvised design of WVD and has a separable kernel expressed as:

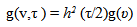(3)

where the window g(v) is the smoothing window and the h(τ) is the analysis window. These two windows were chosen to suppress spurious peaks and to obtain a high TF resolution.

2.2.3. The Choi William Distribution (CWD)

CWD has a 2D Gaussian kernel filter given by:

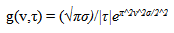(4)

The CWD has one parameter, σ which, controls the sharpness of the 2D filter cut-off.

2.2.4. Spectrogram (SP)

SP has a kernel filter that is represented as:

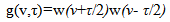(5)

It performs a local or ‘short-time’ Fourier analysis, by using a sliding analysis window w(v) to segment the signal into short sections centred near to the observed time t before computing the Fourier transformation.

2.2.5. Modified B-Distribution (MBD)

MBD is one of the TFDs that can present a high TF resolution for a slowly varying signal such as HRV. The kernel for MBD is

(6)

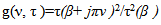where β is a real, positive number between 0 and 1 that controls the trade-off between components’ resolution and cross-terms suppression [16].

2.3. Performance Measure

The performance of the resulting TFDs was compared using an objective quantitative measure criterion expressed as:

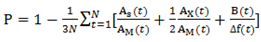(7)

Where for a pair of signal components at time t, A_s is the average of the components sidelobe amplitude relative to average of the components mainlobe amplitude A_M, A_X is the in-between components cross-terms amplitude, and B is the average of the components mainlobe bandwidth relative to ∆f, frequency separation between the components instantaneous frequencies [17]. The aim of this computation is to achieve the best resolution of the signal components. One study [18] has shown how this performance measure is used to optimise TFDs parameters and select best-performing TFDs for artificial, multicomponent signals.

In order to better discriminate TFDs performances for a real life signal, a modification to the measure M was proposed [17-18]. However, they [17-18] used bird signal in their comparison. Study [19] which implemented the proposed measure also used the bird signal in their study while a latest study done by [20] used simulated HRV signal. The present study therefore will apply the proposed modified measure M on the real HRV signal. For selection of the overall optimum TFD, averages of each condition (supine, stand, baseline, cold pressor and recovery) were computed. Group differences in performance measure M for each TFD were explored using ANOVA.

3. Result and Discussions

All five positions from 32 participants - 160 data points were computed for the optimisation process. The computation was conducted using MATLAB software. ANOVA revealed a significant main effect of TFD method, F (4) = 517.15, p < .001, η² = .93. There was no significant effect of condition between participants in different TFDs. The summary of this effect is presented in Figure 2. From this, MBD was significantly different to all other TFDs, p<0.001 except SPWVD (p = .36). In Figure 2, it can be seen that MBD and SPWVD are significantly higher than the other TFDs.

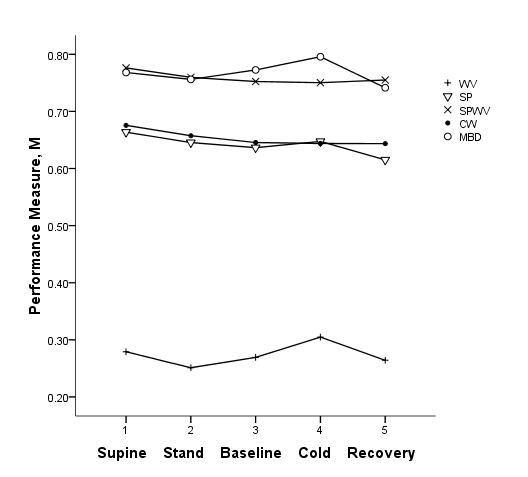Figure 2. Mean performance measure, M at five different conditions (supine, stand, baseline, cold pressor and during recovery) across five different TFD methods

Figure 3 presents the time-frequency plot of optimised TFDs of HRV signal. The left plot shows the time-domain of the HRV, the bottom shows the spectral component and the middle one is the TF representation of the HRV. In Figure 3(a) which represents the WVD of the HRV, the dominant frequency content was observed in both LF and HF. However, this distribution is difficult to interpret due to the presence of interference terms also known as cross-terms, which is the result of the quadratic nature of the transformation. The improvised TFD of WVD which is SPWVD is displayed in Figure 3(b). The figure shows that the crossterm was eliminated whilst retaining the desirable properties of WVD with the hamming window of length 333. In Figure 3(c), CWD with its kernel parameter σ = 0.7848 has been found to represent the HRV with no cross-terms. However, both LF and HF components were smeared which was caused by the synchronization effects prevailing, due to the trade-off between the suppression of cross-terms and auto-component terms. The result shown in Figure 3(d) is almost similar where the SP, known to lack in time resolution smears the TF components. The quadratic SP smoothes away all interference terms and therefore causing the side effect of reducing signal component’s resolution. Figure 3(e) represents the time-frequency plot of MBD with its kernel parameter β = 0.001. From the figure, we can see that there are no cross-terms observed and the plot shows good quality of time-frequency resolution. Among the studied TFDs, MBD and SPWVD demonstrated better time-frequency resolution compared to WVD, CWD and SP. This effect was expected since the value of performance measure, M for both TFDs were very close. From this analysis, MBD and SPWVD are suggested as suitable TFDs that are able to characterise the changes of HRV during AFT in time frequency plot.

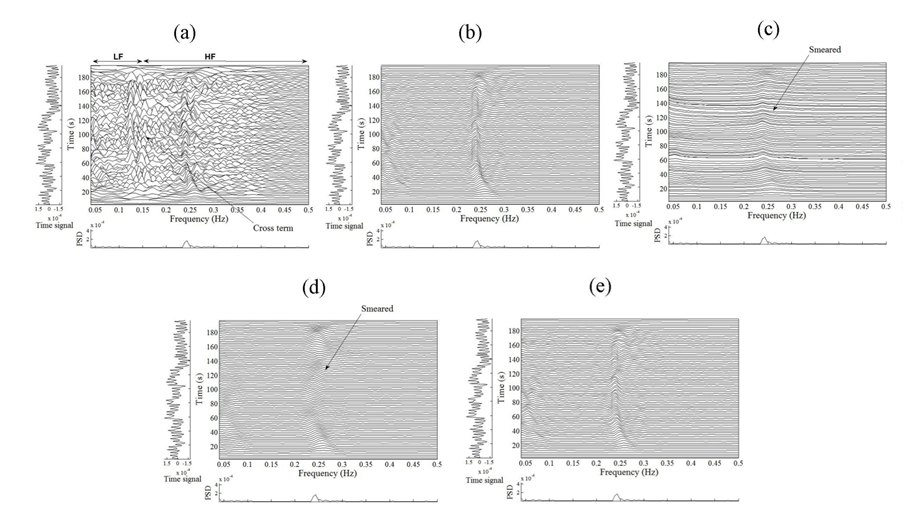Figure 3. TFD of HRV signal during hand immersion in cold water: (a) WVD, (b) SPWVD, (c) CWD, (d) SP, and (e) MBD

4. Conclusions

This study investigated and compared previously used Time Frequency Distribution (TFD) methods (i.e., SP, SPWVD, CWD, WD and MBD) to represent HRV during an Autonomic Function Test (AFT) using a quantitative performance measure. Among the five different types of TFD discussed, Modified-B Distribution (MBD) and Smoothed Pseudo Wigner Ville Distribution (SPWVD) outperformed other TFDs in terms of time-frequency resolution, cross-term suppression and number of time frequency components. Thus, this study proposes MBD and SPWVD as suitable TFDs that are able to characterise the changes of real life HRV during AFT in time frequency plot. Future research will focus on the feature extraction of Heart Rate Variability (HRV) utilising the proposed TFDs. These features then will be used in a wide scale of study such as in autonomic functioning and cardiovascular reactivity testing.

ACKNOWLEDGEMENTS

This study is supported under a project funded by Research University Funding, Universiti Teknologi Malaysia (R.J130000.7845.4F473).