-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2015; 5(3B): 94-99
doi:10.5923/c.jmea.201502.19
Static Characteristics of Two-Axial Groove Journal Bearing Operating on TiO2 Nanolubricant
K. Yathish 1, K. G. Binu 1, Rolvin S. D’silva 1, B. S. Shenoy 2, R. Pai 3
1Department of Mechanical Engineering, St Joseph Engineering College, Vamanjoor, Mangalore, Karnataka, India
2Department of Aeronautical and Automobile Engineering, Manipal Institute of Engineering, Manipal, Karnataka, India
3Department of Mechanical & Manufacturing Engineering, Manipal Institute of Engineering, Manipal, Karnataka, India
Correspondence to: K. Yathish , Department of Mechanical Engineering, St Joseph Engineering College, Vamanjoor, Mangalore, Karnataka, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
A modified Krieger-Dougherty viscosity model is used in conjunction with classical two dimensional Reynolds equation to obtain theoretical steady state performance characteristics of two-axial groove journal bearing operating on TiO2 nano-particle dispersed engine oil. The modified Reynolds equation is non-dimensionalised and solved numerically by finite difference method satisfying the Reynolds boundary condition. A computational code is developed using MATLAB to simulate the bearing characteristics at different eccentricity ratios and volume fractions of TiO2 nanoparticle additives. Results reveal a significant improvement in load carrying capacity, hydrodynamic pressure distribution, and oil side leakage for two-axial groove journal bearing operating on TiO2 based nano-oil as compared to plain oil.
Keywords: Hydrodynamic journal bearing, Krieger-Dougherty viscosity model, TiO2 nanoparticles, Reynolds equation, Load carrying capacity, Oil side leakage
Cite this paper: K. Yathish , K. G. Binu , Rolvin S. D’silva , B. S. Shenoy , R. Pai , Static Characteristics of Two-Axial Groove Journal Bearing Operating on TiO2 Nanolubricant, Journal of Mechanical Engineering and Automation, Vol. 5 No. 3B, 2015, pp. 94-99. doi: 10.5923/c.jmea.201502.19.
Article Outline
1. Introduction
- Nanotechnology is poised to bring in revolutionary changes across all spheres of modern life. It is playing an important role in all fields, starting from medicine, manufacturing, defence, and education. Over the last two decades, nano-technology has found a place in tribology with focus on thin film lubrication and also with nanoparticle lubricant additives. Nanoparticles are used as lubricant additives to base oil and these additives play an important role in enhancing the tribological properties of base oil. Considering the scarcity of energy to be prevalent in the days to come, it is necessary to minimise losses due to friction and wear. One of the application of lubricants is in support mechanisms, where journal bearing, being one of the most popular support mechanism used in high load and high speed applications, experiences wear of its surfaces and frictional loss. In the present days nanolubricants are being used in hydrodynamic journal bearings and their application is on the rise.Over the last few years, many tribologists have been focus-sing on the effect of nanolubricant in hydrodynamic journal bearing. In general, under low loading, the losses due to friction and wear are negligible on contact surfaces. But under heavy loading, the lubricant film generated between the bearing and journal will be intensely squeezed, and may not be able to protect contact surfaces. Some researches revealed that nanoparticle additives enhance the supporting forces [1]. Therefore, friction and wear can be reduced by adding nanoparticle to the lubricant. Many studies have been carried out to study the properties of nanolubricant and their application in the past decade. Various types of nanoparticles have been used as lubricant additives and their performance in thin film lubrication have been studied [2-9]. All these studies showed reduced wear and friction in tribo-surfaces with the use of nanoparticle lubricant additives. However, there is a major gap in research regarding theoretical simulation of nanolubricant in fluid film bearing. Available literature suggests improvement in static and dynamic performance characteristics by considering only variable viscosity analysis of nanoparticle additive [10-12]. However viscosity variation with increasing lubricant additive concentration needs to be studied with.In this study, the influence of lubricant viscosity variation, due to increasing concentrations of nanoparticle additives, on the static characteristics of a journal bearing operating on TiO2 based lubricant is presented. The viscosity variations has been studied and modelled over the past many decades. Einstein [13] developed the first viscosity model for dilute concentration (ϕ=0.01) of spherical particles in 1956.and it is expressed in equation-1. Later it was extended by Brinkman [14] and then by Batchelor [15] and it is expressed in equation-2 and equation-3 respectively. In this paper, Modified Krieger-Dougherty viscosity model have been employed to predict the relative viscosities of nanolubricant for varying nanoparticle concentrations. The predicted viscosities are then used in the computations of load carrying capacity of two-axial groove journal bearing. The classical Reynolds equation for fluid film lubrication is modified to incorporate relative viscosities of nanoparticle dispersions. The modified equation is solved numerically using finite difference scheme to obtain the pressure profiles for various volume fractions of TiO2 nanoparticle dispersions. The load carrying capacity is then computed and compared with results for plain oil.
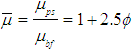 | (1) |
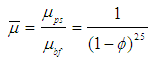 | (2) |
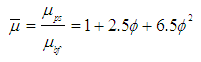 | (3) |
2. Theoretical Analysis
2.1. Governing Equations for Journal Bearing
- The governing equation for hydrodynamic journal bearings is the two-dimensional classical Reynolds equation for an incompressible fluid. It is written as:
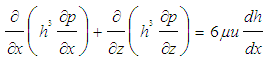 | (4) |
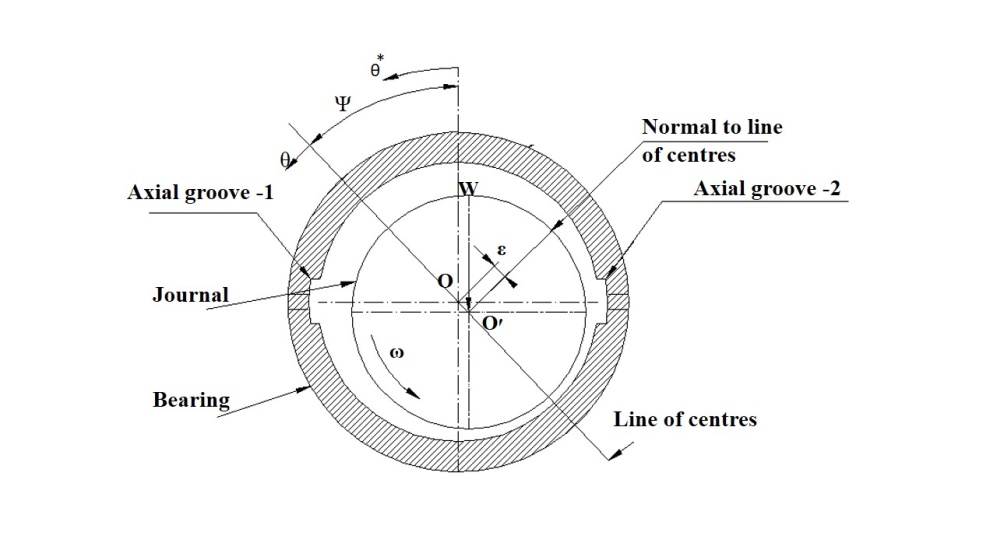 | Figure 1. Two-axial groove Journal bearing configuration |
 | (5) |
 The non-dimensional Reynolds equation thus obtained is of the form,
The non-dimensional Reynolds equation thus obtained is of the form,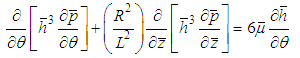 | (6) |
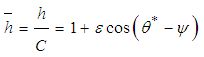 | (7) |
2.2. Solution Methodology
- The non-dimensional Reynolds equation, presented as equation-6, is solved numerically using finite difference method.A rectangular grid is employed and the central difference scheme of discretization is used to numerically formulate the equation. Gauss-Siedel with SOR method is employed for numerical solution. A computer program is developed in MATLAB to calculate all the bearing characteristics at different eccentricity ratio. An illustration of the grid employed is shown in Figure 2.
 | Figure 2. Grid point notation for film extent |
 . The boundary conditions could then be expressed as,
. The boundary conditions could then be expressed as, at
at  and
and 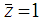 at the grooves [16]
at the grooves [16]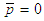 at
at 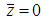 and
and 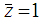 , or all nodes other than nodes in the grooves.The boundary conditions as applied to the journal bearing are illustrated in Figure 3.
, or all nodes other than nodes in the grooves.The boundary conditions as applied to the journal bearing are illustrated in Figure 3.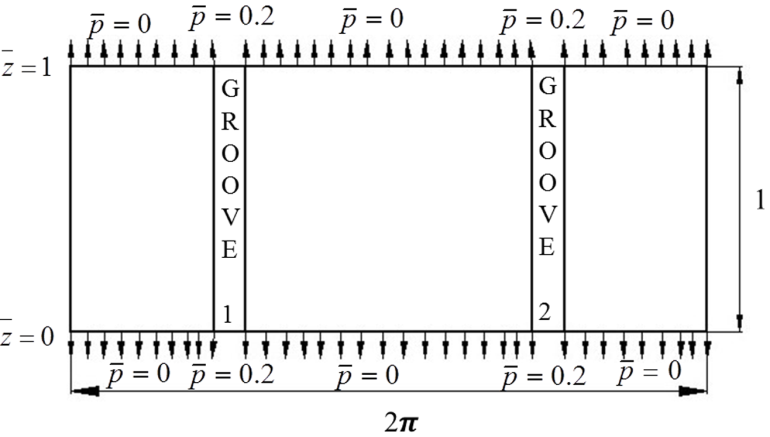 | Figure 3. Illustration of Reynolds boundary condition applied to grooved journal bearing |
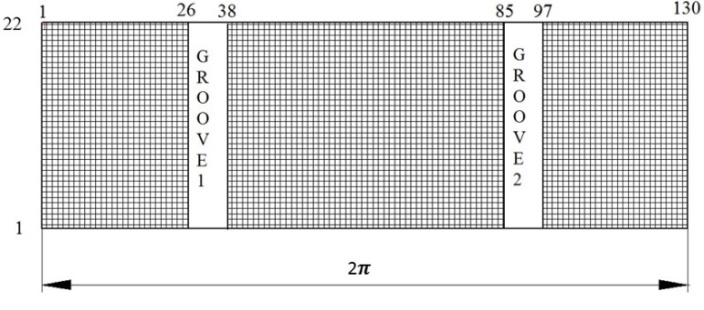 | Figure 4. Mesh size and groove nodes |
2.3. Nanofluid Viscosity Model
- The Krieger–Dougherty equation for shear viscosity of particle dispersions [17] was presented in 1959 covering the full range of particle volume fractions. It was of the form:
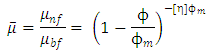 | (8) |
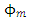 is the maximum particle packing fraction, which is approximately 0.605 at high shear rates [18] and η is the intrinsic viscosity, whose typical value for mono disperse suspensions of hard spheres is 2.5 [18, 22]. Equation-8 was later modified by Chen et al. [19] to consider the packing fraction within the particle aggregate structure. The modified Krieger–Dougherty equation thus takes the form of equations presented below:
is the maximum particle packing fraction, which is approximately 0.605 at high shear rates [18] and η is the intrinsic viscosity, whose typical value for mono disperse suspensions of hard spheres is 2.5 [18, 22]. Equation-8 was later modified by Chen et al. [19] to consider the packing fraction within the particle aggregate structure. The modified Krieger–Dougherty equation thus takes the form of equations presented below: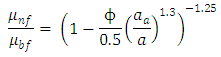 | (9) |
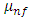 = Viscosity of nanofluid dispersion,
= Viscosity of nanofluid dispersion,
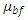 = Viscosity of Base oil SAE-30.Binu et al [20] has reported the value of aa/a for TiO2 based nanolubricants as 7.77, based on DLS particle size analysis, and used it in modified Krieger–Dougherty viscosity model to study the effects of nanoparticle aggregation on viscosity of nanolubricants and it was validated experimentally with rheological tests. In line with this, the present study also employs the packing fraction aa/a as 7.77. The viscosity values are then used in the modified Reynolds equation to obtain the static characteristics.The non-dimensional modified Reynolds equation for variable viscosity is derived and is presented in the form given below:
= Viscosity of Base oil SAE-30.Binu et al [20] has reported the value of aa/a for TiO2 based nanolubricants as 7.77, based on DLS particle size analysis, and used it in modified Krieger–Dougherty viscosity model to study the effects of nanoparticle aggregation on viscosity of nanolubricants and it was validated experimentally with rheological tests. In line with this, the present study also employs the packing fraction aa/a as 7.77. The viscosity values are then used in the modified Reynolds equation to obtain the static characteristics.The non-dimensional modified Reynolds equation for variable viscosity is derived and is presented in the form given below: 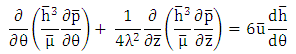 | (10) |
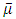 = μ/μ0. The values of
= μ/μ0. The values of 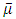 is computed in the Matlab code using the modified Krieger-Dougherty model provided in equation-9.
is computed in the Matlab code using the modified Krieger-Dougherty model provided in equation-9.2.4. Steady State Characteristics
2.4.1. Load Carrying Capacity
- The load carrying capacity of hydrodynamic journal bearing is obtained by integrating the pressures along the journal surface. Simpson’s 1/3 rule is used to perform the integration. The components of the load along and perpendicular to the line of centres are obtained as follows:
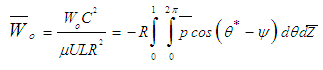 | (11) |
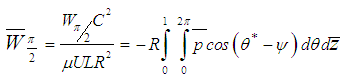 | (12) |
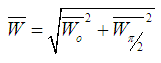 | (13) |
2.4.2. Attitude Angle
- The calculation of attitude angle is performed using
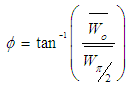 | (14) |
2.4.3. Side Leakage
- The total side flow of lubricant is calculated from the formula:
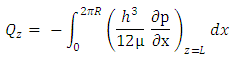 | (15) |
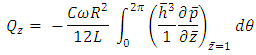 | (16) |
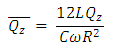 | (17) |
3. Results and Discussions
3.1. Validation of Computational Code
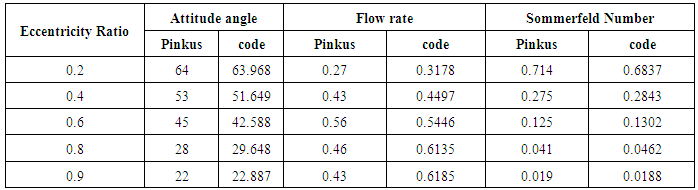
- Validation of static characteristics of a two axial groove journal bearing has been done in comparison with the standard published values of Pinkus [21]. The MATLAB code generated values are compared with published values of Pinkus [21] and it is given in Table 1.
|
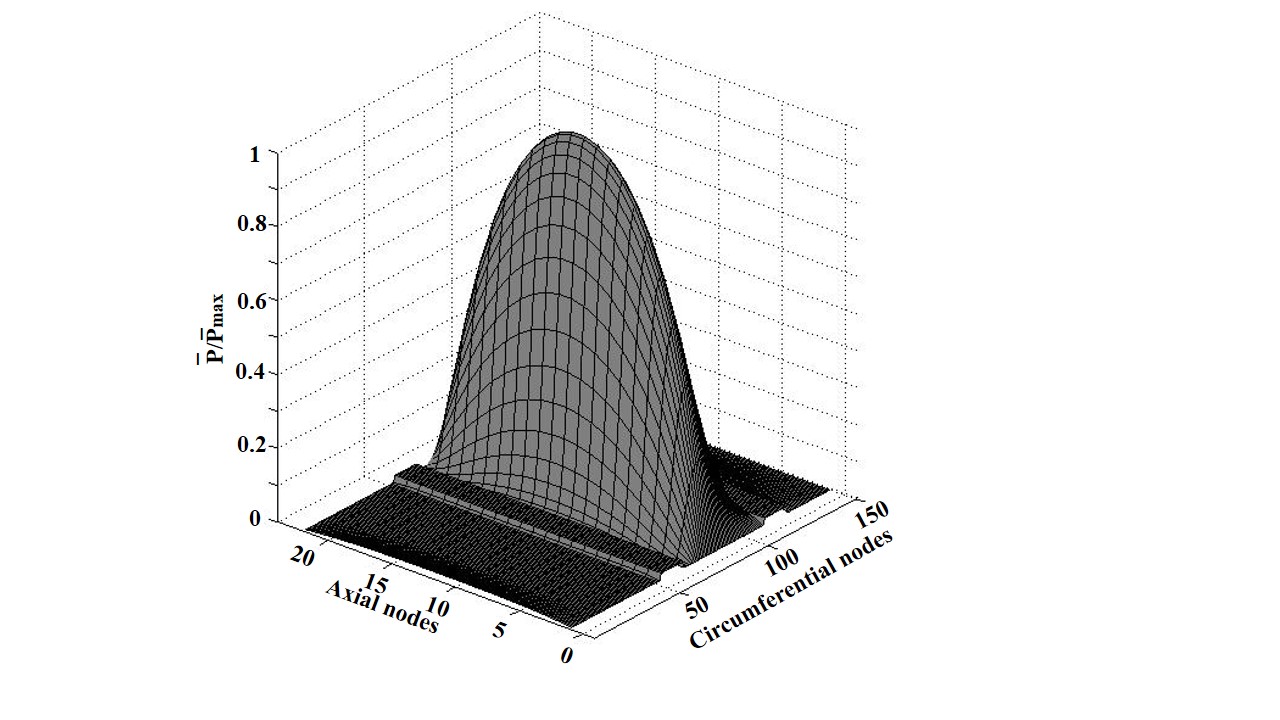 | Figure 5. Pressure distribution for 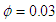 and and 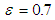 |
3.2. Hydrodynamic Pressure Profiles
- Figure. 6 shows the pressure distribution plot for different additive concentration at the bearing mid-plane. The ratio of non-dimensional pressure to maximum pressure was obtained for an eccentricity ratio of ε=0.7 and additive concentrations ranging from 0.001 to 0.05 volume fraction.
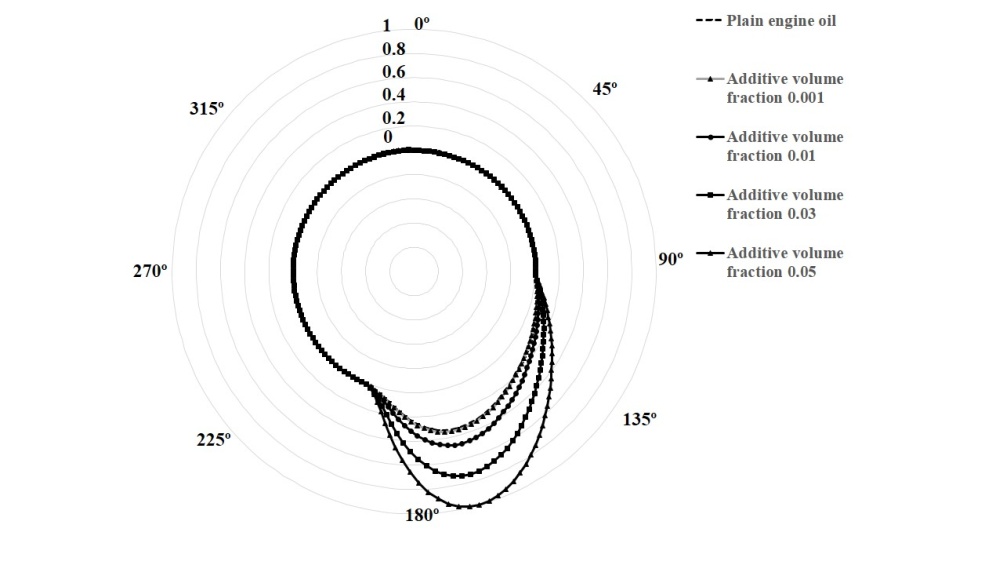 | Figure 6. Comparison of non-dimensional pressures for different TiO2 nanoparticle concentrations at an eccentricity ratio of ε=0.7 |
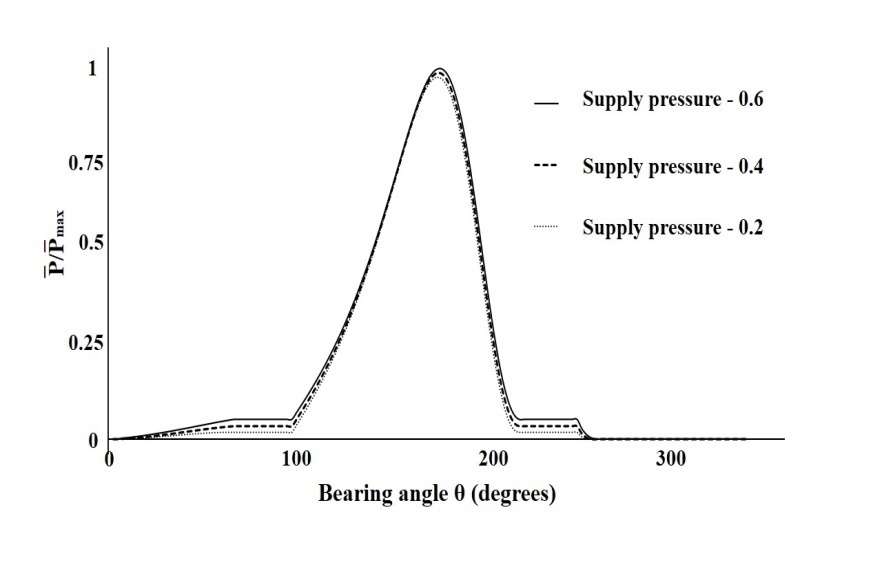 | Figure 7. Comparison of non-dimensional pressures for different supply pressure at an eccentricity ratio of ε=0.7 |
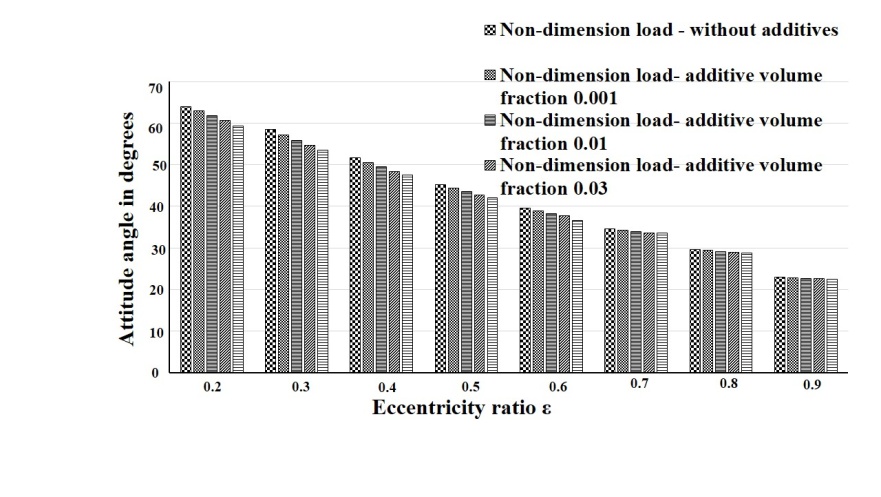 | Figure 8. Comparison of attitude angle for different TiO2 nano-particle concentrations and eccentricity ratio |
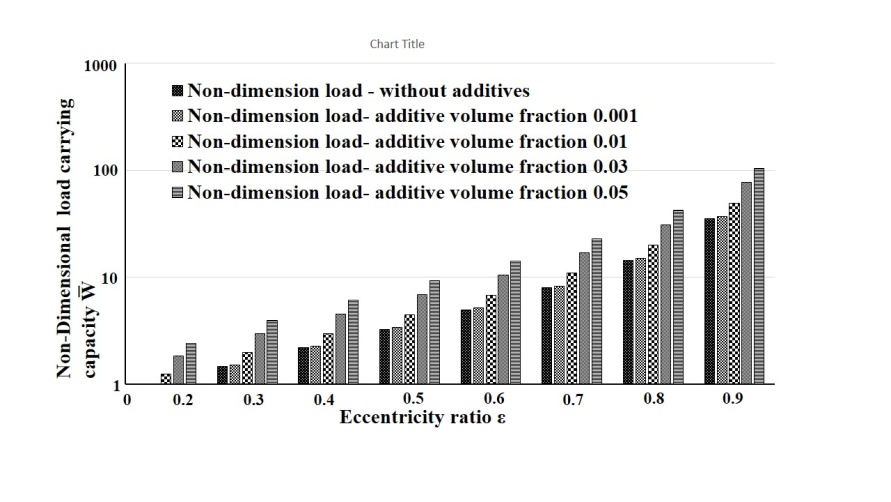 | Figure 9. Comparison of load carrying capacities at different TiO2 nanoparticle concentrations |
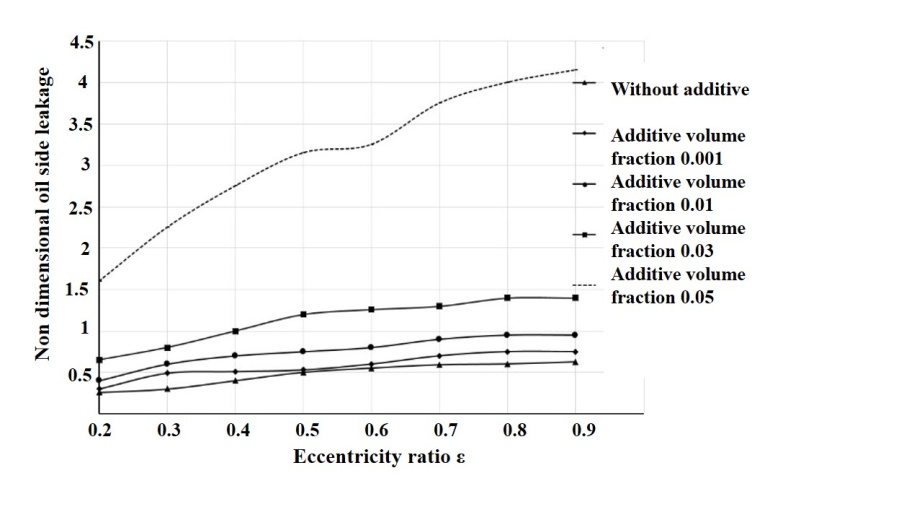 | Figure 10. Comparison of Oil side leakage at different TiO2 nano-particle concentrations |
4. Conclusions
- The influence of TiO2 nanoparticle lubricant additives on the static performance characteristics of two-axial groove hydrodynamic journal bearing is theoretically simulated using modified Krieger-Dougherty viscosity model. The study reveals an increase in load carrying capacity of 40%, in comparison to plain engine oil for journal bearings operating on nanolubricant containing TiO2 nanoparticle additives at a concentration of 0.01 volume fraction. The attitude angle and oil side leakage also shows good results with increasing TiO2 nanoparticle concentrations. Further experimental studies are however needed to understand better the effect of lubricant additives.
ACKNOWLEDGEMENTS
- The first, second and third authors would like to acknowledge The Management, St Joseph Engineering College, Mangalore for supporting their research.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML