Saviraj A. S. , Sunil Kumar S. , Vinay D. R.
Department of Mechanical Engineering, Mangalore Institute of Technology and Engineering, Moodabidri, India
Correspondence to: Saviraj A. S. , Department of Mechanical Engineering, Mangalore Institute of Technology and Engineering, Moodabidri, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The study of buckling behaviour of tubular structures has been an intriguing area of research in the field of solid mechanics. Unlike the global Euler buckling of slender structures under compressive loads, tubular structures deform with their walls buckling as individual simply supported plates. The buckling mode of these tubes depends on several factors such as the material properties, the length of the tube, the cross-sectional shape and the edge conditions. This paper investigates the effect of aspect ratio and thickness on the elastic buckling response of equilateral triangular tubes through a series of numerical simulations performed using MSC PATRAN/NASTRAN 2011. The results obtained from numerical simulations are compared with theoretical results and previously published work in the literature. The critical loads predicted by finite element simulations are in good agreement with experimental results and theoretical values.
Keywords:
Aspect ratio, Wall thickness, Buckling factor, Critical load, Thin-Walled structures, Angle section
Cite this paper: Saviraj A. S. , Sunil Kumar S. , Vinay D. R. , Elastic Buckling Response of Equilateral Triangular Tubes under Uni-Axial Compression, Journal of Mechanical Engineering and Automation, Vol. 5 No. 3B, 2015, pp. 19-22. doi: 10.5923/c.jmea.201502.04.
1. Introduction
The buckling behaviour of thin-walled tubular structural members with regular (equiangular and equilateral) convex polygonal cross-sections (RCPS) has been an important area of study in the field of solid mechanics. This is mainly because of their widespread applications in various fields including aeronautical, marine and civil engineering. For instance, the applications of these members in the construction industry range from communication towers, lighting posts and transmission line structures, to rail road sign frames and railway overhead contact line posts. Thin-walled metal tubes with different cross-sections are widely used as energy absorbing structural components in high-volume industrial products such as cars, trains and ships. The benefit of thin-walled structures stems from their low weight, low cost and ease of production. The post buckling properties of tubes to form plastic folds and absorb the kinetic energy in a crash, plays an important role in the design of crash safety structures in automobiles. Buckling factor (k) and critical buckling load (Pcr) are important parameters for thin walled tubular structures and several studies have been conducted to predict them. The buckling mode of these tubes depends on several factors such as the material properties, the length of the tube, the cross-sectional shape and the edgeconditions. It has been postulated in [2–4] that the buckling of a tubular or structure can be related to the behaviour of the individual walls of the structure under compressive loads.The present paper aims to examine the effect of aspect ratio and thickness on the elastic buckling response of equilateral triangular tubular structures subjected to uni-axial loading. The approach adopted is based on the recently developed formulation for critical buckling load by Arka P. Chattopadhyay et al. [7] based on new assumptions and redefined boundary conditions.Section 2 presents the fundamental equations for the elastic buckling response of triangular tubes under uniform compression and summarizes the conclusions presented in [7] concerning the calculation of buckling factor and critical load. Section 4 is devoted to the investigation of the effect of varying aspect ratio on the critical buckling load of the equilateral triangular tubes whereas section 5 addresses the influence of the wall thickness on the same. Finally the paper closes with some concluding remarks (Section 6).Throughout the paper, results obtained from finite element analysis performed with MSC NASTRAN/PATRAN 2011 are presented and discussed. For validation purposes, these results are compared with the results extracted through theoretical analysis and previously published experimental results.
2. Theoretical Buckling Phenomenon of Triangular Tubes
The following fundamental equations for equilateral triangular tube subjected to uni-axial loading are extracted from [7]. The critical load is given by,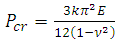 | (1) |
Where 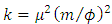 is the buckling factor and µ is a parameter expressed as,
is the buckling factor and µ is a parameter expressed as,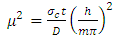 | (2) |
where m is the number of half sine waves formed along the height of the tube and D is the flexural rigidity of the tube.From Eq. (1) the transitional aspect ratios are 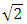 for m=1 to m=2,
for m=1 to m=2,  for m=2 to m=3,
for m=2 to m=3, 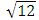 for m=3 to m=4 and so on.
for m=3 to m=4 and so on.
3. Numerical Simulation
The goal of these simulations is to examine the effect of aspect ratio and thickness on the elastic buckling response of equilateral triangular tubes under uni-axial compression. In particular an in-depth study on the influence of the aspect ratio and wall thickness on the variation of the critical buckling load is presented in the Sections 4 and 5. Simulations were performed on a series of angle structures representing the angle sections of equilateral tubes. Simulations were carried out using MSC/PATRAN software. The angle sections were modelled with constant wall length of 50 mm. Material properties were assigned to the geometries with Young’s modulus E of 210 GPa and Poisson’s ratio ν of 0.3. The material properties used in the simulation study represents Q235 Steel. Type of simulation was purely elastic buckling and thus value of yield strength was not required in the simulation. The models of geometries were meshed using a shell mesh. Quadrilateral elements with four corner nodes per element were used. Every node of the elements had five degrees of freedom, three translations and two rotations. The translations are in the global co-ordinate system while the rotations are about two orthogonal axes defined at each node. The open edges of the angle section were restricted from translatory motion in the out-of-plane direction while rotation about the vertical open edges was allowed. The bottom edge was restrained from moving in all directions and from rotating about the edge; the top edge was restrained from moving along the edge and out of plane directions and from rotating about the edge, but is allowed to move in the loading direction. Fig. 1 shows the meshed angle section with aspect ratio two subjected to boundary conditions and edge pressure of 100 MPa on the top surface. 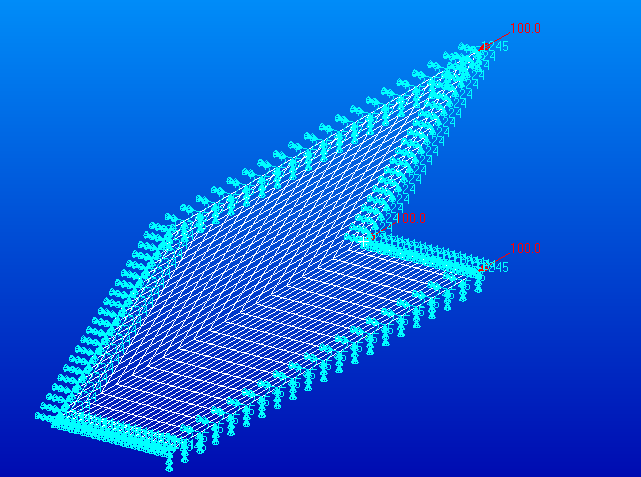 | Figure 1. Meshed angle section with aspect ratiotwo subjected to boundary constraints and edge pressure |
4. Effect of Aspect Ratio on the Critical Buckling Load
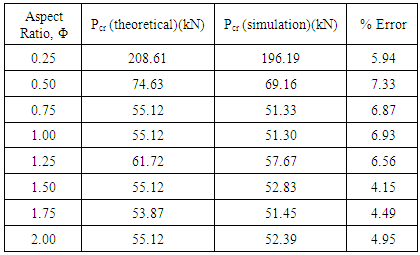
In this section, finite element simulations to examine the effect of aspect ratio on the elastic buckling response of equilateral triangular tubes are presented. Simulations were performed on a series of angle sections with varying aspect ratios. The length l of the main wall was chosen as 50 mm thus making the length of the restraining wall lr equal to 25 mm. The height h was changed for different simulations in order to vary the aspect ratios from 0.25 to 2. The wall thickness t was set to 1 mm. Meshing of the geometries was performed using four noded quadrilateral shell elements of size approximately 0.2 mm. As an example Fig. 2 shows the top view of the exaggerated buckled shape of a model which has an aspect ratio of 1. The total critical load of the section from the simulation of this case was 51.3 kN. The critical load of the structure was calculated theoretically using Eq. (1) as 55.12 kN. This shows good agreement between the simulation and theoretical results with a discrepancy of approximately 6.93% for this aspect ratio. Table 1 shows the values of critical load from the results of simulations and the corresponding theoretical values at certain aspect ratios of the angle section of an equilateral tube with sides equal to 50 mm.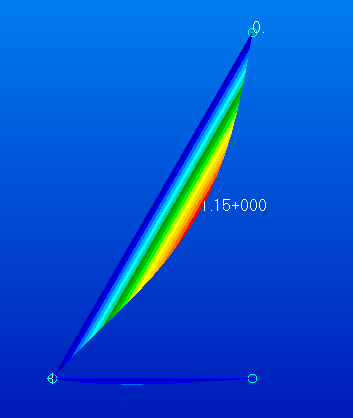 | Figure 2. Top view of buckled shape of angled section with aspect ratio of one |
Table 1. Theoretical and simulation results of critical load of the equilateral triangular tube for varying aspect ratios
 |
| |
|
Theoretical and computational values of Pcr of the angle section were plotted against the aspect ratio of the section. The graphs are presented in Fig. 3. The figure shows good agreement between theoretical results and results of the finite element simulations with a maximum discrepancy of approximately 7.33%. Figure shows the exaggerated scale simulation results of the angle section of an equilateral tube at different aspect ratios varying from 0.25 to 2.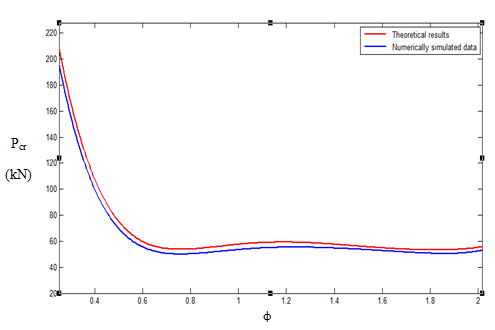 | Figure 3. Comparison of Pcr curves obtained from theoretical and computational results over different aspect ratios |
From Fig. 3 it is evident that critical load decreases significantly with increase in aspect ratio up to an aspect ratio of around 0.5. After that critical load almost remains constant with increase in aspect ratio except for a local maximum at around 1.25, which is the transitional aspect ratio (for m=1 to m=2) as predicted from the theoretical analysis. The figure shows good agreement between theoretical and simulation results.
5. Effect of Wall Thickness on the Critical Buckling Load
In this section, finite element simulations to examine the effect of wall thickness on the elastic buckling response of equilateral triangular tubes are presented. Simulations were performed on a series of angle sections with varying wall thickness. The length l of the main wall was chosen as 50 mm thus making the length of the restraining wall lr equal to 25 mm. The height h was set to 150 mm to produce a constant aspect ratio of 3. The wall thickness t was varied from 1 mm to 2.5 mm to examine the influence of wall thickness on the elastic buckling response of the tube. Meshing of the geometries was performed using four noded quadrilateral shell elements of size approximately 0.2 mm. The validation of the finite element model was made by direct comparison with the established experimental results presented in [8]. As an example Fig. 4 shows the top and isometric views of the exaggerated buckled shape of a model which has a wall thickness of 1 mm. The total critical load of the section from the simulation of this case was 12.03 kN. The critical load of the structure from experimental results was found out to be 11.46 kN. This shows good agreement between the simulation and experimental results with a discrepancy of approximately 4.97% for this wall thickness. Table 2 shows the values of critical load from the results of simulations and the corresponding experimental values at certain wall thicknesses of the angle section of an equilateral tube with aspect ratio equal to three.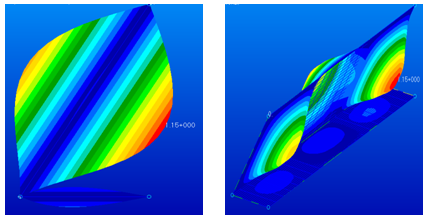 | Figure 4. Top and isometric views of the exaggerated buckled shape of a model with wall thickness of 1 mm |
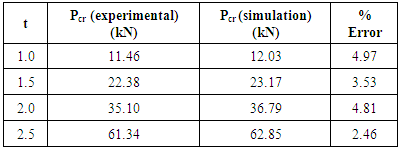
Table 2. Comparison of buckling load from the present method with experimental results (Wu Hong et al. [8]) for varying wall thickness
 |
| |
|
Experimental and computational values of Pcr of the angle section were plotted against the wall thickness of the section. The graphs are presented in Fig 5 from which it is worth noting that critical load increases with the increase in wall thickness. This is because the elastic stiffness of tube increases with its wall thickness. The figure shows good agreement between experimental results and results of the finite element simulations with a maximum discrepancy of approximately 4.97%. 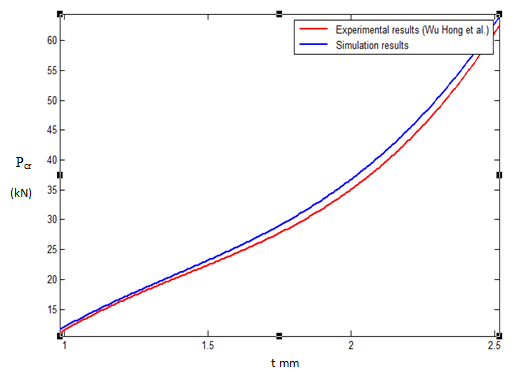 | Figure 5. Comparison of Pcr curves obtained from experimental and computational results over different wall thicknesses |
6. Conclusions
From the above discussions it can be concluded that both aspect ratio and wall thickness of the equilateral triangular tube influences its elastic buckling response, however the effect of latter is more significant. It must be pointed out that discrepancy exists between the numerical simulations and the experiments with the maximum discrepancy being 7.33% for aspect ratio of 0.5 and wall thickness 1 mm. Geometrical imperfections of the tubes cannot be avoided in manufacturing. In numerical simulations, imperfections of the tubes are not included. Difference of the boundary conditions in testes and numerical simulations is another important factor.
References
| [1] | Timoshenko S. P, Gere J. M, (1961), “Theory of elastic stability”, New York, McGraw-Hill, 1969. |
| [2] | Bulson P. S., (1969), “Stability of Flat Plates”, American Elsevier Publication Company, New York, pp. 27, 295. |
| [3] | Eugenio Ruocco, Massimiliano Fraldi, “An analytical model for the buckling of plates under mixed boundary conditions”, Engineering Structures, Volume 38, May 2012, Pages 78-88. |
| [4] | Minoru Yamashita, Manabu Gotoh, Yasuhiko Sawairi, “Axial crush of hollow cylindrical structures with various polygonal cross-sections: Numerical simulation and experiment”, Journal of Materials Processing Technology, Volume 140, Issues 1–3, 22 September 2003, Pages 59-64. |
| [5] | Rodrigo Gonçalves, Dinar Camotim, “Elastic buckling of uniformly compressed thin-walled regular polygonal tubes”, Thin-Walled Structures, Volume 71, October 2013, Pages 35-45. |
| [6] | Gonçalves R, Ritto-Corrêa M, Camotim D. A new approach to the calculation of cross-section deformation modes in the frame work of Generalized Beam Theory. Computational Mechanics 2010;46(5):759–81. |
| [7] | Arka P. Chattopadhyay, Elizabeth Frink, X.J. Xin, Kevin B. Lease, “Elastic buckling characteristics of triangular tubes under uniaxial loading”, Thin-Walled Structures, Volume 52, March 2012, Pages 29-41. |
| [8] | Wu Hong, Fengnian Jin, Jiannan Zhou, Zhicheng Xia, Ying Xu, Lin Yang, Qing Zheng, Hualin Fan, “Quasi-static axial compression of triangular steel tubes”, Thin-Walled Structures, Volume 62, January 2013, Pages 10-17. |
| [9] | A. Alavi Nia, M. Parsapour, “Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections”, Thin-Walled Structures, Volume 74, January 2014, Pages 155-165. |
| [10] | X.W. Zhang, H. Su, T.X. Yu, “Energy absorption of an axially crushed square tube with a buckling initiator”, International Journal of Impact Engineering, Volume 36, Issue 3, March 2009, Pages 402-417. |

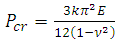
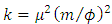 is the buckling factor and µ is a parameter expressed as,
is the buckling factor and µ is a parameter expressed as,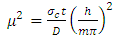
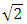 for m=1 to m=2,
for m=1 to m=2,  for m=2 to m=3,
for m=2 to m=3, 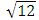 for m=3 to m=4 and so on.
for m=3 to m=4 and so on. 




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
