-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Journal of Mechanical Engineering and Automation
p-ISSN: 2163-2405 e-ISSN: 2163-2413
2015; 5(3A): 26-32
doi:10.5923/c.jmea.201501.05
Entropy Analysis of Combined Heat and Mass Transfer over a Plate Embedded in a Porous Medium
Meisam Habibi Matin
Department of Mechanical Engineering, Kermanshah University of Technology, Kermanshah, Iran
Correspondence to: Meisam Habibi Matin, Department of Mechanical Engineering, Kermanshah University of Technology, Kermanshah, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper the second law analysis for heat and mass transfer over a plate embedded in a porous medium is conducted numerically. The governing continuity, momentum, energy and concentration equations are reduced to ordinary differential equations using similarity transformations. These equations are subsequently solved using an implicit finite difference scheme known as Keller-box method. The numerical data for velocity, temperature and concentration fields are used to compute local entropy generation, total entropy generation and Bejan number. The effects of Reynolds number, Schmidt number, Prandtl number, mass diffusion parameter, and concentration difference parameter on local entropy generation, total entropy generation, and Bejan number are reported.
Keywords: Porous medium, Heat transfer, Mass transfer, Entropy generation
Cite this paper: Meisam Habibi Matin, Entropy Analysis of Combined Heat and Mass Transfer over a Plate Embedded in a Porous Medium, Journal of Mechanical Engineering and Automation, Vol. 5 No. 3A, 2015, pp. 26-32. doi: 10.5923/c.jmea.201501.05.
Article Outline
1. Introduction
- Convective heat transfer over a plate embedded in a porous medium has many applications such as in petroleum production, separation processes in chemical engineering, thermal insulation systems, buildings, and nuclear reactors. In a pioneering paper, Cheng and Minkowycz [1] studied natural convection over a vertical plate with variable surface temperature with the plate embedded in a porous medium. Bejan and Poulikakos [2] investigated free convective boundary layer in a porous medium for non-Darcian regime. The mixed convective flow boundary layer over a vertical plate in porous medium was analysed by Merkin [3]. Kim and Vafai [4] studied the natural convective flow over a vertical plate embedded in porous medium. Chamkha [5] investigated the free convective flow in porous medium with uniform porosity ratio due to solar radiation flux. The MHD mixed convective flow over a vertical porous plate in porous saturated medium and assuming non-Darcian model was studied by Takhar and Beg [6]. Ranganathan and Viskanta [7] investigated the fluid mixed convective boundary layer over a vertical plate embedded in porous medium. They claimed that the viscous effects are significant and cannot be neglected. Kayhani et al. [8] studied the natural convection boundary layer along impermeable inclined surfaces embedded in a porous medium. Chamkha et al. [9] presented a non-similarity solution for natural convective flow over an inclined plate in porous medium due to solar radiation. Forced convection over a vertical plate in a porous medium was studied by Murthy et al. [10] with a non-Darcian model. They showed that the increase of solar radiation flux and also suction causes increase in Nusselt number and heat transfer rate. Kayhani et al. [11] studied local thermal non-equilibrium in porous media due to sudden temperature change and heat generation.The use of second law of thermodynamics to analyze heat and fluid flow in engineering devices and systems has become increasingly important. This approach is driven by the realization among the thermal science community that the systems must be designed and operated so that the degradation of energy or the generation of entropy is minimized. There are various sources for entropy generation in engineering systems. In thermal systems, the main sources of entropy generation are heat transfer, mass transfer, viscous dissipation, electrical conduction, chemical reaction and coupling between heat and mass transfer as discussed by Bejan and co-workers in a series of pioneering publications [12-15]. The study of entropy generation in a liquid film falling along an inclined plate was performed by Saouli and Aїboud -Saouli [16]. Mahmud et al. [17] studied the case of mixed convection in a channel considering the effect of a magnetic field on the entropy generation. Aziz [18] investigated the entropy generation in a plane Couette flow for different boundary conditions at the plates. The effects of magnetic field and viscous dissipation on entropy generation in a falling liquid film were studied by Aїboud -Saouli et al. [19, 20]. Aїboud -Saouli and Saouli [21] conducted entropy generation analysis for viscoelastic MHD flow over a stretching sheet. They showed that the magnetic parameter, Hartman, Reynolds and Prandtl numbers cause the local entropy generation to increase. Rezaiguia et al. [22] investigated the effects of Prandtl and Eckert numbers on the local entropy generation in a forced convection boundary layer flow. They observed that with an increase in Eckert number or a decrease in Prandtl number, the local entropy generation increases. The general formulation for the local entropy generation in an incompressible flow of Newtonian fluid had been given by Hirschfelder et al. [23]. The entropy generation for combined forced convection heat and mass transfer in a two dimensional channel was investigated by San et al. [24].In the present study, the second law analysis for heat and mass transfer over a plate embedded in a porous medium is investigated numerically. To the best of our knowledge, this problem has remained unexplored. The governing continuity, momentum, energy and concentration equations are reduced to ordinary differential equations with similarity transformations. The resulting equations are solved using an implicit finite difference scheme known as the Keller-box method. The local entropy generation is calculated using the numerical derived data for the velocity, temperature and concentration fields in the entropy generation expression derived by Bejan [12]. The total entropy generation is evaluated by integrating the local entropy generation data over the flow domain.
2. Problem Formulation
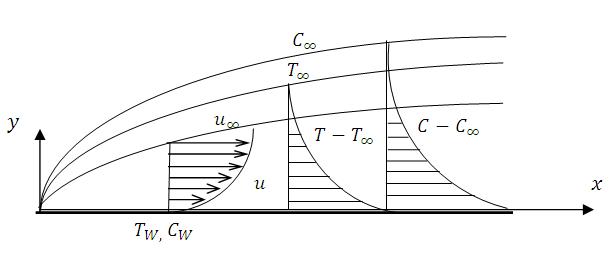 | Figure 1. Schematic of flow model and coordinate system |
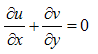 | (1) |
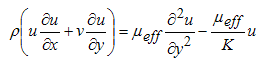 | (2) |
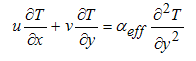 | (3) |
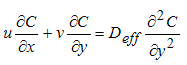 | (4) |
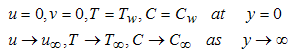 | (5) |
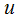 and
and 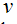 are velocity components in x and y directions, respectively. The symbols
are velocity components in x and y directions, respectively. The symbols 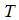 and
and 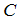 denote temperature and mass concentration at a general location (x, y) in the flow field, respectively. The plate is assumed to be a constant temperature
denote temperature and mass concentration at a general location (x, y) in the flow field, respectively. The plate is assumed to be a constant temperature 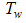 . The diffusing species at the plate have a fixed mass concentration
. The diffusing species at the plate have a fixed mass concentration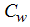 . The quantities
. The quantities 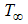 and
and 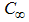 represent the ambient temperature and ambient mass concentration, respectively. Here,
represent the ambient temperature and ambient mass concentration, respectively. Here, 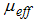 is the effective dynamic viscosity of the fluid,
is the effective dynamic viscosity of the fluid, 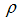 is the fluid density,
is the fluid density, 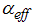 is the effective thermal diffusivity of the medium, and
is the effective thermal diffusivity of the medium, and 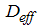 is the effective mass diffusivity of the medium. The assumption that the effective viscosity is identical to dynamic viscosity is appropriate for packed beds of particles, and commonly used to describe boundary layer flows in a porous medium. The following similarity variables are introduced to reduce the governing equations to ordinary differential equations:
is the effective mass diffusivity of the medium. The assumption that the effective viscosity is identical to dynamic viscosity is appropriate for packed beds of particles, and commonly used to describe boundary layer flows in a porous medium. The following similarity variables are introduced to reduce the governing equations to ordinary differential equations: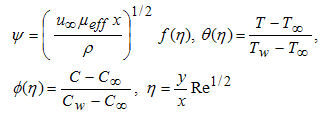 | (6) |
 is defined as
is defined as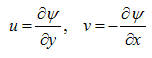 | (7) |
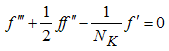 | (8) |
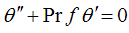 | (9) |
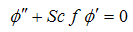 | (10) |
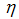 . The boundary conditions take the following form:
. The boundary conditions take the following form: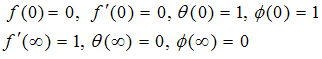 | (11) |
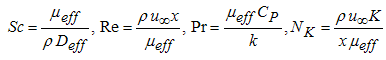 | (12) |
3. Second Law Analysis
- Using the boundary layer approximation, the entropy generation can be simplified as follows
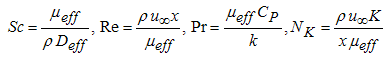 | (13) |
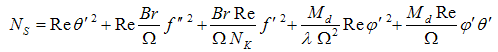 | (14) |
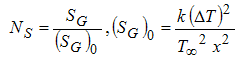 | (15) |
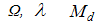 are the dimensionless temperature difference, the dimensionless concentration difference and the mass diffusion parameter, respectively. These three parameters are defined as follows:
are the dimensionless temperature difference, the dimensionless concentration difference and the mass diffusion parameter, respectively. These three parameters are defined as follows: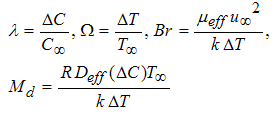 | (16) |
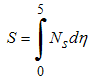 | (17) |
 was found to cover the three boundary layer regions in their entirety. Also, Bejan number was calculated as the ratio of the entropy generation due to heat transfer ST to the total entropy generation S i.e.
was found to cover the three boundary layer regions in their entirety. Also, Bejan number was calculated as the ratio of the entropy generation due to heat transfer ST to the total entropy generation S i.e.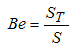 | (18) |
4. Numerical Procedure
- Eqs. 8-11 are solved numerically using an efficient implicit finite-difference scheme known as Keller-box method. The method is implemented in four steps. First, Eqs. 8-10 are reduced to seven first-order differential equations. Second, the equations are discretized using central finite differences. Third, the resulting nonlinear algebraic equations are linearized using Newton’s method [26-28] and written in matrix vector form. The fourth and final step uses the block-tridiagonal-elimination technique to solve the linearized algebraic equations. A step size of Δη = 0.005 was found to satisfy the convergence criterion of 0.001 in all cases. As noted earlier, the choice of
 satisfactorily covered the three boundary layer regions in their entirety.
satisfactorily covered the three boundary layer regions in their entirety.5. Results and Discussion
- Numerical computations were performed to study the effects of various dimensionless parameters on the local entropy generation, the total entropy generation and Bejan number. Figure 2 shows the local entropy generation in boundary layer as function of dimensionless group
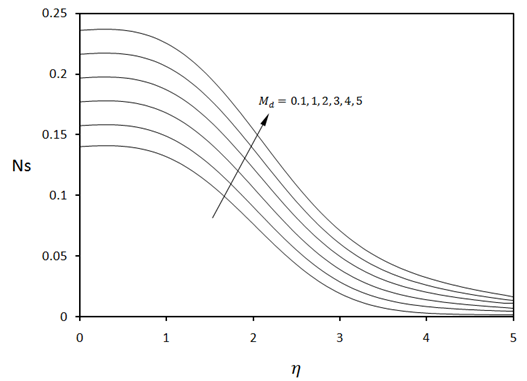
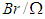 which may be viewed as a measure of viscous dissipation in the flow. The curves in Fig.2 show that the increase in viscous dissipation leads to increase in local entropy generation. Because of large velocity gradients in the region near the plate, this near-plate region generates more entropy compared with that generated in the region far from the plate. As the concentration difference parameter λ is increased, the local entropy generation is reduced as can be seen in Fig.3. Figure 4 shows as the mass diffusion parameter Md increases, the local entropy generation increases. Again, the region near the plate experiences larger entropy genera- tion compared with the region further into the flow field. Fig. 5 illustrates the sensitivity of local entropy generation to Schmidt number Sc. Although the effect of Schmidt number does not appear explicitly in the entropy generation equation (15), its influence on entropy generation is exerted through the velocity, temperature, and mass concentration characteristics which are governed by Eqs. (8-11) which contain Sc.
which may be viewed as a measure of viscous dissipation in the flow. The curves in Fig.2 show that the increase in viscous dissipation leads to increase in local entropy generation. Because of large velocity gradients in the region near the plate, this near-plate region generates more entropy compared with that generated in the region far from the plate. As the concentration difference parameter λ is increased, the local entropy generation is reduced as can be seen in Fig.3. Figure 4 shows as the mass diffusion parameter Md increases, the local entropy generation increases. Again, the region near the plate experiences larger entropy genera- tion compared with the region further into the flow field. Fig. 5 illustrates the sensitivity of local entropy generation to Schmidt number Sc. Although the effect of Schmidt number does not appear explicitly in the entropy generation equation (15), its influence on entropy generation is exerted through the velocity, temperature, and mass concentration characteristics which are governed by Eqs. (8-11) which contain Sc. | Figure 2. Local entropy generation for various values of dimensionless group parameter when 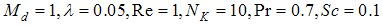 |
 | Figure 3. Local entropy generation for various values of dimensionless group parameter when 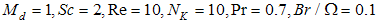 |
 | Figure 4. Local entropy generation for various values of Schmidt number  |
 | Figure 5. Local entropy generation for various values of Schmidt number when 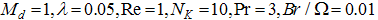 |
 which produces an increase in heat transfer and hence an increase in entropy generation. The effect of permeability parameter NK on local entropy generation is illustrated in Fig.8. For the combination of variables chosen for preparing Fig.8, the local entropy generation decreases only slightly with the increase in the permeability of the medium.
which produces an increase in heat transfer and hence an increase in entropy generation. The effect of permeability parameter NK on local entropy generation is illustrated in Fig.8. For the combination of variables chosen for preparing Fig.8, the local entropy generation decreases only slightly with the increase in the permeability of the medium.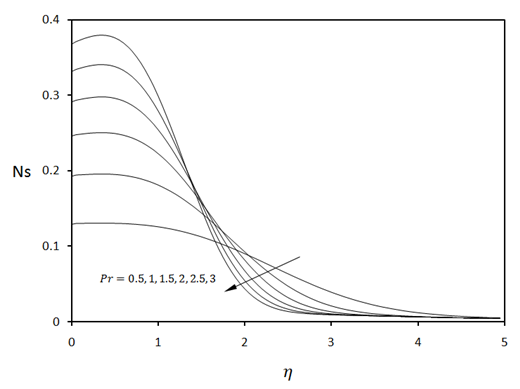 | Figure 6. Local entropy generation for various values of Prandtl number when 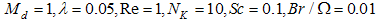 |
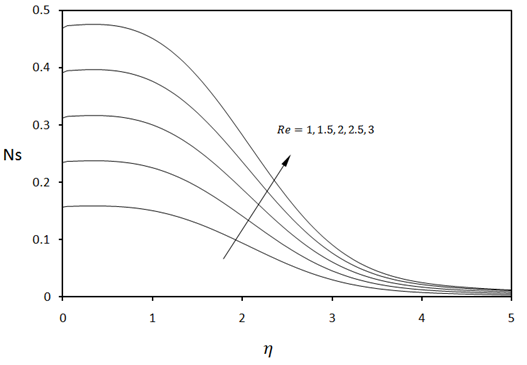 | Figure 7. Local entropy generation for various values of Reynolds number when  |
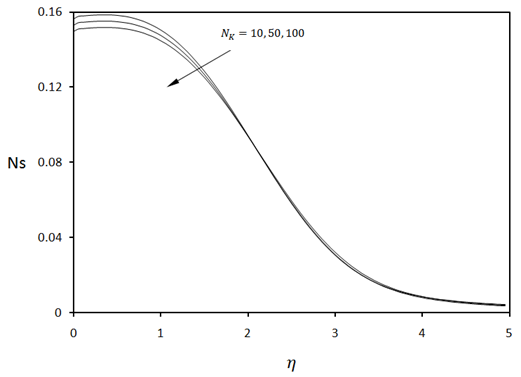 | Figure 8. Local entropy generation for various values of permeability parameter NK when  |
 increases. In other words, a stronger mass transfer process tends to attenuate the total entropy generation slightly. Fig.12 shows that the total entropy generation increases as Prandtl number (and hence heat transfer) increases. However, the increase in permeability of the medium i.e. NK tends to reduce entropy generation slightly.
increases. In other words, a stronger mass transfer process tends to attenuate the total entropy generation slightly. Fig.12 shows that the total entropy generation increases as Prandtl number (and hence heat transfer) increases. However, the increase in permeability of the medium i.e. NK tends to reduce entropy generation slightly.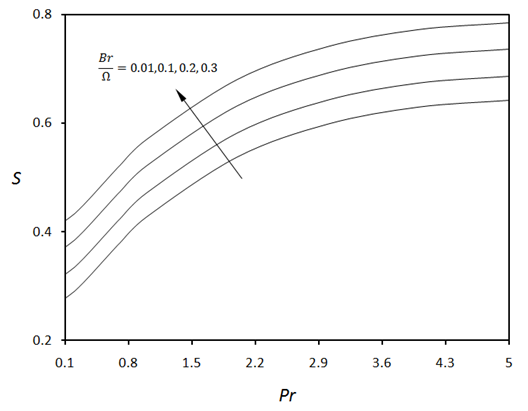 | Figure 9. Total entropy generation versus Prandtl number for various values of dimensionless group parameter when  |
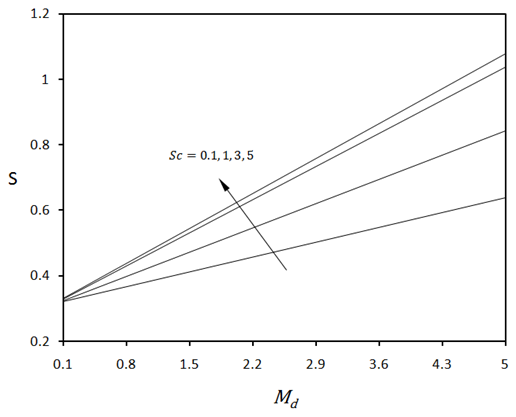 | Figure 10. Total entropy generation versus mass diffusion parameter for various values of Schmidt number when 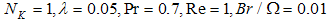 |
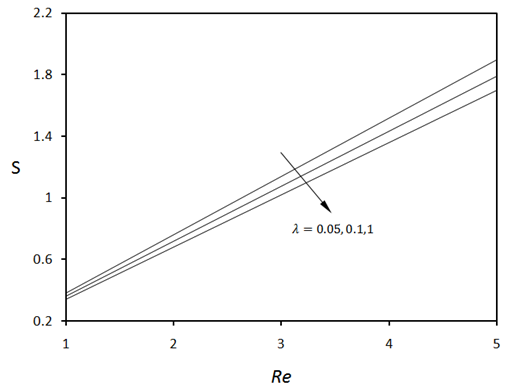 | Figure 11. Total entropy generation versus Reynolds number for various values of dimensionless concentration difference when 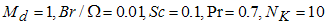 |
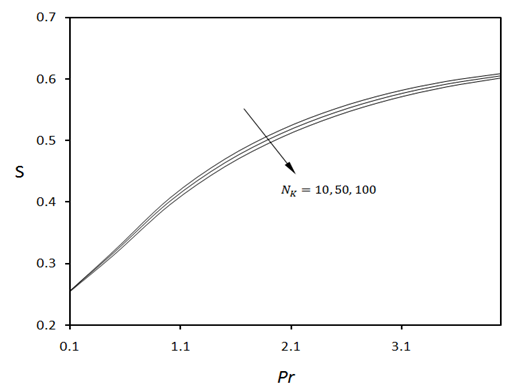 | Figure 12. Total entropy generation versus Prandtl number for various values of permeability parameter when 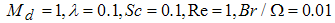 |
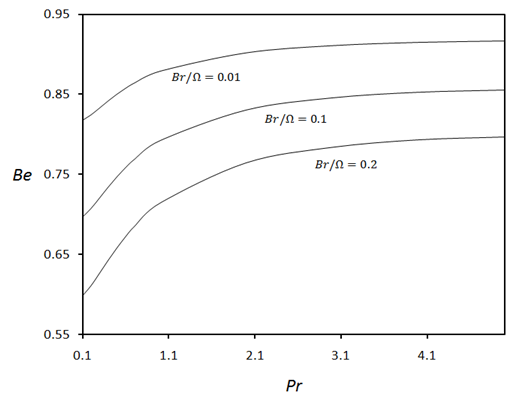 | Figure 13. Bejan number versus Prandtl number for various values of dimensionless group parameter when 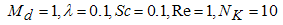 |
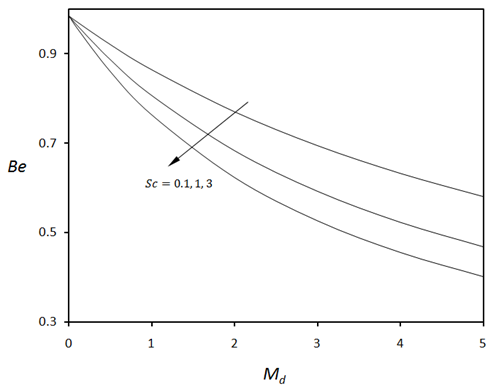 | Figure 14. Bejan number versus mass diffusion parameter for various values of Schmidt number when 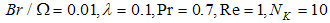 |
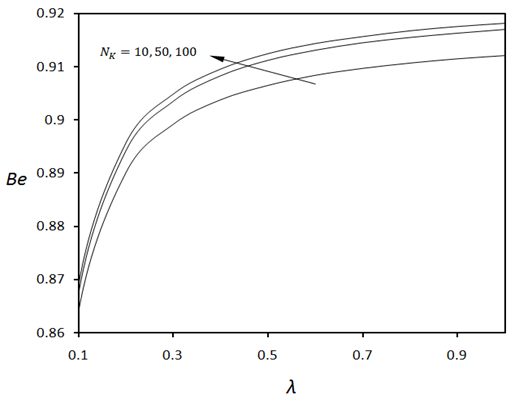 | Figure 15. Bejan number versus dimensionless concentration difference for various values of permeability parameter when 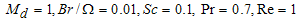 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML