Ryota Hashimoto1, Tomofumi Koyama2, Mamoru Kikumoto3, Toru Saito3, Mamoru Mimura1
1Kyoto University, Kyoto, Japan
2Kansai University, Osaka, Japan
3Yokohama National University, Kanagawa, Japan
Correspondence to: Ryota Hashimoto, Kyoto University, Kyoto, Japan.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Angkor ruin, one of the World Cultural Heritage in Cambodia includes many masonry structures in danger of collapse due to geotechnical problems. The foundation of the Angkor monuments is artificial soil embankment, so-called “rammed earth”, and its compaction quality affects significantly on the stability of the buildings. In this paper, to investigate the influence of the compaction quality of the rammed earth numerically, stability analyses of an actual building in Angkor (Prasat Suor Prat N1 Tower) were performed with NMM-DDA code, which is a discontinuum based numerical method. In order to treat the different mechanical behavior of rammed earth with different density (void ratio), the subloading modified Cam-clay model, a constitutive model for saturated overconsolidated soil, was also applied. The simulations were performed in two cases changing the initial density (void ratio) of the rammed earth, and then, its effect on the stability of the structure was discussed based on the simulation results.
Keywords:
Masonry structure, Angkor, Numerical simulation, NMM-DDA
Cite this paper: Ryota Hashimoto, Tomofumi Koyama, Mamoru Kikumoto, Toru Saito, Mamoru Mimura, Stability Analysis of Masonry Structure in Angkor Ruin Considering the Construction Quality of the Foundation, Journal of Civil Engineering Research, Vol. 4 No. 3A, 2014, pp. 78-82. doi: 10.5923/c.jce.201402.13.
1. Introduction
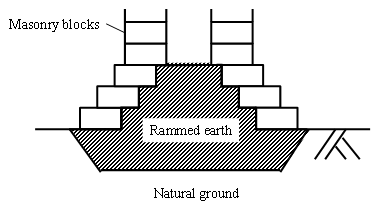
Today, Angkor ruin (JSA [1]), a World Cultural Heritage in Cambodia, contains large numbers of the masonry structures in danger of collapse because of geotechnical problems. For instance, many buildings are tilted due to uneven settlement of the foundation ground as shown in Fig. 1. This uneven settlement is often caused by the structural characteristics of the buildings. Fig. 2 is a schematic figure of the foundation of the Angkor monuments. Masonry blocks are stacked on the artificial soil embankment, so-called “rammed earth”, directly. Hence, the deformation and/or failure of the foundation due to the building self-weight will cause the deterioration of the upper structure immediately. Since the strength and stiffness of rammed earth depend on its quality of compaction significantly, it can be inferred that the construction condition of the rammed earth affect the stability of the structures.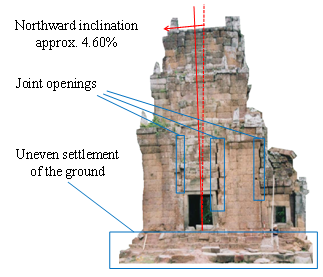 | Figure 1. Prasat Suor Prat N1 Tower in Angkor before restoration (West side view) |
 | Figure 2. Schematic diagram of the foundation in Angkor |
In this paper, to investigate the influence of compaction quality of the rammed earth on the stability of the masonry structure, numerical simulation of Prasat Suor Prat N1 Tower in Angkor (Fig. 1) was carried out using NMM-DDA (Miki et al. [2], Hashimoto et al. [3]), a discontinuum based numerical method. The simulations were carried out for two cases with different initial density (void ratio) of the rammed earth, and the differences between the simulation results were discussed.
2. Basic Theory of NMM-DDA
NMM-DDA is a discontinuum based numerical method which was developed combining NMM (Numerical Manifold Method, Shi [4]) and DDA (Discontinuous Deformation Analysis, Shi and Goodman [5]). Similarly to the original DDA and NMM, the formulation of NMM-DDA is based on the principle so-called the minimization of potential energy (Miki et al. [2]). The total potential energy for the whole system can be expressed as: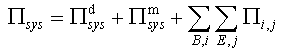 | (1) |
The first and second terms on the right side of Eq. 1 are the potential energy for DDA and NMM parts, respectively (which is exactly same as DDA and NMM alone). The third term represents the potential energy for the contacts between a DDA block i and a NMM element j. Based on Hamilton’s principle, from the stationary condition of Eq. (1), equation of motion in NMM-DDA can be derived as Eq. 2. 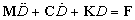 | (2) |
where 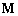 is the mass matrix,
is the mass matrix, 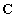 is the viscosity matrix,
is the viscosity matrix, 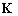 is the stiffness matrix, and
is the stiffness matrix, and 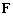 is the external force vector.
is the external force vector. 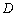 ,
, 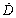 and
and 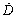 are the displacement, velocity, and acceleration of DDA blocks and the nodes of NMM elements, respectively. In the process of deriving the stationary condition, the first and second terms of the right side in Eq. (1) are minimized in terms of the displacement variables of the DDA blocks (
are the displacement, velocity, and acceleration of DDA blocks and the nodes of NMM elements, respectively. In the process of deriving the stationary condition, the first and second terms of the right side in Eq. (1) are minimized in terms of the displacement variables of the DDA blocks (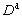 ) and the NMM elements (
) and the NMM elements (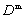 ), respectively same as DDA and NMM alone. The third term, specific to NMM-DDA, is minimized in terms of both
), respectively same as DDA and NMM alone. The third term, specific to NMM-DDA, is minimized in terms of both 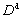 and
and 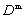 . Consequently, in the formulation of NMM-DDA, only defining the potential energy for the contacts between DDA blocks and NMM elements is newly required. The detailed explanations for the theory of NMM-DDA and derivation of the contact sub-matrixes can be seen in the references (Miki et al. [2]). The original NMM-DDA code treats only linear elastic material, however, elasto-plastic NMM-DDA code was also developed by Hashimoto et al. [3].
. Consequently, in the formulation of NMM-DDA, only defining the potential energy for the contacts between DDA blocks and NMM elements is newly required. The detailed explanations for the theory of NMM-DDA and derivation of the contact sub-matrixes can be seen in the references (Miki et al. [2]). The original NMM-DDA code treats only linear elastic material, however, elasto-plastic NMM-DDA code was also developed by Hashimoto et al. [3].
3. Subloading Modified Cam-Clay Model
To evaluate the deformation/failure processes of the rammed earth, a constitutive model for overconso-lidated soil should be used. Hashimoto et al. [3] introduced the subloading modified Cam-clay model (Hashiguchi [6]), a elasto-plastic model for overconsolidated soil, into NMM-DDA.The yield function of the subloading modified Cam-clay model is expressed as follows: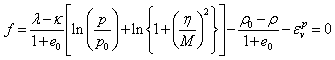 | (3) |
where λ is the compression index, κ is the swelling index, e0 is the initial void ratio, p and p0 are the present and initial mean principal stress, respectively, and 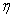 is the stress ratio (=q/p). ρ is the parameter of overconsolidation expressed as follows;
is the stress ratio (=q/p). ρ is the parameter of overconsolidation expressed as follows;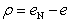 | (4) |
where e is the present void ratio, and eN is the void ratio on Normal Consolidation Line under the same stress condition. Thus, when a soil is in overconsolidated state, 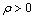 , and in normally consolidated state,
, and in normally consolidated state, 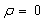 .
. 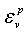 is the plastic volumetric strain. Defining the evolution rule of
is the plastic volumetric strain. Defining the evolution rule of 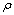 as
as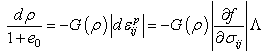 | (5) |
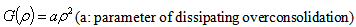 | (6) |
and considering the associated flow rule and Prager’s compatibility equation, elasto-plastic stiffness tensor can be derived.
4. Overview of Prasat Suor Prat N1 Tower
In this study, as an objective of the simulation, Prasat Suor Prat N1 Tower was selected. The N1 Tower is a masonry structure in Angkor which had been in danger of collapse due to geotechnical problems, and the restoration project was conducted by Japanese Government Team for Safeguarding Angkor (JSA) from 2002 to 2005. Outlines of the N1 Tower and damages before the restoration are described below.The N1 Tower consists of the main tower and the antechamber (see Fig. 3). The antechamber faces south and the bathing pond is located to the north of the N1 Tower. The main tower is composed of the platform, three stories (the 1st, 2nd and 3rd) and roof. The main material of the building is laterite blocks and sand stones are partially used. As shown in Fig. 2, the foundation ground of the Tower consists of two parts: natural ground and rammed earth. Natural ground is clayey soil and rammed earth is sandy soil.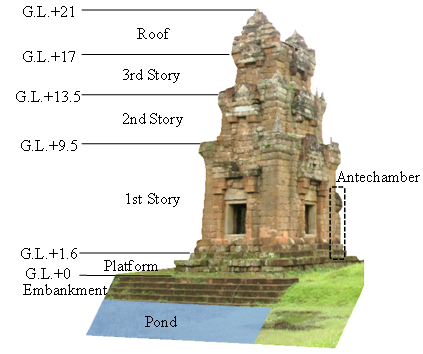 | Figure 3. Outward appearance of Prasat Suor Prat N1 Tower (after restoration) |
The damages before the restoration are summarized as follows (see Fig. 1) (JSA [1], Iwasaki et al. [7]).• The tower inclined 4.96%/2.84º toward northwest (4.60%/2.63º toward north from west side).• Some blocks fell down due to the inclination of the tower.• Some critical joint openings were observed in the upper and lower platform and along the wall of the tower (especially, around the windows).Above mentioned damages may be caused by uneven settlement of the foundation ground. Therefore, it is necessary to consider the interaction between masonry building and foundation ground for the stability analysis using accurate stress redistribution of masonry blocks. The following issues may be related to the uneven settlement of foundation ground.• A sliding toward the bathing pond by cutting slope and uneven soil pressure (Fig. 4).• Stress concentration due to weathered laterite blocks and/or changes of the stress transmission paths.• Changing mechanical properties of foundation ground due to rain water infiltration and wet-dry-cycle.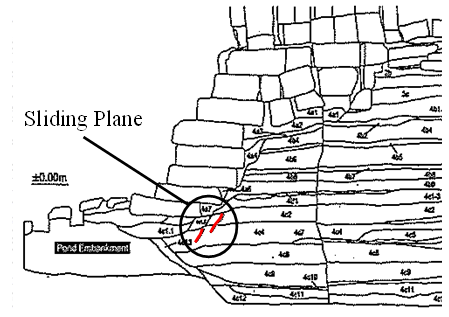 | Figure 4. Trench cross section inside the rammed earth and the observed shear plane |
Since the N1 Tower is a typical building deteriorated due to the deformation of the rammed earth, it would be an appropriate example to observe the influence of the compaction quality of the rammed earth.
5. Stability analysis of Prasat Suor Prat N1 Tower
5.1. Outline of the Simulation
Fig. 5 shows the numerical model of Prasat Suor Prat N1 Tower (in 2-D, plane strain condition), which was created based on the sketch from west side view after restoration. The masonry blocks, which may possibly collapse during the simulations, were modelled by DDA and the foundation ground which consists of rammed earth and natural ground was modelled by NMM. This enabled to focus on the large displacement of the blocks (include joint openings) and the local distribution of stress/strain in the foundation ground simultaneously. The displacements in both normal and horizontal directions, and only horizontal direction were fixed along the bottom and side edges of the analytical domain, respectively. All masonry blocks were modelled as linear elastic body, and the subloading modified Cam-clay model (Hashiguchi et al. [6]) was applied to the foundation ground (for both natural ground and compacted soil layer). The material properties used for the simulations are summarized in Table 1. These values except the critical state stress ratio M of the natural ground were determined from laboratory tests for soil samples obtained from the site, and M of the natural ground was set assuming that the internal friction angle 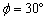 . Table 2 shows the joint properties used in the simulations.
. Table 2 shows the joint properties used in the simulations.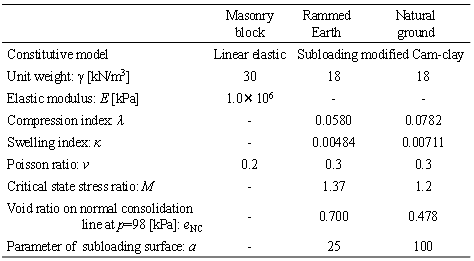 | Table 1. Material properties |
Table 2. Joint properties
 |
| |
|
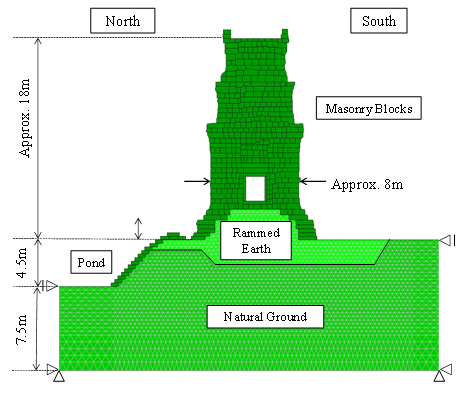 | Figure 5. Analytical domain (2D, plane strain condition) |
Initial stress of whole ground was obtained from the self-weight analysis. Initial void ratio of the natural ground was set assuming the normally consolidated state. In order to investigate the effect of compaction quality, two different initial void ratios of the rammed earth were set (called Case A and B, see Table 3). In Case A, the rammed earth is assumed to be compacted with optimum water content and the value of the initial void ratio is based on the compaction test, and Case B is a looser compaction case.Table 3. Simulation cases
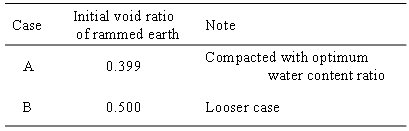 |
| |
|
During the simulations, only the self-weight of the masonry blocks was applied, and the simulations were continued until the displacements of the blocks became stable.
5.2. Simulation Results
Firstly, the distributions of the vertical displacement at the end of the simulation in two cases are shown in Fig 6. These figures obviously show the following facts.• Northern side of the tower settled larger in both cases as observed before the restoration.• The settlement of Case B (looser case) is larger.The differential settlement between the north and south sides of the tower, and the northward inclination of the tower for each case are summarized in Table 4. These values were calculated from the coordinates of block (N) and (S) in Fig. 6 at the end of the simulation. In addition to the settlement itself, both the differential settlement and the inclination of the tower became larger in Case B.Table 4. Differential settlement and northward inclination of the tower
 |
| |
|
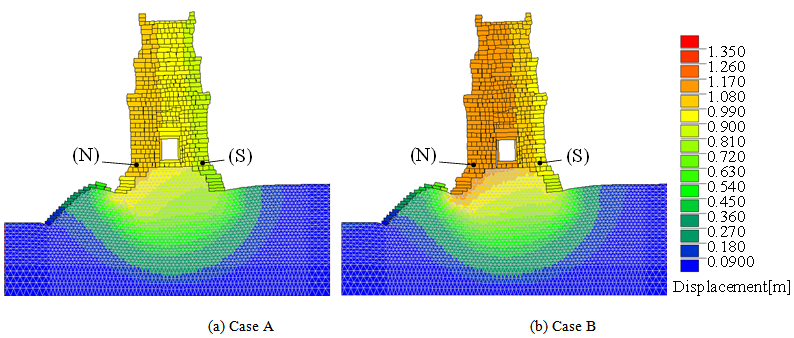 | Figure 6. Distribution of the vertical displacement at the end of the simulation |
These results imply that the compaction quality of the rammed earth has much influence on the stability of the structure. This means that controlling the compaction quality of the rammed earth during the restoration process is significantly important for the permanent conservation of the Angkor monuments.
6. Conclusions
In this paper, NMM-DDA with the subloading modified Cam-clay model was applied to the stability analyses of Prasat Suor Prat N1 Tower in Angkor. The simulations were carried out in two cases with different initial density (void ratio) of the rammed earth. From the simulation results, the influence of construction quality of the rammed earth on the stability of the structure was investigated. The findings obtained from this study are summarized as follows.• Inadequate compaction of rammed earth causes the increase of the differential settlement and the inclination of the tower.• Controlling the compaction quality of the rammed earth is significantly important for the permanent conservation of the Angkor monuments.In the future, to apply the NMM-DDA to the design process of the restoration method for Angkor monuments, following subjects should be researched.• Accumulating the data of the mechanical properties of the in-situ soil.• Coupled stress-flow behavior in the foundation ground such as rainwater infiltration and its effect of mechanical behavior of the tower.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI, Grant-in-Aid for JSPS Fellows, 26-77. The authors are really grateful to Dr. Shigeru Miki, Kiso-Jiban Consultants Co., Ltd, Dr. Takeshi Sasaki, Suncoh Consultants Co., Ltd., and Dr. Mitsuharu Fukuda, Taisei Geo Tech, for their valuable comments and suggestions.
References
| [1] | Japanese Government Team for Safeguarding Angkor (JSA). Report on the conservation and restoration work of the Prasat Suor Prat Tower. OGAWAINSATSU Co., Ltd.. 2005. |
| [2] | S. Miki, T. Sasaki, T. Koyama, S. Nishiyama & Y. Ohnishi. Development of coupled Discontinuous Deformation Analysis and Numerical Manifold Method (NMM-DDA). Int. J. Computational Methods, 2010, 7(1): 1-20. |
| [3] | R. Hashimoto, T. Koyama, M. Kikumoto, S. Yamada, M. Araya, Y. Iwasaki & Y. Ohnishi. Stability analysis of masonry structures in Angkor Thom, Cambodia using elasto-plastic NMM-DDA with subloading Cam-clay model. In: Proc. of the 47th US Rock Mechanics/Geomechanics Symposium. 2013, paper No.13-362 (CD-ROM). |
| [4] | G.H. Shi. Manifold Method of material analysis. Trans. the 9th Army Conf. on Applied Mathematics and Computing, 1991, 92(1). U.S. Army Research Office. |
| [5] | G.H. Shi & R.E. Goodman. Two Dimensional Discontinuous Deformation Analysis. International Journal for Numerical and Analytical Methods in Geomechanics 9. 1985, pp. 541-556. |
| [6] | K. Hashiguchi & M. Ueno. Elastoplastic constitutive laws of granular material. Constitutive Equations of Soils, In: S. Murayama and A.N. Schofield (eds.). Proc. of 9th Int. Conf. Soil Mech. Found. Engrg., Spec. Ses. 9, Tokyo. JSSMFE. 1977, pp. 73-82. |
| [7] | Y. Iwasaki, M. Fukuda, K. Nakagawa, A. Akazawa, I. Shimoda & T. Nakagawa. Geotechnical Aspects of the N1 Tower, Prasat Suor Prat, Angkor Thom, Cambodia. Advanced Materials Research, 2010, Vol. 133-134: 113-118. |


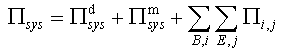
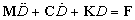
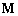 is the mass matrix,
is the mass matrix, 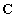 is the viscosity matrix,
is the viscosity matrix, 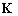 is the stiffness matrix, and
is the stiffness matrix, and 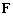 is the external force vector.
is the external force vector. 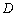 ,
, 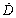 and
and 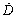 are the displacement, velocity, and acceleration of DDA blocks and the nodes of NMM elements, respectively. In the process of deriving the stationary condition, the first and second terms of the right side in Eq. (1) are minimized in terms of the displacement variables of the DDA blocks (
are the displacement, velocity, and acceleration of DDA blocks and the nodes of NMM elements, respectively. In the process of deriving the stationary condition, the first and second terms of the right side in Eq. (1) are minimized in terms of the displacement variables of the DDA blocks (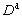 ) and the NMM elements (
) and the NMM elements (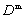 ), respectively same as DDA and NMM alone. The third term, specific to NMM-DDA, is minimized in terms of both
), respectively same as DDA and NMM alone. The third term, specific to NMM-DDA, is minimized in terms of both 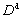 and
and 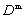 . Consequently, in the formulation of NMM-DDA, only defining the potential energy for the contacts between DDA blocks and NMM elements is newly required. The detailed explanations for the theory of NMM-DDA and derivation of the contact sub-matrixes can be seen in the references (Miki et al. [2]). The original NMM-DDA code treats only linear elastic material, however, elasto-plastic NMM-DDA code was also developed by Hashimoto et al. [3].
. Consequently, in the formulation of NMM-DDA, only defining the potential energy for the contacts between DDA blocks and NMM elements is newly required. The detailed explanations for the theory of NMM-DDA and derivation of the contact sub-matrixes can be seen in the references (Miki et al. [2]). The original NMM-DDA code treats only linear elastic material, however, elasto-plastic NMM-DDA code was also developed by Hashimoto et al. [3].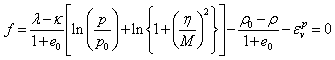
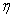 is the stress ratio (=q/p). ρ is the parameter of overconsolidation expressed as follows;
is the stress ratio (=q/p). ρ is the parameter of overconsolidation expressed as follows;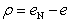
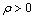 , and in normally consolidated state,
, and in normally consolidated state, 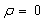 .
. 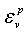 is the plastic volumetric strain. Defining the evolution rule of
is the plastic volumetric strain. Defining the evolution rule of 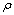 as
as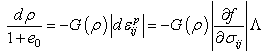
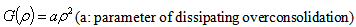


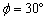 . Table 2 shows the joint properties used in the simulations.
. Table 2 shows the joint properties used in the simulations.


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

