-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Ecosystem
p-ISSN: 2165-8889 e-ISSN: 2165-8919
2015; 5(3A): 1-5
doi:10.5923/c.ije.201501.01
Solubility of Fluorine and Chlorine Containing Gases and Other Gases in Water at Ordinary Temperature
Debaprasad Panda, Indranil Saha
Dept. of Chemistry, Sripat Singh College, Jiaganj, Murshidabad, W.B, India
Correspondence to: Debaprasad Panda, Dept. of Chemistry, Sripat Singh College, Jiaganj, Murshidabad, W.B, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Gas solubilities are used in a wide variety of application from industrial to biochemical to oceanographic to environmental pollution control to the study of the properties of solution. Chlorine and Fluorine containing gases also destroy the ozone layer and it becomes the subject of extensive laboratory investigation especially after the discovery of the Antarctic ozone hole. Due to known atmospheric history and chemical stability of fluorine containing gases, they are become valuable to oceanographer as chemical tracers of ocean mixing and circulation pathways. To realize the distribution of fluorine containing gases and other in ocean and study the exchange of gases between natural water and the atmosphere, it is necessary to know their solubility and its mechanism. In this case predicted solubility in term of Henry’s law constant using scale particle theory (SPT) of methyl fluoride, methyl Chloride, carbon monoxide and nitric oxide and nitrous oxide in water. The aim of this research is to Ø to understand the solubility of gases from thermodynamics and statistical mechanical first principle. Ø to understand interaction of gases with water molecules. Ø to study the equilibrium solubility of sparingly soluble gases in liquids equilibrium solubility of sparingly soluble gases in water.
Keywords: Solubility, Water, Fluorine, Scale particle theory, Gases
Cite this paper: Debaprasad Panda, Indranil Saha, Solubility of Fluorine and Chlorine Containing Gases and Other Gases in Water at Ordinary Temperature, International Journal of Ecosystem, Vol. 5 No. 3A, 2015, pp. 1-5. doi: 10.5923/c.ije.201501.01.
1. Introduction
- Of the three general state of matter, the liquid is most complex. It has neither the extreme order of the solid nor there extreme disorder of the gaseous state. The liquid state remains the one which is least understood and most difficulty to model in a satisfactory manner. The liquid, most difficult of all to model is our commonest one, water. A model is a difficult task still is to be developed to account for all types of aqueous solutions. A vast number of research articles have been devoted to the structure of water and aqueous solution. it will be an impossible task to mention even a small fraction of these [1, 2]. However, a central work landmark in this respect was the fundamental work of Bernal and Flower [3] followed by Feank [4] –water contains ‘cluster’ of hydrogen bond molecules, code name ‘iceberg’. Nemethy and Schrage [5] structure is temporary and chaining ‘flickering cluster’. Ben-Naim [6] –there is a dynamic equilibrium between some bonded and non-bonded water molecules, with hydrophobic interactions between solute particles being important. Bernal [7] also favored continuum theories rather than mixture theories of water structure based on the concept of strain and bent hydrogen bonds.Following a critical survey of the vast recent literature Schmid [8] stated that nature of liquid water can be understood in terms of a competition between H-bond (coulomb) and dispersion (van der Waals) forces. Since the bonding characteristics in crystalline face carry over to the liquid state, any molecular dynamics model of the liquid would have first to reproduce well the ice polymorph structures under appropriate thermodynamic condition. Once it has been recognized that water is a structure liquid, the immediate question that arises is how this structure changes when we add various solutes in water. These are, of course, a different meaning, view and definition of the concept of the structure of water [9, 10].Solubility is an old subject, although most of the early interest was in the solubility of solids in water, which is still an important area of research and applications. Early quantitative measurements of the solubility of gases, a more difficult measurement were made by William Henry, as well as by Cavendish, Priestley and others. Henry studied the pressure and temperature dependency of air, hydrogen, nitrogen, oxygen and other gases in water. He discovered, among other things that oxygen is more soluble than nitrogen in water. This is an early example of the principle that is the basis of preferential extraction of one gas from a mixture of gases by use of the solvent.For calculating the solubility of gases in water, Swope and Andersen [11] developed a coupling parameter method for calculating the chemical potential of a solute in a solution using molecular dynamics calculations and applied it to the study of inert gases in water. The calculation used a modified version of the revised central force model for the water-water interaction and a Lennard –Jones interaction between the solute atom and the oxygen atom of water molecule. The revised central force model and it’s modification given by Swope and Andersen is not a perfect model of water. In addition, they omit the long ranged dipole-dipole interactions. The real repulsive interactions are presumable also dependent on the orientation of water molecule and not just the distance of the atom from oxygen.The statistical mechanical theory of fluids employing distance scaling as a coupling procedure and hence called scaled particle theory (SPT) has been developed by Reiss et al [12-14]. Pieroitti [15] developed a theory using the SPT for prediction the solubility of gases in water. The most surprising aspect of the theory is that it appears to predict the thermodynamic properties (Gibbs free energy, entropies, enthalpies, molar heat capacities etc) of gases dissolve in water successfully. The abnormal thermodynamic properties of aqueous solution are discussed in light of the enthalpy and entropy of cavity formation. Basic to the theory is the use of term derived by Reiss et al for the calculation of reversible work of making a cavity in a hard sphere solvent. The prescription used for the gas dissolution process in water is a very simple one. The gas solute is discharged to a hard sphere, as a hard sphere makes a cavity in the real solvent. Finally the solute is recharged and allowed to interact with solvent molecule. Pieroitti assumes equivalency of this of this reversible work required for cavity formation and cavity formation energy (CFE). Pierotti [16] compare to reversible work require producing cavity in a fluid and the same require for macroscopic cavity formation in classical thermodynamics. This comparative calculation can be avoided as Matyushov and Ladanyi [17] they directly calculated the cavity formation energy from the exact geothermal relation valid for sphere fluid. In the present communication this cavity formation energy expression is used to calculate the solubility of gases in water.
2. Methodology
- The equation of solubilityThe Henry’s law constant (solubility) and thermodynamic functions of solution pertaining to the solution process calculated in usual manner utilizing scale particle theory (SPT) formalism, considering dissolution of gas in a liquid takes place through two steps:a) First, the creation of a cavity in the solvent of suitable size to accommodate the solute molecules, its diameter exactly the hard sphere diameter of the solute gas. This is referred to as a cavity formation process. The free energy associate with this process is called cavity formation energy (CFE /βμcav).b) The second step involved introduction of solute molecule in to the cavity of the solvent and hence interaction between solute and solvent occurs according to some potential law. The energy a associated with this process is called Gibbs free energy of interaction.The solubility of gas in liquid is described by Henry's law constant (KH) as
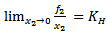 | (1) |
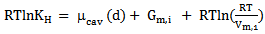 | (2) |
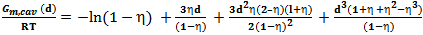 | (3) |
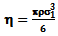 is the "compactness factor" of solvent. The number density of solvent is define by ρ = NA/Vm,1, NA is a Avogadro’s number and Vm,1 = density/molecular weight, σ1 hard sphere diameter of the solvent and d = σ2/σ1, σ2 is hard sphere diameter of the solute gases. The last term of the above equation is related to hydrostatic pressure for gas solubility in incompressible liquids at 1 atmosphere pressure, it can be neglected. Computation of Interaction energy of solute with mixed solventsThis term represent the partial molar free energy of interaction when a solute molecule introduce into a solvent cavity. This consists of three terms; a dispersion energy term, an inductive energy terms and dipole-dipole interaction energy term. Solubility of polar gases in water was calculated by following expression
is the "compactness factor" of solvent. The number density of solvent is define by ρ = NA/Vm,1, NA is a Avogadro’s number and Vm,1 = density/molecular weight, σ1 hard sphere diameter of the solvent and d = σ2/σ1, σ2 is hard sphere diameter of the solute gases. The last term of the above equation is related to hydrostatic pressure for gas solubility in incompressible liquids at 1 atmosphere pressure, it can be neglected. Computation of Interaction energy of solute with mixed solventsThis term represent the partial molar free energy of interaction when a solute molecule introduce into a solvent cavity. This consists of three terms; a dispersion energy term, an inductive energy terms and dipole-dipole interaction energy term. Solubility of polar gases in water was calculated by following expression 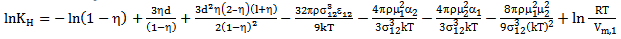 | (4) |
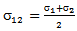 and
and 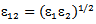 where ε1 and ε2 are Lennard-Jones (6-12) parameter for solvent solute gas respectively and μ1is the dipole moment of the solvent.
where ε1 and ε2 are Lennard-Jones (6-12) parameter for solvent solute gas respectively and μ1is the dipole moment of the solvent.3. Results and Discussion
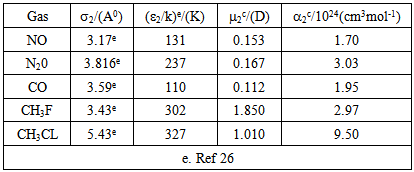
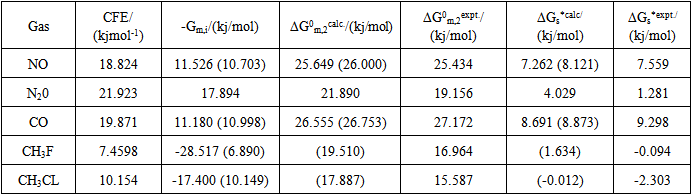
- The cavity formation energy of water is calculated by means of equation (3) at 298.15K given in the table1. The cavity formation energy plotted against ratio of hard sphere diameter of solute (gas) to water which shown in Figure 1. The necessary physical parameters of water are given in the table 2. From this curve we see that the cavity formation energy increases monotonically with rise of ratio of hard sphere diameter of solute gases to water. Since latter decreases with decrease of hard sphere diameter of solute gases, so we concludes that water easily form cavity when a small solute molecule across it than larger one.
|
|
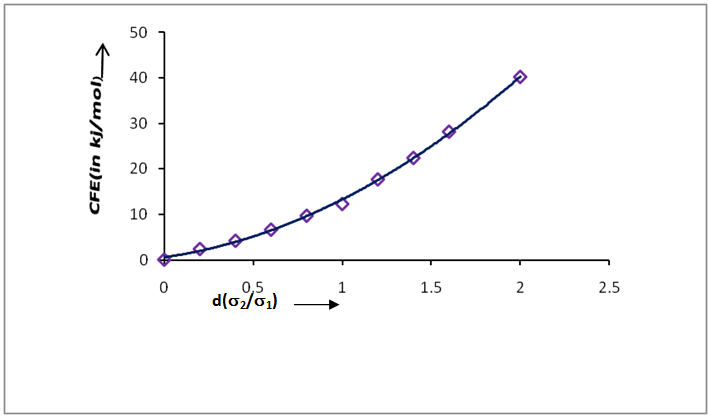 | Figure 1. Cavity formation energy, CFE(kj/mol) of water with ratio of hard sphere diameter at 298.15k |
|
|
|
4. Conclusions
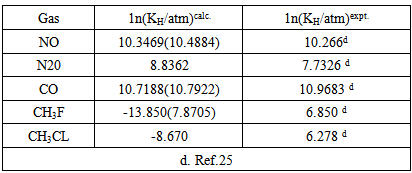
- There is some discrepancy between calculated experimental Henry’s law constant. But the discrepancy for polar gases especially methyl fluoride and methyl chloride are very large. The results in Table 4 within the first backed that if these solutes are consider non-polar(only dispersion force contribution to interaction energy) then calculated and experimental logarithm of Henry’s law constant will be closed to each other. It is as if the collective effect of solvent electric field on the solute particle. In, addition lnKH in water depends upon two factors: one is cavity formation energy and other is interaction energy. The calculated cavity term extremely sensitive to the choice of the diameter of the water since hard sphere diameter of solvent water (σ1) is raised to the sixth power in the calculations. The value of hard sphere diameter of solvent and solute available in the literature may be calculated from the surface tension viscosity, second virial coefficient, heat of vaporization, molecular dynamic simulation and gas solubility etc. The results obtained from different experiment are not unique. As example hard sphere diameter in 0A of water are 2.77(ref16), 2.76, 2.75(ref 15) 2.86(ref 29) 2.89(ref 30) 2.56 and 2.922 ref(31) 2.65(ref 32) so exact choice of this parameter is difficult and it is possible that values used were in error. The differences between experimental and calculated values arise from this choice. Moreover the solute and solvent interaction energy is sensitive to the values of ε/k the Lennard-Jones parameter of the solute and solvent. The value of this parameter is not also unique as for example argon ε/k range from 117 to 125. So proper choice of ε/k and σ gibes the exact experimental result s as expected. In conclusion we can say that however, present statistical mechanical approach, in spite of the rigid hard sphere model employed, is able to reproduce rather successfully to predict solubility of gases in water. If we could choose proper value of molecular parameters then it can give exact experimental results as expected.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML